莱斯信道下低精度ADC去蜂窝大规模MIMO系统的性能分析
闫秋娜 金思年,2 岳殿武,2 鞠默然
(1.大连海事大学信息科学技术学院,辽宁大连 116026;2.东南大学毫米波国家重点实验室,江苏南京 210096)
1 引言
近年来,随着移动通信产业的飞速发展,人们对于数据流量方面的需求与日俱增。为了满足各种多样化的通信需求,对蜂窝网络架构进行彻底变革的去蜂窝大规模多输入多输出(Multiple Input Multiple Output,MIMO)系统逐渐走进了人们的视野,并成为了B5G(Beyond 5G)和6G 时代应该密切关注的核心技术之一[1-6]。去蜂窝大规模MIMO 系统的概念最早由Ngo Hien Quoc 等学者于2017 年首次提出[1],该系统以分布式大规模MIMO 为基础,破除了小区边界的划分,即在一片广阔的区域内,同时分布着大量的接入点(Access Point,AP)和用户,不同的AP 通过回程链路与中央处理单元(Central Processing Unit,CPU)相连接,并在相同的时频资源下,听从CPU 的指令向所有的用户提供服务。由于去蜂窝大规模MIMO 系统极大地降低了用户与AP之间的距离,因此具有较强的空间宏分集增益和抵抗路径损耗的能力,并可以大幅度地提升边缘用户的服务质量[2]。
然而,去蜂窝大规模MIMO 系统通常需要部署大量的AP 和用户,当AP 和用户配置了全精度的模数转换器(Analog-to-Digital Converters,ADCs)对接收信息进行量化处理时,势必会带来高昂的硬件成本和巨额的能量消耗。为了应对该问题,通过在AP和用户处配置低精度的ADC 进行量化处理无疑是一种比较直接的解决方案。因此,针对配置有低精度ADC 的去蜂窝大规模MIMO 系统研究是十分具有理论价值和实际意义的[7-10]。基于此,文献[7]研究了当所有的AP 和用户都配置了低精度的ADC时,瑞利衰落信道下的下行去蜂窝大规模MIMO 系统可达速率,并提出了一种能够最大化系统总速率的量化比特数分配方案,仿真结果验证了该分配方案的有效性。相较瑞利衰落信道,莱斯衰落信道作为一种更加符合未来通信场景的信道环境理应受到重视。这是因为在未来诸多的通信场景中,为了应对日益紧张的频谱资源,去蜂窝大规模MIMO系统很可能会运行在毫米波频段。由于毫米波具有波长短和方向性强的特点,这会导致视距分量在整个信道中占据主导地位,所以对莱斯衰落信道环境下的系统性能分析是十分有必要的[11]。因此,文献[8]研究了当AP 端配置了低精度的ADC而用户端配置了全精度的ADC 时,莱斯衰落信道下的下行去蜂窝大规模MIMO 系统性能,并且提出了一种基于max-min 准则的加权功率控制算法。仿真结果表明,所提算法能够在提升高优先级用户服务质量(Quality-of-Service,QoS)的同时,有效地保证低优先级用户的QoS。此外,文献[9]研究了当AP 端配置了混合ADC 而用户端配置了全精度ADC 时,莱斯衰落信道下的上行去蜂窝大规模MIMO 系统性能,发现了相较全部配置了全精度ADC 的系统,混合ADC 架构可以更好地发挥系统的能量效率。
不过,针对莱斯衰落信道下的去蜂窝大规模MIMO 系统,文献[8]和[9]只考虑了在AP 端配置有低精度ADC 而用户端配置了全精度ADC 时的系统性能。然而,在未来的物联网场景中,受到硬件成本的限制,不仅AP 端会使用到低精度的ADC,用户端同样也不可避免的会配置到低精度ADC。但是,关于这一方面的研究工作,目前仍未被开展。基于此,当AP 和用户端都配置了低精度的ADC 时,本文将针对莱斯衰落信道下的下行去蜂窝大规模MIMO系统展开研究。首先,当AP端通过最小均方误差法(Minimum Mean Squared Error,MMSE)获取到来自用户端的信道状态信息(Channel State Information,CSI)时,推导了该系统使用共轭转置(Conjugate Beamforming,CB)预编码的可达速率闭合表达式。然后,从提升系统整体性能的角度出发,提出了一种基于连续凸逼近(Successive Convex Approximation,SCA)准则的功率控制算法,并且所提算法能够在保证每个用户的最低QoS 和满足每个AP 的发送功率不超过既定功率的前提下,最大化系统的总速率。最后,通过数值仿真也验证了所提算法的有效性。
本文使用的符号:CM×N表示M×N的复空间;(·)*、(·)T和(·)H分别表示共轭、转置和共轭转置;IN和diag{x1,…,xN}分别表示N×N的单位矩阵和对角元素为{x1,…,xN}的对角矩阵;[A]mn表示矩阵A的第m行n列元素;E{·}表示期望运算;δ(m,n)表示狄拉克δ 函数,即当m=n时,δ(m,n)=1,当m≠n时,δ(m,n)=0;z~CN(x,y)或z~N(x,y)分别表示均值为x且方差为y的循环对称复高斯变量或高斯变量。
2 去蜂窝大规模MIMO系统模型
如图1 所示,本文主要考虑了一个莱斯衰落信道下的去蜂窝大规模MIMO 系统,其中M个单天线的AP与N(M>N)个单天线的用户随机地分布在一片广阔的服务区内,并且所有的AP 通过回程链路与CPU 相连接,并向所有的用户提供服务。另外,为了有效地降低全精度ADC 量化器所带来的高昂硬件成本和巨额能量消耗,本文假定在AP 和用户处配置低精度的ADC 量化器来对接收数据进行量化处理。为了充分地利用信道互易性的特点,本文还假定该系统工作在时分双工模式下,并将研究重心聚焦在下行信号传输阶段。因而,对本文而言,只需要关注上行链路的导频训练模型和下行链路的数据传输模型即可。
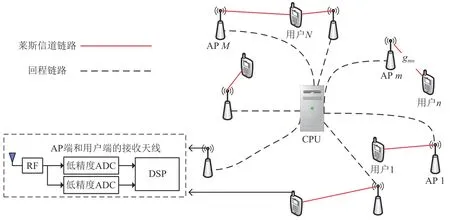
图1 莱斯信道下基于低精度ADC的去蜂窝大规模MIMO系统Fig.1 Cell-free massive MIMO system with low-resolution ADCs under Rician fading channels
我们用gmn表示第m个AP 与第n个用户之间的信道系数,则信道系数gmn可以建模为[8]:

2.1 上行链路的导频训练模型
令相关间隔的长度为T,并令每个相关间隔中导频训练所占用的时间为τp(τp≥N)。在上行导频训练阶段,第n个用户可以向所有的AP发送上行导频序列fn∈,并且假定不同用户间发送的导频序列是相互正交的,即=0(n≠n1)。由于AP装配了低精度的ADC,因此它的量化误差会受到接收信号强度的影响。为了探究低精度ADC 对于系统性能的影响,本文考虑使用加性量化噪声模型[12-13](Additive Quantization Noise Model,AQNM)对量化过程进行建模,则第m个AP 接收到的上行导频信息可以重新表示为
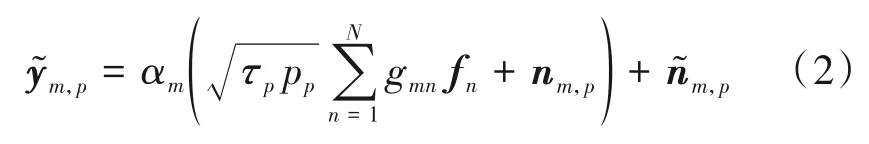
其中pp表示上行导频信号的归一化信噪比(Signal Noise Ratio,SNR),nm,p~表示第m个AP接收到的加性高斯白噪声,αm表示第m个AP 处的ADC 精度对于接收信号幅度的影响,并且这个精度与第m个AP使用的量化比特数ρm有关[12-13]。当量化比特数ρm=1,2,3,4,5 时,αm可以被精确地给定为αm=0.6366,0.8825,0.96546,0.990503,0.997501;当ρm>5 时,αm与ρm之间满足αm=1-的近似关系。表示与接收信号ym,p无关的加性量化噪声。根据文献[8],的协方差可以表示为。
为了使第m个AP 可以获取到来自第n个用户的CSI,我们可以将相乘,既可以得到
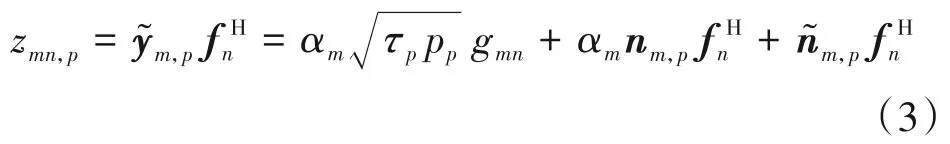
根据文献[8],可知AP 能够获取到来自不同用户的视距分量信息和大尺度衰落系数。因此,在信道估计阶段,系统可以消除视距分量的影响,即式(3)可以重新表示为

2.2 下行链路的数据传输模型
当AP 获取到来自用户的CSI 后,本文将采用CB 的方式对下行发送信号进行预编码处理。之所以选择CB 方案,是因为每个AP 只需要用到本地估计的CSI,而不需要与其他AP 或CPU 进行即时CSI交换。当AP 的数量很大时,这种方案可以有效地降低处理复杂度。因此,第m个AP 的发送信号可以表示为

其中xn表示发往第n个用户的数据信号,满足E{|xn|2}=1 的条件;pd表示下行发送数据信号的归一化SNR;ηmn表示功率控制系数。通过调节ηmn,可以使每个AP 满足E{|sm|2}≤pd的功率约束条件,即
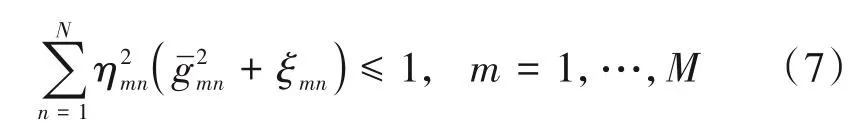
根据式(6),当所有的AP 发送完下行数据信号后,第n个用户的接收信号可以表示为

其中wn~CN(0,1)表示第n个用户接收到的加性高斯白噪声。由于用户端也使用了低精度的ADC,因此第n个用户经过量化处理后的接收信号可以表示为
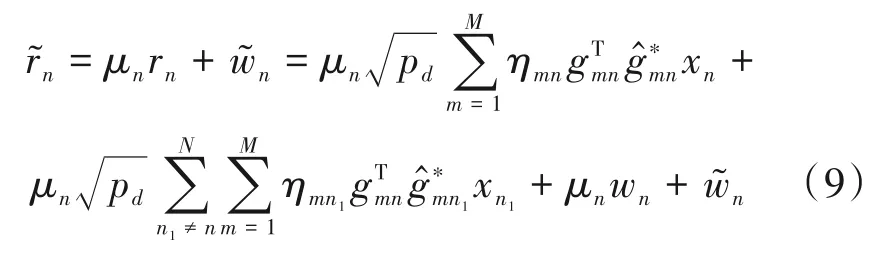
其中μn表示第n个用户的ADC 精度对于接收信号幅度的影响,这个精度与第n个用户使用的量化比特数σn有关,具体的μn和σn的对应关系可以参考第m个AP 的ADC 精度αm和量化比特数ρm之间的数值对应关系,在此就不再重复进行赘述。表示与接收信号rn不相关的加性量化噪声,并且它的协方差可以表示为
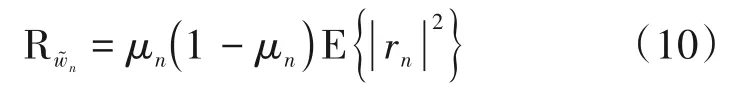
2.3 下行可达速率
根据式(9),我们可以将第n个用户的接收信号重新表示成如下形式


我们将式(11)中第二项、第三项、第四项和第五项的总和称为“有效噪声”,并且有效噪声与第一项中的有用信号是不相关的。根据Use-and-thenforget 理论,我们可以获得第n个用户的可达速率表达式为[14]

定理1:根据式(12),去蜂窝大规模MIMO 系统中第n个用户的可达速率闭合表达式为
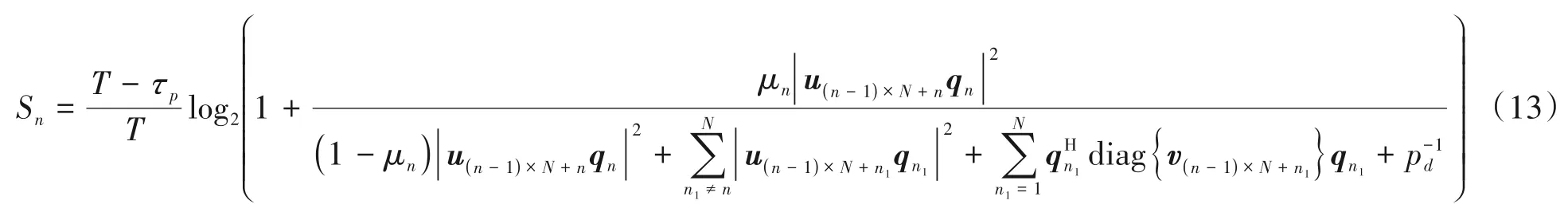


推论1:根据式(13),当所有的AP 与用户间都处于只有视距分量的信道环境下,即κmn→∞,m=1,…,M和n=1,…,N时,第n个用户的可达速率闭合表达式将趋近于

3 功率控制算法
针对现代通信系统,每个用户的服务质量和系统的总速率是评价一个通信系统好坏的重要性能指标。为了提升系统的整体速率性能,本节想要设计一种可以在保证每个AP 的发送功率受限于pd且每个用户的可达速率性能不小于目标可达速率性能Sˉ的前提下,通过调节不同用户的功率控制系数([Q]mn=ηmn)来最大化系统总速率的功率控制算法。根据定理1给出的用户可达速率闭合表达式和上述限制条件,最大化系统总速率的优化问题可以归纳成如下形式:
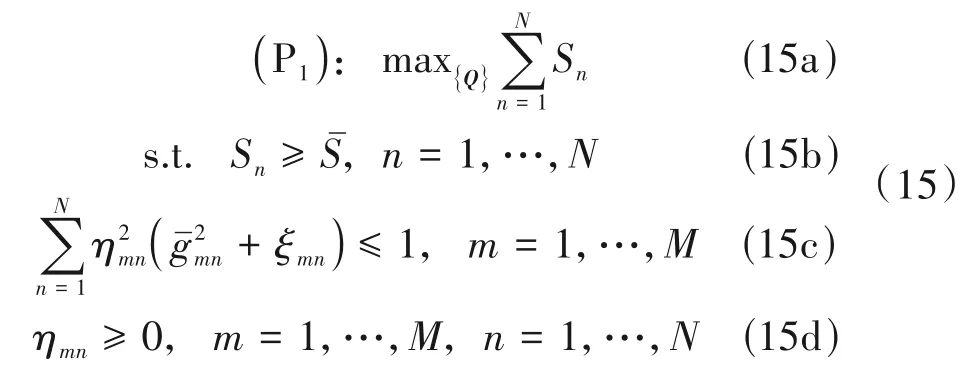
通过观察,我们可以发现优化问题P1中的目标函数是非凸的;约束条件(15b)可以等价成式(16)中的二阶锥形式,因此式(15b)转换成了式(16)中的凸约束条件;式(15c)和(15d)都为凸约束条件。

由于优化问题P1中的目标函数是非凸的,所以该优化问题没办法通过凸优化求解器直接获取全局最优解。因此,为了顺利解决上述优化问题,我们可以采用SCA 的思想,将非凸优化问题P1近似等价成优化问题P2的形式,并且文献[15]证明了经过SCA方法求得的次优解是收敛的。如果我们能够顺利地解决优化问题P2,则可以得到一个能够解决优化问题P1的次优化解,并且这个次优化解接近于全局最优解。下面,我们给出了优化问题P2的具体形式为:
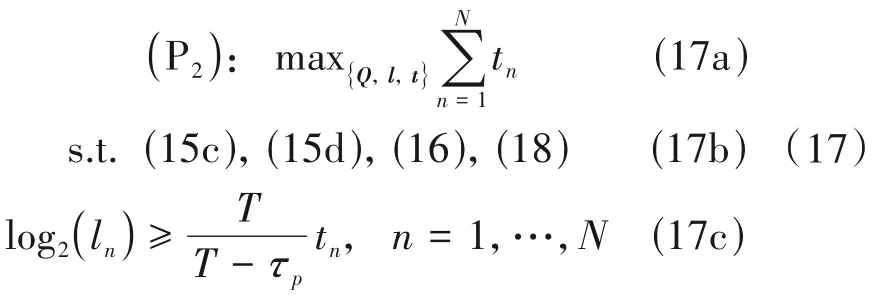
其中l=[l1,…,lN]和t=[t1,…,tN]。

通过观察,我们可以发现优化问题P2中的目标函数(17a)是凸的,但是约束条件(18)却不是凸的。因此,为了解决优化问题P2,我们需要将式(18)转换为凸函数的形式。首先,式(18)可以等价成:

然后,根据文献[16]中的SCA 方法,我们可以使用式(22)中的一阶泰勒展开式来近似式(20)。因此,当n=1,…,N时,式(19)可以重新表示成如下的形式:
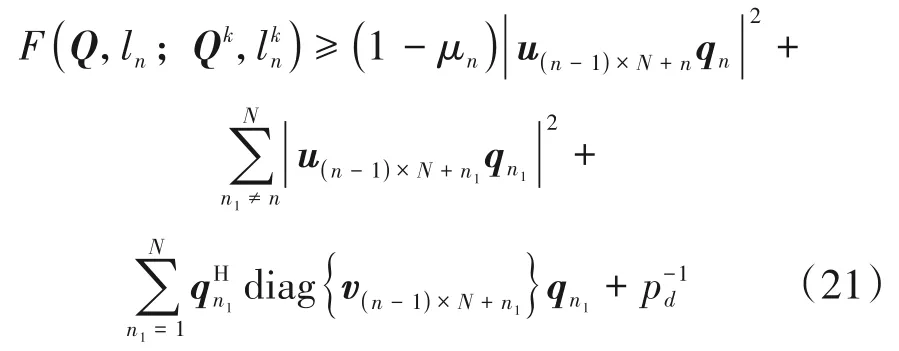
其中
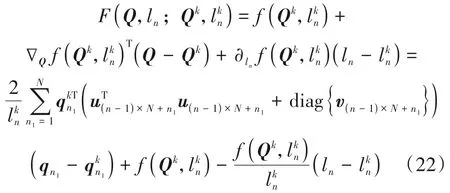
其中Qk和分别表示Q和ln经过k次SCA 处理后的迭代值。基于此,式(18)已经通过式(21)成功地转换成了二阶锥形式的约束条件。另外,通过观察优化问题P2,我们可以发现约束条件(17c)是凸的。不过,现存的求解器在解决这种形式的凸约束条件时,会先将其转换成大量的二阶锥和指数锥形式的约束条件,然后再进行求解,这显然带来了巨大的计算复杂度。因此,为了降低求解复杂度,我们可以根据SCA 的思想,并利用不等式ln(x)≥1-x-1的性质,将式(17c)转换成如下具有二阶锥形式的约束条件[16]:
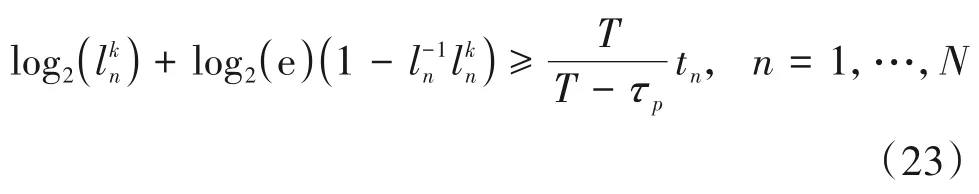
根据式(21)和式(23),在第k次迭代时,我们可以将优化问题P2表示成如下形式的二阶锥规划问题:

当通过使用现代的凸优化求解器(如Gurobi或者Mosek)解决二阶锥规划问题(P2,k)后,我们就可以得到解决优化问题P1的次优解,并且具体的求解算法给定在下面的表1中。

表1 功率控制算法Tab.1 Power control algorithm
4 仿真结果
首先,我们给定莱斯信道下基于低精度ADC的去蜂窝大规模MIMO 系统的仿真环境:AP 的数量M;用户的数量N;相干时间长度T=200;上行导频的长度τp=N;上行导频信号和下行数据信号的发送功率分别为=200 mw;噪声的功率N0=-94 dBm;上行导频信号和下行数据信号的归一化信噪比分别为。ρm和σn分别表示第m个AP 和第n个用户处使用到的量化比特数;在不失一般性的情况下,对于m=1,…,M和n=1,…,N,给定ρm=ρ和σn=σ。我们假定所有的AP 和用户随机地分布在一片1 km×1 km 的正方形区域内,并且第m个AP 与第n个用户间的距离为dmn。然后,根据文献[17],大尺度衰落系数(dB)定义为γmn=-30.18-26 lg10(dmn)+Fmn,其中Fmn=表示阴影衰落,系数am~和bn~是相互独立的,并且本文假定δsf=0.5和σsf=8。最后,根据文献[17],莱斯K-因子给定为κmn=。
在N=10 和不使用功率控制算法的情况下,图2(a)比较了当AP 和用户端使用不同数量的量化比特数对接收信号进行量化处理时,用户的总速率与AP 数量之间的关系,其中蒙特卡洛仿真曲线和理论闭合表达式可以通过将式(12)和式(13)分别代入S=来获得。此外,需要说明的是,当系统不使用功率控制算法时,为了满足式(7)中的功率约束条件,我们可以设定不同用户的功率控制系数为ηmn=。根据图2(a),我们可以发现理论推导的闭合表达式与仿真得到的数值十分吻合,这验证了理论推导的正确性,也为我们更好地了解不同参数对于系统速率性能的影响提供了帮助。然后,我们可以发现相较AP 端使用大数量的量化比特数处理接收信号的情况,用户端使用大数量的量化比特数可以更好地提升系统性能,这表明了用户端ADC 量化器的精度对于系统性能的影响更为显著。另外,当所有的AP 和用户使用相同的量化比特数(ρ=σ)处理接收信号且M=100 时,图2(b)比较了用户的总速率与ADC 的量化比特数之间的关系。通过观察图2(b),我们可以发现随着AP 和用户端使用的量化比特数量不断增加,用户的总速率也随之不断地增加,并且当量化比特数大于4 bit 后,用户的总速率逐渐趋近于一个定值。这一结果也表明了在AP 和用户端使用4 bit的量化器是一种兼顾性能和性价比的优质方案。
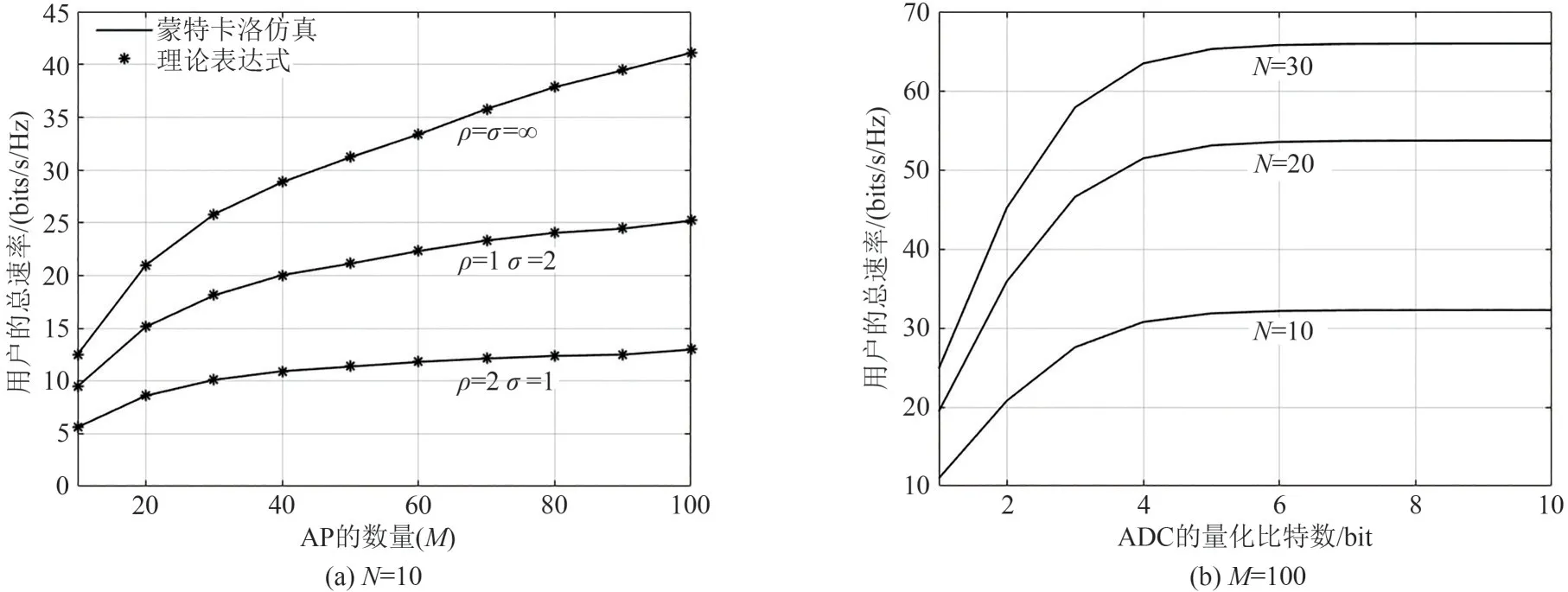
图2 用户的总速率与AP的数量或者ADC的量化比特数之间的关系Fig.2 The relationship between the total user rate and the number of APs or the number of quantized bits of ADC
当M=100、ρ=σ=4 bit和=1 bits/s/Hz 时,图3(a)对算法1的收敛性进行了仿真验证。通过观察可以发现,随着算法1的迭代次数不断增加,用户的整体速率性能不断增加,并且在迭代次数超过8 次之后,逐渐趋近于一个定值,这表明了算法1 会在8次迭代后逐渐收敛。另外,在M=100、N=10、ρ=σ=4 bit和=1 bits/s/Hz 的情况下,图3(b)比较了当系统使用算法1中的功率控制算法与不使用功率控制算法时,用户总速率的累计分布函数。通过观察,可以发现在系统不使用功率控制算法(图中虚线)的情况下,用户的总速率有95%的可能性大于31.8 bits/s/Hz;但是在系统使用算法1(图中实线)进行功率控制的情况下,用户的总速率有95%的可能性大于42.9 bits/s/Hz,这是无功率控制算法系统的1.35 倍。上述仿真结果验证了算法1 在提升系统整体速率性能方面的有效性。
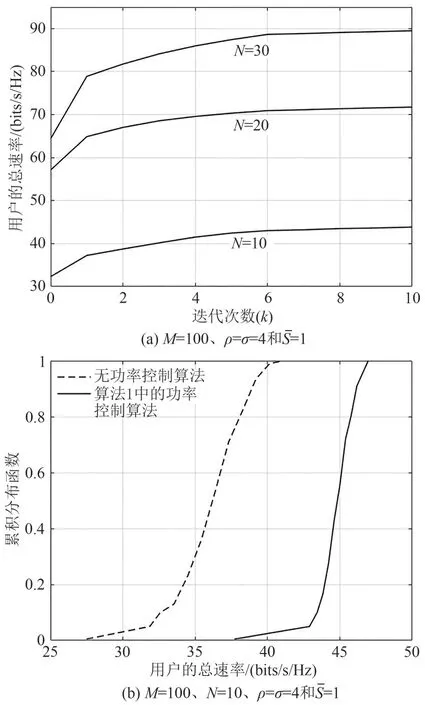
图3 使用功率控制算法时的用户总速率Fig.3 Total user rate when using power control algorithm
5 结论
本文首先介绍了莱斯信道下基于低精度ADC的去蜂窝大规模MIMO 系统模型、上行导频训练模型和下行数据传输模型。然后,推导了该系统使用CB预编码的可达速率闭合表达式,并根据速率闭合表达式,提出了一种能够提升系统整体速率性能的功率控制算法。最后,在不同的仿真环境下对系统的速率性能进行了比较和分析。仿真结果表明:(1)用户端ADC 量化器的精度对于系统速率性能的影响远超AP 端ADC 量化器的精度对于系统速率性能的影响;(2)当AP 和用户端使用的量化比特数超过4 bit 后,系统速率性能的提升将不再明显,因此AP 和用户端使用4 bit 的量化器是一种能够兼顾速率性能与性价比的优质方案;(3)针对95%可能性的用户总速率,相较不使用功率控制的情况,本文所提的功率控制算法可以提升35%的速率性能。

