基于码流的G-PCC压缩点云无参考感知质量评估

宋辉 苏洪磊 吕剑雨 元辉

（1.青岛大学电子信息学院，山东青岛 266071；2.山东大学控制科学与工程学院，山东济南 250061）

1 引言

随着现代媒体技术的快速发展，越来越多的技术被用于呈现三维（3-dimension，3D）内容，3D 数据也有了不同的格式，如全息图［1］、光场［2］、点云（point cloud，PC）［3］等。其中，点云是当前应用较为广泛的3D 媒体形式之一。点云是给定的坐标空间下的点的数据集合，每个点包含了坐标信息和属性信息（如颜色、法向量等），这些点共同来呈现为3D内容［4］。

由于原始点云数据量较大，因此在一定带宽限制的网络中传输点云时，需要对点云进行压缩［5］，导致点云失真，影响点云的感知质量。如何对点云感知质量进行实时有效的评估，及时改变点云压缩［6］和传输策略［7］，使用户获得更好的视觉体验，成为当前的研究难点。主观质量评估能准确反映点云感知质量，但其操作复杂，成本高，且无法镶嵌在实际的应用中对点云质量进行实时评估［8］。而客观质量评估能在点云系统中对点云进行实时评估，因此有必要研究点云的客观质量评价方法。

从输入信息的角度看，客观质量评估可分为参数规划模型、包层模型、比特流层模型［9］、媒体层模型［10-22］和混合型模型。点云的媒体层模型的输入信息是解码后的点云数据，需要完全解码获得体素［23］信息，因此耗费时间较长，无法适用于对实时性要求较高的点云传输系统。而比特流层模型不需要对点云完全解码，仅需从码流中提取必要的信息，即可做出对点云的感知质量评价。因此相对与媒体层模型来说，比特流层模型更适用于在实际应用场景中对点云质量进行实时监测。

目前，已有较多文献对点云质量评估（point cloud quality assessment，PCQA）进行了研究，但多为媒体层模型。文献［9］提出了一种简单的基于码流的PCQA 模型，对码率与点云感知质量的关系进行了研究。在媒体层模型中，全参考（full reference，FR）模型是目前的主流类型［10-20］。全参考模型可以分为基于点的模型［10-17］和基于投影的模型［18-19］。文献［9-11］中提出了Po2Point，Po2Plane 等利用几何信息进行点云感知质量评估的模型，这些模型主要通过计算失真点云与参考点云几何信息之间的差异对失真点云在几何层面做出感知质量评估，由于某些情况下点云的几何信息的差异并不会影响到点云的感知质量，故这些模型的性能不算理想。文献［13］提出了PC-MSDM 模型，该模型是3D网格质量评估算法的扩展利用了局部曲率信息，因此比单纯的利用几何距离差异的模型性能更好。除了基于点的模型外，文献［17］提出了基于图变换的GraphSIM 模型，该模型使用曲线图信号梯度作为质量指标来评估点云失真，对于具有多种失真类型的点云数据库具有良好的性能。另外，文献［18-19］提出了基于投影的PCQA 方法，将点云以某投影在平面上，再使用经典的图像质量评估算法进行计算，该类算法有较为优秀的性能表现。但是全参考PCQA 模型同时需要失真点云和参考点云，而参考点云在网络节点中是不易获取的，这就使得全参考PCQA 模型在实际的点云传输场景中无法使用。无参考（no reference，NR）模型不需要参考点云信息，文献［21］提出了一种基于深度学习网络的无参考PCQA 模型，该系统基于稀疏卷积层和残差的堆栈，提取层次特征并对其全局池化，从而得到网络的特征向量，由后续网络将特征向量输入到回归模块中预测最终客观质量分数。深度学习网络评估方法的高准确性需要经过大量的数据集训练来实现。对于小数据集的数据库，可能存在由于训练集不足导致性能降低的缺陷。并且该模型需要点云的媒体层特征，无法在点云系统中实时监测。

上述模型大部分为媒体层模型，需要对点云进行完全解码得到重建点云信息，故其计算复杂度较高，较难实现对网络中点云质量的实时监控。

本文提出了一种基于码流的G-PCC（geometrybased point cloud compression）压缩点云无参考感知质量评价模型。从压缩点云的码流中提取纹理量化参数（texture quantization parameter，TQP）、纹理比特率（texture bits per pixel，TBPP）和位置量化尺度（position quantization scale，PQS），本模型使用上述信息对点云进行感知质量评估。首先，在不考虑几何损失的情况下，确定TQP 与感知质量之间的关系。然后使用纹理量化参数和纹理比特率来预测纹理复杂度，并结合空域掩盖效应建立几何无损时的点云质量评估模型。然后结合位置量化尺度对点云下采样质量的影响，确定了纹理量化参数与位置量化尺度对点云质量的影响相互独立，并最终得到完整的点云质量评估模型。

2 基于码流的PCQA模型

G-PCC 是国际标准动态图像专家组（Moving Picture Experts Group，MPEG）提出多种3D 点云压缩（Point Cloud Compression，PCC）技术之一，主要应用于静态点云的压缩。点云在经过体素化后，进行几何和纹理编码，其中几何编码有八叉树（Octree）和Trisoup 两种方式，纹理编码有lifting 和区域自适应分层变换（Region Adaptive Hierarchical Transform，RAHT）两种方式。Octree 编码的程度可以在PQS 上体现，决定了点云的稀疏程度。纹理量化通过输入的参数对lifting 变换残差系数进行量化，TQP决定纹理上的量化误差。G-PCC点云压缩会进行纹理和几何的量化，而量化是G-PCC 压缩点云失真最主要的原因，分别对纹理编码和几何编码对点云感知质量的影响进行研究建立模型，并将他们结合形成一个整体的模型，图1 为基于码流的PCQA模型流程图。

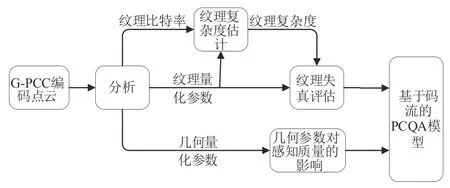
图1 模型流程图Fig.1 Flowchart of the model

2.1 纹理编码参数与点云感知质量之间的关系

几何无损的点云压缩会出现纹理失真，不同的纹理量化步长（texture quantization step，TQS）或其对应的TQP 会导致不同程度的纹理失真。为了研究TQP 与点云感知质量的关系，从WPC4 数据库1https://github.com/qdushl/Waterloo-Point-Cloud-Database-4.0中选取不同内容的点云（cake、cauliflower、glasses_case、litchi、pineapple、pumpkin、tool_box），在固定位置量化尺度的情况下（PQS=0.5），研究不同点云的主观质量分数（Mean Opinion Score，MOS）随TQS 的变化情况。WPC4数据集是在WPC［22］数据集基础上，选取其中的部分点云内容（bag、cake、cauliflower、glasses_case、honeydew_melon、litchi、mushroom、pen_container、pineapple、ping-pong_bat、pumpkin、ship、statue、tool_box），进行了G-PCC中的‘Octree+lifting’编码，PQS有三种不同的量化，分别为0.125、0.25、0.5，TQP 有四种不同的量化，分别为28、34、40、46，其余参数使用缺省配置。皮尔逊线性相关系数（Pearson linear correlation coefficient，PLCC）是衡量两数据集合线性相关程度的指标，其绝对值的取值范围为［0，1］，PLCC的绝对值越大，两数据集合线性相关程度越强。从表1 和图2 可以看出，对于特定的点云内容，其MOS值与TQS 有近似线性的关系，并且随着TQS 的变大，MOS 值变小。而对于不同点云内容来说，各曲线拟合直线的斜率有较大区别。比如，纹理复杂度高的点云（图3（a），cake），在相同的TQS 下具有更高的MOS值，也就是说它对应的斜率更大，相应的，纹理简单的点云（图3（b），tool_box），在相同的TQS下的MOS值较低，对应的斜率更小。

图3 原始点云：cake和tool_boxFig.3 Original PCs：cake and tool_box

表1 不同点云的MOS与TQS之间的PLCCTab.1 PLCC between MOS and TQS of different point clouds

图2 MOS与TQS之间的关系Fig.2 The relationship between MOS and TQS

造成这种现象的原因是人类视觉系统（human visual system，HVS）依赖于点云内容的纹理掩蔽效应在纹理失真评估中发挥了重要作用。因此，在建立点云的纹理失真模型中也需要考虑与点云内容相关的参数，即纹理复杂度（texture complexity，TC）［24］。

2.2 纹理复杂度估计

点云的纹理复杂度可以用原始点云局部块的像素值的平均标准差来表征。然而对于无参考PCQA 模型来说，原始点云不可获取。为了克服这个问题，使用来自压缩点云的码流信息（如TQP 和TBPP）来估计TC。选用14 个不同内容的点云（bag、cake、cauliflower、glasses_case、honeydew_melon、litchi、mushroom、pen_container、pineapple、ping-pong_bat、pumpkin、ship、statue、tool_box），在固定TQP 的情况下TBPP 与TC 的关系如图4 所示，当TQP 固定时，TBPP 和TC 之间的关系是近似线性的，并且这个线性函数的斜率和截距是TQP的函数：

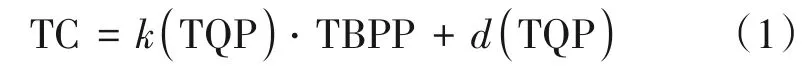
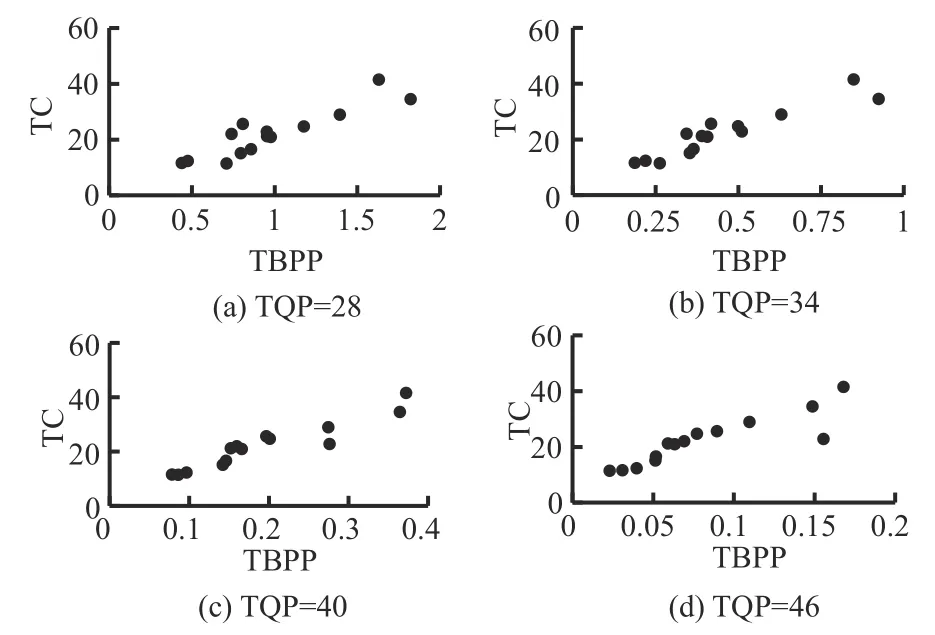
图4 不同TQP下TBPP与TC的关系Fig.4 The relationship between TBPP and TC under different TQP

k和d是TQP的函数。为了研究k和d与TQP的具体关系，将图4 中拟合直线的斜率和截距随TQP 的变化在图5 中表示。可以看出，k（TQP）与d（TQP）可以用线性函数表示。

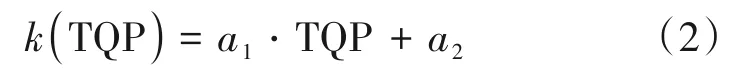
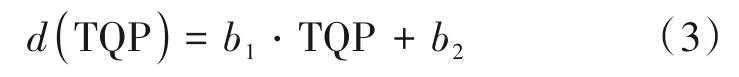
其中a1、a2、b1、b2是在最小二乘误差准则下通过使用图5中的数据进行训练而获得的常数。

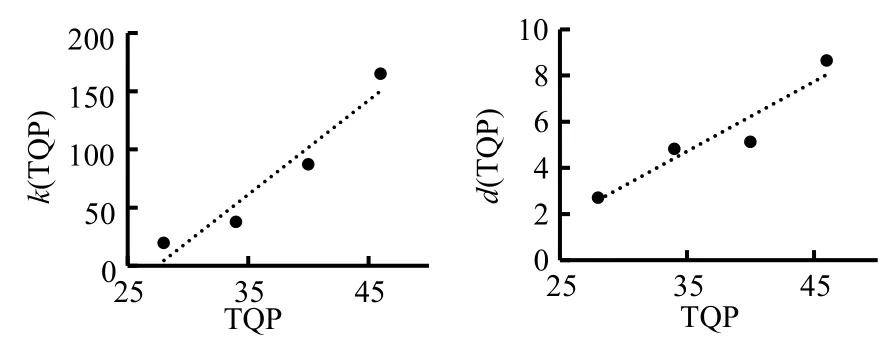
图5 不同TQP下的斜率和截距Fig.5 Slope and intercept of fitting line in Figure 3 below for different TQP

2.3 纹理失真评估模型

正如图2 中那样，不同内容点云的MOS 值与TQS具有线性关系：

其中α和β是实验参数，MOST代表纹理失真点云的MOS值，并且

可以看出β是MOST的最大值，不同点云之间的β差别不大，可以设为一个常数。同时可以观察到，点云内容不同，α也不同。图6 示出了α和TC 的散点图，其中较高的α值通常对应于较高TC 的点云（例如cake），反之亦然（例如tool_box）。因此，可以采用以下函数对α进行估计：

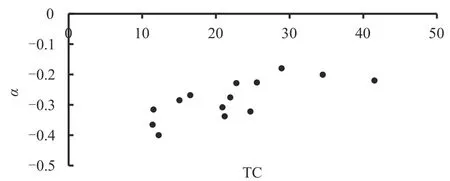
图6 α和TC的散点图Fig.6 Scatter plots of α and TC

其中c和d是通过使用最小二乘法拟合训练获得。结合式（4）～（6），可以得到：

该模型可用于评估G-PCC 纹理失真点云的感知质量，也可作为同时具有纹理和几何失真的PCQA 的关键的一部分。

2.4 包含几何失真的PCQA模型

G-PCC 编码不仅在纹理上对点云进行了编码，也在几何上对点云进行了下采样，从图7 中可以看出，对于所有点云来说，在相同的PQS 条件下，MOS随着TQP 的增大而减小，而在同样的TQP 条件下，PQS 越小，MOS 值越小。图中圆形表示PQS=0.5 的数据值，方形表示PQS=0.25 的数据值，三角形表示PQS=0.125的数据值。

图7 不同PQS下TQP与MOS的关系Fig.7 MOS vs.TQP at different PQS

为了研究TQP 和PQS 的对点云感知质量的影响是否独立，用每个点云在不同PQS 下TQP 与归一化MOS 值（NMOS）的关系进行研究如图8 所示，NMOS定义如下：

图8 不同PQS下TQP与归一化MOS的关系Fig.8 Normalized MOS vs.TQP at different PQS

其中TQPmin为TQP 的最小值（28），图中圆形表示PQS=0.5 的数据值，方形表示PQS=0.25 的数据值，三角形表示PQS=0.125的数据值。

可以看出，与图7 相比，图8 中的曲线有很大程度的重合，这表明TQP 和PQS 之间具有显著的独立性，这也意味着点云的纹理和几何失真对点云质量的影响是独立的［25］。因此可以在前面纹理失真模型（PQS=0.5）的基础上，研究点云感知质量随PQS的减小而减小的程度。

因为是在PQS=0.5的纹理失真模型的基础上研究PQS是如何影响点云感知质量的，所以先求出同一PQS下所有点云的MOS的均值，并除以PQS=0.5时的MOS均值进行归一化，称为归一化的MOS均值，它可以表示PQS 对MOS 的影响程度，研究其与PQS 的关系，如图9所示，采用以下模型来预测随PQS的变化归一化的MOS均值的下降比例：

图9 PQS与归一化MOS均值的关系Fig.9 Relationship between PQS and Normalized MOS Mean

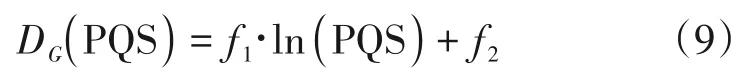
f1和f2是经过数据拟合后得到的参数，DG（PQS）是归一化的MOS均值随PQS的减小衰减的程度。

由于可以认为纹理失真与几何失真对点云的MOS 的影响几乎是不相关的，因此，本文提出了基于码流的G-PCC 编码点云的无参考感知质量评价模型：

3 实验结果与讨论

本文实验所用的数据集为WPC4点云数据库，选用了其中14个不同内容总计168个失真点云。

通过训练得出模型中各个参数的值在表2中给出，具体来说，β是点云MOS值的最大值；参数a1、a2、b1、b2通过公式（2）、（3）得出；参数c、d通过公式（6）得出；参数f1和f2通过公式（9）得出。这些参数在本模型中固定。

表2 参数值Tab.2 Parameter values

为了验证本模型的性能，采用传统的三个指标，也就是PLCC、斯皮尔曼秩相关系数（Spearman rankorder correlation coefficient，SRCC）、均方根误差（root mean square error，RMSE）进行评估。PLCC 和SRCC越接近1，预测MOS 值与实际的MOS 值的相关性越好，RMSE 越小，预测MOS 值与实际的MOS 值之间的误差越小。

进行了消融测试以验证纹理失真模型和几何失真模型分别对总体模型的贡献，使用上述所说的三个指标（PLCC、SRCC、RMSE）分别对纹理失真模型和几何失真模型进行检测，测试结果如表3所示，可以看出，纹理失真模型和几何失真下降率都对质量评估产生了积极的影响。

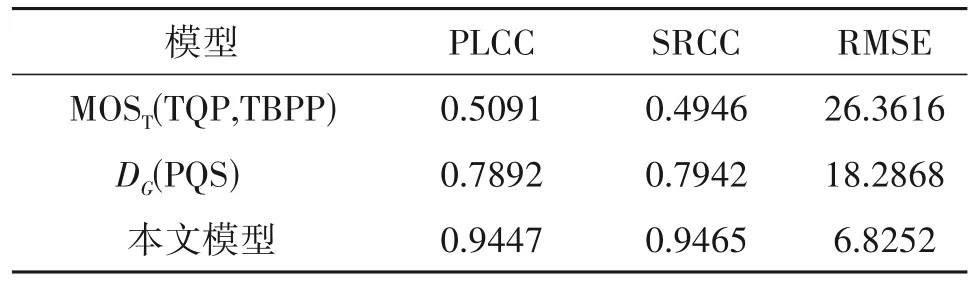
表3 消融测试Tab.3 Ablation test results

为了评估该模型的泛化能力且为了防止数据的过度拟合，本文模型在WPC4 数据库进行留一法测试，测试的结果在表4中呈现。

在测试数据中的三个统计指标方面评估了所提出模型的性能，从表4中可以看出，该模型对于每一个点云的性能都是优异的，并且平均值和标准差值都能够表示该模型具有强大的泛化能力和较好的鲁棒性。

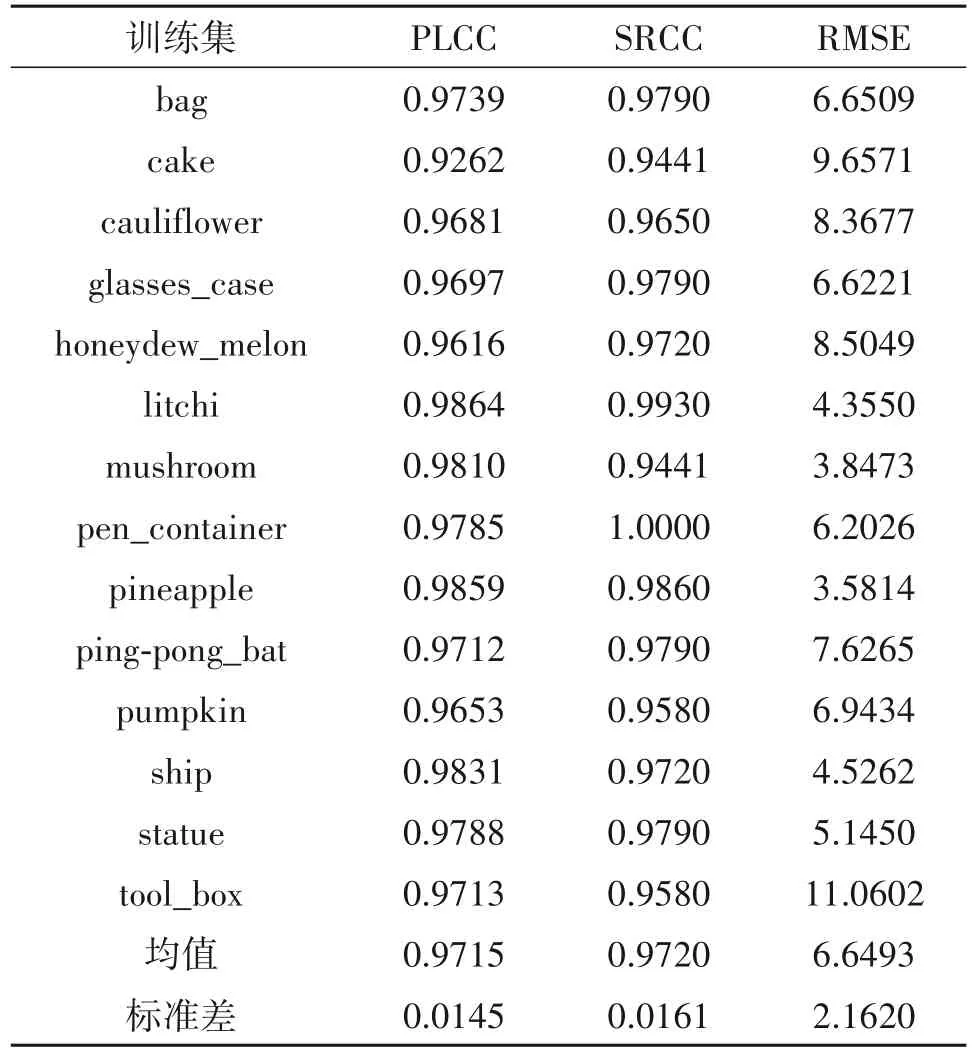
表4 留一法测试Tab.4 Performance of the LOOCV results

另外，为了进一步验证本文模型的性能，将本文模型与其余先进的PCQA 模型进行了性能参数比较，结果表5所示。

表5 中最佳结果以粗体显示，次佳结果用斜体显示。从表中可以看出，以WPC4 点云数据中G-PCC 编码数据集为评估对象时，本文模型与其他PCQA 模型相比具有明显的优势，本文模型的PLCC和SRCC 均达到了0.94 以上，说明该模型所得客观分数与主观质量分数之间有优异的相关性。其次是GraphSIM 指标，其PLCC 与SRCC 分别为0.9224和0.9227，与本文模型相比略差，其余PCQA 指标，相关性均在0.8 以下。图10 展示了各算法所得客观质量分数与主观质量分数的散点图。

图10 各算法所得客观质量分数与主观质量分数的散点图Fig.10 Scatter chart of objective quality score and subjective quality score obtained by each algorithm

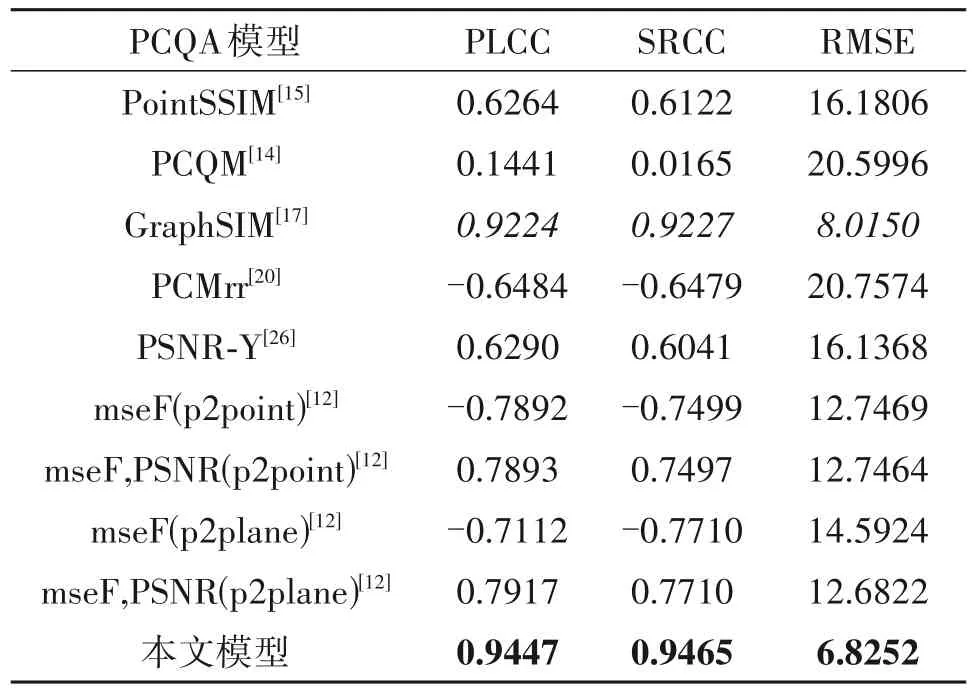
表5 与其他PCQA模型的对比Tab.5 Comparison with other PCQA modes

为了验证本文模型只需要较低的计算成本，选取了两个具有代表性的点云，他们具有不同的内容复杂度，将本文模型在表6 中与其他PCQA 模型的时间复杂度进行比较。其中不包括mseF（p2point），mseF，PSNR（p2point），mseF（p2plane），mseF，PSNR（p2plane），它们的执行时间与PSNR-Y 相当。本测试在该测试在配备3.6 GHz Intel（R）Xeon（R）W-2123 处理器和32 GB RAM 的戴尔Precision 5820 Tower上进行。

表6 PCQA模型的时间复杂度Tab.6 Time complexity of PCQA models

本文模型的执行时间明显低于其他模型，其他模型随着点云中点的个数的增加执行时间会明显增加，而本文模型则没有，可以说明本文模型具有较低的时间复杂度，节省计算成本。

4 结论

本文提出了一种基于码流的G-PCC 压缩点云无参考感知质量评估模型。通过分析纹理编码参数与点云感知质量的关系，发现不同内容点云的在相同编码条件下的感知质量是不同的，并且纹理参数与感知质量呈线性关系。通过研究码流中TBPP 信息与TC 的关系，建立TBPP 对TC 的预测模型并建立G-PCC 编码点云的纹理失真模型。通过分析位置量化尺度与MOS 的关系建立几何下降率模型并结合纹理失真模型建立基于码流的G-PCC压缩点云无参考感知质量评估模型。实验结果表明，本文模型所得的客观分数与MOS 有较好的一致性。