基于公理设计和多色集合的树障清除机器人方案设计
杜 轩,李宝万,方子帆
(1.三峡大学 水电机械设备设计与维护湖北省重点实验室,湖北 宜昌 443000;2.三峡大学 机械与动力学院,湖北 宜昌 443000;3.机器人与智能系统宜昌市重点实验室,湖北 宜昌 443000)
0 引言
架空输配电线路是电力系统中实现电力输送的基础设施,是提高供电稳定性与安全性的关键。但在线路实际运行过程中,由于线路通常架设于室外,其电力输送效果极易受到自然环境影响[1]。电力线路沿线树障是影响电力线路运行的安全隐患之一,在电力线路的运行维护中,常采用人工的方式对影响线路安全的树障进行清除,维护人员借助专用工具攀爬到树上,采用锯、砍等方式对树障实施清除,这种人工的方式存在较大的安全隐患,在工作中触电引发人员伤亡的事件屡有发生,且人工清除方式受环境影响,工作效率低下。考虑到人工清理架空电力线路沿线树障的危险性,机器人有望在未来帮助或取代人来执行这些任务。
由于使用环境的复杂性,关于树障清除机器人设计的研究相对匮乏,尚无实用的树障清除机器人。目前国内外学者对爬树机器人、爬树修枝机器人展开了大量的研究,对该类机器人的研究主要集中在对机器人攀爬机构的设计。其中比较典型的有机器人WOODY,主要被设计用来代替工人清除树枝。该机器人通过用手臂环抱整个树干,伸展和收缩身体完成爬树动作[2]。ISHIGURE等[3]也开发了一种用于修剪树木的攀爬机器人,其结构类型属于连续运动式攀爬机器人,它使用了一种受伐木工人启发的抓取机制,以及基于轮子的垂直攀爬驱动系统。ALMONACID等[4]提出一种利用Gough Stewart平台进行机动的攀登机器人,它可以爬上一个没有树枝,但有一定弯曲范围的树干,比上述两个机器人具有更大的可操作性,但是实际应用还需作出改进。香港中文大学徐扬生院士团队[5-6],研制了一种新型灵活爬树机器人“Treebot”,该机器人依照仿生学原理,模仿尺蠖的爬行方式,在树干不规则的树木上攀爬具备较高的机动性,但该攀爬结构的尺寸较大,在树枝较多的地方攀爬受到一定限制。上述研究成果对树障清除,机器人的攀爬机构设计以及关键技术的突破具有一定的参考价值。但电力线路树障清除机器人所需的功能更加丰富,针对架空电力线路的树障清理任务要求,机器人除了攀爬还需要有一定的避障能力,即在完成爬树基本功能的同时,还应具有避开无需清理的树枝障碍,清理指定树枝的功能,因此树障清除机器人的设计具有更多的设计约束和要求,需要解决机器人的机械结构创新设计问题,对树障清除机器人的方案设计提出了更高的要求。在机械产品的方案设计领域,相关学者也提出了一些有效的方法。高新勤等[7]对多色集合(Polychromatic Set,PS)理论在概念设计建模和推理技术中的应用进行了相关研究;MARSDTTIR等[8]研究了公理设计(Axiomatic Design,AD)在一款名为Chessmate的下棋机器人方案设计中的应用;LI等[9]提出一种螺杆传动管内机器人公理化设计方法;ZHU等[10]提出了基于公理设计的定制化下肢外骨骼康复机器人概念设计方法;杨得玉等[11]提出了基于公理设计和多色集合的拆卸设备方案设计;肖人彬等[12]提出了基于模糊信息公理的设计方案评价方法并应用于产品的方案设计。以上成果对本文的机器人方案设计研究具有一定的参考价值。
通过对已有研究内容工作的分析,为了实现在树干上自动爬行,并清除影响电力线路安全运行的树障,需要在方案设计阶段进行创新设计。将公理设计对设计过程结构化表达和多色集合逻辑推理的优势相结合,在设计过程中,通过公理设计的功能结构映射过程,及时地检查设计过程的合理性,并对设计方案进行正确评价,同时利用多色集合建立约束表达模型,对设计方案进行推理,最终得到满意的设计方案。首先,针对电力线路树障清除机器人设计要求,建立基于公理设计的功能—结构模型,并利用独立性公理保证分解的独立性。然后,基于结构库构建树障清除机器人的多色集合层次结构模型,以实现其功能—结构快速映射和树障清除机器人方案的计算机辅助快速设计,通过约束条件的形式化描述得到约束矩阵,排除存在约束的方案,得出可行方案,使用模糊信息公理的评价方法得到满意的设计方案。最后,根据设计方案制作样机进行实验,针对实验结果进行分析验证设计方法的有效性和设计方案的可行性。为了表述方便,除特殊说明外,下文中的机器人特指架空电力线路树障清除机器人。
1 机器人设计需求
树障清除机器人用于架空电力线路廊道沿线的树障清理,树障清除机器人的作用对象为高大的乔木,不同树木直径不同,与架空电力线路构成的隐患情况不同。机器人通过电力线路维护人员携带至需要清理的树木下进行攀爬清理作业,作业过程中需要对隐患进行识别,并绕开无需清理的树枝,到达指定位置进行清障作业。根据其工作的特殊环境以及作用对象,树障清除机器人具有以下设计要求:
(1)体积小,质量轻,结构紧凑便于携带;
(2)在一定负载下,能以期望的速度在树上实现稳定爬升;
(3)具有一定的适应能力,可以适应不同直径的树木;
(4)可以对树障隐患进行识别;
(5)修枝清障机构要可控,电锯切割位置可以调节,防止树枝咬合,砸到机器人,避免砍伐树障时树倒向输电线路一侧或将人砸伤等意外情况;
(6)要具有一定的障碍识别和越障能力,绕过不需要清理的树枝;
(7)在故障时,具有一定的自保防坠措施;
(8)对动力能源信息具有检测功能,供应不足时报警。
2 机器人功能结构设计
2.1 公理设计概述
20世纪90年代SUH教授[13]通过多年的研究和实践,总结归纳了设计的基本公理和原则,并于1990年出版了专著《设计原理》,公理设计理论由此产生。公理设计主要用于解决设计方案是否可以满足产品的功能需求,满足的程度如何以及多个设计方案的选择等问题。公理设计理论将设计过程分为用户域、功能域、结构域和工艺域。功能域代表设计方案的功能需求,功能需求要满足可能的约束条件。结构域描述设计方案的设计参数,工艺域表达用于实现设计参数的过程变量。
公理设计的设计过程就是4个域间的逐层分解、迭代和映射的过程。在公理设计中,从功能域到结构域,再从结构域到工艺域,按照层级的“之”字映射进行展开。在两个域进行映射的过程中,要求同一个层次的映射完成后,才能进行下一层次的分解,反复迭代直到低层次或不能展开为止,分解过程中使用独立性公理保持功能要求的独立性,使得方案的设计更加合理,可有效减少无效方案的产生。信息公理力求设计信息的含量最少,通过对设计方案信息含量的计算和比较可选择出较优的设计方案。
产品的功能需求可以通过用户的需求映射得到,从功能域到结构域之间的映射过程是公理设计关注的重点,通过对产品的功能需求逐级分解得到产品功能需求的层次结构树,再通过逐级映射得到产品的拓扑结构和结构库。功能域和设计域之间的映射过程可以通过式(1)表示:
(1)
式中:FRn表示功能域中的特征向量,用于描述功能需求;DPn表示结构域中的特征向量,用于描述设计参数;[A]为设计矩阵,其中元素Anm表明功能域和特征域中特征向量的相关性,Anm=0表示FRn和DPm没有关联,Anm=常数X表示FRn和DPn相互关联。
在设计过程中可通过设计矩阵的类型判断该设计是否符合独立性公理,公理设计中根据设计矩阵[A]的对角矩阵、三角矩阵、非对(三)角矩阵3种形式将设计类型分为独立设计、解耦设计和耦合设计。独立设计满足独立性公理,是较好的设计类型,解耦设计也可满足独立性公理,但是需要保证设计参数遵循一定的规律。
2.2 机器人公理设计功能—结构模型
机器人的用户需求{CA}为使用机器人代替人工攀爬树木,清理架空电力线路廊道周围构成树障隐患的树木枝干。根据公理设计的“之”字型映射得到总的功能需求{FR}是能够攀爬树木并清理树障的机器人,总的约束{C}为树木的情况,例如不同树木的直径不同、同一树木不同高度直径的变化、树枝的分布、构成树障隐患的枝干位置等。将采用“之”字型映射方法将总的功能需求{FR}进行分解得到功能需求FRs,再将功能需求{FR}转化成设计参数{DP}得到设计参数DPs。下面将功能需求{FR}和设计参数{DP}进行第一级分解。
(1)功能需求{FR}第一级分解
FR1:携带一定负载攀爬树木并避开障碍树枝到达指定位置;FR2:切除构成对输电线路树障隐患的树枝、树冠部分;FR3:在攀爬过程中,出现断电故障时不会坠落,不被切除的树枝树干砸坏,可以保障机器人自身安全;FR4:机器人可以远程控制,可以获取机器人周围的环境信息并回传到控制端,动力能源信息可以报警反馈;FR5:可以储备能源用于机器人的动力供应。
(2)设计参数{DP}第一级分解
DP1:攀爬运动结构;DP2:切割执行结构;DP3:安全防护结构;DP4:控制监测系统;DP5:动力供应系统。
第1层设计公式为:
(2)
再将第一级分解得到的功能需求{FR}和设计参数{DP}逐级分解得到第2层机器人的功能需求和设计参数的分解结构及设计公式表如表1所示。通过设计公式可以看出设计类型均为解耦设计或独立设计,满足独立性公理。

表1 FR、DP分解及设计公式表
2.3 功能—结构分解结果
通过逐级分解得到机器人的功能需求分解图如图1所示。

通过第1层分解得到的设计矩阵[A]为下三角矩阵,这样的设计为解耦设计,满足独立性公理,其中FR3与DP1、DP3相互关联,因此其设计结构需要遵循一定的规律。第2层分解得到的功能需求和设计结构影响矩阵如表2所示。可以看出,影响矩阵整体为下三角矩阵,满足独立性公理,其中的FR11、FR12、FR13、FR31、FR42、FR43等功能与其对应结构之间存在着关联,因此其设计结构也应遵循一定的规律。

表2 机器人的功能需求和设计结构影响矩阵

续表2
3 基于多色集合的机器人方案推理
多色集合理论是一种新的信息描述和处理的数学工具。经典多色集合由6个基本成分组成,其表达式为PS=(A,F(a),F(A),[A×F(a)],[A×F(A)],[A×A(F)])。集合及其着色的自相关矩阵[A×A],[F(a)×F(a)],[F(A)×F(A)]以及着色之间形成的矩阵[F(a)×F(A)]也是常用的一些布尔矩阵,可以根据建模需求添加这些成分。在多色集合中,元素和集合都可以被着色,可以很好地用来描述功能分解和设计参数分解之间的关系,因而可以用多色集合理论建立功能分解和可行方案求解的推理机制,得到机器人结构设计的可行方案。
3.1 功能结构的多色集合层次结构模型
将机器人按照功能—方法逐级分解后,在各功能之间、功能的实现方法之间以及外部环境和功能与方法之间可能存在约束关系,因此使用包含约束信息的功能方法树模型,利用多色集合理论对传统的层次结构增加节点颜色和约束关系,并区别节点之间连接关系的具体类型,给直接分解关系和间接约束关系涂上不同的颜色,建立机器人设计的形式化结构模型。在机器人的多色集合的层次结构模型中存在以下3种约束关系:某一功能与实现这一功能的方法之间的直接约束关系,记为F1(c);同一层次各个功能之间存在的间接约束关系,记为F2(c);实现不同功能的方法之间存在的约束关系,记为F3(c)。建立约束关系的集合为F(c)={F1(c),F2(c),F3(c)}。建立机器人的PS层次结构模型如图2所示。

在G*={A*,C*}中一共有30个节点,内部节点其集合形式表示为:
A*={F(A(k,ik,jk-1));A(k,ik,jk-1)}。
(3)
其中A(k,ik,jk-1)为第k层,第ik个节点。其父节点为k-1层的第jk-1个节点;F(A(k,ik,jk-1))为第k层、第ik个节点的颜色,它描述了节点的性能、参数等属性。
方案元层A(2,1,1)=a1a2a3,A(2,2,1)=a4a5a6a7a8,A(2,3,1)=a9a10,A(2,4,2)=a11a12,A(2,5,2)=a13a14,A(2,6,3)=a15a16,A(2,7,3)=a17a18,A(2,8,4)=a19a20a21a22a23a24,A(2,9,4)=a25a26a27,A(2,10,4)=a28a29a30a31a32a33a34,A(2,11,5)=a35a36a37a38,A(2,12,5)=a39a40。

表3 各层功能元所表示的物理意义

续表3
3.2 约束条件的形式化描述与方案推理
机器人的PS层次结构模型中的约束构成的边集E由内部各个节点之间的连线构成,其中内部节点的边可以通过节点集合的自相关矩阵得到。内部约束矩阵
(4)
其中:i=j=30;ci_j为0或1,ci_j=0表示节点间不存在约束关系,ci_j=1表示节点间存在约束关系。根据各个节点的约束关系可以得到共34条边。将满足条件=1的元素构成的集合记为边集E:
E(e)={e1,…,en}={c2_1,c3_1,c4_1,c5_1,c6_1,
c7_2,c8_2,c8_7,c9_2,c9_8,c10_3,c11_3,c12_4,c12_11,
c13_4,c13_7,c14_5,c15_5,c15_14,c16_5,c17_6,c18_6,c19_7,
c20_8,c21_9,c22_10,c23_11,c24_12,c25_13,c26_14,c27_15,
c28_16,c29_17,c30_18},
其中n=34。将约束关系类型的集合F(c)={F1(c),F2(c),F3(c)}看作是3类不同边的着色,边E与边代表的约束类型F(c)之间的关系采用多色集合[A×F(a)]进行描述得:
F1(c)F2(c)F3(c)
(5)
其中F1(c)=1的边有Ef1(e)={c2_1,c3_1,c4_1,c5_1,c6_1,c7_2,c8_2,c9_2,c5_2,c10_3,c11_3,c12_4,c13_4,c14_5,c15_5,c16_5,c17_6,c18_6,c19_7,c20_8,c21_9,c22_10,c23_11,c24_12,c25_13,c26_14,c27_15,c28_16,c29_17,c30_18},按照布尔矩阵[F(A)×F(A)]或[F(a)×F(A)]建立如下推理矩阵:
M2_1=[F(A(1,1,0),A(1,1,0))×F(A(0,0,0),A(0,0,0))],M3_1=[F(A(1,2,0),A(1,2,0))×F(A(0,0,0),A(0,0,0))],…,M30_18=[A(2,12,5)×F(A(2,12,5))]。
其中F2(c)=1的边有Ef2(e)={c8_7,c9_8,c15_14}按照自相关矩阵[F(A)×F(A)]建立如下推理矩阵:
M8_7=[F(A(2,2,1))×F(A(2,1,1))],…,M15_14=[F(A(2,9,4))×F(A(2,8,4))]。
其中F3(c)=1的边有Ef3(e)={c12_11,c13_7},按照自相关矩阵[F(A)×F(A)]建立如下推理矩阵:
M12_11=[F(A(2,5,2))×F(A(2,6,3))],M13_7=[F(A(2,1,1))×F(A(2,7,3))]
为了表述方便,将矩阵M2_1~M30_18画在图3a上,其中①~分别为M2_1~M30_18;将矩阵M8_7,M9_8,M12_11,M13_7,M15_14画在图3b上,记为~;带有底色的为约束矩阵。
按照布尔矩阵[F(A)×F(A)]或[F(a)×F(A)]建立的推理矩阵描述的是某节点属性与其他节点属性之间的关系,将两节点所包含功能元或方案元进行比较,不存在约束关系的两功能元或方案元用“”标记。实际推理过程中,可以先依据总的约束信息{C}排除不满足条件的功能元包含以上功能元的方案不满足约束条件,不再继续向下推理,根据推理矩阵M2_1~M30_18推理方案,对比约束矩阵M8_7~M15_14排除同时包含存在功能元冲突的方案,可提高推理效率,最终得到共54个可行方案。


P=Chioce{F(A(0,0,0))}+Chioce{F(A(1,1,0))}+
Chioce{F(A(1,5,0))}+Chioce{F(A(2,1,1))}+
Chioce{F(A(2,2,1))}+Chioce{A(2,2,1)}+
(6)
式中chioce表示在节点包含的功能元或可行方案元中随机选择一种,所有可行方案包含其中,但式中仍有存在约束的方案。
4 基于模糊信息公理的方案评价与择优
因为设计方案涉及的因素较为复杂,具有随机性、模糊性的特点,无法给出所评价功能元、方案元因素指标的具体数值,无法使用传统信息公理对每个方案的信息量进行准确计算,所以采用改进的模糊信息公理方法。将各方案关键节点作为一个子设计系统,确定其设计范围及系统范围,求解出模糊信息含量,继而求解整个方案的总模糊信息含量。根据专家的知识与经验、相关学者研究及作者分析,确定了功能性指标、经济性指标、社会性指标3个方面的9个子功能指标,以及对应指标权重[14](如表4)。

表4 机器人设计方案关键节点的各项评价指标
根据指标的类型,将以上9个子功能指标分为效益型指标、成本型指标、区间型指标,其中效益型指标包括攀爬速度、承载能力、续航时间、可靠性;成本型目标包括可制造性、制造成本;区间型指标包括结构复杂度、环境适应性、可操作性。依据不同类型指标的属性,将各个指标及其对应评价等级进行划分,如表5所示。

表5 各项指标及对应评价等级表

续表5
根据各个功能指标的评价等级对机器人设计方案中关键节点的功能元及方案元进行评价,确定各个指标的模糊系统范围以及模糊公共范围,从而计算出各个功能元及方案元的模型信息含量。设计范围明确功能需求,系统范围体现设计方案的实际性能,模糊设计范围与模糊系统范围的交集称为模糊公共范围。以可操作性为例,各功能元及方案元对应的定性评价指标如表6所示。

表6 各功能元及方案元可操作性定性评价指标
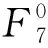
(7)

计算出各功能元及方案元可操作性信息含量如表7所示。

表7 各功能元及方案元可操作性信息含量计算结果
通过计算9个指标的模糊信息含量,得出模糊信息总量最小值为34.812 34,根据公理设计的信息公理,其对应的方案P11和方案P14是较好的设计方案,该评价结果与实际情况较为符合,

5 实验验证
5.1 需求实现情况验证
为了验证了设计方法的有效性,选取了信息含量最小设计方案P11、P14及信息含量较小的设计方案P8,制作出模型机如图5所示。设计方案P11使用一组夹紧机构,机构位置位于机器人上部,末端使用90°全向轮。设计方案P14使用一组夹紧机构,机构位置位于机器人中部,末端使用90°全向轮。设计方案P8整体结构上下两组夹紧机构,夹紧机构末端使用麦克纳姆轮或90°全向轮。将设计方案P8末端两种情况分为P8a、P8b两种子方案,子方案P8a如图5c所示,其夹紧机构末端和攀爬运动机构均采用麦克纳姆轮,子方案P8b如图5d所示,其夹紧机构末端采用90°全向轮和攀爬运动机构采用麦克纳姆轮。以上4种设计方案制作出的模型机在实验中均能基本满足攀爬、清除树障等功能需求。

5.2 结构合理性分析
实验中设计方案P11(如图5a)采用一组夹紧机构位于机器人上部机器人重心整体偏下,具备较好的夹紧以及偏心自锁的效果。在树干直径发生变化时,可以较容易地调整夹紧机构的夹紧程度,机器人向上攀爬时,位于夹紧机构末端的全向轮接触受力情况良好。设计方案P14(如图5b)采用一组夹紧机构位于位于机器人中部,可以实现基本的功能需求,但机器人向上攀爬中容易出现后倾导致驱动电机发热严重,并且不易调整姿态至正常位置。
实验中,设计方案P8的两个子方案P8a、P8b使用两组夹紧机构,夹紧效果更好,但是对于轮组运动产生的阻碍和更为突出,由于树干直径的变化,树干截面形状的不规则、树干表面凸起等情况使得轮组控制复杂,夹紧机构需要不断调整。当轮组中一个轮受到阻碍时将对整个轮组的运动产生阻碍。这两种方案并不能很好地实现机器人沿着树干周向移动的功能。
通过对不同结构的验证实验结果分析,相比较方案信息含量最小的方案P11、P14,使用上下两组夹紧机构的方案P8其结构更加复杂,整体承载增加,使其攀爬速度降低,使用时间缩短。在实际制作中使用原材料及加工成本也较高,控制也相对复杂,对于环境的适应性和可操作性较差,可靠性降低。可以看出,通过对设计方案功能元或方案元进行评价后再使用计算模糊信息含量总量的方式评价方案具备实用性和有效性。
5.3 整机方案验证
通过对整机各个机构功能实现情况进行测试,对直径范围在25 cm~30 cm的树干都有较好的夹持环抱,贴合紧密。机器人可以实现预期的携带电锯总负载23 kg完成抱紧、上下攀爬位姿调整功能,树障清除装置可以实现切割位置的调整以及对树干和树枝的切割功能。实验结果验证了采用半环抱夹紧结构,留出开口这种思路可行,能保证夹紧同时稳定上下攀爬,树况良好情况下可实现绕树周小幅旋转,同时在机器人出现歪斜,后倾等情况后,可以进行位姿调整,可手动调整至竖直攀爬状态,但当树表面粗糙以及有树瘤等情况时,可通过摄像头观察树况移动至树况较好位置进行环绕树周旋转实现避障功能。对一组夹紧机构设计方案基础上进行改进,在夹紧机构末端使用上下两组90°全向轮(omni wheel)。在实验中,当需要调整机器人位置如图6a时,可以通过控制机器人沿着树干周向移动的功能调整至如图6b。机器人能够实现预期的所有功能需求,满足相应的设计需求,通过实验验证了整个设计方法的有效性和设计方案的可行性。

6 结束语
在机器人设计中使用公理设计的“之”字型映射方法可以完成功能需求的分解,得到完整的各层功能分解结构,并通过独立性公理保证各个功能需求分解的独立性。包含约束信息的多色集合层次模型可以很好地描述各个层次功能结构之间的约束关系,以及外部环境与功能需求之间的约束关系,通过约束信息的形式化表达,构建推理矩阵进行设计方案的推理,完成从功能需求到设计方案的逐层求解。
由于机器人功能结构的复杂性,其设计方案由较多的功能元或方案元构成,由于各个功能元或方案元具有模糊性和随机性,不便得出定量的数值,无法使用传统的信息公理计算每个方案的信息含量,若使用定性评价指标评价方案则评价不够全面且存在一定的主观性,在实际使用中通过对方案元或功能元定性评价再计算设计方案的模糊信息总量的评价方法可以避免单独使用某一方法的不足,并得出较为全面准确的评价结果。
通过对推理得出方案进行实验分析,验证了设计方法的有效性和设计方案的可行性,同时,公理设计与多色集合的结合也有利于设计方案的创新,采用本方法设计的树障清除机器人在结构上具备较好的创新性,依据以上设计方案申请的国家发明专利也获得了授权(ZL201910803014.X)。本文所研究的树障清除机器人的设计侧重于应用机械设计理论方法完成机械结构的创新设计,对于机器人的运动学及动力学分析,以及机器人的智能控制还有待进一步的分析和研究,后期将进一步研究树障清除机器人的自动控制以及树障隐患的模式识别问题,借助视觉导航及路径规划等技术实现机器人的自主作业。

