基于球头刀具的螺旋锥齿轮齿廓倒棱轨迹规划＊

胡 敏 洪荣晶 孙小敏 张建坤 林晓川

（①南京工业大学机械与动力工程学院，江苏南京 211816；②南京工大数控科技有限公司，江苏南京 211899）

与其他普通的齿轮相比，螺旋锥齿轮承载能力强、传动效率高且噪声小，这些优点使得螺旋锥齿轮被广泛用于各个领域。但是，在加工过程中，加工刀具对螺旋锥齿轮毛坯的切齿，会在其两端的齿廓处留下残刺，这些残刺大大增加了齿轮啮合时的磨损，造成传动不稳定，并降低齿轮的使用寿命，因此在完成齿轮的加工后需要进行齿廓倒棱[1]。由于螺旋锥齿轮齿廓倒棱多为自由曲面，现有的倒棱方式多以手工倒棱为主，国内外未见公开的螺旋锥齿轮齿廓倒棱的技术文献报道。然而，手工倒棱会带来很多明显的问题：加工效率低下、工件的表面难以保证以及工人的工作环境恶劣等。随着五轴加工机床的诞生，在解决自由曲面加工问题上起到了很大的作用。但是，额外的两个旋转轴在轨迹规划上也产生了很多问题。为了实现螺旋锥齿轮在五轴机床上进行倒棱加工，有必要针对倒棱轨迹规划上深入研究。

在倒棱研究方面，公开的技术文献对螺旋锥齿轮齿廓倒棱研究少之又少。翟明伟[2]设计的端面齿廓旋分倒棱刀具实现渐开线圆柱齿轮齿廓倒棱的连续分度加工，极大地提高了加工效率；张亚斌[3]针对齿轮齿廓倒角加工过程的研究，以渐开线圆柱齿轮为对象，开发出直齿圆柱齿轮数控齿轮倒角加工软件；李佳等[4]为解决螺旋锥齿轮在实际生产中依靠人工实现齿顶倒棱的问题，建立出砂轮中心的中心轨迹和理论轨迹逼近模型，研究各参数对逼近误差的影响从而实现砂轮轨迹的优化，最后实现可行的齿顶倒棱；郭晓东等[5]提出一种螺旋锥齿轮端铣加工刀位的计算方法，通过调整盘铣刀与加工面间的相对位置，以及刀轴矢量的控制，从而实现高效率的齿顶倒棱；魏巍等[6]提出实现高效加工的倒棱方法，该方法基于锥形砂轮，遵循砂轮垂直于弧齿锥齿轮齿面的原则，最终实现端铣加工；卞博等[7]基于建立的齿顶棱线方程推导出刀具轨迹，并经过几何变化计算出刀位点以及刀轴矢量，最后实现精确控制螺旋锥齿轮齿顶倒棱。

在轨迹规划方面，Toumier C等[8]基于等残留高度法进行五轴加工刀具的轨迹规划研究，使加工后的零件表面获得基本一致的残留高度；吴宝海等[9]提出自由曲面五轴数控加工的刀具轨迹规划需要从三维的角度出发，研究出刀具与自由曲面治安的几何啮合关系；樊文刚等[10]指出五轴端铣加工中，刀具轨迹的规划应该尽可能从整体出发，要充分考虑机床的运动学等研究；黄曼曼等[11]提出一种对斜齿轮齿顶线同时进行倒棱的方法，通过计算刀具参数来规划刀具的轨迹；崔雪莹等[12]仅对用于齿廓弧面倒棱的挤棱刀廓形进行了设计，张飞等[13]仅提出了一种基于CAD图形的齿轮齿廓倒棱方法，均未对螺旋锥齿轮的齿廓倒棱进行研究。

结合以上相关的齿顶倒棱研究，本文提出一种适合螺旋锥齿轮小轮的齿廓倒棱加工技术：从螺旋锥齿轮的齿廓线入手，根据球面渐开线的原理获得完整齿廓曲线方程；基于空间坐标转换原理获得刀位点和刀轴矢量，并规划出倒棱加工的轨迹；最后通过实例来验证该轨迹的可行性，达到替代传统的人工倒棱、提高加工效率的目的，实现螺旋锥齿轮齿廓在中低端数控机床上的倒棱。

1 齿廓线方程

1.1 建立齿廓线方程

根据球面渐开线齿面相形成理论[14]，建立如图1所示的球面渐开线数学模型。以基圆锥顶点O作为新建坐标系的原点，以顶点O与 圆心O1之间的连线作为直角坐标系的Z轴，且由O到O1的指向为Z轴的正方向，以圆心O1与 基圆上点K之间的连线作为坐标系的X轴，且方向由圆心O1指 向点K，并根据笛卡尔坐标系确定坐标系的Y轴。

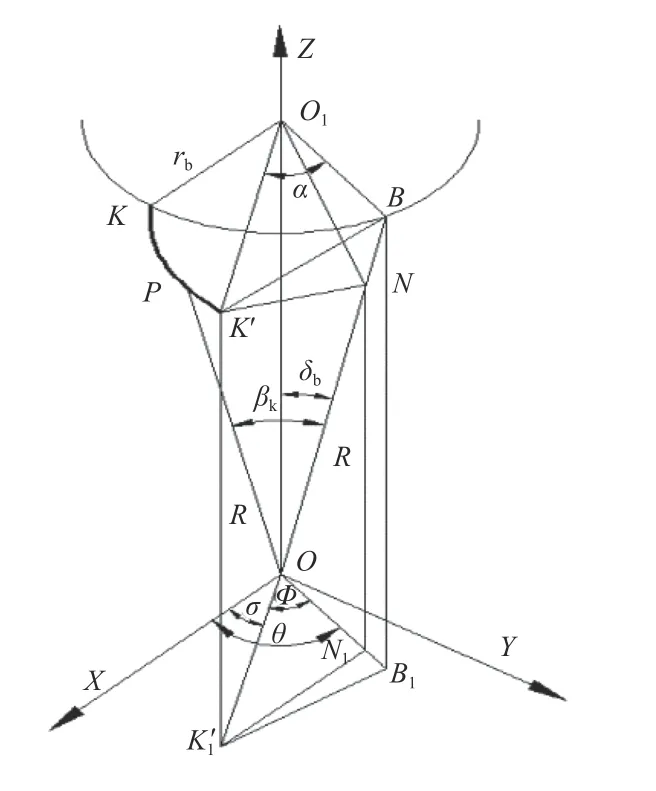
图1 球面渐开线数学模型

由图1可知，球面渐开线位于以点O为圆心、半径为R的球面上，因此可知其参数方程为

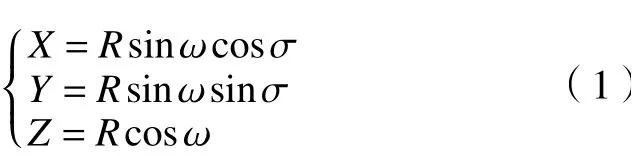
根据球面渐开线数学模型中的几何关系整理出式（2），δb为基锥角，θ为发生面与基锥底圆切点间的展开角，α为压力角，δ为节锥角。

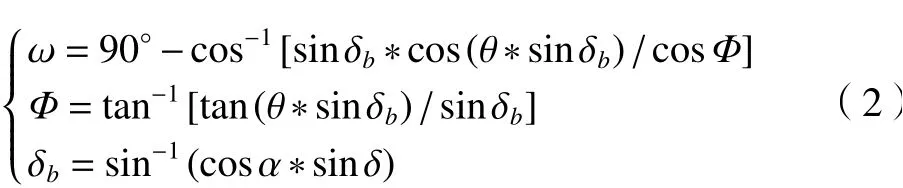
螺旋锥齿轮的一个完整齿廓线包括：齿顶圆弧曲线、工作齿廓曲线、过渡圆弧曲线以及齿根圆弧曲线，且工作齿廓曲线和过渡圆弧曲线均有两条。齿根圆弧曲线和齿顶圆弧曲线分别是上述半径为R球面上齿根圆和齿顶圆的一段圆弧，因此可得

当βa换 为βf、δas换 为δf s、δa换为δf，式（3）即可变成齿根圆弧曲线的参数方程。

过渡圆弧没有具体的参数方程，可以近似为一段平面的圆弧，其圆弧半径rc选取为式（4），rb为基圆半径，r f为齿根圆半径，rm为加工螺旋锥齿轮刀具的最大半径，mn为法面模数。

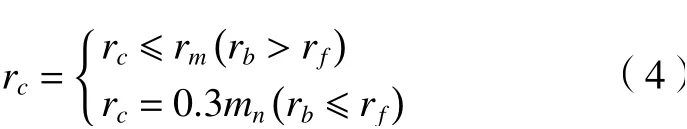
以上为螺旋锥齿轮小轮大端的完整齿廓方程。

1.2 齿廓线方程的验证

以螺旋锥齿轮小轮大端为例以此验证方程，主要参数为：小轮齿数为15，内锥距为30 mm，外锥距为95.295 mm，节锥角为28.18°，齿形角为20°，螺旋角为39°，齿顶高系数为0.7，顶隙系数为0.2。将参数代入1.1节中的小轮大端的齿廓线方程以及王占福[15]构建的球面渐开线模型中推导出的圆锥齿轮球面渐开线方程，绘制的两组齿廓线如图2所示。式（1）～（3）绘制的曲线为图2中实线即理论齿廓曲线，双划线为对比齿廓曲线；由图2c的工作齿廓z轴差值折线可知，在相同的x、y坐标值下，两齿廓线方程上对应z轴的差值在0.063～0.066 mm，可知差值波动范围为0～0.003 mm。这些点分布在整个齿廓线上，由于存在球面半径R以及其他角度参数位数取舍时带来的误差问题，因而对比齿廓曲线和理论齿廓曲线呈现近似平行的状态，可以证明该理论齿廓曲线方程是准确的。

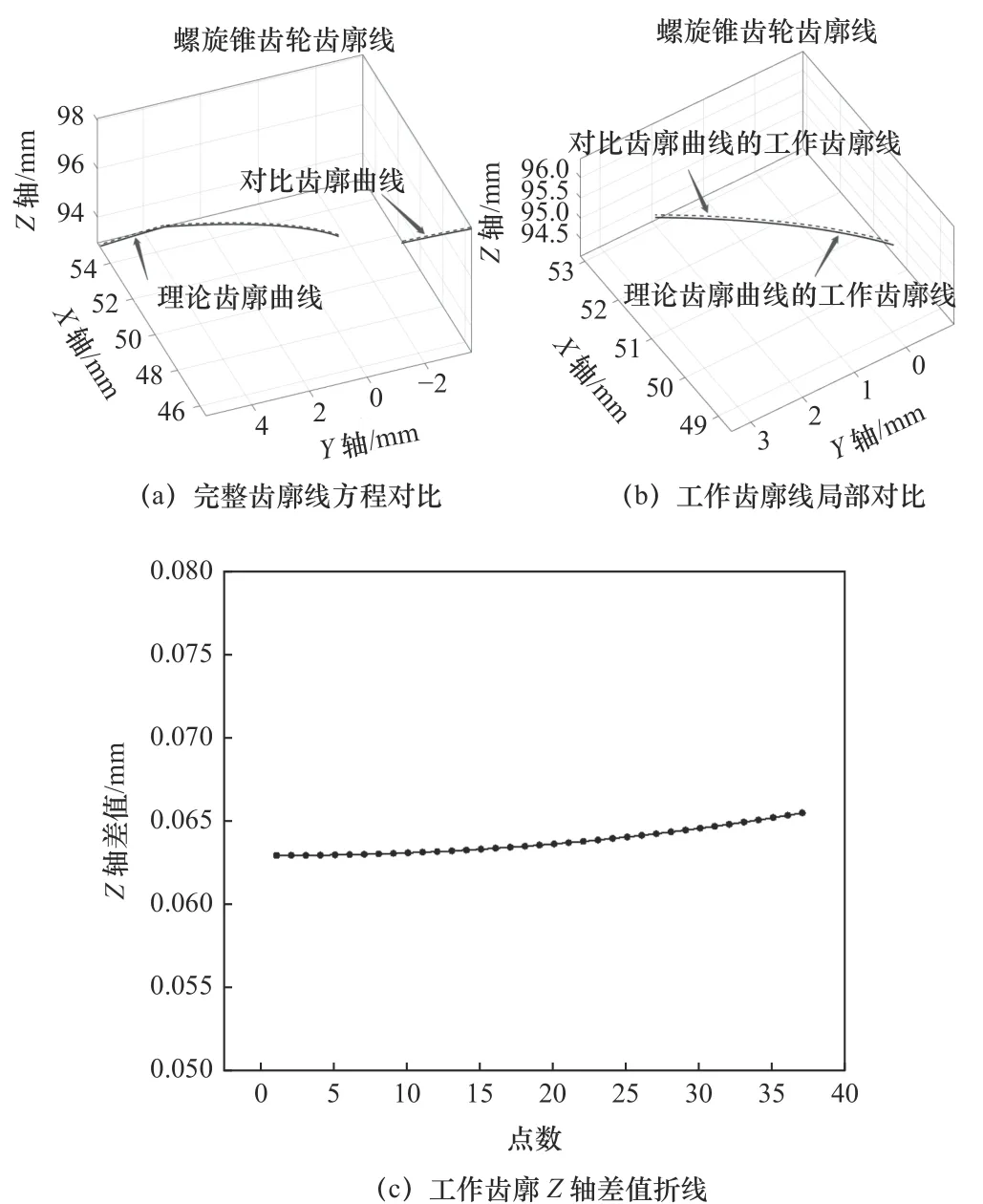
图2 螺旋锥齿轮齿廓线

2 齿廓线目标离散点的获取

根据式（1）～（3）的理论方程，按照等弧长的原则对其进行处理，获得齿顶线、工作廓线以及齿根线上的离散点，过渡圆弧曲线需要近似处理，基圆半径小于齿根圆半径，因此过渡圆弧处的圆弧半径可由式（4）计算得到。

由图2中绘制的齿廓线可知，过渡圆弧处Z轴变化最小，因此等分Z轴，作为过渡圆弧处离散点的Z轴坐标。假设过渡圆弧为平面XOY上的一段圆弧，根据等弧长的原则计算出数据点的X轴和Y轴坐标，最后绘制出所有的离散点，并与理论齿廓线方程对比，如图3所示，图中齿顶线、齿廓线以及齿根线离散点与齿廓线方程基本重合，保证了后续对倒棱轨迹的研究。

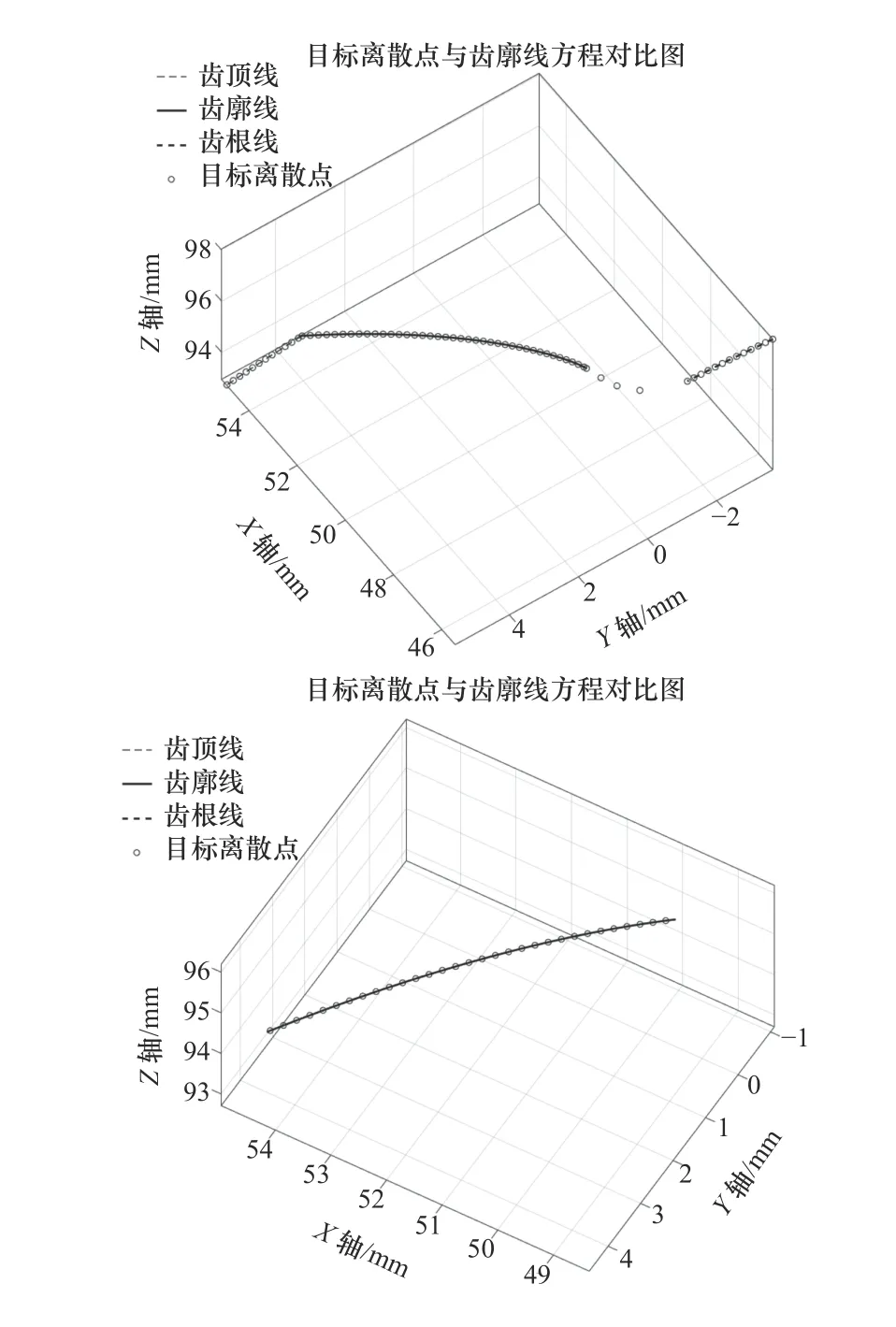
图3 目标离散点与齿廓线方程对比图

3 刀位点和刀轴矢量的计算

3.1 空间坐标转换

建立图4中工件坐标系和刀具坐标系的关系[16]，坐标系S2(O2-X2,Y2,Z2)为工件坐标系，坐标系S3(O3-X3,Y3,Z3)为 刀具坐标系，坐标系S(O-X,Y,Z)与图1球面渐开线数学模型的坐标系一致，建立的坐标系S1(O1-X1,Y1,Z1)是为了方便目标离散点从坐标 系S(O-X,Y,Z)到 工 件 坐 标 系S2(O2-X2,Y2,Z2)之间的转换，L为坐标系S(O-X,Y,Z)与 坐标系S1(O1-X1,Y1,Z1)之间的距离。

图4 工件坐标系与刀具坐标系关系

设坐标系S(O-X,Y,Z)下 某一点的坐标为(x,y,z),转为坐标系S1(O1-X1,Y1,Z1)后 该点的坐标为(x1,y1,z1)，由图4关系可知：

根据图4，假设坐标系S1(O1-X1,Y1,Z1)与工件坐标系S2(O2-X2,Y2,Z2)之 间的Z1轴 与Z2轴的夹角为β，因此X1轴 与X2轴 所夹的锐角为β，设转为工件坐标系S2(O2-X2,Y2,Z2)后 的坐标为(x2,y2,z2)，则由空间坐标转换原理可得：

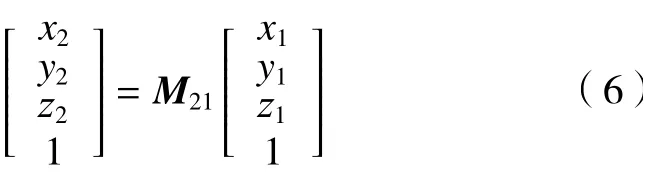
其中，M21为 坐标系S1(O1-X1,Y1,Z1)向工件坐标系S2(O2-X2,Y2,Z2)转换的变化矩阵，且变换矩阵如下。

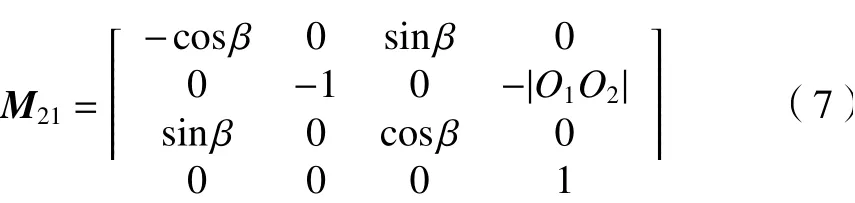
3.2 计算刀位点和刀轴矢量

对于五轴数控机床，工件的端面齿廓一般采用端铣刀和球头铣刀加工，其中，螺旋锥齿轮倒棱加工大多采用锥形铣刀。相较于锥形铣刀，球头铣刀可以降低实际切削半径，适当减小切削加工时的切削功率和切削扭矩；另外，在球头铣刀加工时切入角是连续变化的，不存在突变的现象，此情况下的切削力是一个连续变化的过程，这样可以保证切削状态更加稳定，加工表面光洁度更高，因此选择球头铣刀对齿廓进行倒棱加工[17-18]，并对倒棱的轨迹进行规划[19-20]。

对获取的目标离散点进行空间坐标转换，设坐标系S(O-X,Y,Z)下齿廓线上的某一点的坐标为(x,y,z)，由式（5）～（7）可以计算出工件坐标系S2(O2-X2,Y2,Z2)下 的 坐 标(x2,y2,z2)，并 以 转 换 后 的一些列数据点作为刀具轨迹的刀位点。

球头铣刀对齿廓的倒棱位姿如图5所示，点O表示球头铣刀的刀心点，R表示刀具半径，r表示刀具刃口的半径，且刀具半径与刀具刃口半径相等。L表示螺旋锥齿轮小轮大端处的某一齿廓线，L1表示刀具对齿廓加工时在齿廓上端面的交线，L2表示刀具与齿廓下端面的交线，点P1表示刀具与齿廓线L的交点，点P2表 示刀具与交线L2的交点，点P3表示刀具与交线L1的 交点，点P为齿廓线上的目标离散点。向量n表示球头铣刀的刀轴矢量，起点在刀心点O上 ，且过齿廓线上的目标离散点，点P与点P2沿刀轴矢量间的距离表示刀具切削的深度。

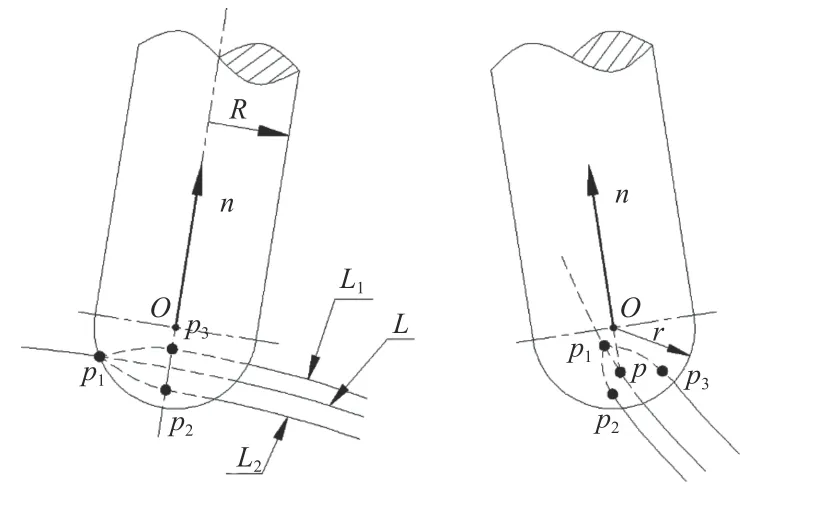
图5 刀具倒棱位姿

由图1中建立的数学模型可知，螺旋锥齿轮齿廓线分布在半径为R的球面上，且球面上任一点的法向量是唯一的，因此不会出现球头刀具与工件的干涉问题。设齿廓线所在的球面方程为

则齿廓线方程在点(x,y,z)的单位方向矢量可以表示为

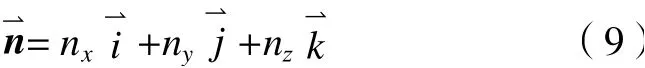
故单位方向矢量中各个分量nx、ny、n z表示为

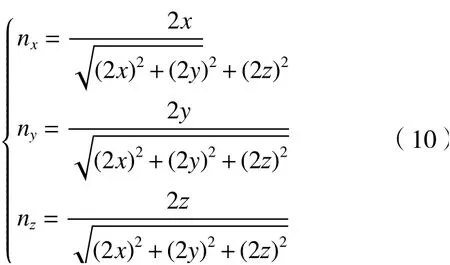
工件坐标系下的刀轴矢量可由向量n来表示，且刀轴矢量与Z轴的夹角如图6所示，锐角ϕ即为刀轴矢量与坐标系Z轴之间的夹角，点p为齿廓线上的目标离散点，由图6的关系可以计算出式（11），即图4中刀具坐标系下Y3轴与工件坐标系下Y2轴之间所夹的锐角。

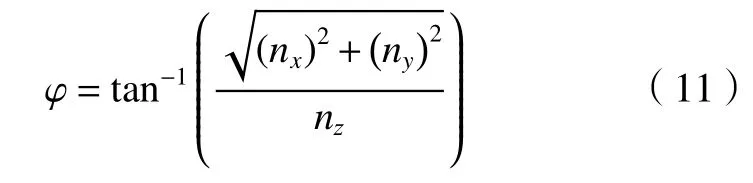
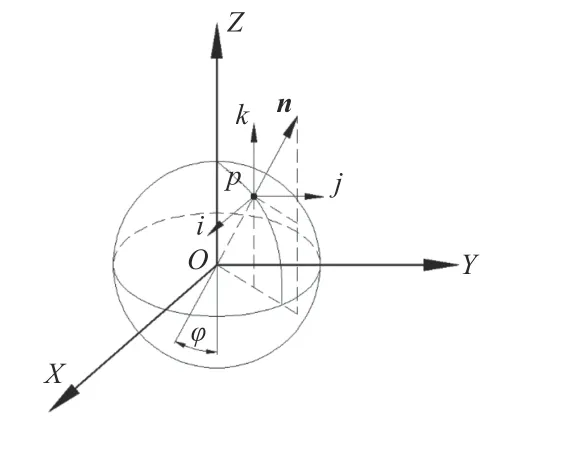
图6 刀轴矢量的夹角

4 倒棱轨迹的仿真

为了验证本文中螺旋锥齿轮齿廓倒棱轨迹规划的有效性，现以验证齿廓线方程的小轮大端参数为例进行球头铣刀倒棱轨迹的仿真。

4.1 MATLAB软件中倒棱轨迹的仿真

首先对获取的目标离散点进行坐标转换，由式（5）～（7）可以计算出工件坐标系下的数据点，获得刀具轨迹。由式（8）～（10）计算球头刀具的刀轴矢量，并经式（5）～（7）转换为工件坐标系下的刀轴矢量，如图7所示。

图7中采用基于积累弦长法的NURBS曲线插补对刀具的倒棱轨迹进行仿真，根据目标离散点计算出控制顶点，选取权重因子后最后实线绘制出齿廓线轨迹，基于该插补算法可以最大限度地绘制出齿廓线过渡圆弧处的轨迹，图中轨迹线上各离散点的箭头即为球头刀具的刀轴矢量，保证每一点处的方向唯一。

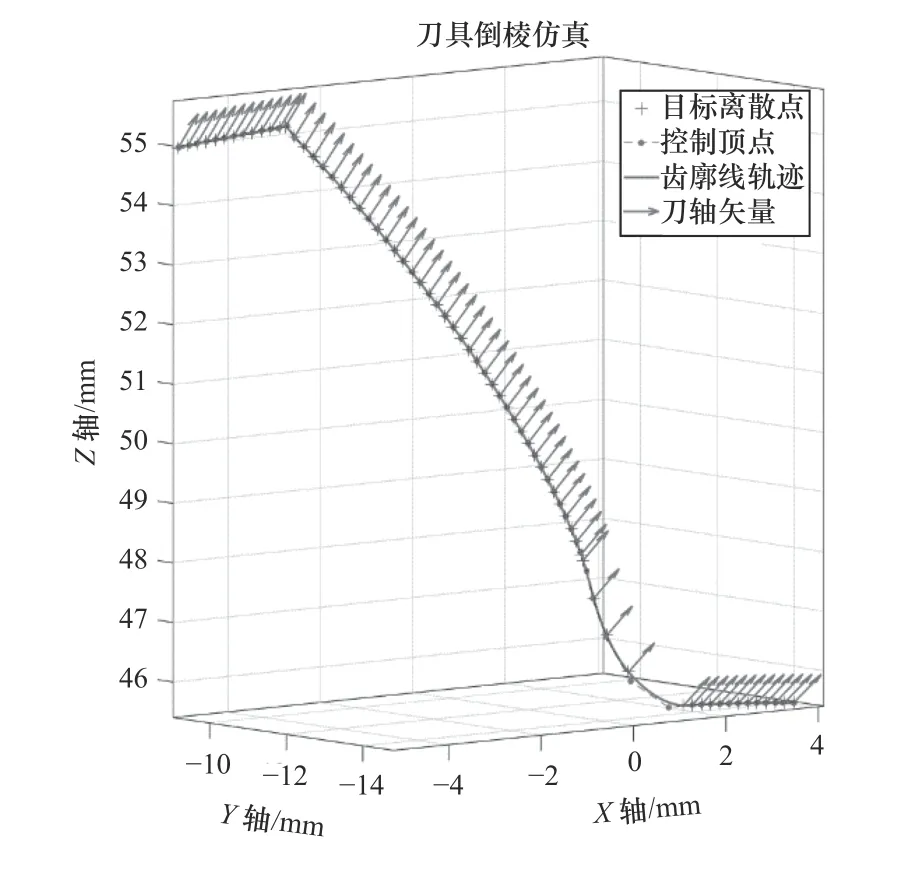
图7 刀具倒棱仿真

4.2 VERICUT软件中倒棱轨迹的仿真

在VERICUT软件中进行螺旋锥齿轮模型小轮大端的倒棱仿真，模型参数与前面一致。首先添加SINUMERIK 840D作为数控控制系统，根据五轴数控机床各轴的实际关系定义X、Y、Z等轴，设置工件坐标系与刀具坐标系之间的位置，在“Stock”中导入工件模型文件，在加工刀具处添加球头刀具，并设置刀具必要的参数，最后添加已经编写好的数控程序，模型倒棱仿真如图8所示。

图8 模型倒棱仿真

图8中球头刀具的刀轴矢量可由公式（10）计算出各值的大小，方向设置表示为数控程序中的A轴，且由图4中刀具坐标系与工件坐标系之间的关系可知A=-φ。

图9为模型在不同深度下切削后的对比图，刀具在模型上加工出一个内凹槽；切削深度为0.1 mm和0.2 mm时，球头刀具加工过的齿廓线处明显不平整，加工效果差；切削深度为0.3 mm和0.4 mm时，加工留下的曲面相对均匀，加工效果明显更好，但当加工深度不断增大时会导致齿廓处切削过大，给工件的啮合产生不好的影响，降低使用寿命。

图9 模型切削对比

5 结语

本文研究了基于球头刀的螺旋锥齿轮齿廓倒棱轨迹规划，基于空间坐标转换以及球头刀倒棱时与工件的位姿关系，计算出了齿廓倒棱轨迹，最后在MATLAB和VERICUT软件上进行倒棱仿真，得出以下结论：

（1）根据球面渐开线模型计算出的完整齿廓线方程，经对比分析验证了方程的准确性。

（2）获得的齿廓线目标离散点，根据空间变换矩阵及设计的刀具倒棱位姿关系，成功计算出倒棱轨迹的刀位点和刀轴矢量。

（3）倒棱加工可以按照计算出的齿廓倒棱轨迹进行，且加工表面相对均匀。

（4）利用该方法可以对螺旋锥齿轮小轮大端和小端进行倒棱，补足了国内螺旋锥齿轮在中低端数控机床上的倒棱，可以替代人工倒棱从而提高加工效率。