基于改进粒子群算法的六自由度工业机器人轨迹规划＊

苏 俊 熊瑞平 温记明 李云秋 谭 平

（四川大学机械工程学院，四川成都 610041）

伴随着中国从制造业大国迈向制造业强国的产业升级趋势，工业机器人在大批量生产中被越来越多的使用[1]。在本文工况中，待处理工件有4处位置点需要进行去毛刺打磨操作，考虑到工件的大批量处理，因此设计使用工业机器人进行去毛刺打磨处理操作并规划机器人运动轨迹，使得机器人运动平稳且运行时间最短，从而提高工件打磨效率。机器人路径规划算法是工业机器人技术的重要组成部分，常用的机器人运动轨迹规划优化目标有运动时间最优、能量最优以及混合最优目标等优化目标[2]。本文以时间最优作为优化目标，通过优化轨迹路径参数使得轨迹运动时间最短[3-7]。

常用的规划轨迹有样条轨迹、多项式轨迹和分段轨迹等方式[8-9]。其中样条曲线轨迹求解相对复杂[10-11]，多项式轨迹常用三次、五次、七次多项式进行轨迹优化，三次多项式曲线求解简单但加速度不连续，沿规划路径运动不平稳[12]；单条5次多项式轨迹能够保证运动的稳定性，但其适应能力较差，容易因为一两个点造成整个曲线的变形[13]；高阶的7次规划曲线，求解较复杂且会出现龙格现象，其求解出的值准确度更低[14]。本文选取3次-5次-3次三段多项式轨迹方法，该曲线在保证规划曲线位移、速度和加速度连续，机器人运行平稳的同时，通过3段方程提高了轨迹对中间点位的适应能力，避免受限于中间点造成轨迹扭曲的问题，提高了轨迹过度点平滑性[15]；同时约束方程最高求解次数为5次，保留了多项式轨迹计算简单的优势。常用的轨迹优化方法有粒子群算法、蚁群算法和遗传算法等。本文引入粒子群算法进行轨迹优化，粒子群算法成熟度高、求解能力强。但是，粒子群算法的缺点是算法较早熟，容易过早陷入局部最优。因此，本文通过融合免疫操作的方法对粒子群算法进行改进，增强粒子群算法的搜索能力，通过改进后的粒子群算法提高机器人运行效率；并利用本文的轨迹规划问题，将融合免疫操作的改进粒子群算法与传统粒子群算法、传统可变参数改进粒子群算法进行对比，考察本文算法的性能。

本文研究利用工业机器人进行工件去毛刺打磨工作，针对机器人在笛卡尔空间中的4个位姿点位进行轨迹规划，减少工作时间，提高工件处理效率。

1 运动学建模与分析

待处理工件为异型梯形工件，需要对4个柱体端面进行去毛刺打磨，如图1所示。

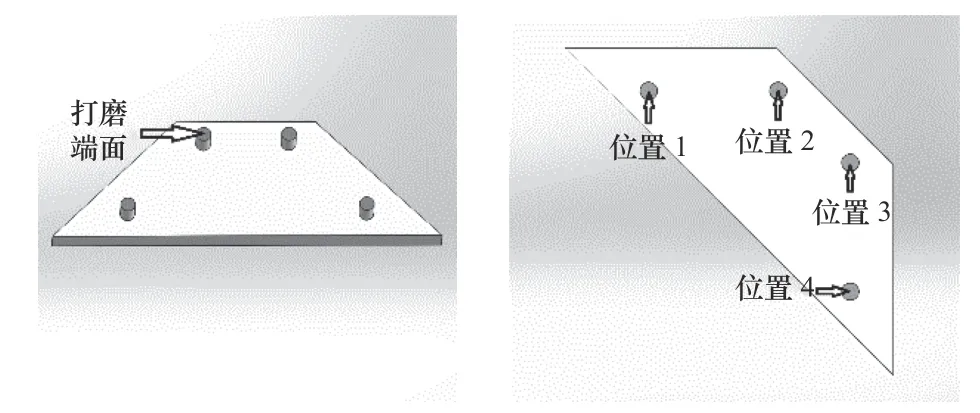
图1 打磨处理位置

4个打磨位姿点放置在机器人空间坐标系中，分布如表1所示。

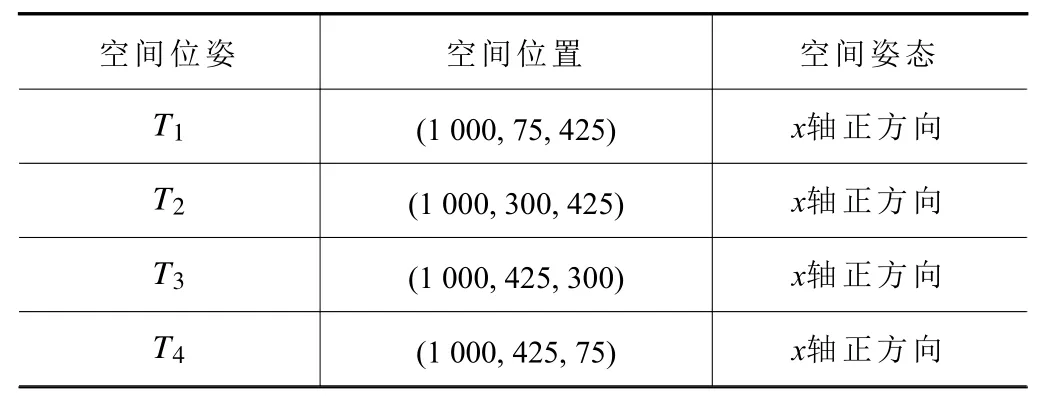
表1 目标点末端位姿

其中Ti表示第i点的空间位姿。本文引入库卡KR16-2型工业机器人进行去毛刺打磨操作，其改进DH参数如表2所示。

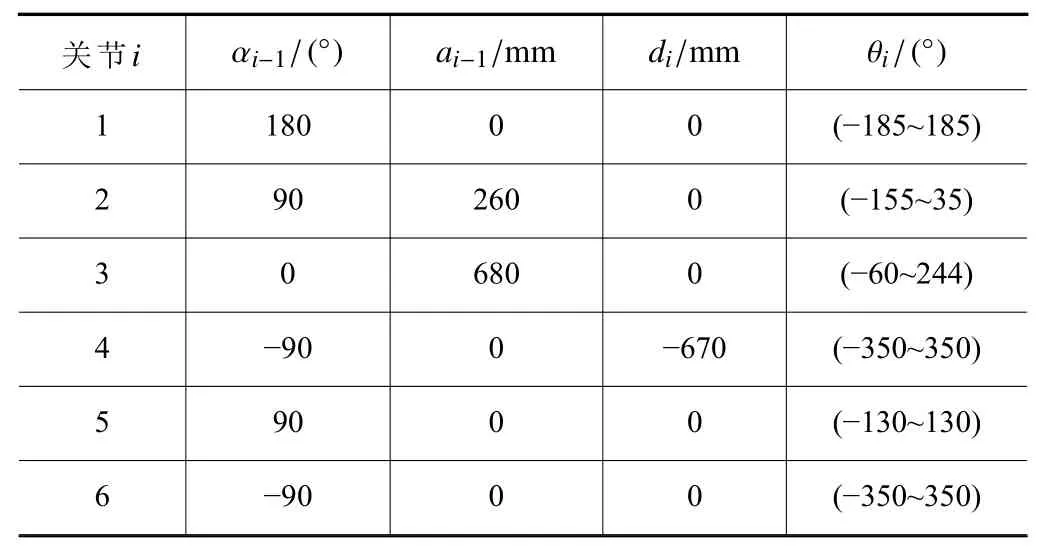
表2 机器人改进D-H参数

其中，i表示机器人第i轴 、αi表示连杆扭转角、ai表示连杆长度、θi表 示关节转角、di表示连杆偏移距离。为确定机器人的运动范围是否满足工况需求，使用蒙特卡洛法[16]计算机器人的工作空间，利用Matlab开源机器人运动学工具箱Robot Tool Box[17]进行运动学建模仿真验证。算法代入大量随机点近似遍历机器人运动空间，仿真得到机器人工作空间范围。代入5 000组随机角度值计算机器人工作空间范围，保留运算结果数据，输出点位分布如图2所示。

图2 机器人工作空间范围

机器人工作空间近似为一个高度值范围[-1 000,1 400]mm ，半径1 600 mm的椭球体空间，包含4个目标位置点位，符合工况需求。利用机器人学工具箱求解笛卡尔空间位姿对应的关节空间逆解，结 果如表3所示，其中Pi表 示第i点的关节角弧度值。

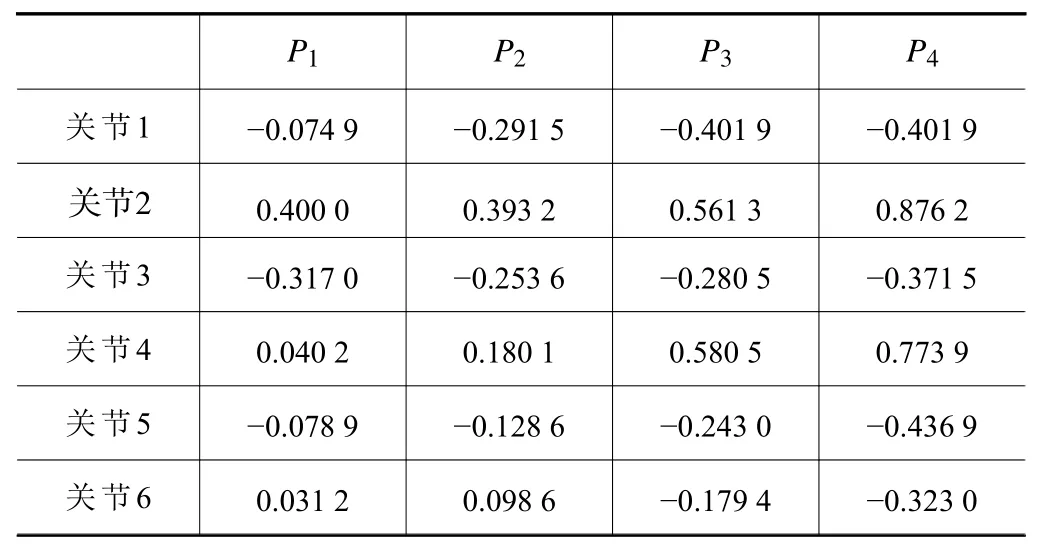
表3 关节空间逆解结果rad

2 机器人轨迹规划

针对机器人关节空间轨迹规划，使用3-5-3三段多项式曲线进行轨迹规划，在保证曲线连续、速度和加速度连续的基础上利用3段分段轨迹增强轨迹对位姿点位的适应能力。设3段曲线角度为q1～q3，曲线参数aij表 示第i段曲线第j个参数，3段运动时间参数分别为t1～t3，可得到关节空间中轨迹位置关系满足函数关系式（1），轨迹速度方程满足函数关系式（2），轨迹加速度方程满足函数关系式（3）。

设关节空间中4个目标点转角位置分别为Q1～Q4，为保证机器人运动轨迹平滑稳定无冲击，根据分段轨迹约束条件，初始点Q1和 终点Q4满足速度和加速度为0，路径点之间的位置、速度及加速度连续，3段轨迹运行时间分别是tl1～tl3，约束表达式分别有位置连续约束方程（4）、速度连续约束方程（5）和加速度连续约束方程（6）。

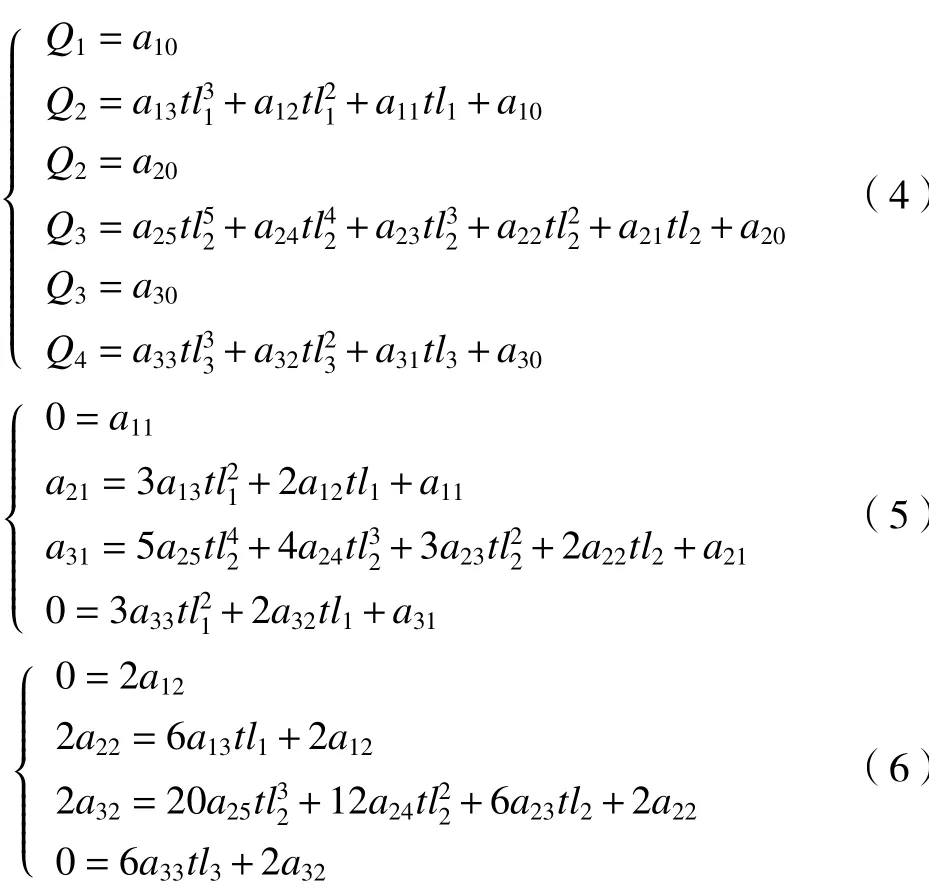
将上述约束方程组写作q=a×A，其中q为包含路径点Q1～Q4的向量，a包含曲线参数aij的运动方程系数，A为包含运动时间t1～t3的方阵。公式变形为a=q×A-1，求解轨迹方程系数aij，即为最优状态下的轨迹曲线方程。

3 融合免疫操作的改进粒子群算法

本文的轨迹优化目标为机器人运行时间最优，即在满足轨迹约束条件下机器人沿轨迹运行时间最短。3-5-3多项式轨迹由3段轨迹组成，总运行时间即为3段之和，即tl=tl1+tl2+tl3，使用智能算法对轨迹的14个参数（aij）同时进行优化，使得机器人沿轨迹运行时间值最少。同时每一机器人关节有运行速度与加速度限制，得到优化目标函数表达式（7），其中目标函数f(tl)表示3段时间之和最小，限制条件为运行角速度ω值小于等于限制速度ωmax，运行角加速度α值小于等于角加速度限制 αmax。

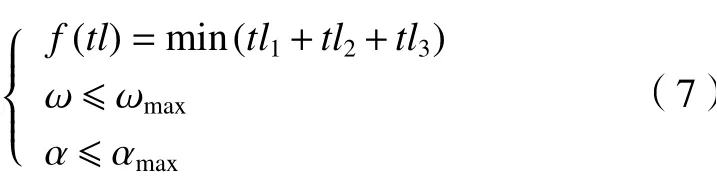
粒子群算法是上世纪90年代提出的一种智能优化算法，通过多个粒子迭代探索最值问题的最优解[18]，其表达式如式（8）。

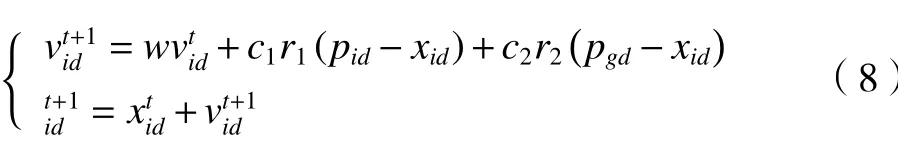
式中：i表示当前种群中某一粒子，t表示粒子迭代次数，d表示粒子维度；表示粒子位置值，表示粒子速度；pid表示当前粒子在迭代中的历史最优位置；pgd表示全局最优位置；步长ω和学习因子c1和c2是分布在[0～1]之间的随机数。为适应本文的优化目标，粒子位置xid的3个维度分别设置为3段轨迹的运行时间tl1～tl3，建立粒子群适应度公式如式（9）。

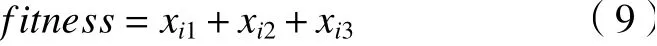
粒子群算法计算简单、运算效率高，一经问世便被应用在各个领域。但是粒子群算法容易早熟，过早进入局部最优，往往难以求出更优秀的全局解[19-20]。改善粒子群算法早熟缺陷的常用方式是引入可变参数，例如线性递减参数法、自适应权重法、随机参数权重法等；可变参数法在早期降低学习因子c1和c2的值，提高步长ω的值，在早期提高算法的全局搜索能力，在后期提高算法局部搜索能力，优化算法在整体和局部的搜索能力[21-22]。参数因子设计公式如式（10）。

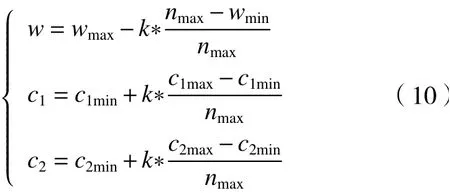
通过引入可变参数的粒子群算法，能够在一定程度上改善粒子群算法容易陷入局部最优的问题，但可变参数法全局探索能力仍然限制较大、效果不够好[23]。

为了更好地改进粒子群算法，提高轨迹规划能力，本节通过融合免疫算法的操作对粒子群算法进行改进。免疫算法参考生物的免疫系统，其核心概念是抗体多样性、免疫记忆与免疫接种[24]。在运用免疫算法进行问题求解时，抗原代表了满足约束关系的最优解，抗体为当前候选解。抗体与抗原之间的亲和力值反映了当前解的优秀程度，抗体和抗体之间的亲和力反映了候选解的多样性。免疫记忆反应指从记忆库中搜索该类问题的较优解记忆粒子作为抗体，模拟与抗原最优解反应所产生的抗体值。免疫接种模拟了接种疫苗治疗相应病症的手段，通过有指导、有目的地对种群粒子进行修改，从而提高种群粒子多样性、抑制优化过程中的退化效应，提高算法搜索性能[25]。免疫算法操作依赖的计算参数有浓度、浓度选择概率、适应度概率、和免疫替换概率等。粒子浓度计算如式（11），其中xi表示粒子i，D(xi)表示粒子i的抗体浓度，N表示种群数量，f(xi)表 示粒子i适应度函数值。

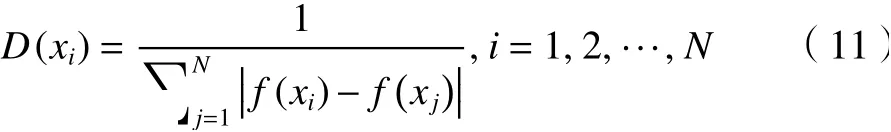
推导出粒子浓度概率公式（12），其中PD(xi)表示粒子i浓度概率值。

粒子i适应度概率计算式为式（13），其中PF(xi)表 示粒子适应度概率，psum表示个体最优适应度值。

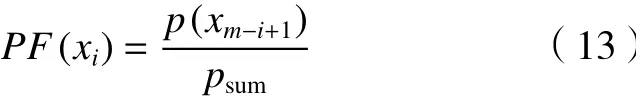
免疫替换概率计算式为式（14），表明当前粒子多大程度上需要进行替换操作,rand为范围在[0-1]的随机数。PR(i)表 示粒子i的免疫替换概率。

免疫替换生成公式为式（15），其中rang为设置的范围设定值。当免疫替换概率值PRi超过设定值，则进行免疫替换操作。

本文在基本粒子群算法的基础上进一步引入免疫操作，利用免疫算法的浓度挑选机制，抑制近似的高浓度解，促进边缘的低浓度解，同时通过免疫接种操作对种群进行有指导、有目的地替换，提高种群多样性，从而提高改进粒子群算法的搜索能力。这一算法流程图如图3所示。

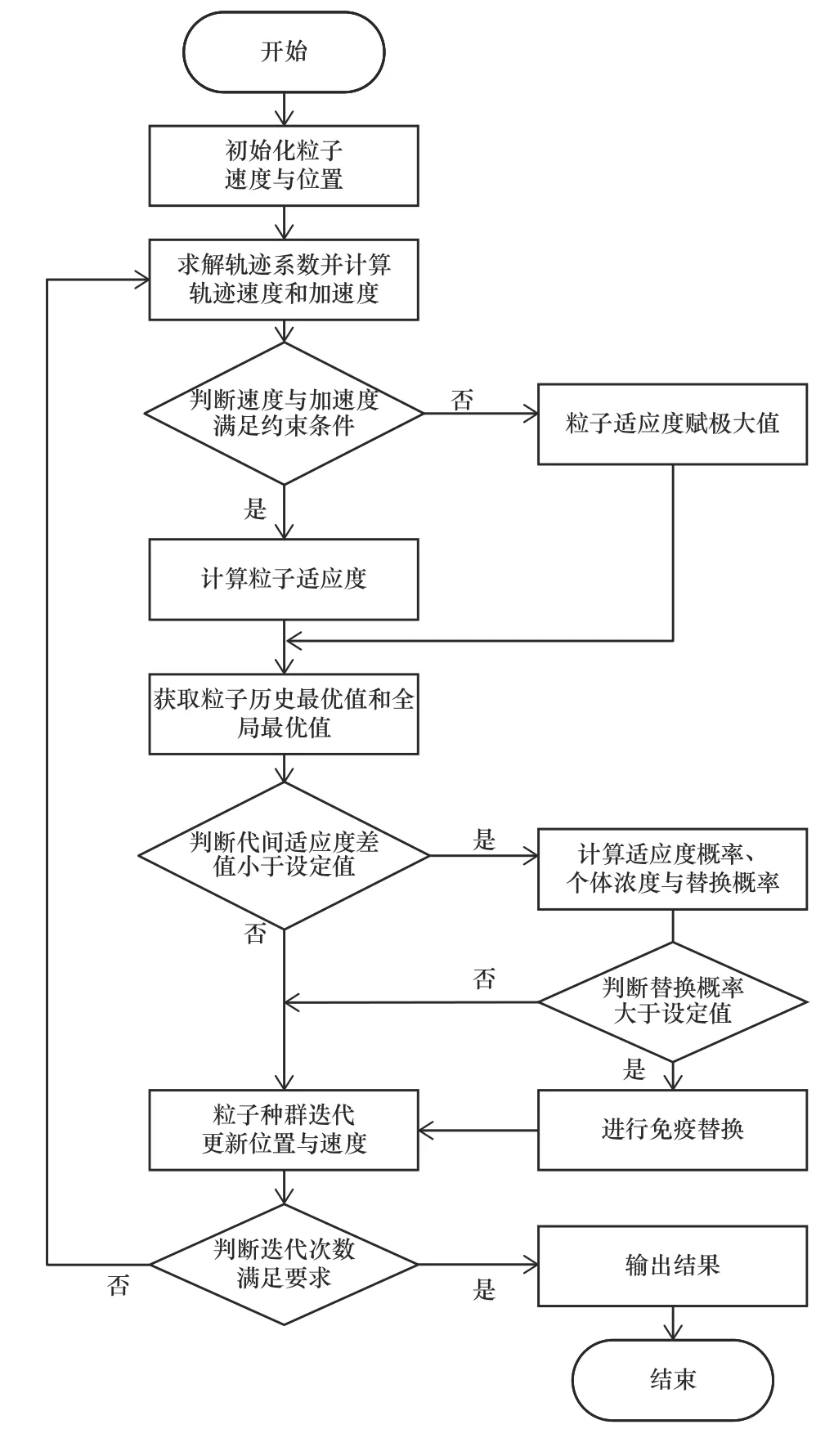
图3 算法流程图

应用改进粒子群算法对机械臂进行3-5-3分段轨迹规划，算法主要流程步骤为：

Step1在粒子搜索空间中随机生成N个粒子，初始化粒子位置与速度。

Step2求解粒子对应的轨迹系数，计算当前轨迹角速度与角加速度大小。若角速度和角加速度超过设定值，表明粒子不满足角速度和角加速度限制要求，将其适应度值设置为极大值常数C。若角速度与角加速度满足限制要求，计算粒子适应度值。

Step3计算粒子历史最优值pid和全局最优值pgd。

Step4计算两代间最优适应度差值是否小于设定值di f，若两代间适应度差值小于设定值，则表明搜索算法陷入局部最优，全局搜索能力较弱，此时进行免疫操作。首先计算种群粒子浓度概率、适应度概率、免疫替换概率，若免疫替换概率大于设定值则对种群粒子进行免疫替换操作。

Step5利用粒子群算法对种群进行迭代，更新粒子位置与速度。

Step6判断迭代次数是否满足设定值，若满足设定次数则输出结果，算法结束；若还未满足迭代次数，则返回Step2循环算法。

4 仿真实验

为考察改进后算法的性能，选取算法测试函数对算法性能进行考察，对比传统粒子群、传统变参数改进粒子群和本文提出的免疫粒子群3种算法的性能，以衡量新算法的改进效果。本文选取Griewank function、Ackley function、Schaffer2 function和Levy function这4种主流的具有多局部最小值，求解难度较大的测试函数。4种测试函数全局最小值均为0，实验以测试函数函数值作为适应度进行迭代计算。设置粒子群种群个体数为N=20，总迭代次数设置为K=100。对于传统粒子群算法，步进参数ω 设置为0.5，学习因子c1和c2设置为 0.35；对于可变参数改进粒子群算法，步进参数ω设置最大值 ωmax=0.9，最小值ωmin=0.2，学习因子c1和c2最大值设置为c1max=c2max=0.5，最小值设置为c1min=c2min=0.2。对于融合免疫操作的改进粒子群算法，代间适应度差值阈值di f设置为di f=0.05，免疫替代概率Prep设置为Prep=0.01，免疫粒子生成范围参数rang设 置为rang=1。对每一测试函数分别使用3种算法重复100组求解实验，每一组总迭代次数设置为100代，同时计算第10代、20代、50代、100代平均适应度值，实验结果如表4所示。

分析表4的实验结果，本文所提出的融合免疫操作的改进粒子群算法在4种主流测试函数中，相较于传统粒子群算法和传统改进粒子群算法均体现出了较大的优势。在第100代适应度结果中，除在Griewank function测试函数中免疫粒子群算法适应度降为改进粒子群算法一半以外，其他3种测试函数中免疫粒子群算法适应度值相较于其他两种传统求解算法均小于1个数量级以上，特别是在Schaffer2 function测试中小于5个数量级，体现了免疫粒子群算法求解能力的优势。同时在第10代、20代、50代中，免疫粒子群算法适应度值均小于其他两种传统算法，且适应度降低速度更快，体现了免疫粒子群算法迭代能力的优势。对比表格数据，可以得出本文所提出的融合免疫操作的改进粒子群算法在迭代求解能力、求解结果上均优于传统粒子群算法及传统改进粒子群算法。

表4 测试函数适应度均值

在考察本文所提出的算法对于主流测试函数求解性能后，为了进一步对比验证改进后的算法在处理本文轨迹规划问题上的性能，本文利用传统粒子群算法、基于变参数的改进粒子群算法和融合免疫操作的改进粒子群算法对机器人6轴进行最短时间轨迹规划求解运算，并进行适应度结果对比。设定机器人各轴角速度限制设置为 ωmax≤2.88 rad/s2，角加速度限制设置为αmax≤45.45 rad/s2，计算各轴适应度曲线。如图4所示，分别计算基本粒子群方法（方法1）、可变参数改进粒子群方法（方法2）和本文提出的融合免疫操作的改进粒子群方法（方法3）3种方案的各轴适应度迭代值。如表5所示，计算机械臂6个轴迭代100次适应度最终值f1～f6，6个轴适应度均值fave和六轴适应度最大值fmax。如表6所示，对比1表示方法2相较于方法1在适应度上的改进效果，对比2表示方法3相较于方法1在适应度上的改进效果，对比3表示方法3相较于方法2在适应度上的改进效果。s1～s6表示机器人6根轴的适应度优化率，save表示平均适应度优化率，smax表示最大适应度优化率。从适应度迭代结果来看，相较于传统粒子群算法，可变参数改进粒子群算法在机器人路径规划问题中的适应度平均改进1.4倍，最大值适应度改进1.522倍；而本文所提出的融合免疫操作的粒子群算法相较于传统粒子群算法在平均适应度上改进3倍，最大值适应度改进2.831倍。根据图表结果，本文所提出的融合免疫操作的改进粒子群算法在路径规划问题中相较于传统粒子群算法和传统改进粒子群算法迭代效率更高，适应度优化更快，适应度结果更优秀。

表5 适应度值

表6 适应度优化率

图4 机械臂适应度曲线

在前述最大适应度规划条件下，进行机器人各轴路径规划如图5所示，得到3种不同算法方案下机械臂6个轴的角位移、角速度、角加速度曲线。其中图5a～c分别表示方法1、方法2和方法3的角位移曲线，角位移运算终值一致，3种方法均完成了路径规划，机械臂抵达指定位置；图5d～f分别表示方法1、方法2和方法3的角速度曲线，3个图中各轴角速度最大值均满足最大角速度2.88 rad/s限制；图5g～i分别表示方法1、方法2和方法3的角加速度曲线，3个图中各轴角加速度最大值均满足最大角加速度最大值均满足最大角加速度45.45 rad/s2限制。机械臂规划轨迹平滑，各轴运动角速度、角加速度连续且满足最大运行角速度和角加速限制条件。

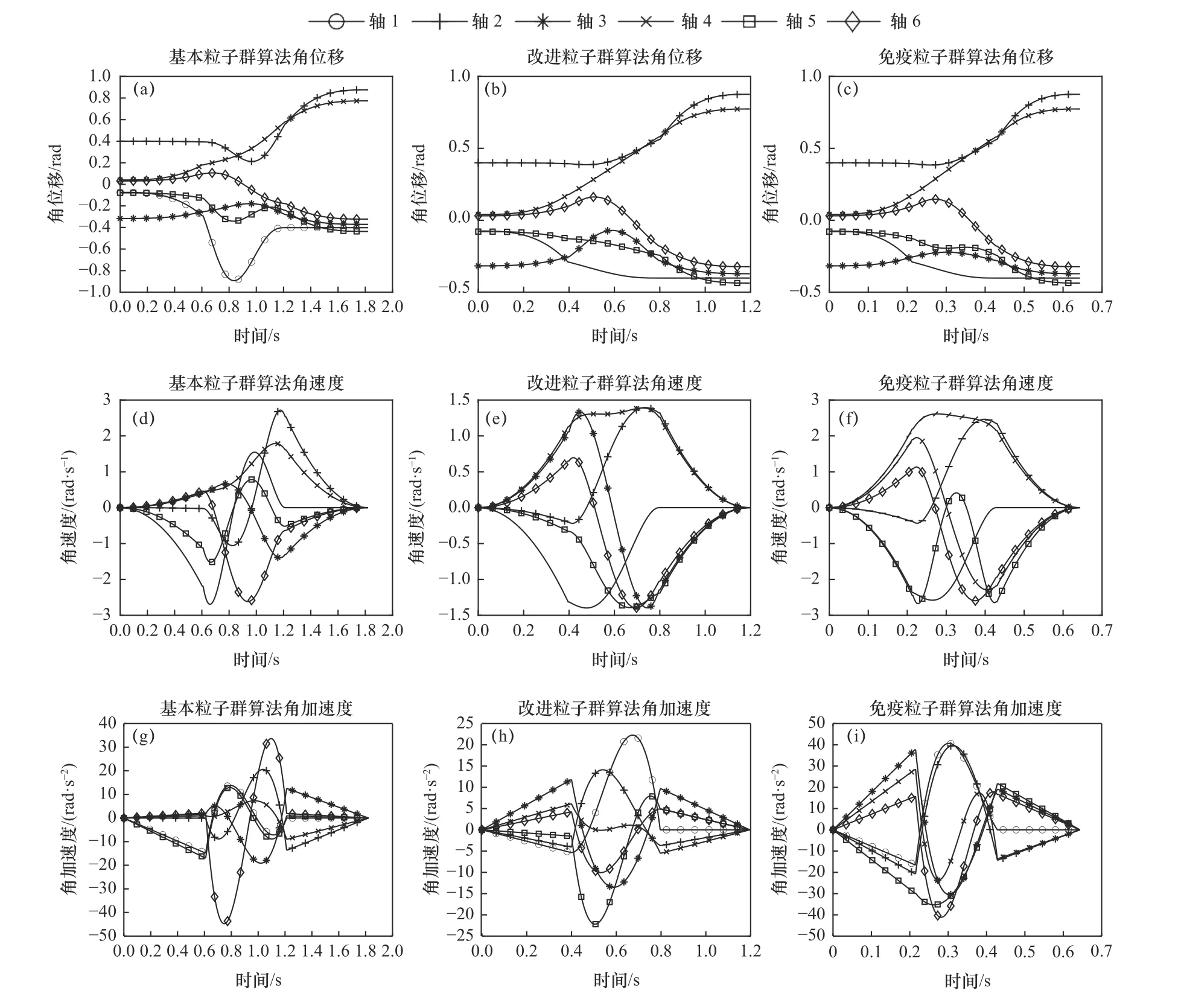
图5 机械臂路径规划曲线

5 结语

本文为解决机械臂路径规划最短时间问题，提出了融合免疫操作的改进粒子群算法以改善传统粒子群算法易陷入局部最优的问题，使用此算法与传统粒子群算法和传统可变参数改进粒子群算法在最短时间问题上进行求解对比。所提出的改进算法相较于传统粒子群算法适应度更佳、收敛更快，大大改善了传统粒子群算法易于早熟、容易陷入局部最优的劣势，缩短了机械臂路径规划时间。

综上所述，本文建立机器人运动学模型，利用分段多项式曲线进行轨迹规划，通过融合免疫算法操作改进传统粒子群算法，控制机器人动作，实现机器人轨迹控制，提高机器人工作效率，为工业机器人的空间轨迹规划提供了一套思路方法。