工业机器人伺服传动系统对整机性能影响研究＊

窦文娟 龚 伟 王小平 吴曾萍 李本旺 黄云峰

（①中国汽车工程研究院股份有限公司，重庆 401122；②成都飞机工业(集团)有限责任公司，四川成都 610073；③重庆凯瑞机器人技术有限公司，重庆 400799；④重庆大学机械传动国家重点实验室,重庆 400044）

工业机器人技术水平是衡量一个国家制造业水平和核心竞争力的重要标志[1]，然而目前整机性能检测的核心技术、测试设备仍掌握在瑞士、德国和日本等工业强国手中[2-3]。我国参考标准仅对机器人末端精度和通用安全进行规范，没有涉及双臂、移动和复合型机器人等特种机器人的性能参数指标，造成测评方式针对性不强、整机性能影响机理与评估方法缺失等问题，从而导致难以全面真实地反映整机性能。探索机器人核心部件及其组合驱动系统的性能，揭示核心部件对整机性能的影响机理[4]，是开展整机性能测评的基础。（1）研究减速器、伺服电机及控制器等核心部件的静动态特性、寿命测试方法和性能退化评估方法与测试技术。（2）研究工业机器人伺服传动系统多物理过程、多参数和多维机电耦合关系，建立动力学运行品质模型。（3）提出核心部件及其组合系统参数-整机性能测试方案，验证核心部件之间机电耦合因素对整机性能的影响机理。

工业机器人技术是一个多学科、多领域高度交叉集成的技术高地。工业机器人核心部件是支撑机器人技术向高端智能化发展的重要基础，其性能和质量直接影响对整机性能的可靠性评估[5]。评估工业机器人核心部件的性能参数及性能退化机理，建立一套完善的分析、测试及评价方法，对于研究核心部件对整机性能影响具有重要意义。

1 伺服传动系统机电耦合模型

伺服传动系统是一个多输入、多输出、非线性和强耦合的系统[6-7]，需要建立伺服-传动系统机电耦合模型分别研究各个子系统，再分析系统整体静动态特性参数对该系统运行品质的影响规律，并构建伺服传动系统运行品质模型。研究机器人核心部件（减速器、伺服电机）静动态特性，提出性能退化模型概念，通过仿真和试验验证伺服传动系统对整机性能的影响机理。

1.1 动力学模型

以高性能机器人常用的永磁同步电机为研究对象，通过运动学和动力学模型给定机器人驱动电机角度和负载计算系统响应，在旋转坐标系下建立数学模型。永磁同步电机电压方程和电磁转矩方程为[8-9]

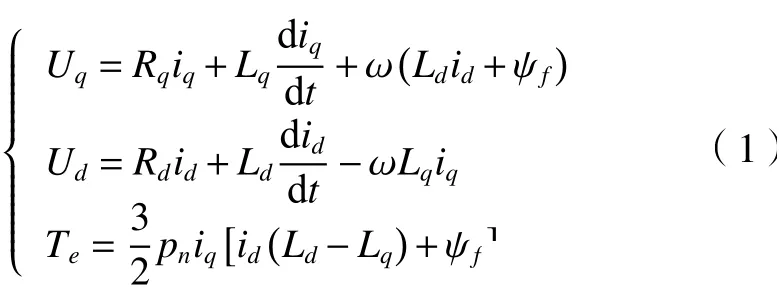
电机的机械运动方程为

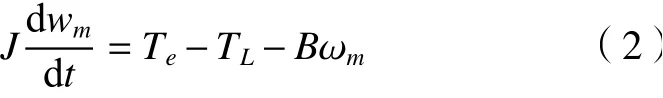
式中：J为电机转子轴转动惯量；ωm为电机输出轴机械转速；Te为永磁同步电机输出力矩；TL为负载力矩；B为电机阻尼系数。

伺服电机矢量控制原理模型如图1[10]。

图1 伺服电机矢量控制原理

永磁同步电机矢量控制原理[11]（以双闭环结构永磁同步电机的矢量控制为例）：外环为速度环，输入为电机转速参考值与电机反馈值的差值。反馈通过电机后端的光电编码器输出角位移和角速度，速度的差值经过转速环控制器后输出电流参考值，与反馈电流的差值输入到电流环控制器，电流的反馈值通过电机内部的霍尔传感器检测。外环为电流环，其响应速度最快，输出两相电压的参考值，两相电压经过逆变器输出三相电压到伺服电机。

基于传递函数和典型I、典型II系统[12]，以工程实践经验法，简化伺服电机3个控制器的参数以此搭建Clark变换和Park变换模型，最终得到控制仿真模型如图2。

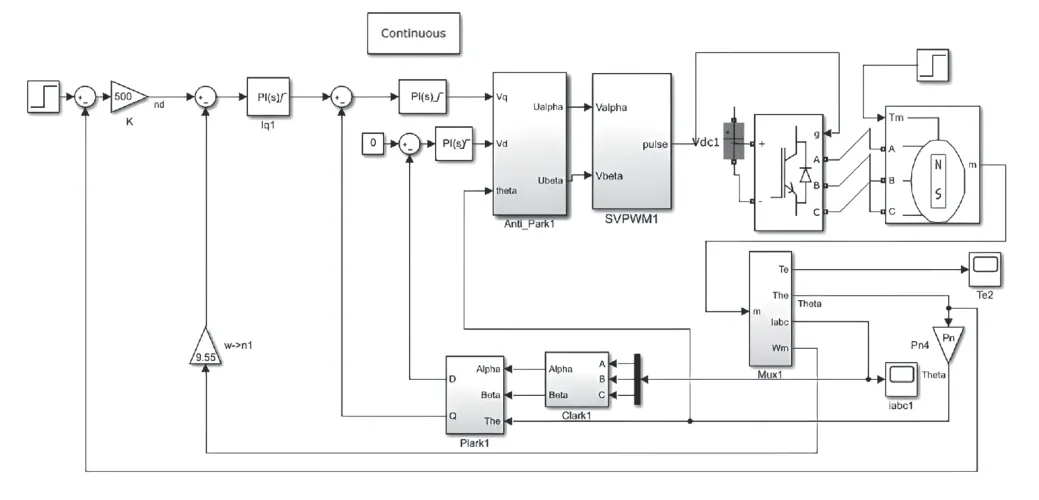
图2 伺服电机矢量控制仿真

整定伺服电机的三环PID参数，在Simulink环境下进行双闭环伺服电机的空载及加载仿真，矢量控制模型和仿真完全吻合，说明建模和参数的选取满足要求。

伺服传动系统机械传动部分采用集中质量建模，驱动系统通过矢量控制建模，忽略齿轮箱的内部结构，联立机械传动与电气驱动部分，得到伺服电机-减速器-负载的机电耦合动力学模型[13]。采用三质量两轴模型简化减速器的内部结构如图3，并根据力学运动方程得到式（3）。

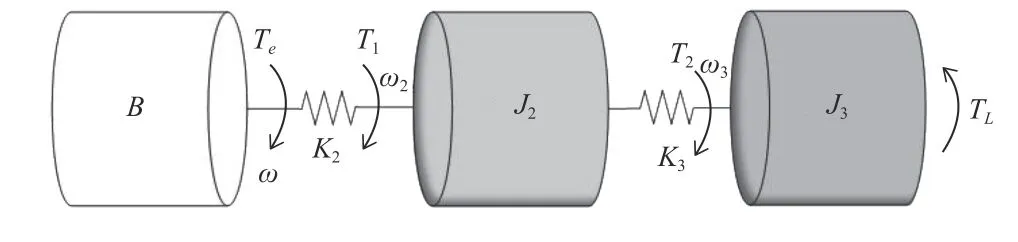
图3 集中质量法的机电耦合模型

式中：J、J2和J3分别为永磁同步电机、减速器和负载的转动惯量；K2、K3分别为减速器和传动轴的刚度；ω、ω2和ω3分别为永磁同步电机、减速器和负载的转速；θ 、θ2和θ3为 角位移；T1、T2和TL分别为减速器输出力矩、输出轴扭矩和负载转矩。

由于系统输入与输出之间存在着力学、电磁以及调速控制系统PID参数的耦合，故将矢量控制模型、机械传动模型和负载模型统一由PMSM模型表示来搭建机电耦合仿真模型。搭建的机械部分和整个伺服传动系统的仿真模型分别如图4和图5所示。

图4 机械部分仿真模型

图5 机电耦合系统仿真模型

1.2 运行品质模型

减速器静动态特性指标主要指减速器刚度、转动惯量、回差以及传递误差、传递效率。而定位误差、跟随误差、稳定性、跟随性和电机振动则为伺服系统的静动态性能指标，这些指标反映了伺服系统的定位能力、定位响应能力、抗负载波动能力以及速度响应能力。工业机器人运行品质主要表现为位姿特性、轨迹特性、静态柔顺性和最小稳定时间[14]。轨迹特性是一种动态特性，表明机器人的动态跟踪性能，伺服传动系统运行品质模型则主要研究工业机器人关节稳态时的轨迹跟踪能力和瞬态响应[15]。

建立如图6所示的伺服传动系统机电耦合运行品质模型。分析机器人关节伺服电机系统转矩、转速变化时间响应以及减速器空程、回差和传动误差等对机器人关节稳定性能的影响。通过机器人运动学和动力学分析核心零部件对机器人整机关键性能指标的影响，包括位姿准确度、轨迹重复度、轨迹速度准确性和轨迹速度波动，核心零部件性能参数与整机性能参数间映射关系如图7。

图6 伺服传动系统运行品质模型

图7 运行品质参数与整机性能参数关系

2 减速器性能退化模型研究

2.1 减速器寿命影响机理研究

减速器本身是一种高精度、高扭矩的传动装置，其内部零件如齿轮、轴承和曲柄轴都具有极强的疲劳强度和刚度，在运转过程中很难出现破坏形式的失效，而导致其失效的原因往往是内部轴承、齿轮等金属零件表面的疲劳、磨损[16]。

以常用于工业机器人传动系统中的RV减速器为对象研究其寿命，其内部轴承均为滚动轴承，不存在金属表面直接接触和相对滑动的情况。但在正常工作时，RV减速器两个摆线齿轮交替旋转，与滚针间存在相对运动，同时滚针在槽内自转，不仅受到旋转带来的磨损，同时也要承受由于相对运动带来的持续不断的剪切力。在工作一段时间后，可能会出现滚针断裂的情况[17]，RV减速器失效如图8所示。

图8 RV减速器失效图

伪失效寿命并不是产品真实的使用寿命，而是人为设定了一个寿命年限，当产品的性能退化到此寿命年限时，即认定该产品“失效”。通过借助伪失效寿命的概念，产品实际寿命较长和不方便进行加速试验的问题迎刃而解。

2.2 减速器性能退化模型

减速器性能退化过程实质上是其传动效率降低的整个过程，可以用传动效率表征性能退化。目前已有的产品退化模型是基于5种基础退化曲线变化而来。5种基础的退化曲线如下

为更合理地描述RV减速器性能退化的完整过程，提出基于不同参数特性两两融合的基础退化曲线，形成10种融合后的退化曲线模型。

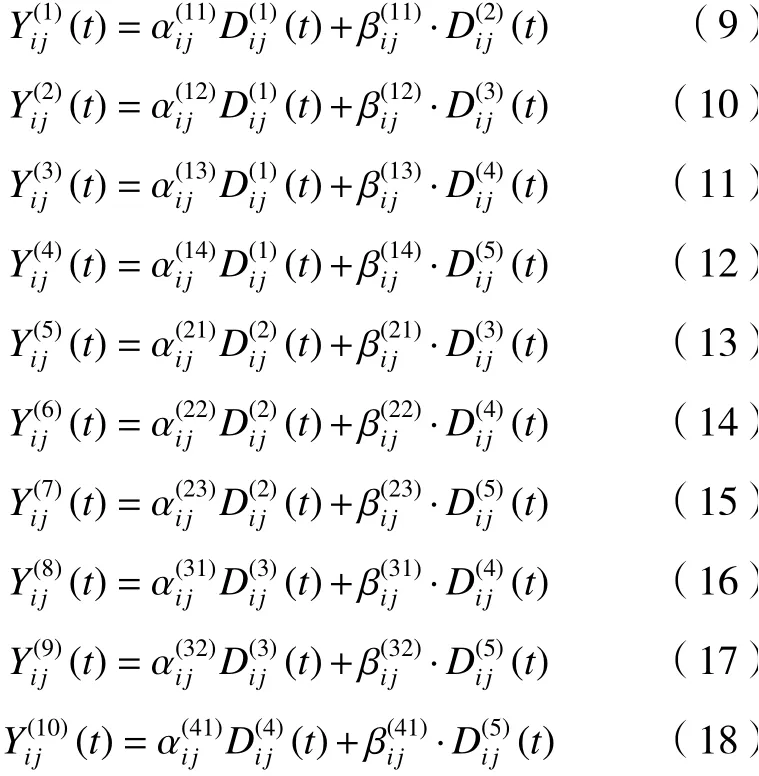
2.3 减速器性能及寿命测试方法

2.3.1 加速退化试验

加速退化试验是通过对减速器设定一个失效阈值，当产品性能退化到设定阈值时，便认定产品“失效”并停止试验。最终通过这段时间内产品性能退化数据对产品在正常工况下的寿命进行预测[18]。在加速退化试验过程中合理控制加速应力的范围，使减速器的失效机理在试验过程中保持不变。但实际上加速应力越大，产品性能退化越快，应用逆幂律模型表达整机性能与加速应力关系[19-20]。

试验选择国内国外RV减速器各两台，测试用RV减速器参数如表1。加速退化工况根据GJB 899A-2009《可靠性鉴定和验收试验》进行定时截尾，具体加速退化试验参数设定如表2，每一阶段的性能退化试验后，对试验减速器系统进行维护，并分别在0 h、50 h、100 h、200 h、300 h、500 h、700 h和1 000 h时刻记录减速器的传动精度、效率、回差和空程。

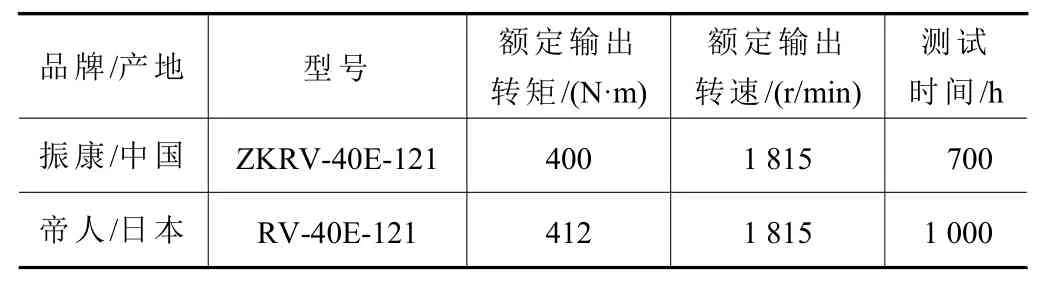
表1 试验测试的RV减速器参数

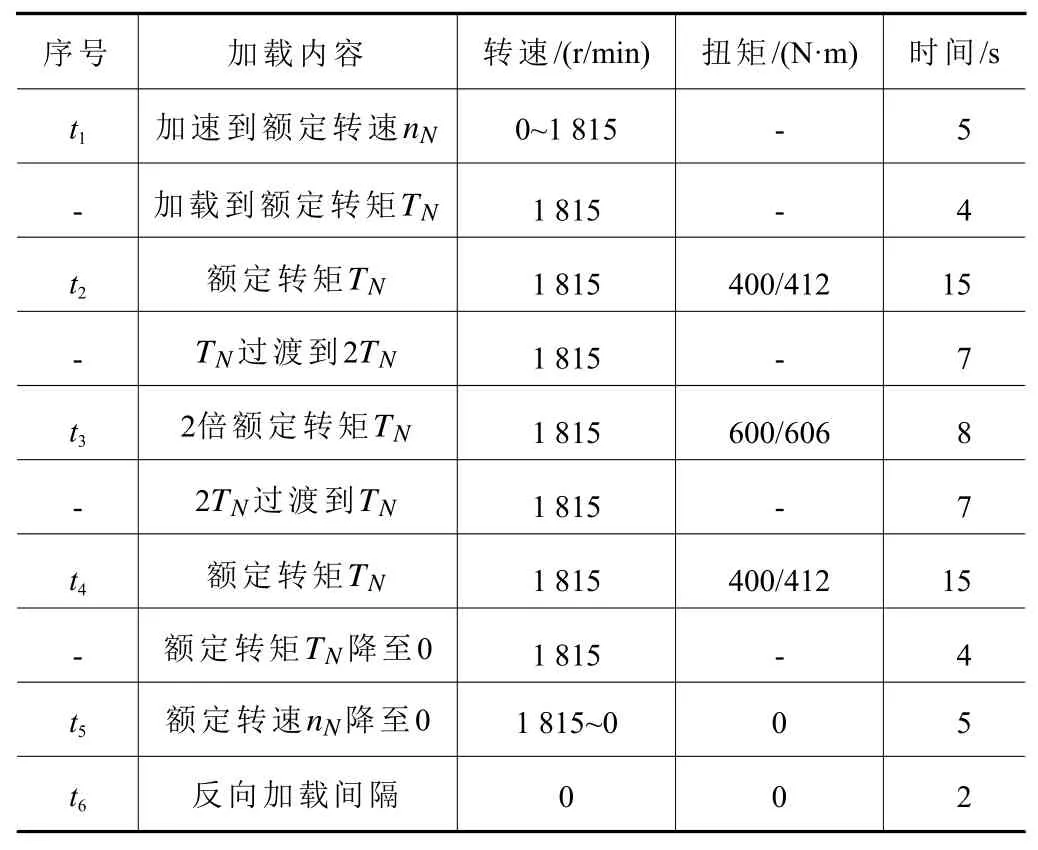
表2 RV减速器加速退化试验单次循环参数表

2.3.2 退化模型准确度评价与试验验证

验证退化模型准确度，需将试验数据与退化模型进行曲线拟合，如图9所示。试验数据中的数据点表示为(xi,yi)，并根据试验数据得到退化模型表示为y=f(x)，拟合后准确度Pi定义为

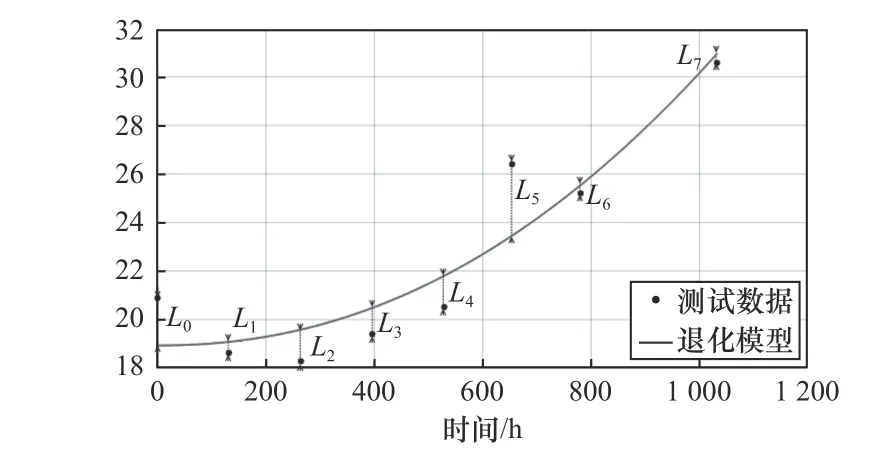
图9 退化模型准确度验证

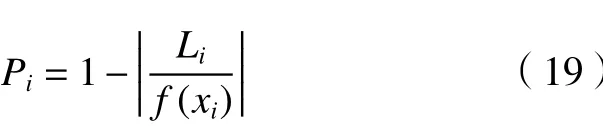
式中：Li=|f(xi)-yi|为测试点与退化曲线的差值。

利用式（19）评价模型中各点准确性的平均值来衡量整个模型的准确性为

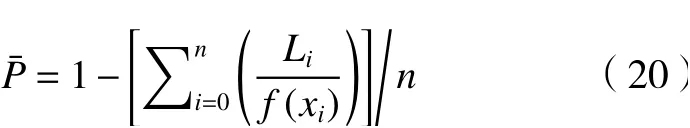
RV减速器性能退化模型准确度如表3所示，试验结果表明：帝人RV40E的整体性能模型平均准确度达到88.57%，单项性能模型平均准确度最高达到99.37%，性能准确度的中位数为85.45%；振康RV40E的整体性能模型平均准确度达到90.21%，单项性能模型的平均准确度最高达到98.17%，性能模型准确度的中位数为90.95%。

表3 RV减速器退化模型准确度

3 伺服系统性能退化模型研究

3.1 伺服电机系统寿命影响机理研究

将伺服电机系统按功能分为控制电路、功率器件、传感器等机械部件，并建立伺服电机系统可靠性串联模型如图10。电机的失效90%以上来自于轴承失效和定子绕组绝缘失效。因此主要对交流伺服电机的轴承和定子绕组绝缘的可靠性及寿命进行分析。

图10 伺服电机系统可靠性框图

建立永磁同步电机轴承和绕组的寿命模型。基于其数学模型，分析加速应力对定子绕组、轴承寿命的影响，确定各部件的加速度寿命系数。

（1）轴承寿命

伺服电机中常用滚珠轴承寿命计算如下：

式中：LR为可靠度R时的轴承寿命，单位为 h；n为轴承的转速，单位为r/min；C为滚珠轴承额定动载荷，单位为N；P为滚珠轴承承受的当量动载荷，单位为N；ε为寿命指数，球轴承为3。fp为载荷因素；fR为可靠度的寿命修正系数；fL为润滑的寿命修正系数；fR、fS为润滑油过滤精度、含水的寿命修正系数；fY为材料熔炼寿命修正系数；fH为表面硬度的寿命修正系数；fT为温度的寿命修正系数；fE为轴向偏斜的寿命修正系数。温度对轴承寿命修正系数可用式（22）计算。

（2）定子绕组绝缘寿命

绝缘材料电阻率随温度的升高而呈指数下降，但温度对绝缘寿命影响很难用数学方法从绝缘材料失效机理进行推导，一般通过大量试验获得相关数据，用统计方法得出其失效规律和经验公式为[21]

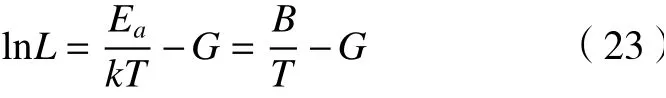
式中：L为平均绝缘寿命，单位为h；T为绝缘材料温度，单位为K；k为玻尔兹曼常数8.617×10-5，单位为 eV/K；Ea、G为与绝缘材料有关的系数。

（3）加速寿命

设电机工作时环境温度为TH1，当量动负荷为P1，轴承温度为TB1，绕组温升为TI1。加速寿命试验时环境温度为TH2，当量动负荷P2，轴承温度为TB2，绕组温升为TI2，则此加速寿命试验条件对电机不同部分的加速系数如式（24）～（26）。

对轴承的加速寿命系数AB

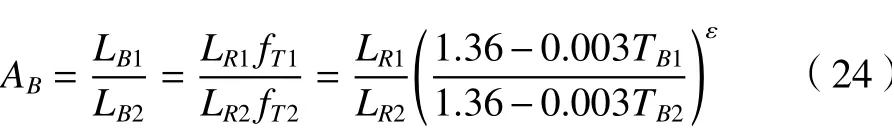
式中：LB1、LB2分别为额定工作、加速寿命试验下的轴承寿命；fT1、fT2分别为额定工作、加速寿命试验下的轴承寿命温度修正系数；ε为寿命指数，球轴承为3。

对绕组绝缘的加速寿命系数AI

式中：LI1、LI2分别为额定工作、加速寿命试验下的绕组绝缘寿命。

对伺服驱动装置加速寿命系数A

试验结果乘以相应的加速寿命系数得到正常试验条件下电机的寿命试验数据。则伺服驱动装置的等效寿命可表示为

式中：Ai和Ti为第i种工况的加速寿命系数和加速试验时间。

3.2 伺服驱动系统性能退化模型

伺服驱动系统性能退化模型是具有时变参数的多项式和Wiener过程，基于加速试验方法的性能退化模型原理如图11。

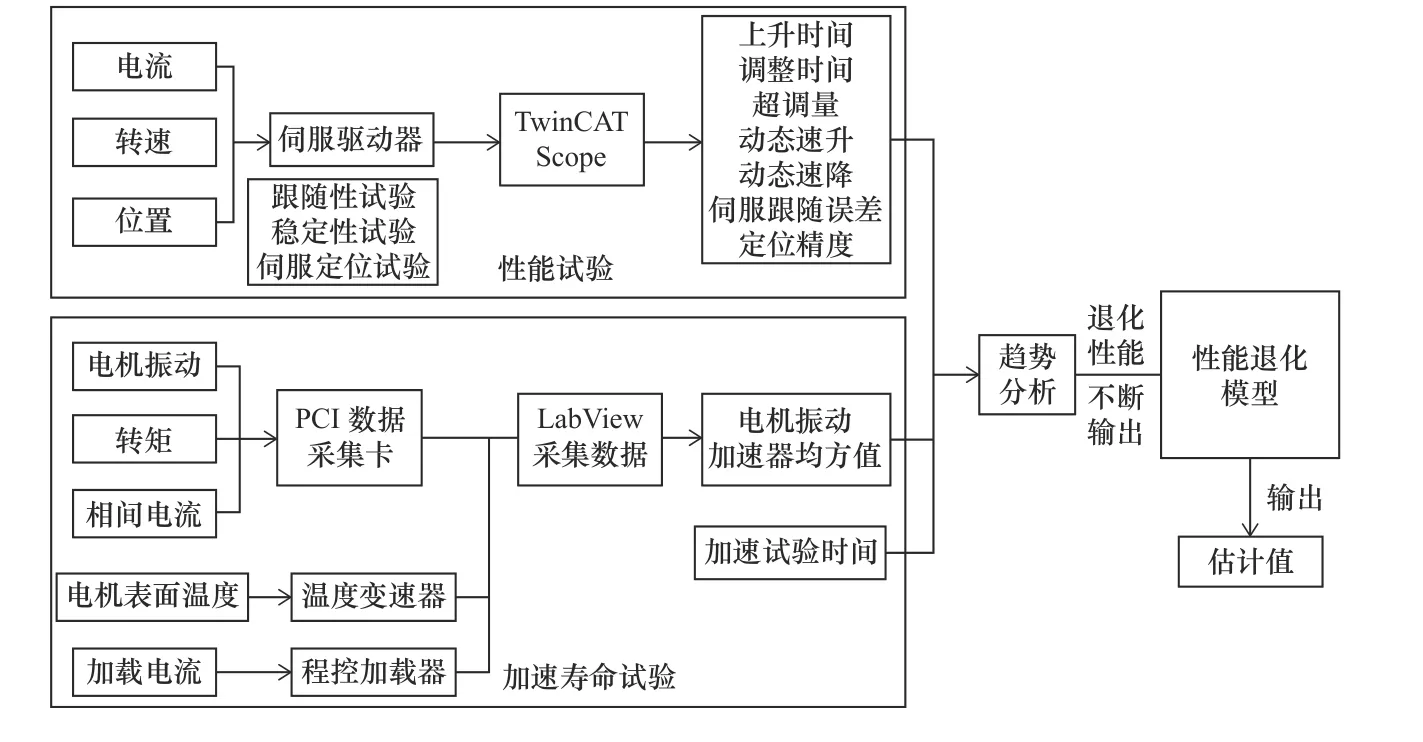
图11 基于加速试验方法的性能退化模型原理

通过对伺服电机进行加速寿命试验，利用加速度传感器采集电机振动、转速、扭矩、电压、电流以及温度等状态参数。在加速试验后，根据电流、转速参数对伺服驱动器进行性能检测，包括跟随性、稳定性和伺服轴定位试验。分析伺服驱动装置的上升时间、调整时间、超调量、动态速升、动态速降、伺服跟随误差和定位精度。通过趋势分析判断性能指标是否有明显的退化趋势，并将退化特征不断通过试验数据输入性能退化模型中，预测伺服系统的性能变化。

振动会使机器人的零部件产生附加磨损从而降低末端定位精度和增加定位时间。此外，振动会对整机频谱特性产生影响，从而导致机器人运行轨迹出现不同程度的偏离[22]。研究振动对机器人整机性能的影响，首先提取干扰噪声信号进行频谱分析，并用傅里叶变换将振动信号进行转换[23]。信号分解常用变换公式为

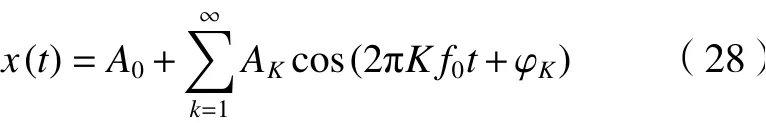
式 中：A0为 信 号的直流分量；AKcos(2πK f0t+φK)为信号的各阶谐波分量；AK为信号谐波分量的振幅；φK为 信号谐波分量的相位角；f0为振动基频。

此处选用电机振动加速度作为模型参数，形成如下两种伺服电机退性能化模型。

（1）三次多项式退化模型

用多项式表示性能随时间的变化

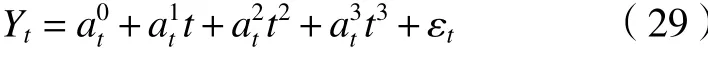
式中：Yt为伺服电机振动加速度；t为电机运行时间；个时变多项式系数；εt为误差项。

（2）Wiener过程退化模型[24]

Wiener过程的电机振动退化模型可以表示为

式中：Xt为 伺服电机振动加速度；a为初始状态；µ为漂移参数；σ为扩散参数；W(t)为标准的Wiener过程，并且用 σW(t)～N(0,σ2t)来表示退化过程随时间变化的概率分布。

3.3 伺服系统性能及寿命测试方法

伺服系统性能及寿命测试方法主要分为电机加速寿命试验和驱动器性能试验。寿命试验可以了解伺服电机的寿命特征、失效规律，确保产品失效率和平均寿命等可靠性指标。性能试验主要研究伺服驱动装置的性能随时间的变化，试验项目如表4所示。

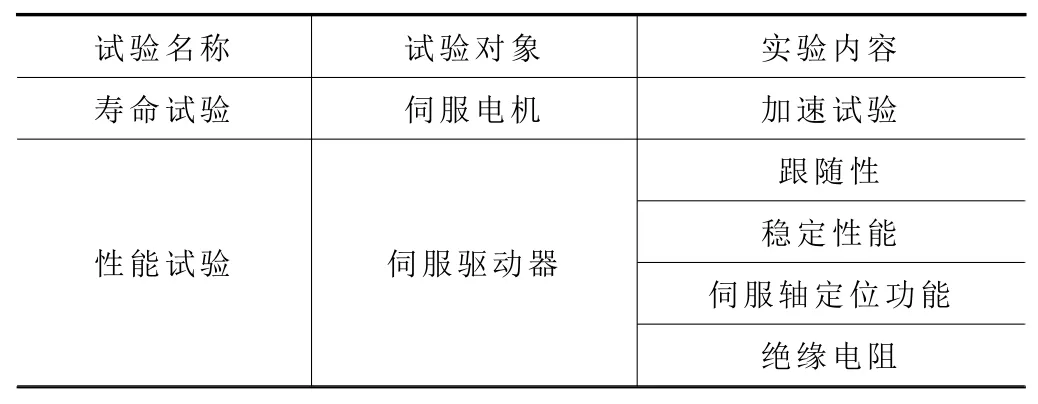
表4 伺服系统性能及寿命测试试验项目

3.3.1 加速退化试验及性能测试

试验选用多摩川、华大、迈信和松下，其产品对应的伺服电机及伺服驱动器参数如表5。伺服电机系统加速寿命试验以20 s一个循环周期，加载一个周期后改变电机旋转方向，以100 h为一个周期对试验伺服驱动系统维护，并进行性能试验，监控主要性能参数变化，加速试验循环参数如表6。

表5 试验样品参数及加速试验时间

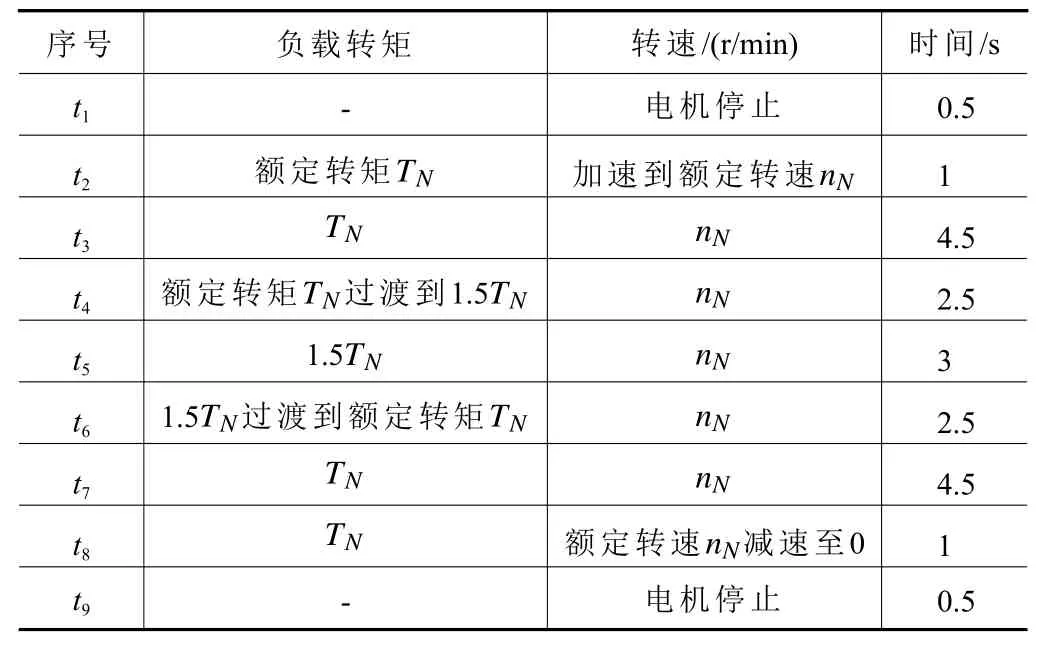
表6 伺服电机系统加速试验循环参数表

3.3.2 退化模型准确度评价与试验验证

对伺服系统的跟随性、稳定性、伺服轴定位性能参数进行Daniel趋势检测法分析，其误差均方根低于理论值（P＜0.01）验证试验过程中各性能指标参数无显著变化，分析结果如图12。进行多次Wiener迭代优化，最终得到伺服系统退化模型的100 h预测准确度，其中松下准确度最高91.90%，多摩川准确度最低85.07%，华大准确度为87.73%，迈信准确度为89.56%，平均准确度为88.41%。相比较Daniel趋势检测，Wiener退化模型精度最高且预测精度稳定性相对较好，可确立最终退化模型为Wiener过程的性能退化模型，并以此来描述退化过程随时间变化的不确定性。

图12 基于Daniel趋势检测的参数误差

4 结语

（1）分析工业机器人核心部件静动态特性，建立工业机器人伺服电机、精密减速器等在内的核心部件性能退化模型和、性能退化评估方法及测试技术。同时优化性能退化模型，对伺服系统退化模型参数用Daniel趋势检测法进行估计分析，并最终确立以Wiener过程的性能退化模型。通过试验验证，机器人伺服系统和精密减速器性能退化模型的准确度均大于85%。鉴于时间和成本等因素的限制，目前仅针对主流品牌和型号的产品开展了测试试验和模型迭代优化，因此模型的普适性不强。随着后期不断开展技术成果的应用与推广，样本量逐渐增大，模型将不断优化迭代并逐步归一，增强模型的通用性和普适性，进一步提高预测的准确度。

（2）建立了运行品质参数与整机性能评价参数之间的映射关系。设置加速寿命退化试验确立减速器、伺服系统的性能退化模型中静动态特性参数变化趋势，并通过试验评估方法得到减速器、伺服系统影响机器人整机性能的主要参数的准确度。减速器主要通过刚度、转动惯量、回差以及传递误差和传递效率5个参数影响机器人的整机性能，伺服系统主要通过速度阶跃下响应上升时间、调整时间及超调量，抵抗转矩负载扰动的动态速降、速升，跟随误差，定位精度7项参数来影响机器人整机性能。