不同支链排布的3-PRS并联机构姿态能力比较

陈国旺 范秋垒 罗 超

（①重庆智能机器人研究院，重庆 400714；②重庆大学，重庆 400030；③四川轻化工大学，四川自贡 643002）

文献[1]首次提出零扭矩3-[PP]S类并联机构，具有3个独立自由度（2个转动，1个平动：2R1T）。直至当前，以2R1T运动的3-[PP]S类并联机构作为装备制造结构本体的工业应用已经十分广泛，如：Z3摆 角 头[2]、A3摆 角 头[3]、Tricept混 联 机 床[4]和Exechon混联机床[5]等。Z3摆角头的本体结构为3-PRS并联机构而A3摆角头的本体结构改为3-RPS并联机构，Tricept的机构模块为3UPS-UP并联机构，Exechon的并联模块为2UPR-SPR并联机构。

由于2R1T机构本身运动特性，2R1T并联机构成功应用在机床领域。因其巨大商业价值，目前仍然有颇多国内外学者研究2R1T变体机构，旨在找出性能更优，结构更合理紧凑的2R1T机构[6]。并联机构具有良好性能是能实际工程应用的理论支撑和前提，因此，找出一个合理评价机构性能的评价指标显得尤其重要。刘辛军等[7-8]提出用于并联机构优化设计的运动/力传递性能指标。Wang FB等[9]得到2-UPR-SPR并联机构局部传递性能指标和全域性能指标，将其作为机构运动/力传递性能评价准则，获得2-UPR-SPR 并联机构的相关指标性能图谱和优化结果。Assal S等[10]基于无量纲设计参数空间，以工作空间指数（WI），运动/力传递指数，运动和动态灵活指数以及刚度指数作为综合性能评估。Pond G等[11]运用条件数和奇异值，对3种不同布局的3-PRS机构进行了优化比较，选出了最适于工业应用的布局。Sun T等[12]运用3-PRS机构雅可比矩阵的条件数作为全局性能指标，综合考虑伴随运动及实际工程运动约束，采用非线性规划方法对3-PRS机构进行了优化设计。Gao Z等[13]运用并联机构的系统刚度和灵巧度来优化机构的结构尺寸。Liu X J等[14]运用条件数及刚度来优化并选择三自由度球面并联机构的连杆长度并分析机构操作性能。

确定并联机构的评价指标后，可以建立并联机构尺度优化模型。尺度优化模型包括机构结构参数，材料选择（决策变量）、机构避免奇异位置的几何条件及实际工况下的几何条件（约束条件）及单个或多个性能指标取得极值（目标函数）。目前，学者对尺度优化模型的研究主要集中在含约束条件的优化目标函数。Belkacem B[15]建立基于运动-弹性静力学性能的多目标优化模型，然后使用进化遗传算法来找出相互冲突的多个目标函数之间的所有可能权重。He K等[16]选择工作空间体积、灵巧度、静态效率和刚度作为多目标优化的目标函数，优化机构的结构参数。Huang GY等[17]建立基于末端执行器的刚度模型和灵活性的多目标优化模型，利用遗传算法进行多目标优化，得到Pareto前沿图。侯雨雷等[18]以机构姿态工作空间的点数为优化目标，分别建立3-PCSS/S、3-PSS/S球面并联肩关节仿生机构的约束优化模型，再采用遗传算法（GA）优化机构尺寸参数，得到较好优化结果。Wang L P等[19]提出统一逆运动学、雅可比矩阵和运动/力传递指标模型。在此基础上，对关键结构参数进行优化设计。

以两种3-PRS并联机构为研究对象（文中称为机构A、B），第一章对机构A、B结构进行了简要描述。第二章，分别建立了两者的位置反解模型。第三章，基于文献[7]提出的运动/力传递指标，提出以满足许用运动/力传递指标的封闭曲线的最大内切圆半径κGTOC为优化目标函数，满足机构全局运动/力传递指标GTI为约束条件，建立一个有约束单目标约束优化模型。第四章运用DE优化算法求解上述第三章优化模型，得到结构最优结构参数，并用实例分别比较机构A、B优化前后的运动/力传递性能。第五章对该论文进行了精简总结。

1 3-PRS并联机构结构描述

以下机构均为两转动一移动（2R1T）3自由度3-PRS并联机构。图1为Z3并联机构[20]，称为机构A。图2为通过改变支链排布得到的Z3变异结构，称为机构B。

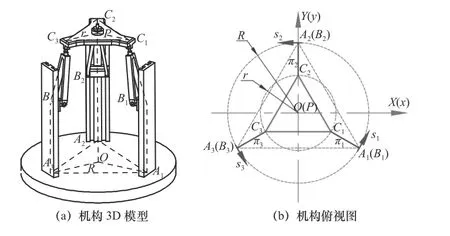
图1 3-PRS并联机构A(Z3)

图2 3-PRS并联机构B

如图1a为A机构三维运动简图。该机构由动平台C1C2C3，定平台A1A2A3以及3条结构相同的PRS支链组成，动、定平台均为正三角形。自定平台起，P副轴线过定平台理论顶点Ai且垂直定平台平面，R副轴线垂直P副轴线，S副与动平台理论顶点Ci重合(i=1,2,3)。支链其单位矢量为u i，R、r分别为定、动平台外接圆的半径，为移动驱动副(i=1,2,3)。在定平台上建立定坐标系(或称为参考坐系){f}:OXYZ，X轴正向平行矢量A1A3，Y轴正向与矢量A1A3垂直，按右手法则确定Z轴。在动平台上建立运动坐标系{m}:Pxyz，其轴线方向和定坐标系轴线方向一致。机构A展开图中，点Ai与Bi(i=1,2,3)重合及动、定平台角平分线重合，各支链输入旋量si(i=1,2,3)，3条支链BiCi(i=1,2,3)分别被限制在过定平台对角线的3个平面πi内运动(i=1,2,3)，如图1b所示。

用上述方法，描述图2机构B。机构B组成结构和机构A相同。如图2a为机构B三维运动简图。对机构B：定坐标系(参考坐标系){f}和运动坐标系{m}与机构A相同。机构B展开图中，点Ai与Bi(i=1,2,3)重合，动、定平台角平分线夹角为α(第二节已求解α)，3条支链BiCi(i=1,2,3)分别被限制在平面πi(i=1,2,3)内运动，3平面与动平台理论边线重合，如图2b所示。

2 3-PRS并联机构位置反解模型

用Z-Y-Z型Euler角(φ,θ,ψ)表示3-PRS并联机构动平台的运动姿态。表示其姿态的旋转矩阵为

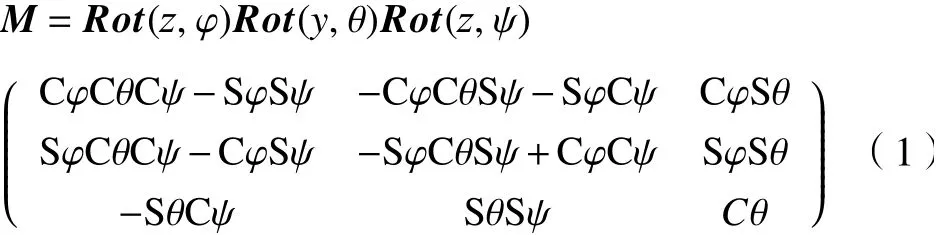
式中：Rot(y,θ)表示绕y轴转θ角的旋转矩阵，其余类似；Sθ、Cθ是正弦函数sinθ和余弦函数cosθ的缩写，其余类似。

据图1可知，可得并联机构A位置反解方程。由文献[20]结论可得，并联机构A没有绕动平台法线的扭转，此时满足ψ=-φ。故，机构A姿态矩阵可表示为

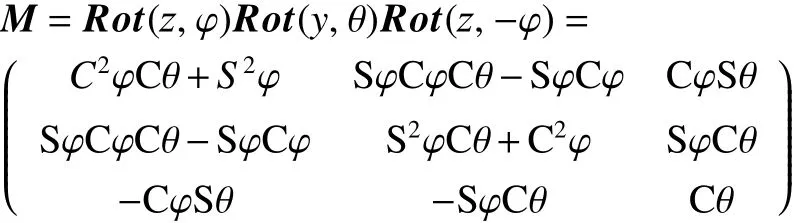
设动平台参考点P为P=(XP,YP,ZP)T，点Ai在定系{f}:OXYZ中的坐标矢量为

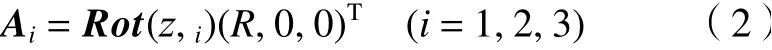
式中：ξi=(4i-5)π/6(i=1,2,3)，其余类似。

点Ci在动系{m}:Pxyz中的坐标矢量分别为

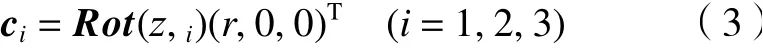
则C点在定系{f}:OXYZ中的坐标矢量为

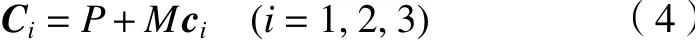
那么，移动驱动杆长qi可表示为

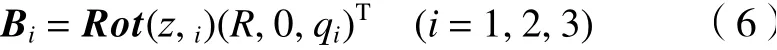
由于支链BiCi(i=1,2,3)被限定在特定的平面内运动，故有平面约束方程组

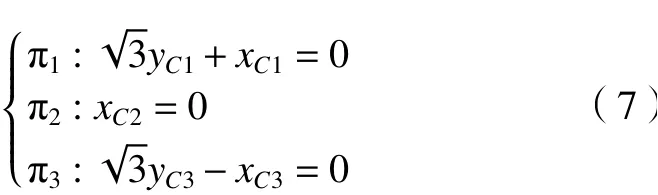
已知动平台位姿ZP和(θ,φ)时，可由式（7）求出动平台参考点P的XP和YP表达式，即XP、YP为机构伴随运动。

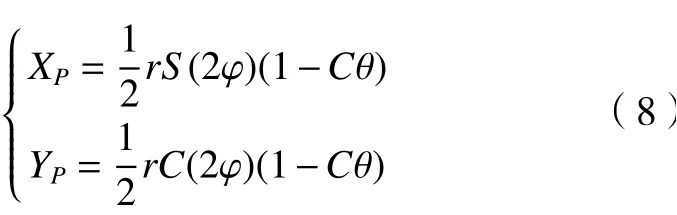
Z3并联机构的位置反解方程可用式（5）求得。

同理，据图2可知，可得机构B位置反解方程。机构B有绕动平台法线的扭转，此时ψ+φ≠0。故，机构B姿态矩阵用式（1）表示。

设动平台参考点P为P=(XP,YP,ZP)T，点Ci在动系{m}中坐标矢量为式（3），点Ai在定系{f}中的坐标矢量为

C点在定系{f}中的坐标矢量为式（4），移动驱动杆长qi可表示为式（5），Bi点坐标表示为式（6）。

机构B中平面约束方程组为

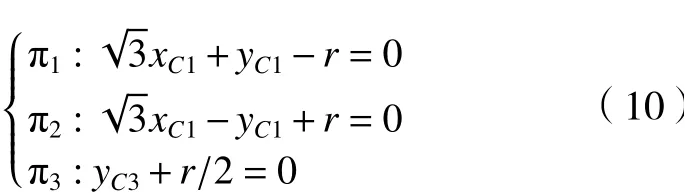
由于机构B伴随运动表达式较复杂，这里设式（1）姿态矩阵为

同理，由式（1）、（10）、（11）可求得机构伴随运动XP、YP、ψ如下。

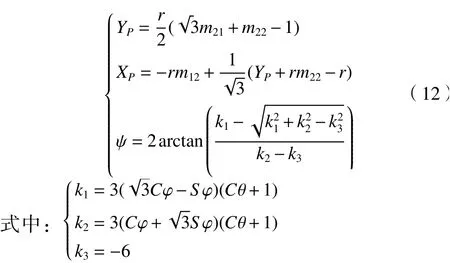
并联机构B的位置反解方程也可用式（5）求得。

3 机构性能分析

3.1 机构运动/力传递指标

据文献[20-21]的研究结论可知，机构A,B动平台均受3个约束纯力。纯力分别过球副中心Ci且垂直于动平台对角线PCi(i=1,2,3)。故，机构A、B的约束力旋量(constraint wrench screw,CWS)可分别表示为

式中：i=1,2,3。

由于各支链的P副为驱动副，输入运动为沿Z轴纯移动，故机构A、B的输入运动旋量(input twist screw,ITS)均为

各支链的传递力旋量(transmission wrench screw,TWS)均为纯力，过点Bi且沿BiCi方向。故机构的TWS为

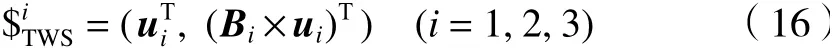
设 机 构 的 输 出 运 动 旋量(output twist screw,OTS)为

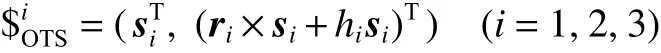
式中：s i为第i支链OTS的轴线单位矢量(主部)；r i为第i支链OTS轴线上一点的坐标矢量；hi为第i支链OTS的节距。

根据互易旋量关系，可得[22]

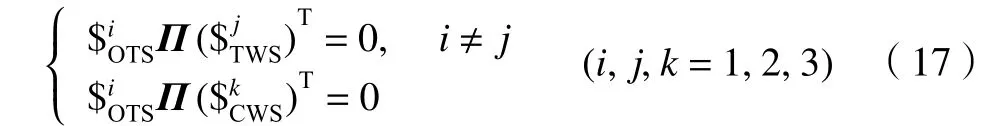
式中：Π为对偶算子，为3阶单位矩阵；03为3阶0方阵。

据文献[24-25]的定义，第i支链的输入传递指标(input transmission index,ITI)为

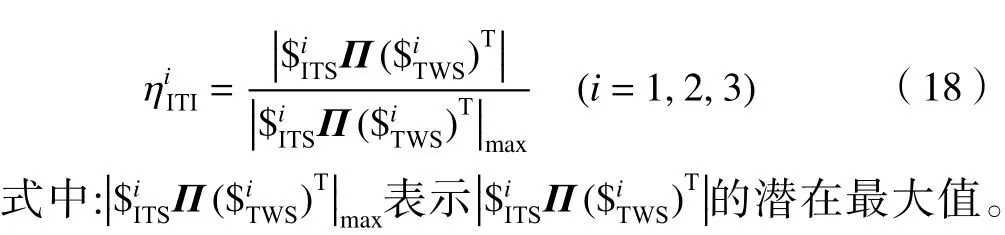
第i支链的输出传递指标(output transmission index,OTI)为

于是，机构A、B的LTI可表示为

3.2 机构优质传递姿态工作空间

若已知机构尺寸参数l,r，当给定定平台结构参数R及动平台参考点P的坐标ZP时，机构ηLTI为姿态角φ、θ的函数，即

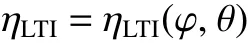
将所有满足ηLTI(φ,θ)≥[ηLTI]的姿态(φ,θ)集合，定义为机构的ZP截面优质传递姿态工作空间(good transmission orientational workspace,GTOW)。其中，[ηLTI]为许用传递指标，本文取[ηLTI]=0.7。以点θ=0为圆心，作出GTOW的最大内切圆(maximum inscribed circle,MIC)(图3蓝 色 粗 虚 线 绘 制 的 圆 为MIC即κGTOC)，称为机构的GTOC。以下用GTOW的最大内切圆半径度量GTOC，并记作

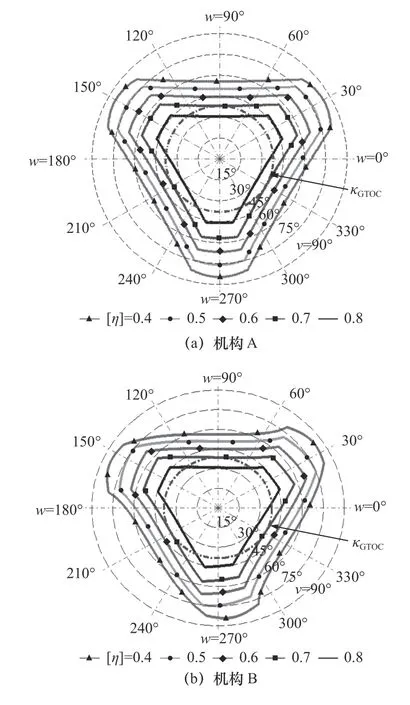
图3 优化前机构LTI等高线(ZP=100 mm)

对于给定的ZP，将GTOW的最大内切圆内的所有姿态集合记为

对ΩGTOC内的所有姿态(φ,θ)，求ηLTI(φ,θ)的均值，称为机构的ZP截面GTI，其表达式为

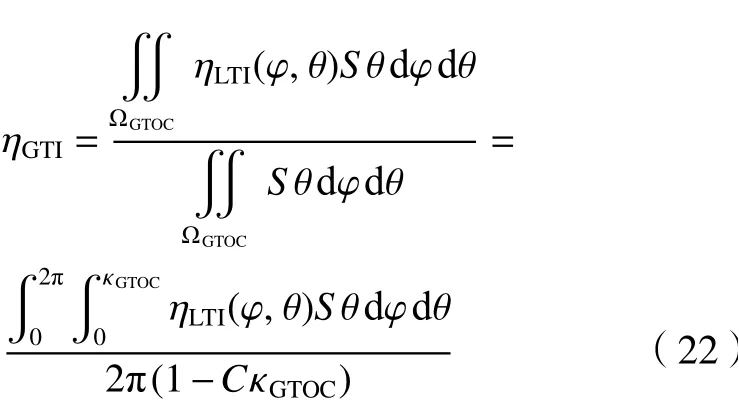
3.3 机构性能比较分析实例

机构A、B均取经验尺寸参数，R=100 mm，r=70 mm，L=400 mm。采用第3节的性能方法分析机构A、B的运动/力传递特性。

如图3所示，为两机构的局部传递性能指标分布曲线。由于沿ZP方向的移动，对3-PRS并联机构的姿态无影响，因此，可取一固定截面，研究机构整体的姿态能力，本文取ZP=100 mm。机构A(Z3主轴头)的ZP=100 mm截平面内的LTI等高线如图3a所示，[η]=0.4时，最外围红色边界曲线附近区域对应机构姿态能力较差，及机构较易形成或接近奇异位姿，即机构运动/力传递性能不良好。[η]=0.7围成的蓝色实线区域为机构优质传递工作空间(GTOW)，其运动远离奇异位置，这也是理想轨迹规划空间。在GTOW内，机构运动/力传递效率较高，传递性能优良。在不同倾摆角ω下，Z3机构的性能分布曲线沿竖直方向呈轴对称图形。在方位角ω=30°、150°、270°区域，倾摆角范围较大，其余区域倾摆能力一般。因κGTOC表示任意方位角下均可达的最大姿态能力，由GTOW边界上的最小倾摆角确定。经计算得优化前Z3机构的κGTOC=38.02°。

同理，在不同倾摆角ω下，机构B的性能分布曲线也成单轴对称图形，如图3b所示。在方位角ω=30°、150°、270°区域，倾摆角范围均较大，而其余方位角下的摆动性能较差。机构κGTOC=38.48°。

经比较，机构A相对机构B，其κGTOC增加0.46°，说明变异后的Z3机构同样有良好的姿态能力。同时，可应用机构κGTOC，定量筛选不同支链排布的同类并联机构。

4 机构姿态能力优化

4.1 机构姿态能力优化模型与算法

由于按一定比例缩放机构尺度，机构性能指标不变和Z轴方向的位移不会影响机构的姿态，因此，可预先给定定平台结构参数R和工作空间截面高度ZP，以尺度参数(r,l)为结构设计变量，即决策变量为

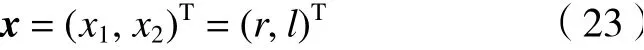
根据实际应用需要，设计者期望机构具有尽可能大的姿态能力，因此，可将目标函数设置为

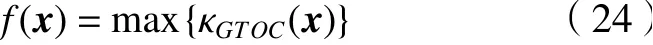
设计者通常期望机构具有良好运动/力传递性能，因此，机构运动过程中GTI应较大。于是，引入以下约束条件。

综上可知，机构A、B的GTOC最大化设计问题均为非线性约束优化模型，其目标函数为式（23），约束函数为式（24）。

应用DE算法求解机构约束优化问题式（23）时，还需处理不等式约束函数式（24）。文中应用DEB[27]提出的可行性规则处理约束函数，为此，引入候选解x的约束违反度函数

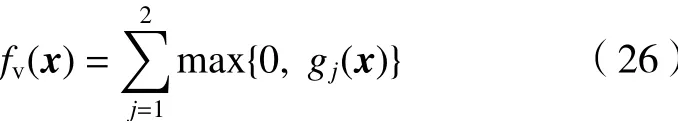
比较两个候选解的DEB规则为：对于任意两个候选解x1和x2，若满足以下条件之一：

（1）fv(x1)=0且fv(x2)＞0。

（2）fv(x1)=fv(x2)=0且N(x1)＞N(x2)。

（3）fv(x2)＞fv(x1)＞0。

则x1优于x2。

应用DE算法求解第4.1节机构尺度优化模型的计算流程图4所示。

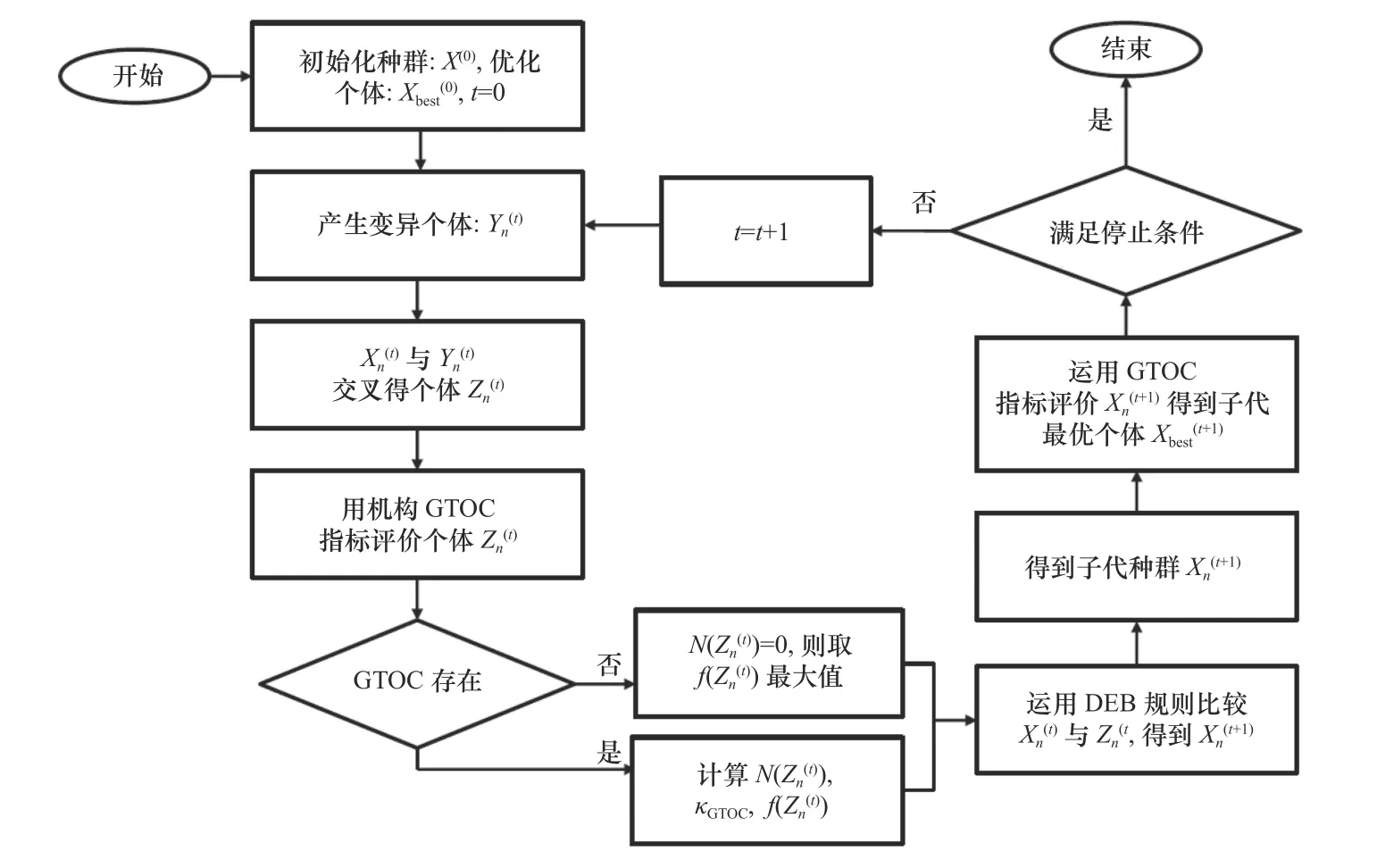
图4 求解机构尺度优化问题的DE算法框图

4.2 机构姿态能力优化实力

给定机构定平台外接圆半径R=100 mm，由于ZP方向的移动与机构姿态角独立，无相互影响，因此，可设机构ZP=100 mm，由DE算法求出4.1节优化模型机构A、B的最优解分别为r=79 mm，L=589 mm；r=76 mm，L=546 mm。运用3.3节方法绘制机构A，B优化后的性能边界曲线，如图5所示。分别对比优化后机构A、B的姿态能力，两者倾摆能力较好区域仍然在方位角ω=30°,150°,270°处，其余方位角的倾摆角依然较小。优化后，机构A、B的κGTOC分别为40.67°,40.52°，略微减小0.15°。但是，分别比较优化前后的机构A或机构B，增长角度比较可观，分别增长2.65°,2.04°，说明优化模型与方法是十分有效的，数据如表1所示。

表1 机构κGTOC比较

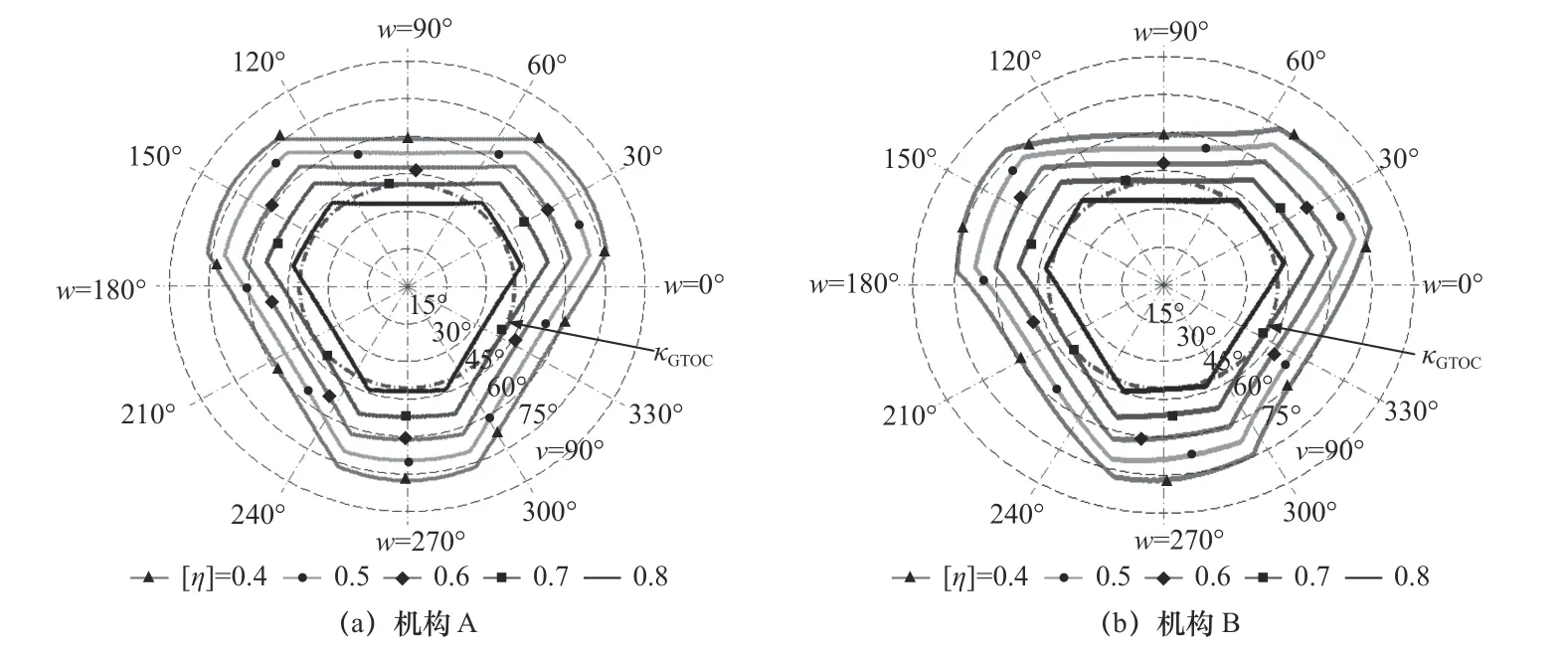
图5 优化后机构LTI等高线(ZP=100 mm)

5 结语

（1）以旋量理论为理论基础，建立机构局部性能指标LTI的解析计算式，并给出全域指标GTI的计算方法。

（2）在给出GTOC模型基础上，建立机构最大内切圆半径κGTOC最大化的尺度参数约束优化设计模型。给出应用DE算法求解该问题的步骤和约束处理方法。

（3）变异前后机构的比较分析表明，相同尺寸的机构之间的κGTOC差异较小，优化前机构B比机构A的GTOC稍大0.63、GTI稍小0.003。通过DE算法优化后，两种机构的GTOC、GTI指标均得到改善，机构A的GTOC、GTI分别提高了7.35、0.012；机构B的GTOC、GTI提高了7.03、0.015。优化后机构B比机构A的GTOC稍大0.31、GTI没有变化。结果表明，求解机构尺度优化DE优化算法是可行有效的。[1]Z latanov D,Bonev I A,Gosselin C M.Constraint singularities of parallel mechanisms[C].2002 IEEE International Conference on Robotics and Automation (ICRA 2002),2002,1:496-502.