借“搬移”巧添线构全等变“通途”

文／黄萍

从全等三角形开始，几何越发充满智慧，有时一条辅助线能使“天堑”变“通途”。平移、旋转、翻折等变换只改变图形的位置，不改变形状与大小，变换前后图形全等。若把这几种变换（组合）称为“搬移”，我们可以通过“搬移”巧添辅助线，构造全等三角形，从而解决问题。

例如图1，E是BC的中点，点A在DE上，且∠BAE=∠D，求证：AB=CD。

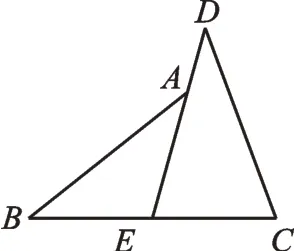
图1

方法1依托已知等边“搬移”三角形

【分析】如图2，延长AE到F，使EF=AE，连接CF，则△ABE≌△FCE，所以CF=BA，∠F=∠1=∠D，所以CD=CF=AB。

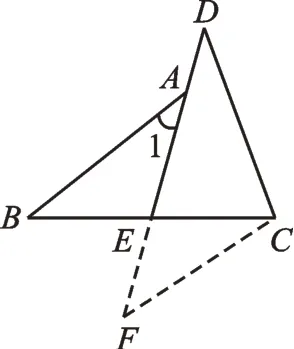
图2

【点评】构造全等三角形是解决本题的关键。本题思路是利用倍长过中点的线段，构造“八字形”全等。

方法2指向待证等边“搬移”三角形

【分析】如图3，在DE上取点F，使CF=BE，因为BE=CE，得CF=CE，则∠CFE=∠CEF，所以∠DFC=∠AEB。再根据∠1=∠D，证得△ABE≌△DCF，则AB=CD。

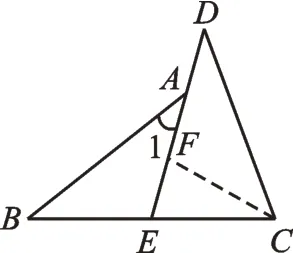
图3

【点评】若待证的结论一定“真”，则由它也能打开思路。运用目标启发思考也要学会哦。

研究图形的基本视角是“边”和“角”，我们前面利用相等的边构造全等三角形，下面再看看相等的角。

方法3由等角出发“搬移”三角形

【分析】基于∠1=∠D这一条件，我们不妨“搬移”△CDE。如图4，使∠D与∠1重合，可这样叙述辅助线：在DE的延长线上取点F，使BF=BE。余下的小读者自己完成哦！（方法2也可以认为是从“角”的角度考虑。）

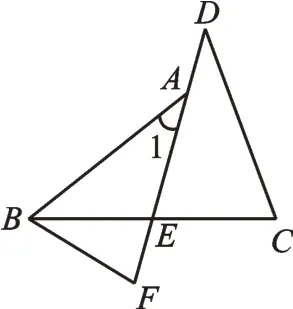
图4

从相等的边和相等的角这两个视角出发，还有其他搬移方法，同学们试试看吧！

初学全等，我们不妨借力“搬移”来投石问路，通过观察，思考如何合理添加辅助线，构造全等三角形。当你和各种图形“相处熟悉”了，解题自然就水到渠成啦！