基于ARIMA 和LSTM 的瓦斯浓度预测研究

李丹青，杨超宇

（安徽理工大学a.管理科学与工程系； b.经济与管理学院，安徽 淮南 232000）

瓦斯灾害是威胁煤矿安全高效生产的主要灾害之一， 对矿井下瓦斯浓度变化趋势精准预测是预防瓦斯事故发生的重要方法［1］。 许多专家学者在瓦斯预测方面做了大量的研究。 李树刚等［2］利用循环神经网络的方法建立了瓦斯浓度预测模型， 有效提升了预测的精确度；张震等［3］基于ARIMA 构建了瓦斯浓度预测模型；孙卓越等［4］建立了长短时记忆神经网络动态预测模型，实时预测瓦斯浓度的未来趋势。上述研究仅选用ARIMA 模型或LSTM 神经网络模型等单一模型进行瓦斯浓度预测， 无法对预测模型的优劣得出评价。 本文选用ARIMA 模型和LSTM 模型以实测的瓦斯浓度数据作为训练样本进行瓦斯浓度的预测， 通过对2 种模型得到的预测结果的对比分析，选出较优的预测模型，为瓦斯浓度预测提供一定的依据。

1 预测模型介绍

1.1 ARIMA 模型

ARIMA 差分自回归移动平均模型是由Box 和Jenkins 提出的一种经典的时间序列预测模型， 简记为ARIMA (p，d，q)，其中：AR 为自回归模型；p 代表自回归阶数， 用于获取自变量；d 代表差分次数；MA为移动平均模型；q 代表移动平均阶数，用于时间数据的平滑处理。 ARIMA 模型不仅可以处理平稳序列，还可通过差分来处理非平稳序列［5］，该模型的数学表达式为

利用ARIMA 模型预测的具体步骤为：（1）数据平稳性检验与处理。 通常平稳性检验的方法分为直接观察法和单位根检验法2 种。 直接观察法通过绘制数据序列图判断其是否平稳， 单位根检验法通过计算T 检验值来判断序列是否平稳。 （2）确定ARIMA 模型的p、q 值。 通过观察样本的自相关图和偏自相关图来选取参数p 和q，一般以自相关图和偏自相关图中各自截尾的位置作为p 和q 的最大值，然后利用贝叶斯信息量准则（BIC）或赤池信息量准则（AIC）从多组p、q 中选择一组最优参数。 （3）模型的残差检验。 通过绘制模型的残差自相关图和残差偏自相关图来判断残差是否服从正态分布。 （4）模型预测。

1.2 LSTM 模型介绍

LSTM 模型通过3 种特殊的门控装置选择性地存储和遗忘信息， 通过控制全局记忆达到延缓记忆衰退的效果［6］，其结构如图1 所示。

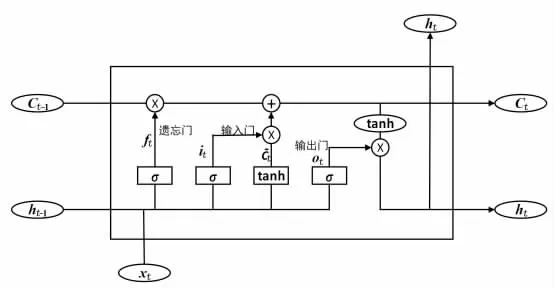
图1 LSTM 结构

2 实证分析

本文实验采取山东省某矿进风巷掘进工作面2021 年1 月21 日5 时 至2021 年1 月22 日5 时 的瓦斯实测数据作为样本数据，分别采用ARIMA 模型与LSTM 模型进行预测，并将预测结果进行对比。

2.1 利用ARIMA 模型进行预测

（1）数据平稳性检验与处理

运用单位根检验法（ADF）判断瓦斯浓度数据序列是否平稳，结果见表1。 由表1 知，原始时间序列为非平稳序列， 经过一阶差分处理后的序列为平稳序列，模型中d 确定为1。

表1 单位根检验结果

（2）确定模型阶数

绘制模型的自相关图（ACF）和偏自相关图（PACF)（图2）。 由图2 知自相关系数和偏自相关系数在滞后阶数为3 之后开始衰减， 当滞后阶数为4时其衰减为0， 因此模型的p、q 可能取值为0、1、2、3。 进一步采用BIC 信息准则来判断p、q 的最优值，BIC 信息准则的结果见表2。 由表2 可知，ARIMA（2，1，2) 对应的BIC 结果为最小值， 因此可以确定p＝2，q＝2 为模型的最优参数。

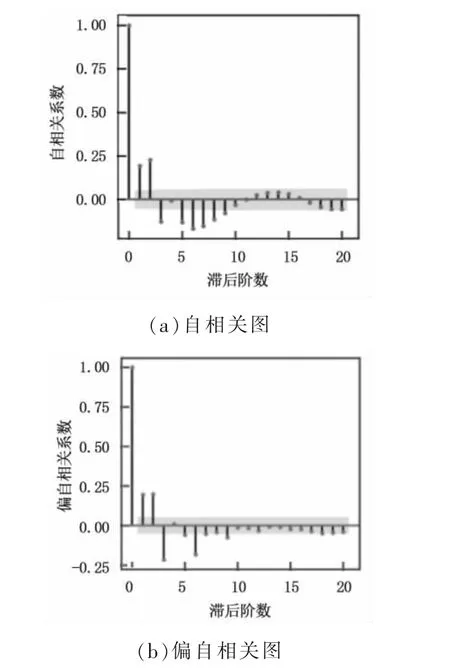
图2 自相关图和偏自相关图

表2 BIC 信息准则分析结果

（3）模型的残差检验

为了判断模型的残差之间是否相互独立， 以及验证模型是否成立， 利用模型残差自相关图像（ACF）和残差偏自相关图像（PACF）（图3）来进行检验。 由图3 知，图中的点基本上处于置信区间内，模型的残差检验通过检验。

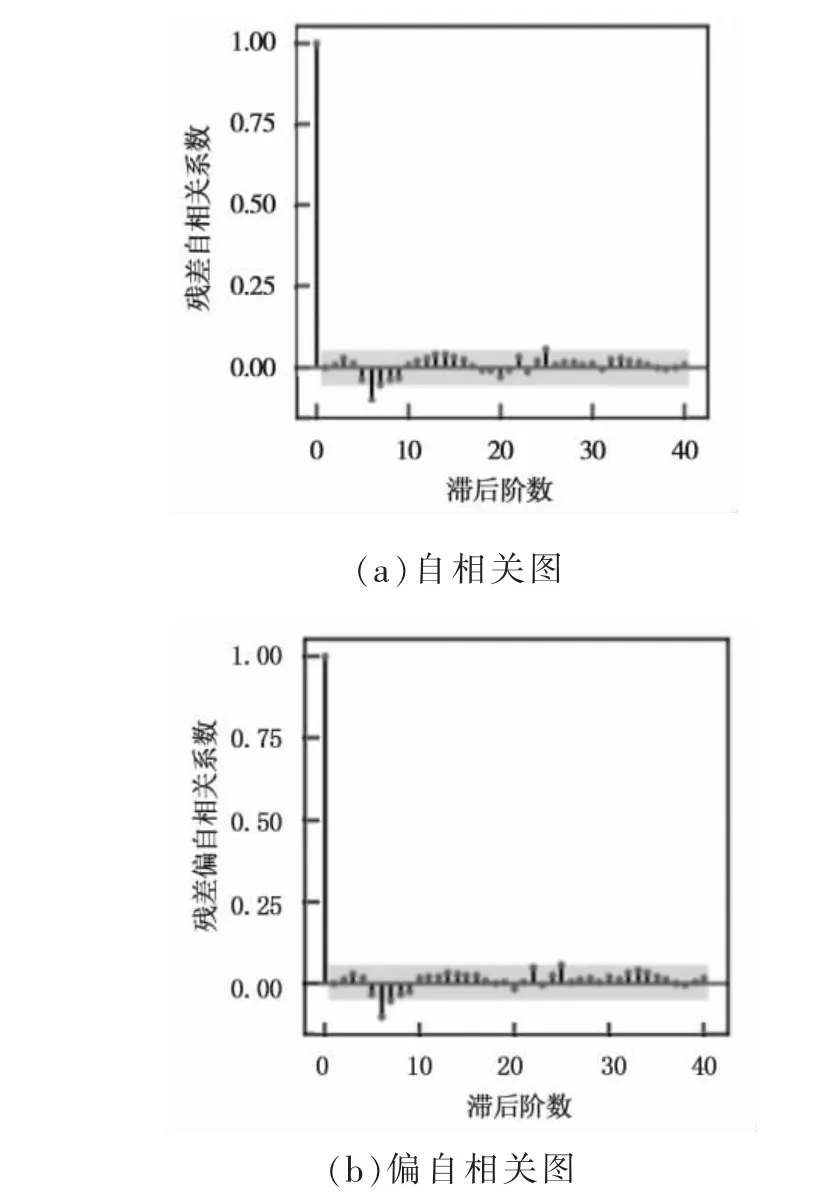
图3 残差自相关图和残差偏自相关图

（4）模型预测

将选取的瓦斯浓度数据按照7∶3 的比例分割为训练集和测试集， 使用建立好的模型对测试数据集进行预测， 模型预测结果与测试样本实际值的对比情况如图4 所示。 由图4 知，预测值和实际值相差很小，ARIMA（2，1，2）模型较为准确地预测了瓦斯浓度随着时间变化情况。

图4 采用ARIMA 模型的瓦斯浓度预测值与实际值的对比

2.2 利用LSTM 模型进行预测

实验平台采用Tensorflow 框架来完成深度学习的过程， 并利用已有的数据训练出理想的LSTM 模型。 在训练模型前，为保障模型的精度，提升模型训练效率，首先要对瓦斯浓度数据进行归一化处理，归一化处理后LSTM 模型的数学表达式为

对瓦斯浓度数据进行归一化处理后， 将数据集按照7∶3 的比例划分为训练集和测试集。 LSTM 网络层通常包括输入层、隐含层和输出层3 层结构，在训练过程中， 模型的输入层节点数和输出层节点数都为1，隐含层节点数设置为4，模型训练的epochs 设置为50 轮，batch_size 设置为72， 选用Adam 优化误差。利用训练好的模型对测试集进行预测，预测结果与实际值对比见图5。

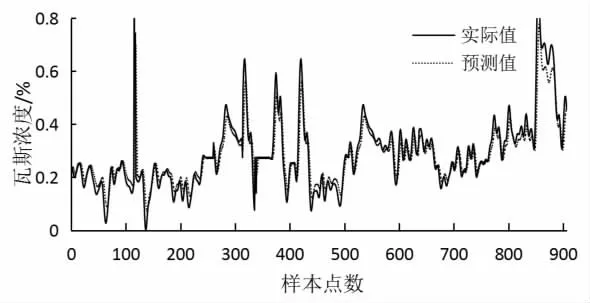
图5 采用LSTM 模型的瓦斯浓度预测值与实际的对比

3 模型评价指标

为了更好地比较ARIMA 模型和LSTM 模型的预测效果， 本文选择均方根误差 （Root Mean Squared Error，RMSE） 和 平 均 绝 对 误 差（Mean Absolute Error，MAE）两种指标来评价模型的预测准确度，其计算公式分别为

ARIMA 模型和LSTM 模型的RMSE 和MAE 见表3，由表3 可以看出，ARIMA 模型的RMSE 和MAE小于LSTM 模型的RMSE 和MAE，ARIMA 预测模型的精度略高于LSTM 预测模型，ARIMA 预测模型的预测效果更好。

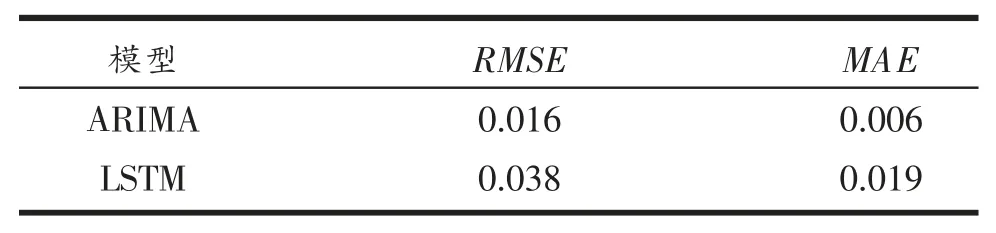
表3 不同模型预测误差对比

4 结束语

本文以山东省某矿井工作面2021 年1 月21 日至22 日瓦斯浓度值的实测数据作为样本数据，采用ARIMA 模型与LSTM 模型进行预测， 通过对比2 种模型预测结果发现，ARIMA 模型和LSTM 模型在预测瓦斯浓度方面均有良好的表现， 其中采用ARIMA模型的预测较为精准。 本文的不足之处在于仅选用瓦斯浓度单一指标进行了预测， 而瓦斯浓度会受到周围环境因素的影响，如风速、温度等，因此，下一步将考虑将瓦斯浓度及周围环境的影响因素共同加入模型，进一步提高模型预测精度。

参考文献：［1］ 孙建华，张志立，石茜，等.基于主成分-逐步回归分析法的瓦斯涌出量预测研究［J］.煤炭工程，2020，52（1)：89-94.

［2］ 李树刚，马莉，潘少波，等.基于循环神经网络的煤矿工作面瓦斯浓度预测模型研究［J］.煤炭科学技术，2020，48（1)：33-38.

［3］ 张震，朱权洁，李青松，等. 基于Python 的瓦斯浓度ARIMA 预测模型构建及其应用［J］.华北科技学院学报，2020，17（2)：23-28.

［4］ 孙卓越，曹垚林，杨东，等. 基于长短时记忆神经网络的回采工作面瓦斯浓度动态预测［J］.煤矿安全，2019，50（12)：152-157.

［5］ YANG X N， ZHANG K X， YANG H G， et al.Multiple regression and ARIMA model prediction on the yield of MSW in Xi’an［J］. Environmental sanitation engineering，2020，28（2)：37-41.

［6］ 李莎，林晖.结合MLR 和ARIMA 模型的时空建模及预测［J］.计算机工程与应用，2021，57（13)：276-282.

［7］ 王鑫，吴际，刘超，等. 基于LSTM 循环神经网络的故障时间序列预测［J］.北京航空航天大学学报，2018，44（4）：772-784.