基于共轭梯度求解代价函数的卷积码参数识别算法

陈增茂，陆 丽，孙志国，*，孙溶辰

（1.哈尔滨工程大学信息与通信工程学院，黑龙江 哈尔滨 150001；2.哈尔滨工程大学工业和信息化部先进船舶通信与信息技术重点实验室，黑龙江 哈尔滨 150001）

0 引 言

纠错编码识别技术是在缺少编码先验信息的情况下，通过一些反推方法，根据接收序列恢复出原始的编码参数，在深空通信、信息对抗等领域有着广泛的应用［1］。卷积码作为一种非常重要的纠错编码方式［2］，自1955年由Elias提出以来，一直受到广泛关注。由于卷积码具有优良的性能，其常用于构造级联码和Turbo码［3-4］，例如递归系统卷积（recursive systematic convolutional，RSC）码通常作为Turbo码的子码，正确地识别出RSC码的参数是识别Turbo码参数的关键［5］。Turbo码具有较好的纠错能力，常工作于恶劣的信道环境中［6］，这就要求卷积码参数识别算法也要具有很强的抗噪能力。但目前的研究现状不足以实现低信噪比（signal to noise ratio，SNR）下卷积码参数的盲识别，仅能在已知卷积码的码长、信息位长度、记忆长度、生成矩阵和码字起点中的一种或多种的情况下，识别出剩余参数。于是本文重点研究根据先验信息提高卷积码参数识别算法的抗噪能力。

卷积码参数识别算法根据接收序列的不同，可以分为利用解调硬判决序列的算法和利用解调软判决序列的算法。解调硬判决序列仅利用了比特符号信息，丢弃了可靠度信息，对接收信息的利用不够充分；而解调软判决序列中不仅包含比特符号信息，还包括可靠度信息，充分利用这些可靠度信息可以大大提升算法的识别性能。

利用解调硬判决序列的算法有高斯直解法、快速合冲法［7］、欧几里得法［8］、Walsh-Hadamard［9-11］变换（Walsh-Hadamard transform，WHT）法和主元消元法［12-16］等，其中WHT算法本质上是一种穷举算法，抗噪能力较强，但记忆长度的增加会导致计算量呈指数级别增大。

解调软判决序列中包含比特符号信息和可靠度信息，充分利用可靠度信息可以提高算法的抗噪能力。文献［17］提出对解调软判决序列进行识别，首次将EM（expectationmaximization）算法引入到卷积码参数识别中，但该算法的抗噪能力一般，且计算量较大。文献［18-19］提出了一种基于对数似然比（log-likelihood ratio，LLR）的卷积码参数识别方法，该算法将生成矩阵的识别问题转化成求解含错方程的问题，并且将方程成立的概率用来衡量解向量符合的程度，但对算法抗噪能力的提升有限。文献［20-21］提出用校验关系的平均似然差（likelihood difference，LD）代替LLR作为校验结果正确性的度量，降低了算法的复杂度。但是，这些算法的抗噪能力都略差于利用解调硬判决序列的WHT算法。为了进一步挖掘解调软判决序列提高算法抗噪能力的潜能，文献［22］提出了一种基于最小二乘（least square，LS）代价函数的算法，显著提高了算法的抗噪能力，但计算复杂度较高，在低SNR的环境下鲁棒性相对较弱。为了克服这些缺点，文献［23］改进了文献［22］的算法，提出了一种基于最大余弦（maximum cosinoidal，MC）代价函数的方法。该方法的计算复杂度明显降低，识别性能也有所提升，但是这些算法的抗噪能力仅与WHT方法相当甚至略差，未充分发挥出解调软判决序列可以提高算法抗噪能力的作用。

针对上述问题，本文继续研究利用解调软判决序列的卷积码参数识别算法。首先，根据编码序列和生成矩阵的约束关系构造了一个基于指数函数的代价函数模型，将生成矩阵的识别问题转换成代价函数极值的求解问题。进而，采用共轭梯度法［24］完成生成矩阵的识别。最终，通过仿真结果验证了该算法的适用性，提升了算法在低SNR下的抗噪能力。

1 卷积码识别数学模型

（n，k，m）卷积码的编码过程［25-26］用数学描述为

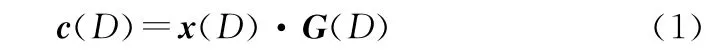
式中：x（D）＝［x0（D），x1（D），…，x k-1（D）］表示输入的k路信息序列多项式向量；c（D）＝［c0（D），c1（D），…，c n-1（D）］表示输出的n路编码序列多项式向量；m表示记忆长度；G（D）表示卷积码的生成矩阵。对于（n，1，m）卷积码，G（D）＝［g0（D），g1（D），…，g n-1（D）］。其中，D表示延迟操作。

式中：τ表示编码序列的时间长度；x i＝｛x i，0，x i，1，…，x i，τ｝表示信息序列；c i＝｛ci，0，ci，1，…，ci，τ｝表示编码序列。

对于RSC码，其编码器是反馈编码器。用g1（D），g2（D），…，g n-1（D）表示编码器的前向生成多项式，g0（D）表示反馈多项式。编码过程可以用系统反馈形式表示：

编码序列c经过数字调制等处理后，通过加性高斯白噪声（additive white Gaussian noise，AWGN）信道传输，在接收端得到的解调软判决序列为r＝（r0，r1，…，r n-1），其中r i＝｛ri，0，ri，1，…，ri，τ｝。以二进制相移键控（binary phase shift keying，BPSK）调制为例，编码信息“0”被映射成调制符号“1”，编码信息“1”被映射成调制符号“-1”，用数学形式表 示该映射过 程：si，t＝1-2c i，t。经过AWGN信道传输，接收端得到的解调软判决信息为r i，t，ri，t＝si，t＋w i，t＝1-2ci，t＋w i，t，其中w i，t表示AWGN，w i，t～N（0，σ2）。由于信道噪声与传输信号是相对独立的，因此ri，t服从均值为s i，t、方差为σ2的高斯分布：ri，t～N（si，t，σ2）。因此，ri，t具有如下形式的概率密度函数［27］：

一般情况下，发送的信息是随机的，si，t的值为“1”和“-1”的概率相同，均为1／2。在给定si，t的条件下，ri，t的概率密度函数为

根据贝叶斯定理，可以得到如下形式的条件概率密度函数：

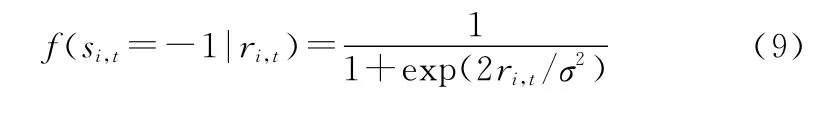
生成矩阵对应元素为1的概率用qi，l表示，则有P（g i，l＝1）（i＝0，1，…，n-1；l＝0，1，…，m）。

用q＝（q0，q1，…，q n-1）表示生成矩阵每个元素为1的概率，其中q i＝（qi，0，qi，1，…，qi，m）。求解生成矩阵的问题可以转换成q的计算。

2 卷积码参数识别算法

2.1 代价函数模型

根据式（5），可以推出：

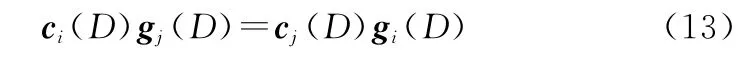
式中：i，j＝0，1，…，n-1，i≠j。

进一步可以推出

展开得

下面讨论如何利用解调软判决序列r＝（r0，r1，…，r n-1）表示式（16）。首先给出二元域中的一些结论［28］。令u1和u2是二元域中的两个独立随机变量，有

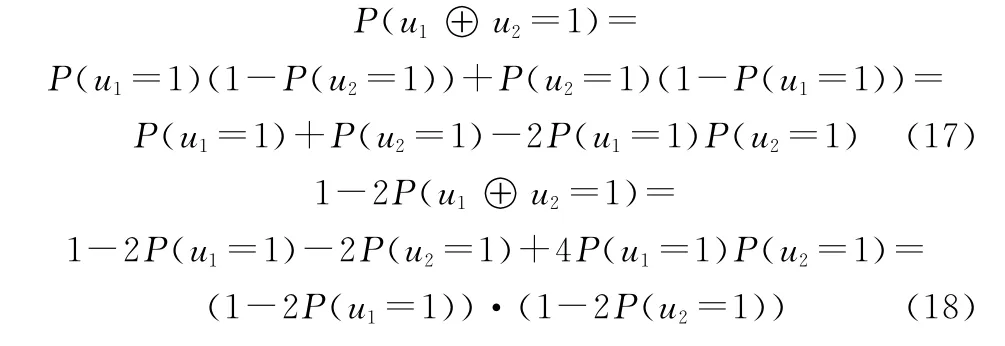
将式（18）推广，u1，u2，…，us均为二元域的独立随机变量，得

式（16）中的ci，t-u和c j，t-u是编码序列中的比特元素，取值为0或1，可当作常量；g i，u和g j，u是待识别的变量，取值也是0或1，可看作二元域中互相独立的随机变量。因此，不考 虑编码序列 中比特 间 的 相 关 性，ci，t-u g j，u和c j，t-u g i，u可视为二元域中互相独立的随机变量。故可将式（19）应用到式（16）中，可以推出：

该式是关于q的校验方程，可以用来衡量q满足该式的程度。由式（15）和式（16）可知，接收序列无误码时，与正确的生成矩阵相对应的q将使得的值为1；接收序列含误码时，q表示的生成矩阵对应元素的概率越接近正确值，校验方程的符合度越高的值越接近1。

为了更高效地估计生成矩阵，引入最优化方法的思想，利用指数函数构造代价函数模型：

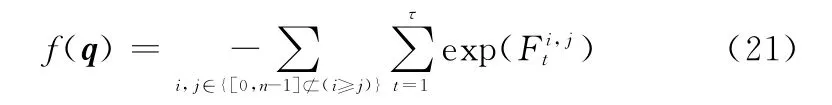
定理1当q对应正确的生成矩阵时，f（q）取极小值。

证明当q表示的生成矩阵对应元素为1的概率取值正确时，取极大值1，由于指数函数是单调递增函数，exp（）也取极大值，多个极大值进行求和取负的运算后，f（q）取极小值。证毕

于是，将生成矩阵的识别问题转化成求解f（q）极小值的问题，即

（1）g i和g j中元素为0的位置对应于c i、c j中误码出现的位置；

（2）g i和g j中元素为1的位置对应于c i、c j中含有误码的个数为奇数个。

在误码率为Pe的条件下，设其成立的概率为P0，则有：

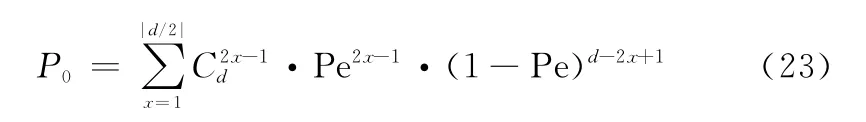
式中：d为生成矩阵g的码重；C表示组合数运算符。则

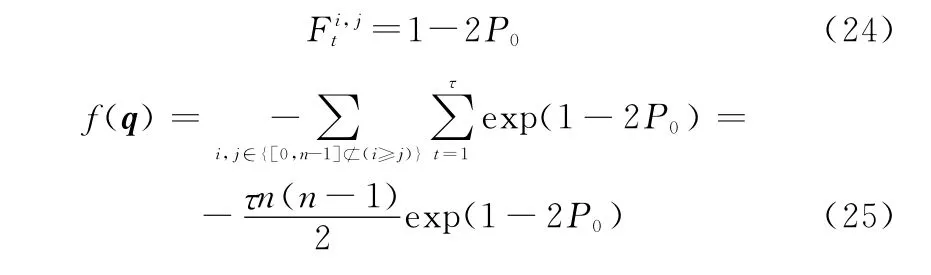
2.2 算法描述

对于代价函数的求解，采用共轭梯度法［29-30］。该方法的基本思想是在每一次迭代时利用当前点处最速下降方向-y k与算法的前一个方向d k-1的线性组合作为当前的搜索方向，即

再利用当次迭代点q k和已经确定的搜索方向计算下一次迭代点q k＋1，即

下面给出对代价函数求关于q的梯度f（q）的表达式：

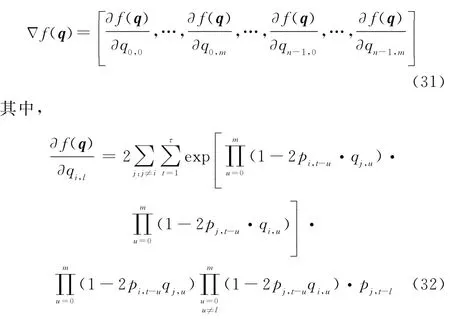
式中：i＝0，…，n-1；0≤l≤m

利用共轭梯度法求解代价函数极小值的算法步骤如下：

步骤4令k＝k＋1，转步骤1。

RSC码的生成矩阵的第一个元素一般为1，其他元素未知。因此，在迭代过程中设置q集的初始值为

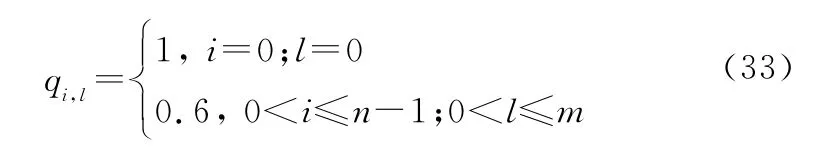
在计算过程中，会出现qi，l在［0，1］区间外的情况。当qi，l＞1时，令qi，l＝1；当qi，l＜0时，令qi，l＝0。迭代过程结束之后，当qi，l≥0.5时，令g i，l＝1；当qi，l＜0.5时，令g i，l＝0。

3 仿真实验

3.1 代价函数仿真分析

代价函数的正确性对后续生成矩阵的识别具有重要影响，故本节研究不同SNR下代价函数f（q）的变化情况，验证其正确性。分别对利用解调硬判决数据和解调软判决数据的代价函数进行仿真，并对其进行归一化处理。本次仿真中选取的卷积码的参数如表1所示，得到仿真结果如图1所示。

表1 选取的卷积码的参数Table 1 Parameters of the selected convolutional codes

图1 代价函数的变化情况Fig.1 Change of cost function

从仿真结果可以得知，随着信噪比的增加，归一化f（q）的值逐渐接近1，而无误码时归一化的值等于1。从图1中还可以看出：利用解调软判决序列情况下归一化代价函数的值与利用解调硬判决序列的值变化趋势一致，且明显大于利用解调硬判决序列的归一化f（q）值。这说明本文充分利用了解调软判决序列的可靠度信息，且构造的代价函数是正确的。

3.2 算法的影响因素分析

3.2.1α对算法识别性能的影响

α决定了算法的收敛速度，在一定程度上会影响算法的性能。正确选取α的值能够提升算法的性能。对不同α下算法的识别性能进行分析，待识别的卷积码为（2，1，6）卷积码，其生成多项式为g0（D）＝1＋D2＋D3＋D5＋D6，g1（D）＝1＋D＋D2＋D3＋D4＋D6，以下仿真中皆选用该卷积码作为实验对象。仿真过程中设置接收序列长度为4 000 bit，迭代次数为15次，蒙特卡罗实验次数为1 000次。仿真结果如图2所示。由图2可见，低SNR下，0.004≤α≤0.007时，算法的识别性能最佳，当α＞0.007时，识别正确率逐渐下降，原因在于α过小影响收敛速度，α过大易错过最佳解，故可以在仿真过程中选取α＝0.005。在后续仿真中，选取α＝0.005。

图2 α对算法识别性能的影响Fig.2 Impact ofαon performance of the proposed algorithm

3.2.2 接收序列长度对算法识别性能的影响

在某些应用领域中，需要对较小的数据量进行识别，所以接下来考察不同的接收序列长度下算法的识别性能。本次仿真中待识别的对象为（2，1，6）卷积码，设置迭代次数15次，蒙特卡罗实验次数1 000次，仿真结果如图3所示。

图3 接收序列长度对算法识别性能的影响Fig.3 Impact of the length of received sequence on performance of the proposed algorithm

由图3可见，接收序列长度对算法的识别性能有一定的影响，随着接收序列长度的增加，算法的识别性能也随之提升，在SNR＝5 dB且接收序列长度大于1 000 bit的条件下，算法的识别正确率能达到85%以上。这是由于接收的信息比特增加后，解调软判决信息也随之增加，其统计特性可以更清晰地反映信道情况和编码码元的约束关系，算法可以正确识别出卷积码参数的概率越高。

3.2.3 迭代次数对算法识别性能的影响

本节分析不同迭代次数下算法的识别性能。仿真中待识别的是（2，1，6）卷积码，接收的序列长度为4 000 bit，蒙特卡罗实验次数为1 000次，仿真结果如图4所示。

图4 迭代次数对算法识别性能的影响Fig.4 Impact of iterations on performance of the proposed algorithm

由图4可见，迭代次数达到10次时，生成矩阵基本收敛到了正确值。且在低SNR下，迭代次数对算法的影响比较明显。原因在于，信道情况较为恶劣时，每迭代一次可以更加逼近极小值，迭代次数越多，越能收敛到极小值；信道环境较好时，误码较少，迭代5次便能收敛到极小值。

3.3 算法的适用性分析

3.3.1 记忆长度m对算法识别性能的影响

本节研究记忆长度m对算法识别性能的影响。本次仿真选取n＝2的卷积码为研究对象，选择的记忆长度m分别为2、3、4、5、6，不同m对应的生成多项式如表2所示。仿真条件为：接收序列长度4 000 bit，迭代次数15次，蒙特卡罗实验次数1 000次，得到的仿真结果如图5所示。

表2 不同m对应的生成多项式Table 2 Generate matrix with respect to m

图5 m对算法识别性能的影响Fig.5 Impact of m on performance of the proposed algorithm

从仿真结果可以得知，m越大，算法的识别正确率随之降低，尤其在低SNR的情况下。这是因为随着卷积码编码记忆长度的增加，算法需要识别的参数随之增加，识别难度也随之增大。

3.3.2 码率对算法识别性能的影响

当码率变化时，需要识别的参数也会发生变化，所以码率对算法的影响也需要进行考察。本次仿真中分别对1／2、1／3、1／4码率的卷积码进行识别，不同码率对应的生成多项式如表3所示。仿真条件设置为：接收序列长度4 000 bit，迭代次数15次，蒙特卡罗实验次数1 000次，得到的仿真结果如图6所示。

表3 不同码率对应的生成多项式Table 3 Generate matrix with respect to rate

图6 码率对算法识别性能的影响Fig.6 Impact of rate on performance of the proposed algorithm

从图6中可以看出，在低SNR下，码率对算法的识别性能影响较大，SNR增加后，码率对算法的性能几乎没有影响。这是由于信道环境比较恶劣时，需要识别的参数增加必然会导致识别正确率降低；而当信道环境较好时，解调软判决序列的可靠性较高，参数增加对算法识别性能的影响较小。

3.4 算法性能对比

3.4.1 识别性能对比

本文提出的算法是基于最优化方法，目前基于最优化方法的算法有：LS算法、MC算法等，接下来对比本文算法与这些算法的识别性能。

上述算法均对解调软判决数据进行参数识别，为了全面对比算法的性能，将本文算法与利用解调硬判决数据的算法进行性能对比，其中WHT算法是识别性能最优的，故选取该算法与本文提出的算法进行对比仿真。

本次仿真中选取（2，1，4）RSC码为研究对象，其生成多项式为g0（D）＝1＋D3＋D4，g1（D）＝1＋D＋D2＋D4。仿真条件为：接收序列长度4 000 bit，蒙特卡罗实验次数1 000次，仿真结果如图7所示。仿真过程中设置本文算法的迭代次数为15次，LS算法的最大迭代次数为50次，MC算法的迭代次数为20次。

图7 本文算法与其他算法的性能对比Fig.7 Performance comparison of four algorithms

由图7可见，在-3～3 dB SNR内，本文提出的算法的识别性能明显优于其他算法。原因在于，本文构造的代价函数在极值的周围变化更加陡峭，且采用了具有Q-超线性收敛速度［30］的共轭梯度法，搜索方向更准确、搜索速度更快，避免了文献［23］中最速下降法越接近极值点迭代效果越差的情况。

3.4.2 算法复杂度对比

将本文算法的复杂度与其他算法进行比较，比较结果如表4所示。

表4 算法复杂度对比Table 4 Computational complexities of four algorithms

表4中，n表示卷积码的码长，m表示记忆长度，τ表示接受序列长度，μ表示算法的迭代次数，N表示所需Hadamard矩阵的行数，N＝2l，l≥2（m＋1）。

由表4可见，与利用解调软判决数据的算法相比，该算法的迭代次数减少，计算复杂度有所降低；与利用解调硬判决数据的算法进行对比，WHT算法的计算复杂度随着记忆长度m的增加呈指数级别增加，且占用的计算机内存较大，而本文算法呈平方级别增加，占用的计算机内存较小。

4 结 论

本文利用RSC码码元间的线性约束关系构造了一个新型的基于指数代价函数的参数识别模型，与现有的代价函数模型有所区别的是，本文构造的代价函数在极值的周围变化更加陡峭，方便搜索极值。最后，使用共轭梯度法实现代价函数极值的求解。仿真结果证明本文提出的算法收敛速度快，在迭代次数达到10次时便能收敛到最优解。与现有算法相比，该算法在低SNR下抗噪能力更强，且保持较低的计算复杂度。但本文目前只讨论了一些记忆长度较短的卷积码，如何在记忆长度较长时确保较强的抗噪能力和低计算复杂度，将作为下一步的研究工作。