基于特征值高阶矩的频谱感知增强技术

李 贺，赵文静，金明录，*

（1.大连理工大学信息与通信工程学院，辽宁 大连 116024；2.电子科技大学信息与通信工程学院，四川 成都 611731）

0 引 言

随着物联网等技术的快速发展，大量无线设备接入导致对频谱资源的需求呈爆炸性增长。固定频谱分配策略对频谱资源使用效率低，难以满足日益增加的频谱需求［1-4］。因此，未来无线通信需通过扩展通信频谱范围（至毫米波频段）及动态频谱共享技术（认知无线电技术）解决频谱资源匮乏及频谱利用率低的问题［5-9］。

认知无线电技术通过频谱复用或频谱共享提高频谱利用率。在认知无线电网络中，当主用户没有利用其授权频谱时，认知用户可以通过该频谱进行通信。为了实现该目的，认知用户需要对主用户的授权频段的占用状态进行确认，即检测主用户信号存在与否，该过程称为频谱感知。当主用户正在使用当前授权频段时，为了不对主用户产生干扰，认知用户需要以较高的检测概率判断主用户的激活状态，并在一定的时间内清空信道或降低传输功率。因此，设计高效可靠的频谱感知技术一直是实现认知无线电技术的重中之重［10-14］。

目前，频谱感知方法主要分为最优检测、半盲检测及盲检测方法3类。这些方法在不同的实现条件及要求下具有不同的性能。众所周知，匹配滤波方法是最优检测的代表。然而，其最优性能是以每一个认知用户满足同步，且已知主用户和噪声的先验信息为先决条件，这些因素限制了该方法在实际场景中的应用［15-17］。

与最优检测算法相比，半盲检测算法只需已知噪声功率。能量检测（energy detection，ED）算法是典型的半盲检测算法［18-21］。ED算法不需要主用户的先验信息且易于实现。ED算法对于独立同分布信号具有最优的检测性能，但对于相关信号的检测性能下降。在实际场景中，信号功率由于多径衰落及遮蔽现象产生波动，造成信噪比低，进而导致ED算法的性能严重退化。此外，实际噪声随时间不断变化，产生噪声不确定性问题，使得ED算法的虚警概率大幅提高。

为了解决这些问题，一些不依赖于信号和噪声先验信息的全盲检测算法被相继提出。例如，基于特征值的检测算法通过利用信号间的相关性提高了检测概率［22-23］。典型的特征值检测算法包括最大最小特征值（maximum-minimum eigenvalue，M ME）检测算法［22］、最大特征值 算术平均值（maximum eigenvalue to the arithmetic mean，ME-AM）检测算法［24-25］、最大特征值 几何平均值（maximum eigenvalue to the geometric mean，ME-GM）检测算法［26］等。由于协方差矩阵的特征值能够较好地捕捉信号的相关性及噪声特性，这几种算法在低信噪比下具有较好的检测性能，且能克服噪声不确定问题。

这些基于特征值的检测算法设计依赖于随机矩阵理论和样本协方差矩阵的特征值特性［27］。文献［28］及其参考文献表明，使用特征值的高阶矩可以提供额外的鉴别信息进而能够改善统计推断问题的性能。Sedighi等基于分离函数估计测试框架，利用样本协方差矩阵特征值的高阶矩，提出了两个全盲特征值检测器［29］。Huang等基于随机矩阵理论，提出了一种特征值矩比（eigenvalue moment ratio，EMR）的频谱感知方法［30］。这些算法均表明利用特征值的高阶矩有利于提高信号检测问题的性能。

本文将从经典的ME-AM 算法开始，研究了基于特征值高阶矩的新的检测算法设计问题。利用所有特征值的p阶矩，本文提出了新的基于特征值高阶矩的频谱感知增强算法，并给出了虚警概率和判决门限的解析表示，通过仿真实验分析了特征值高阶矩幂次p的变化对检测性能的影响，仿真结果表明了新的基于特征值高阶矩的频谱感知增强技术的有效性。

1 系统模型

图1展示了多天线认知无线电网络中的典型场景，其中有P个单天线主用户（primary user，PU），1个配有M个接收天线的认知用户用于感知主用户是否存在。图中还包含次用户（secondary user，SU）。

本质上，频谱感知问题是对主用户信号的检测，不失一般性，对于主用户的感知问题可以转化为如下的二元假设检验问题：

式中：H0表示主用户信号不存在；H1表示主用户信号存在；sj为第j个主用户发送的信号，w m（n）为噪声，其服从均值为0，方差为的高斯分布，即w m（n）～CN（0）；hmj为认知用户的第m个接收天线与第j个主用户之间的信道响应；D p为信道阶数。

第n个采样时刻的数据表示为

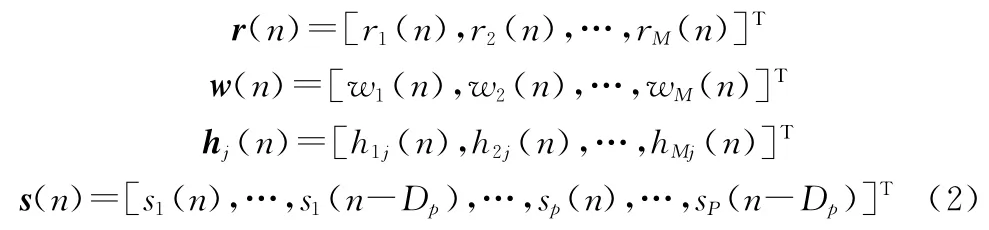
接收向量可以表示为矩阵形式：

考虑N个采样序列，接收信号的样本协方差矩阵可以表示为

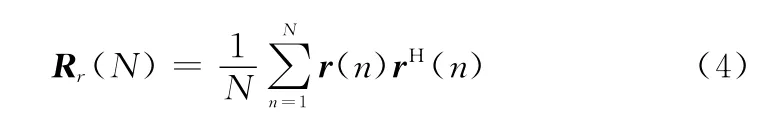
2 基于特征值高阶矩的频谱感知算法

本节首先简单介绍几种典型的基于特征值的频谱感知方法，然后利用特征值检测的优势提出了新的特征值检测方法。

2.1 经典的频谱感知方法

全盲检测算法因不依赖于信号和噪声功率信息而受到广泛关注，其中ME-AM 和ME-GM 检测方法是两种典型的盲感知方法。

（1）最大特征值与特征值的算术平均方法

针对噪声功率及信道未知情况，文献［24］利用广义似然比准则（general likelihood ratio test，GLRT）推导了基于特征值的检测算法，其检测统计量表示为

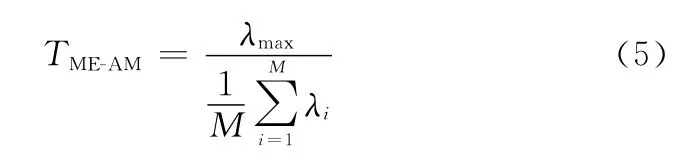
式中：λi表示样本协方差矩阵的特征值；λmax为最大特征值。仿真实验表明ME-AM检测方法在瑞利衰落信道下具有比MME等方法具有更好的检测性能。

（2）最大特征值与特征值的几何平均方法

ME-AM算法是在假设信道状态服从瑞利分布条件得出的，当该条件不满足，其性能受到影响。对此，为了提高认知用户在其他信道状态下对主用户信号的检测能力，一些检测方法应运而生。例如，文献［18］针对Nakagami-m衰落信道设计了ME-GM方法。ME-GM检测方法的检测统计量表示为

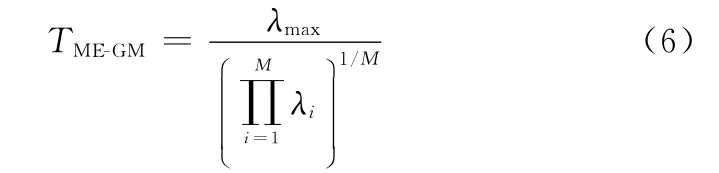
（3）基于特征值矩的典型方法

文献［29-30］提出了基于特征值矩的检测算法，其检验统计量表示如下：

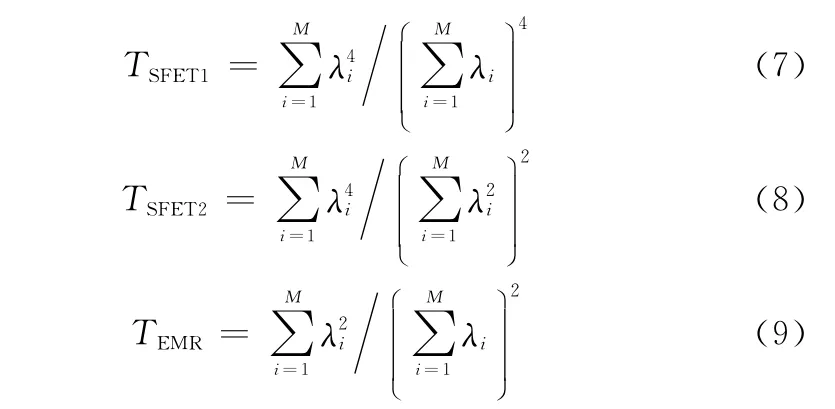
2.2 基于特征值高阶矩的频谱感知增强技术

使用特征值的高阶矩可以提供额外的鉴别信息来改善统计推断问题的性能。因此，本文考虑基于特征值的p次幂的检测算法，称为MEp-AM检测算法，其检验统计量为

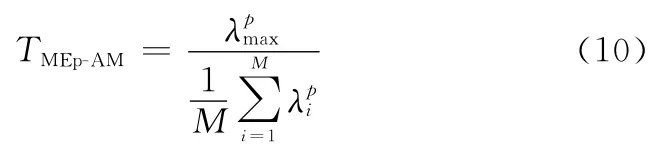
式中：0＜p＜∞。

在H0假设下，式（10）中的检测统计量理论上趋于1，而在主用户信号存在时，式（10）中的统计量大于1。因此，可以利用式（10）中的统计量判断主用户信号存在或不存在。

从式（10）可以看出，MEp-AM检测算法是ME-AM 检测算法的扩展形式，当p＝1时，MEp-AM 算法为ME-AM检测算法。

所提算法的具体过程如下：

（1）根据式（4），计算样本协方差矩阵。

（2）求解R r（N）的特征值λi（R r（N）），并计算特征值的p次幂。

（3）基于式（10）计算检测统计量，并将其与门限进行比较判断主用户信号是否存在：当检测统计量大于门限时，则表示H1成立，即主用户处于激活状态；否则，表示H0成立。

下文主要分析所提统计量TMEp-AM的统计分布，进而推导所提算法的检测概率、虚警概率和门限的解析表达式。从式（10）可知，MEp-AM检测算法的检测统计量依赖于样本协方差矩阵特征值的p次幂。当p为正整数时，文献［30］基于随机理论给出了特征值p次幂的渐近分布。当p为分数时，样本协方差矩阵的特征值任意p次幂的渐近波动很难确定，目前没有文献给出特征值分数次幂的统计分布。因此，本文利用广义极值分布拟合所提统计量的统计分布。

三参数的广义极值分布函数表示如下：

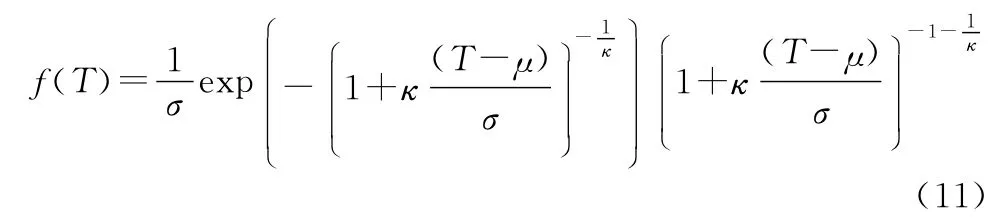
其中，μ，σ和κ分别为广义极值分布的位置参数、尺度参数和形状参数。

广义极值分布的累积分布函数表示为

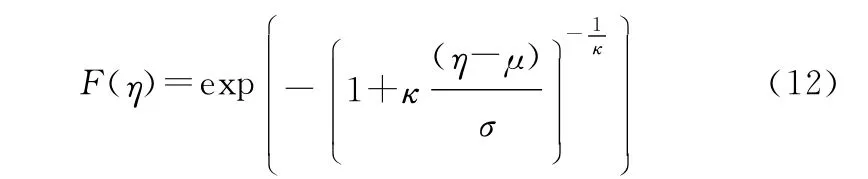
图2给出了当p分别为0.25，1，2，4时的所提统计量的经验分布与拟合的广义极值分布。从图2可以看出，经验分布与拟合分布几乎重叠，这说明了广义极值分布可以较好地近似所提统计量的统计分布。

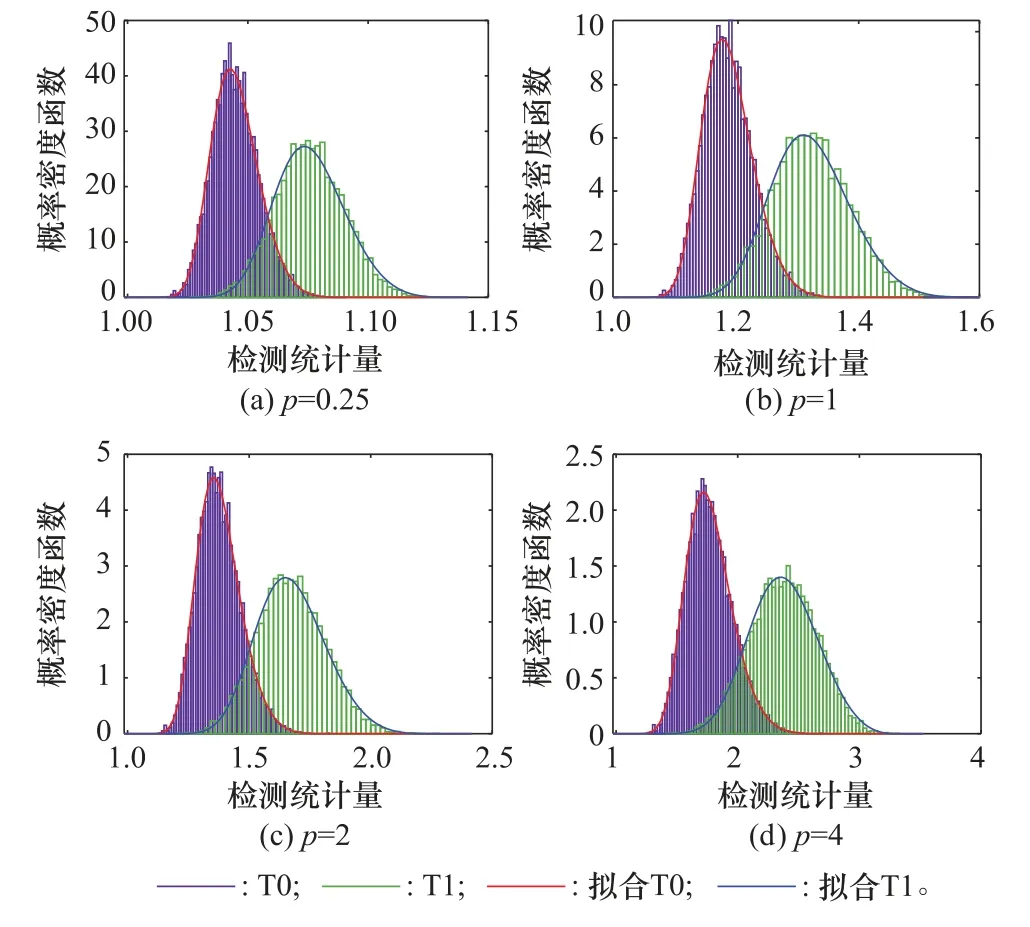
图2 检验统计量的经验分布与拟合分布Fig.2 Empirical distribution and fitting distribution of test statistics

基于广义极值分布，推导分析了所提算法的虚警概率、检测概率和门限的解析表示。

虚警概率表示为

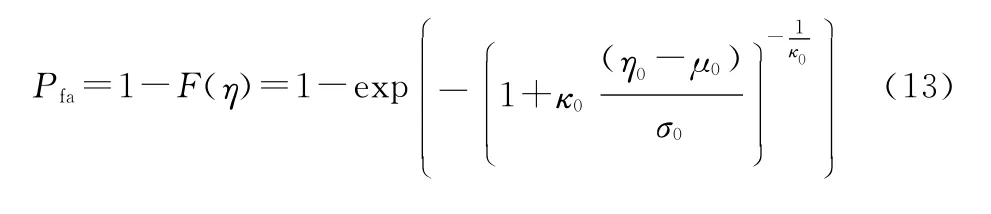
式中，μ0，σ0和κ0为H0下的估计参数。

利用虚警概率与门限的关系，可以得出门限的解析表达式：

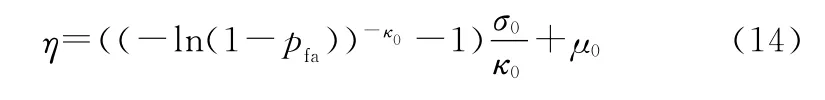
类似于虚警概率推导，检测概率表示为

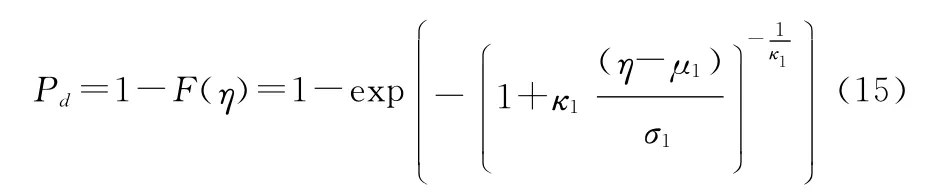
式中：μ1，σ1和κ1为H1下的估计参数。

3 实验结果及分析

本节通过仿真实验验证了所提MEp-AM算法的有效性。本文的一些仿真参数的设置与已有文献类似，假设每个主用户独立发送二进制相移键控（binary phase shift keying，BPSK）信号，认知用户接收天线数为4，采样点数设为100，在每个设定的信噪比下进行10-000次蒙特卡罗仿真。

以p＝0.1，0.25，1，2为例，首先验证了所给出的理论虚警概率和检测概率的解析表示的正确性，结果如图3所示。从图3可以看出，理论计算与仿真结果差异较小，这说明了式（13）～式（15）给出的理论计算的正确性。

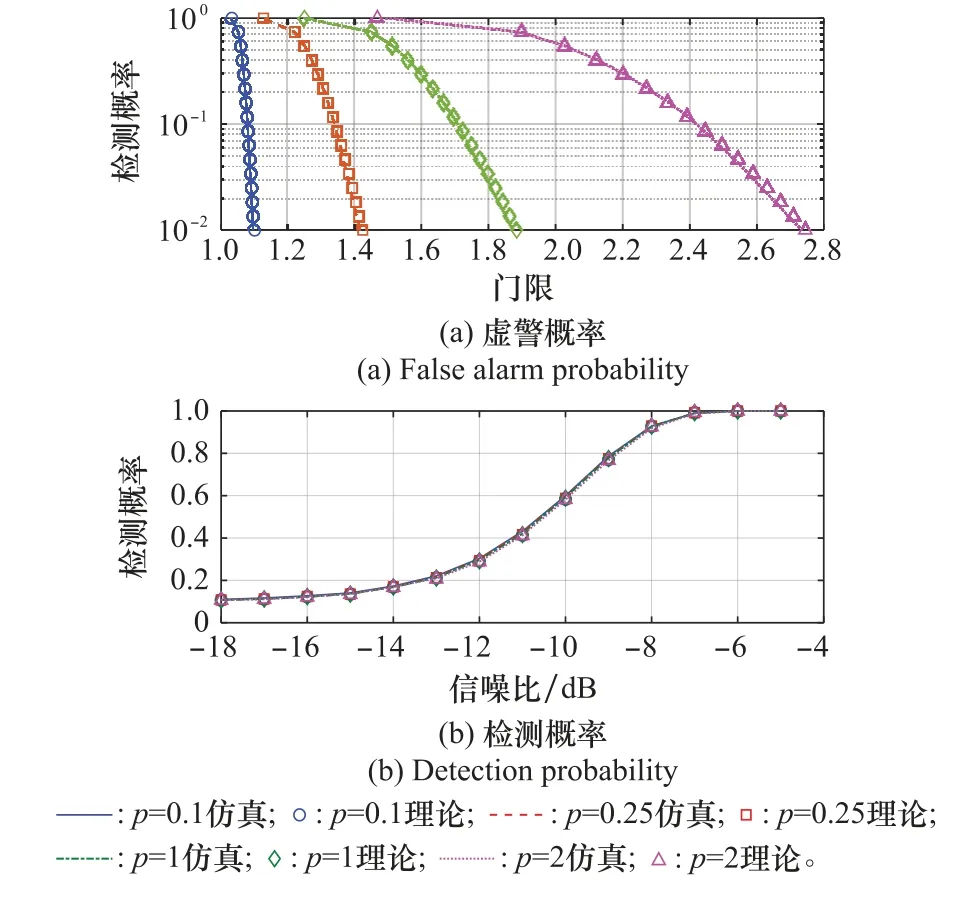
图3 所提算法的理论虚警概率、检测概率与仿真虚警概率、检测概率的比较Fig.3 Comparison between theoretical false alarm probability and simulational results of the proposed algorithm.

因为ME-AM算法和ME-GM算法分别在瑞利平坦衰落和Nakagami-m平坦衰落信道上显示出检测优势［31］，下面分别考虑这两个信道场景进行仿真。仿真实验中考虑复高斯白噪声。虚警概率设为0.1，其是WRAN 802.22工作组规定的最大许可值。为保证比较的公平性，仿真中判决门限均根据虚警概率仿真确定。特征值的p次幂设置为p＝｛0.1，0.25，0.5，1，1.5，2，4，10｝。

3.1 瑞利平坦信道下的仿真

本文主要与文献［29-30］中的基于特征值高阶矩算法、ME-GM 和MME 算法进行对比。图4～图7 中SFET1、SFET2和EMR分别代表由式（7）、式（8）和式（9）的检验统计量设计的检测算法。

首先，针对1个主用户的场景下的检测概率随信噪比变化情况进行了仿真，结果如图4所示。从图4的结果可以看出，这些算法的检测性能相差不大。但放大的子图表明MEp-AM算法在p＝0.25时检测性能最好，其次是ME-GM和ME-AM算法。此时，高阶矩的其他算法没有显示出优势。

图4 1个主用户时算法在瑞利衰落信道下的检测性能比较Fig.4 Detection performance comparison of several algorithms for the scenario with one primary user and Rayleigh fading channel

图5给出了3个主用户场景下的仿真结果。当主用户个数为3时，经典的高阶矩检测算法显示出检测优势，其次是ME-GM检测算法和MEp-AM 检测算法。因为在此场景下，接收信号样本协方差矩阵的特征值出现了分散，因此利用所有特征值的经典高阶矩检测算法显示出其检测优势。

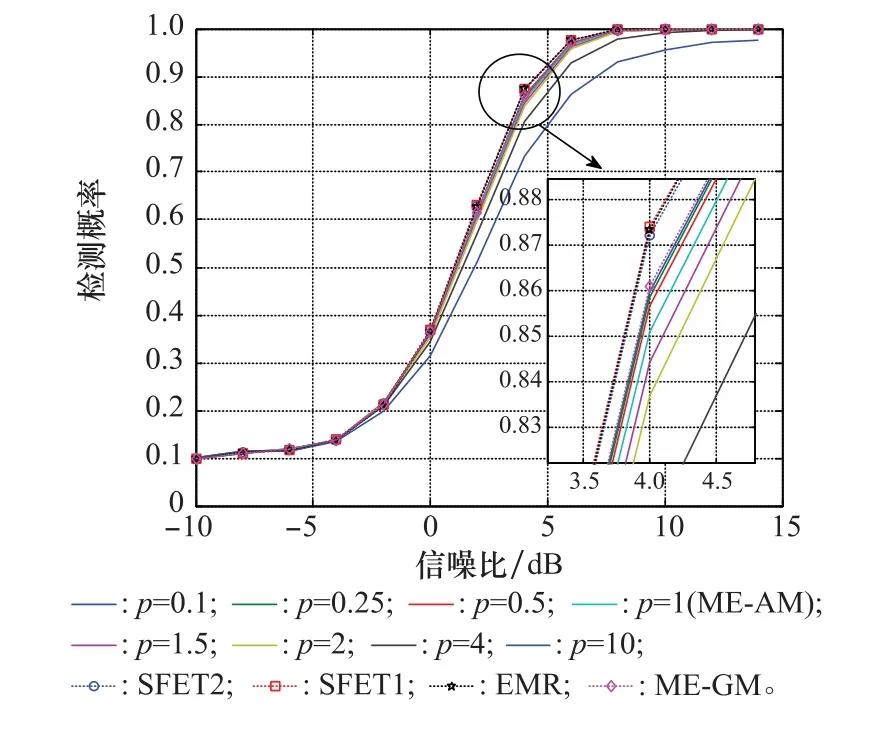
图5 3个主用户时算法在瑞利衰落信道下的检测性能比较Fig.5 Detection performance comparison of several algorithms for the scenario with three primary users and Rayleigh fading channel

3.2 Nakagami-m平坦信道下的仿真

对于Nakagami-m平坦衰落信道，其信道系数h服从如下分布：

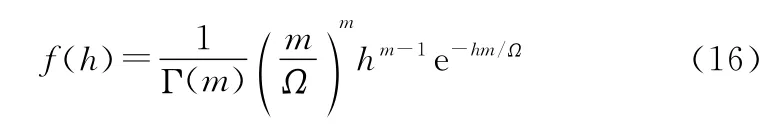
式中：m为信道衰落系数，设为1；Ω为平均信噪比。

图6给出了1个主用户场景下的仿真结果。与瑞利平坦信道情况类似，此时MEp-AM（p＝0.1，0.25）、ME-GM和ME-AM算法比经典高阶矩检测算法检测性能略显优势。

图6 1个主用户时算法在Nakagami-m衰落信道下的检测性能比较Fig.6 Detection performance comparison of several algorithms for the scenario with one primary user and Nakagami-m channel

当主用户个数为3时，几种算法的检测概率随信噪比变化情况如图7所示。与瑞利平坦衰落情形类似，经典的高阶矩检测算法显示出其检测优势，其次是ME-GM 检测算法、MEp-AM（p＝0.1）检测算法和ME-AM检测算法。

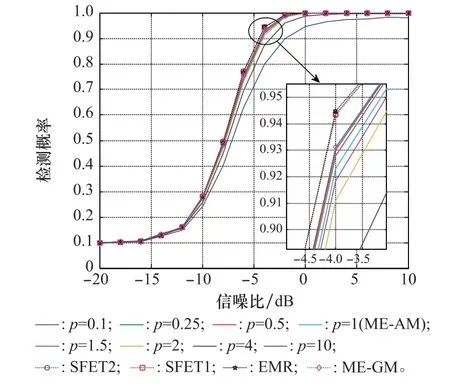
图7 3个主用户时算法在Nakagami-m衰落信道下的检测性能比较Fig.7 Detection performance comparison of several algorithms for the scenario with three primary users and Nakagami-m channel

4 结 论

基于特值的检测算法设计依赖于使用随机矩阵理论和样本协方差矩阵的不同特征值性质。本文从经典的ME-AM算法出发，提出了新的基于特征值高阶矩的频谱感知增强算法，基于随机矩阵理论，推导了所提算法的虚警概率和判决门限的解析表示，通过仿真研究了特征值高阶矩幂次的变化对检测性能的影响，仿真结果表明了所提算法的有效性。因为样本协方差矩阵的特征值任意p次幂的渐近波动很难确定，MEp-AM 的检测性能还不能从理论上进行分析，这也是今后的研究课题。