重叠网格中割补法的改进及应用
陈小毛, 宣传伟
(1.南京航空航天大学 无人机研究院,江苏 南京 210016; 2.上海宇航系统工程研究所,上海 201100)
由于精度高、逻辑关系简单、流场计算效率高等特点,结构网格技术是计算流体动力学(computational fluid dynamics,CFD)的首选技术。但是,复杂外形流场结构网格的生成是一项费时并需要经验积累的工作。重叠网格技术[1]将计算域划分为若干个简单的子域,针对各个子域单独划分网格,从而大大降低了结构网格的生成难度,同时保证了网格生成质量,也提高了网格生成效率。因此,结构重叠网格技术得以广泛应用于复杂外形流场[2]及多体相对运动[3]数值模拟中。结构重叠网格技术的核心是“挖洞”,即确定各子域网格之间的插值关系并剔除不需要计算的网格。洞面优化[4]则是针对“挖洞”的一种优化技术,其目的是改善重叠区域,使得网格重叠区域最小、插值边界远离物面,提高流场求解精度。
重叠网格技术是求解复杂外形流场及多体相对运动问题的有效途径,而准确高效的洞面优化方法是其关键技术之一。常用的洞面优化方法包括阵面推进技术[5]、隐式挖洞技术[6]以及割补法[7]。阵面推进技术是利用2个阵面反复迭代推进挖洞面来进行重叠网格挖洞的过程。阵面的推进距离依赖于阵面和相邻网格点之间的相对距离,且一定程度上需要人工操作,自动化程度稍低。隐式挖洞技术是一种基于网格单元品质的插值单元选择方法[8]。该方法没有单独的初始挖洞过程,仅仅需要寻找最佳品质的贡献单元即可[9],因此网格装配效率和自动化程度较高。但正是由于挖洞过程的缺失,插值单元可能出现在物体内部,从而影响计算结果[10]。作为阵面推进技术的改进方法,割补法以洞边界点为起点,沿着网格线离散地做推进运动,每段网格线的长度即为该次推进的距离。与阵面推进方法相比,割补法的迭代推进次数少,自动化程度高,因此得到了较好的发展。但是,割补法仍然存在如下2个问题:一是当壁面距离很近时,割补法的填补过程容易因少数洞边界点找点过程的失败而导致网格进入壁面内;二是割补完后洞边界的位置不可预测,洞边界参差不齐。针对第1类问题,文献[11]提出了Volume Method和Vertex Method 2种方法。其实质是去掉填补过程,将割补法的2个过程变为1个过程。但由于网格体积的非单调性,Volume Method可能会导致单元属性转换混乱,出现网格孤岛。文献[12]通过引入2类洞内点概念,使得位于另一物体内部的网格点的属性在填补过程中不被修改,同样解决了狭缝重叠中洞边界易挖进物面的问题。文献[13-14]提出将割补法与物面距准则[15]相结合的方法解决了第2类问题,该方法在网格割补之前增加了一个以物面距离为准则的网格分类过程。
针对割补过程中产生的2类问题,本文在网格切割过程中将物面距离作为判别标准。与文献[14]不同,本文方法仅在切割过程中搜索洞边界点的贡献单元,避免了对全局所有网格点进行贡献单元的搜索,提高了网格装配效率。当洞边界点的物面距小于或等于其贡献单元的物面距时停止切割,从而使得洞边界处于壁面中间位置;在网格填补过程中,以切割结束时的洞边界作为初始阵面进行网格回填,直至产生两层插值边界。本文首先对传统割补法进行简单介绍,然后详细阐述改进后的割补法过程,最后通过2个典型流动算例验证本文所提方法的可靠性。
1 割补法
挖洞和贡献单元搜索是结构重叠网格技术的2个关键过程,而其中的挖洞过程本质上是一个将网格节点分类的过程,即直接参与流场计算的点为正常点,不参与计算的点为洞内点,参与插值计算的点为洞边界点。挖洞又可以细分为初始挖洞和洞边界优化2个步骤。初始挖洞旨在标记出所有落入物体内部的网格点,从而不参与流场计算。割补法在初始挖洞的基础上,经过“切割”和“填补”2个阶段,使得各子网格间的洞边界最优化。贡献单元的搜索也在该过程中完成。
1.1 切割过程
经过初始挖洞之后的网格重叠区域通常十分巨大,洞边界可能位于流场梯度较大的边界层内,流场计算精度低。在该阶段,所有洞边界点依次寻找贡献单元。若贡献单元的所有节点都为正常点,则该洞边界点转变为洞内点,与其相邻的正常点转变为洞边界点,由此将洞边界推离物面;若贡献单元的节点不全为正常点,则停止该过程。
1.2 填补过程
经切割之后,没有网格单元重叠,而填补阶段本质上是切割阶段的逆过程,其目的是将洞边界逐步收缩从而实现网格单元的重叠。在该阶段,所有洞边界点依次寻找贡献单元。若贡献单元的节点不全为正常点,则该洞边界点转变为正常点,与其相邻的洞内点转变为洞边界点,由此收缩洞边界,直至再无洞内点转变为洞边界点。
割补法过程示意图如图1所示,图1中:N表示正常网格点(normal point),参与流场计算;H表示挖去的洞内点(hole point)不参与计算;F表示洞边界点(fringe point),用于插值计算。

图1 割补法过程示意图
2 割补法的改进
在网格切割过程中,洞边界的推进是按照网格线来进行的,因此最终洞边界的位置严重依赖于网格单元尺度在各方向上的分布特征。对于同一个问题,经过割补后,不同的网格可能会产生不同的洞边界;而且当网格匹配性较差时,洞边界甚至可能深入物面边界层,从而降低插值精度。另外,洞边界在空间上的分布也会参差不齐[14],如图2所示,机翼和油箱分离模型经过割补后,洞边界靠近物面而且参差不齐。

图2 割补法洞边界参差不齐现象
在网格填补过程中,当物面距离很近时,填补过程容易由于少数洞边界点的寻点过程失败而导致网格进入物面内部,如图3所示[12]。

图3 割补法的缝隙问题
针对上述2种问题,本文对传统割补法进行改进,具体步骤如下:
(1) 物面距计算。将所有网格点标记为正常点,并计算所有网格点的物面距(若该点属于背景网格,则将其物面距离设置为一个大值)。
(2) 初始挖洞。使用洞映射法[16]对所有网格进行挖洞(洞边界位于物面处),将位于物面内部的网格点标记为洞内点,与洞内点相邻的正常点标记为洞边界点。
(3) 切割。针对所有洞边界点,进行ADT[17]寻点操作,搜索并保存其贡献单元信息,通过三线性插值法得到贡献单元的物面距。比较该洞边界点与其贡献单元的物面距大小。若前者大于后者,则将该洞边界点标记为洞内点,而与其相邻的正常点标记为洞边界点。
(4) 循环步骤(3),直至所有洞边界点的物面距小于或等于其贡献单元的物面距。
(5) 填补。将与洞边界点相邻的2个洞内点标记为插值点,然后将该洞边界点标记为正常点。
本文方法的过程示意图如图4所示,该套网格系统由4块子网格和1块背景网格组成。每块子网格包含3 960个网格点,背景网格包含42 411个网格点。以物面边界为初始挖洞边界的结果如图4a所示,从图4a可以看出,位于物面内部的网格均已被挖去,将已被挖去的网格点标记为洞内点,即上述步骤(2)。将与洞内点相邻的正常点标记为洞边界点对应步骤(3)、步骤(4),使用ADT方法循环搜索洞边界点的贡献单元,比较洞边界点与其贡献单元的物面距大小,更新洞边界,直至所有洞边界点的物面距小于或等于其贡献单元的物面距,结果如图4b所示。此时,洞边界位于物面中间位置。为保证二阶计算精度,对应上述步骤(5),将与洞边界点相邻的2个洞内点标记为插值点,如图4c所示。

图4 改进型割补法过程
针对上述网格系统,本文方法与文献[14]方法的效率对比情况见表1所列。文献[14]方法需要搜索所有网格点的贡献单元,因此需要进行寻点操作的网格点数为所有子网格点数目之和,即58 251个。而本文方法的寻点操作是在网格切割的同时进行的,且只需对洞边界点进行寻点操作,累计点数为6 582个,明显少于文献[14]方法,耗时不足其1/2,具有更高的效率(本文所有计算均基于Intel Xeon CPU E5-2650平台,主频为2.00 GHz)。

表1 不同方法效率对比
如前所述,针对三段翼网格系统,当缝翼与主翼网格很近时,在填补过程中传统割补法往往会因少数洞边界点的寻点过程失败,而导致洞边界进入物面内部(见图3)。使用本文方法对其进行重叠网格装配的效果如图5所示。由于切割过程中保存了所有洞边界点的贡献单元信息,因此填补过程可不用搜索贡献单元,从而避免了壁面距离很近时因少数点的贡献单元搜索失败而导致整个网格重叠过程失败的可能性。从图5可以看出,洞边界位于缝翼和主翼面中间,而且主翼面网格也没有进入缝翼内部。

图5 缝翼距离主翼很近时重叠网格效果
S300C型旋翼结合Robin机身重叠网格系统如图6所示。

图6 旋翼机身重叠网格系统
该套网格系统由如下5个部分组成:背景网格、Robin机身网格、3个S300C旋翼网格,共3 588 672个单元。使用本文方法对其进行网格装配后的效果如图7所示,不同子网格间插值边界分布正确、合理。本文方法与文献[14]方法效率对比情况见表2所列。从表2可以看出,本文方法具有更高的效率。

图7 挖洞效果

表2 旋翼机身网格不同方法效率对比
3 数值模拟
3.1 计算方法
本文采用有限体积法对Navier-Stokes控制方程进行离散求解,空间离散采用Roe-FDS(flux difference splitting)格式,具备二阶空间离散精度;湍流模型采用SST模型;时间离散采用LUSGS(Lower-Upper Symmetric Gauss-Seidel)隐式计算方法。
3.2 30P30N三段式机翼
对经典的二维三段式机翼30P30N[18]进行数值模拟。来流马赫数Ma=0.2,雷诺数Re=8.7×106,攻角α=8°。流场网格由以下4个部分组成:缝翼网格为300×101、主翼面网格为682×151、襟翼网格为300×141、背景网格为609×600。经洞面优化后重叠效果如图8所示,重叠网格的洞边界清晰整洁,位于不同翼面的中间位置。翼面压力云图和等马赫线如图9、图10所示。从图9、图10可以看出流场分布合理,重叠边界处等马赫线和压力线过渡光滑。翼面压力系数的数值与试验结果对比如图11所示。图11中:Cp为压力系数;x/c为x坐标与弦长c的比值。计算结果与试验值[19]吻合良好,表明本文洞面优化方法准确可靠。

图8 30P30N机翼重叠网格效果图

图9 30P30翼面压力云图

图10 30P30翼面等马赫线

图11 30P30N翼面压力系数计算值与试验值对比
3.3 Titan Ⅳ运载火箭
为进一步验证本文方法在三维复杂外形流场中的适用性,对美国大力神Titan Ⅳ运载火箭[20]超音速外流场进行了数值仿真。TitanⅣ运载火箭采用并联式布局,芯级和助推级距离较近,是典型的狭缝重叠问题。Titan Ⅳ火箭重叠网格系统如图12所示,由以下3个部分组成:芯级网格、2个助推器网格,共 4 905 743个六面体单元。采用本文方法进行挖洞后的效果如图13所示。从图13可以看出,洞边界整齐合理,位于物面中间,且不存在狭缝问题。

图12 Titan Ⅳ重叠网格系统
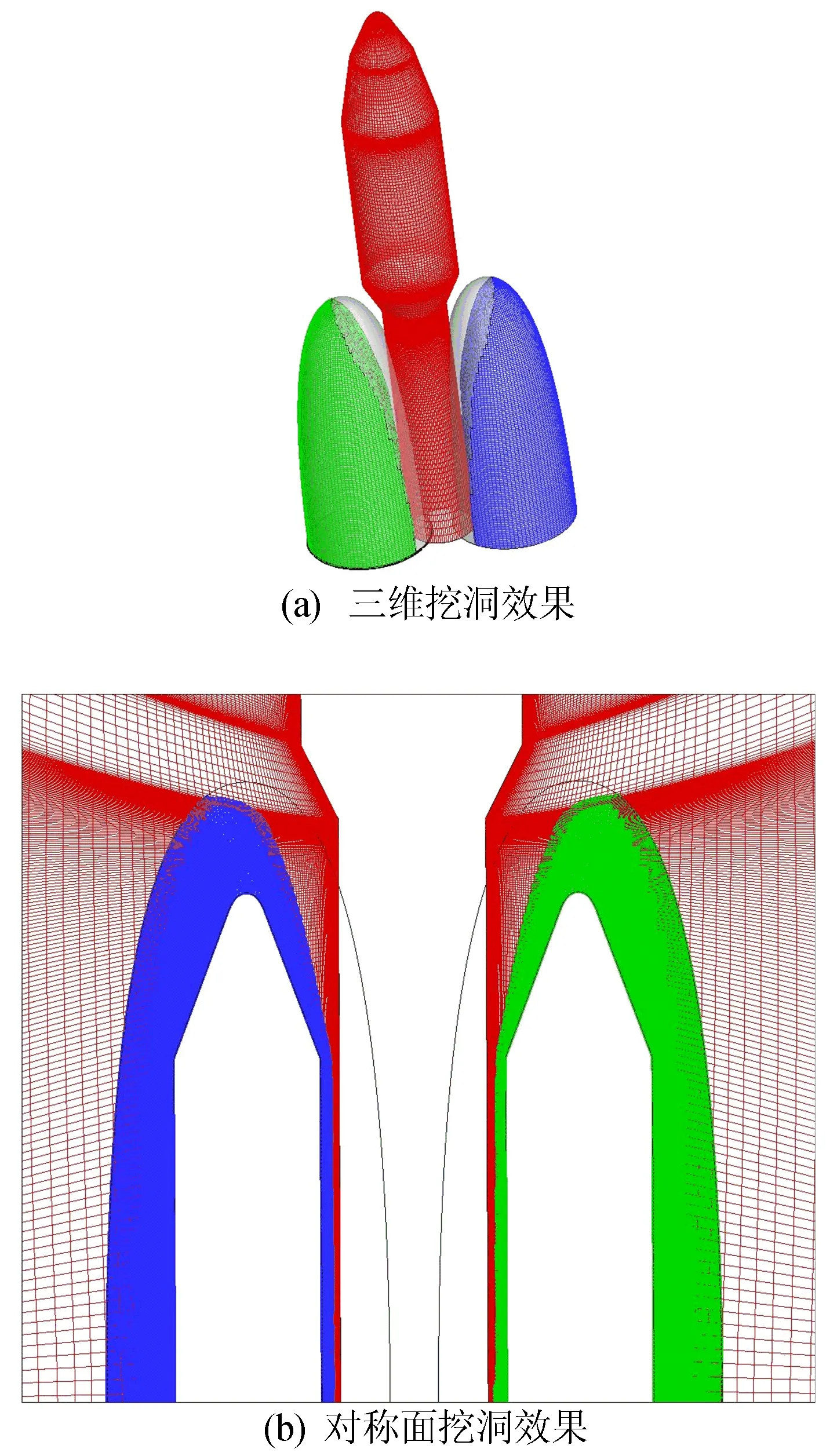
图13 Titan Ⅳ挖洞效果
本算例计算条件为:马赫数Ma=1.6, 攻角α=0°,雷诺数Re=115×107。对称面流场马赫数分布如图14所示。芯级中心线压力数值结果与试验值的比较结果如图15所示。

图14 Titan Ⅳ对称面马赫数云图

图15 芯级中心线压力分布
图15中:p为芯级中心线压强;pref为来流远场压强;x为沿芯级中心线位置;r为芯级半径。从图14、图15可以看出,网格重叠区域等压线分布合理、光滑, 计算结果与试验值吻合得很好。由于芯级与助推级之间存在连接机构, 导致试验的峰值点略高,且在连接机构附近数值结果与实验值之间的偏差稍大(图15中,x/r值在25~35之间的区域)。本文所涉及的4种模型分别采用本文方法与文献[14]方法进行重叠网格装配效率对比,结果如图16所示。图16中:横坐标表示4种模型编号;纵坐标表示网格装配所用时间。从图16可以看出,本文方法具有更高的效率,且随着网格数目的增多,本文方法具有更明显的效率优势。
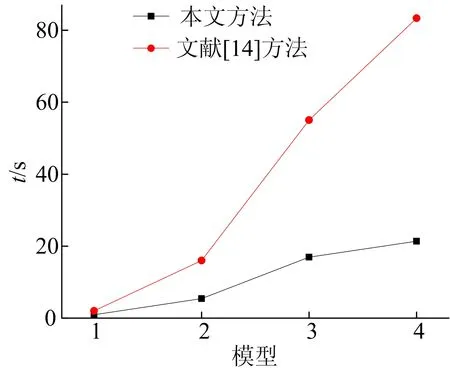
图16 4种模型采用不同方法的效率对比
4 结 论
本文针对传统割补法的狭缝问题和洞边界位置不可预测性问题,发展了一种改进型洞边界优化方法。
(1) 通过将壁面距离作为网格切割过程的判别标准,使得洞边界位于物面中间,解决了传统割补法洞边界不可预测且参差不齐的问题。
(2) 相比文献[14]方法,本文方法更简洁,在网格切割过程中只需搜索当前洞边界点的贡献单元,避免了搜索所有网格点的贡献单元,具备更高的网格装配效率。
(3) 在网格填补过程中,由于不需要再次搜索贡献单元,因此解决了因少数洞边界点找点过程的失败而导致网格进入物面内的问题。与文献[11]的Volume Method方法相比,由于本文方法未涉及到网格体积大小,因此不存在“孤点”问题,具有更好的鲁棒性。
(4) 通过经典算例验证了本文方法的准确性与可靠性。

