基于热传导的多片离合器温度特性分析与结构优化

胡 芳, 姜武华, 梁修天

(1.合肥工业大学 研究生院,安徽 合肥 230009; 2.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)

电控限滑差速器可以使车辆在转弯等工况下更好地匹配左右轮的驱动转矩,不仅可以提高车辆的动力性和特殊路况的通过性,还可以改善车辆的安全性和操纵稳定性[1-2]。多片离合器依靠摩擦片之间的摩擦将动力按照控制目标主动地分配到左右车轮[3],是电控限滑差速器动力传递的关键部件,对多片离合器性能的研究显得尤为重要。文献[4]以多片离合器的带排转矩最小为优化目标，建立油槽结构与工作参数优化模型实现对油槽数量和深度的优化;文献[5]利用SAE#2试验台进行多组试验,发现在润滑条件下,摩擦转矩衰减趋势随着相对转速的增大逐渐减小,随着摩擦副压力的增大而增大;文献[6]建立包含花键摩擦力的多片离合器转矩计算模型,并通过试验验证了模型的准确性。摩擦片与对偶钢片摩擦的同时会产生大量的热,这一过程对多片离合器性能、润滑油性能都产生了一定的影响;文献[7]通过搭建接合传热过程的有限元模型,分析了摩擦元件在不同工况下的热流分配系数和温度变化;文献[8]发现热负荷作用对多片离合器摩擦片的摩擦因数和润滑油的黏度影响较大;文献[9]通过寻找润滑油温度与转速、油量等参数的关系,对最佳转速和油量进行了优化;文献[10]提出考虑摩擦热因素的多片离合器转矩计算模型,对传统计算模型进行了修正;文献[11]利用Abaqus建立湿式离合器有限元模型, 通过模拟Mises应力发现加压方式对摩擦副最大应力分布和应力轴向传递速度具有重要影响;文献[12]研究了离合器转速和液压油温度对离合器充油时间的影响规律,并制定了对转速和油温的控制策略;文献[13]通过Abaqus的数值模拟研究了卡簧约束对多片离合器接触应力温度场分布规律的影响,并通过实验验证了模拟结果的正确性。以上研究多集中于考虑多因素对多片离合器工作性能的影响,对离合器自身的优化考虑较少,多片离合器种类繁多,工作条件复杂,设计具有普遍适用性的多片离合器优化方案是一个亟待解决的问题。

本文针对电控限滑差速器中的多片离合器,通过建立热力学有限模型分析摩擦片和润滑油散热性能,在验证模型准确性的基础上进行多工况正交仿真,并以温度和热应力综合值最小为优化目标,通过后退法和遗传算法优化多片离合器结构参数,降低摩擦副表面温度和热应力值。

1 热传导和热流密度分配

多片离合器摩擦副之间的热传导属于对流换热过程,假设其为均质分布,则内部温度分布函数T=T(x,y,z)应满足拉普拉斯方程[14],即

(1)

配合如下一般边界条件:

(2)

其中:λ为与温度梯度有关的热传导系数;α为对流换热系数(与温度有关);T0为外界介质温度;Γ为摩擦副边界。

在各向同性、均匀连续介质中,通过某一截面的热流密度表达式为:

(3)

其中:q为热流密度;n为单位长度;T为材料温度;负号表示热量向温度低的方向传递。

多片离合器干摩擦接触过程中,认为摩擦产生的热量大部分被摩擦片和对偶钢片吸收,此时热流密度被分配到摩擦片和对偶钢片上,根据文献[15]的研究,分配比例与两者的材料属性相关,具体比例关系为:

(4)

其中:k为导热系数;ρ为材料密度;c为比热容;下标m表示摩擦片;下标d表示对偶钢片。

将摩擦副接触表面离散化,摩擦副接触示意图如图1所示。图1中,rn、rw分别表示摩擦片的内、外半径。

图1 摩擦副接触示意图

作用在微面积上的摩擦力可表示为:

dF=μpdA

(5)

其中：μ为摩擦系数;p为接触面压力;dA为微面积。在dt时间内,摩擦微表面所做的功全部转化为热量,即

dQ=μpr(x,y)ωrdAdt

(6)

其中:r(x,y)为(x,y)处的摩擦半径;ωr为旋转角速度。

电控限滑差速器多片离合器摩擦副在摩擦过程中产生的热流密度为:

(7)

结合(4)式、(7)式,摩擦片和对偶钢片的热流密度分别表示为:

(8)

2 热力学模型建立及验证

2.1 有限元模型

根据电控限滑差速器中的多片离合器实物,使用CATIA建立多片离合器主从动片三维数模,根据研究目的对三维模型进行如下简化[16]:① 具有外花键的传动轴对摩擦副的热力耦合影响不大,可以对外花键传动轴及其附件作忽略处理;② 摩擦副压盘不参与热传递,可忽略以减少工程计算时间;③ 摩擦副外壳限制摩擦片和对偶钢片的径向运动,并且传递对偶钢片的动力扭矩至传递钢链,其对摩擦副的热力耦合影响较小,可忽略此部件;④ 诸如回位弹簧、钢珠等零部件对传热影响较小,可忽略。

综上所述,含润滑油散热的有限元装配模型如图2所示。

图2 装配模型

表1 摩擦副材料属性

2.2 模型验证

电控限滑差速器通过控制左右侧多片离合器摩擦副的接合压力,实现对左右侧车轮的变转矩输出。常用车辆传动系统电控多片离合器的接合压力在0～1 MPa之间[10],选择0.4、0.6 MPa 2种压力工况作为热力学模型的模拟输入工况,摩擦副摩擦系数设置为0.15,摩擦片、对偶钢片相对转速为400 r/min[10]。摩擦副温度场如图3、图4所示。

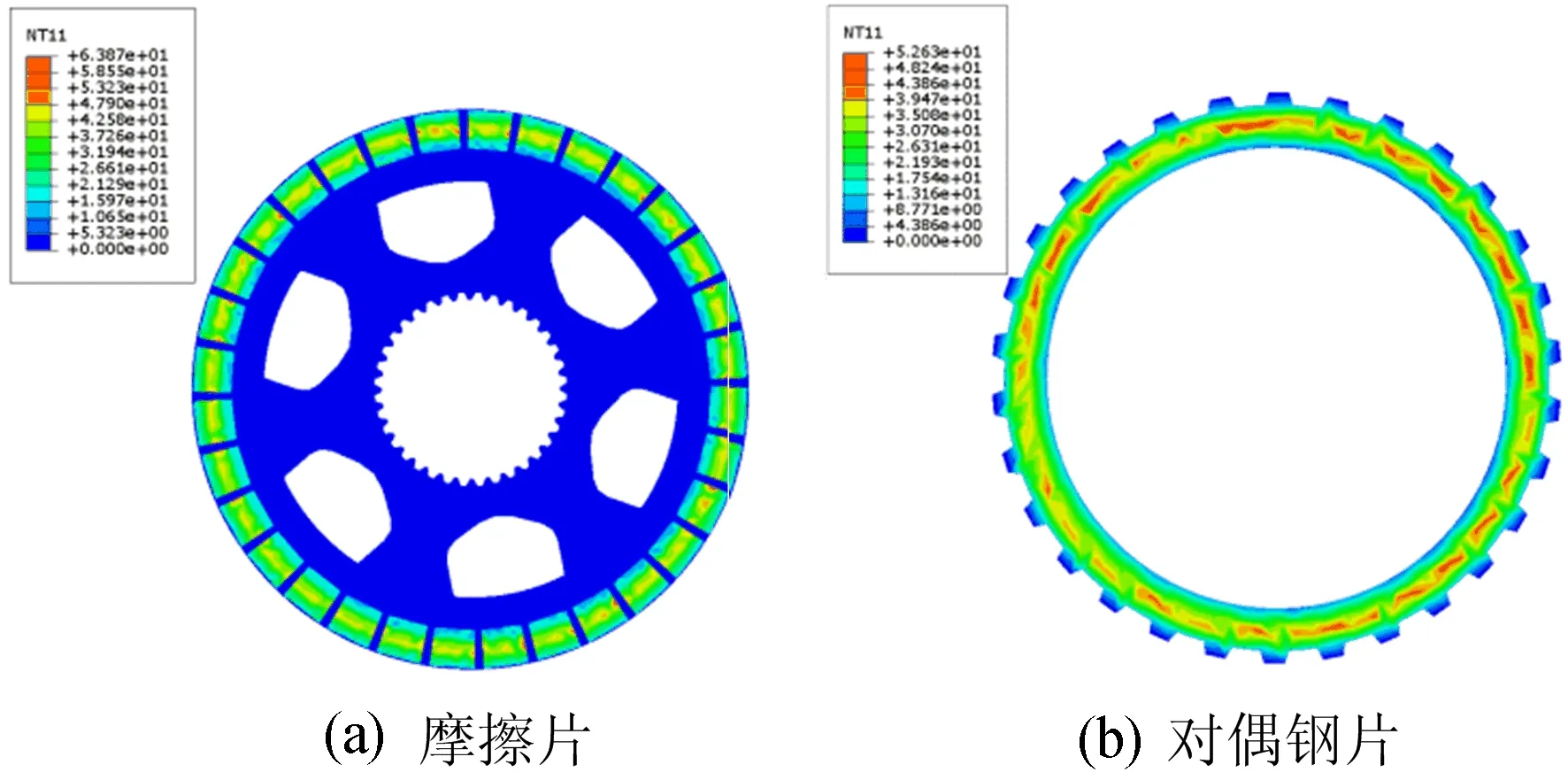
图3 压盘压强为0.4 MPa的温度场

图4 压盘压强为0.6 MPa的温度场

从图3、图4可以看出,摩擦衬片是摩擦片上的主要受热部件,带有内花键的旋转区域基本不传递热量,这与2.1节的简化是相符的。压强为0.6 MPa时摩擦片、对偶钢片表面的最高温度分别为97.47、79.33 ℃,0.4 MPa时对应的最高温度分别为63.87、52.63 ℃,随着压强的增加,摩擦副的平均温度和最高温度随之增大,同种工况下,摩擦片温度高于对偶钢片的温度,这也是摩擦片需采用特殊的耐热材料制作的原因。2种工况下的摩擦副温度场都存在热量在中心线处集中的现象,形成了环状的高温带,并且对偶钢片的温度集中现象比摩擦片更明显。根据热流密度分配方程,通过热力学模型计算出的多片离合器在润滑油流场中的散热结果如图5所示,由图5可知,0.4 MPa工况下的最高温度为49.10 ℃,位于自由液面处;0.6 MPa工况下的最高温为63.20 ℃,位于自由液面下方。随着压强的增大,壳体内部高温集中的现象变得明显,这是由于热流密度的增加,润滑油的流动不能对热量较高的部分进行快速扩散。

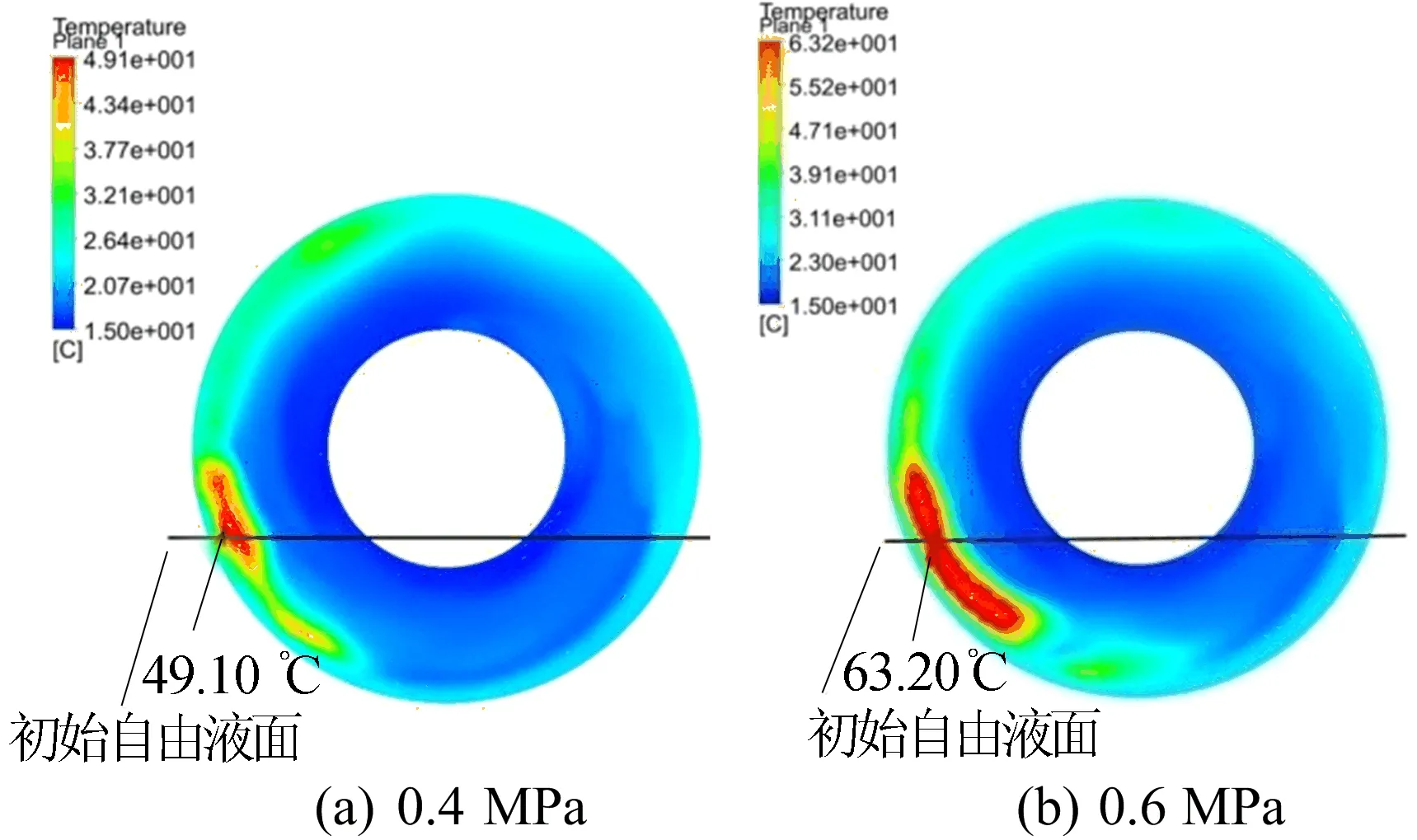
图5 不同压强温度分布

本文搭建的多片离合器试验台如图6所示,分别依据2种仿真工况进行台架试验,对摩擦副在限滑差速器壳体中的实际工作状态进行试验。为方便观察内部流场运动,差速器外壳采用透明PC材料按照与实际比例1∶1制作,使用热像仪获取摩擦副在壳体内部运动过程的温度场。

图6 多片离合器试验台

试验结果如图7所示。由图7可知，温度随压强变化的趋势与仿真结果一致,温度最高点均出现在初始自由液面附近。

图7 不同压强试验热像图

2种工况的仿真与台架试验数据对比见表2所列,相对误差均在10%以内,验证了本文搭建的热力学仿真模型的准确性、仿真方法的合理性。

表2 不同压强仿真与试验最高温度对比

3 多片离合器结构优化

3.1 设计变量的选取

合理的多片离合器结构尺寸可以提升动力传递特性,降低摩擦副表面温度和传动压力。应用二次响应曲面法确定优化设计目标函数,首先选取多片离合器摩擦衬片的数量、摩擦副厚度和摩擦副半径作为设计变量,通过改变相应的结构参数,利用热力学模型进行正交仿真。

海外投资保险制度是资本输出国政府对本国海外投资者在国外可能遇到的政治风险，提供保证或保险，投资者向本国海外投资保险机构申请保险后，在发生承保风险导致其受损失时，由该保险机构予以补偿的制度。其起源于美国的“马歇尔援助计划”，后经美国立法发展，成为国家法律制度，并被其他国家效仿。大多数发达国家建立和发展海外投资保险法律制度，使其成为保护海外投资的重要法律手段，具有鼓励私人海外投资的积极作用[7]。

(1) 改变摩擦衬片的数量。分别对32、28、24、16块摩擦衬片的多片离合器进行模拟,设置不变参数为摩擦片压盘压强0.8 MPa、摩擦系数0.15、相对转速400 r/min。16块摩擦衬片的仿真云图如图8所示。

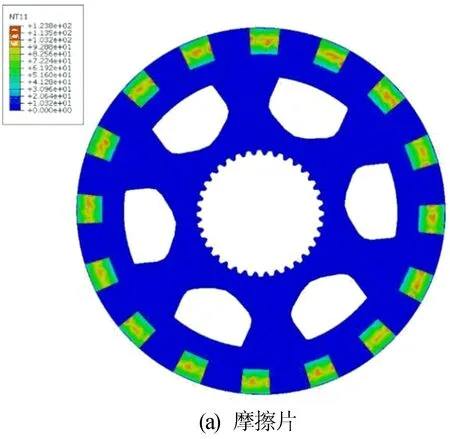
图8 16块摩擦衬片摩擦副温度场

摩擦副最高温度随摩擦衬片数量变化见表3所列。

表3 不同摩擦副数量下的温度

(2) 改变摩擦副厚度。分别对厚度为1.275(增加0.850 mm)、0.850(增加0.425 mm)、0.425(原始)、0.200 mm(减小0.225 mm)的多片离合器进行模拟。

设置不变参数为摩擦片压盘压强0.8 MPa、摩擦系数0.15、相对转速400 r/min。摩擦副最高温度随厚度变化见表4所列。

表4 不同厚度摩擦副最高温度

(3) 改变摩擦副半径。分别对摩擦衬片内外半径差11.23(增加2.00 mm)、13.23(增加4.00 mm)、15.23(增加6.00 mm)的多片离合器进行模拟。

设置不变参数为摩擦片压盘压强0.8 MPa、摩擦系数0.15、相对转速400 r/min。

摩擦副最高温度随半径变化见表5所列。

表5 不同半径摩擦副最高温度

选取以下设计变量:

X=(x1,x2,x3)=(η,t,w)

(9)

其中:η为摩擦片数量;t为厚度;w为摩擦片内径与外径的半径差。

设计如下的变量约束条件:

(10)

其中

x1∈[4,32];

x2∈[0.2,2];

x3∈[4.23,13.23]。

多片离合器在工作的过程中,既要考虑其承受高温的能力,又要考虑其承受热应力的作用,选定摩擦片温度T和应力M作为优化设计的目标函数,即

(11)

建立归一化后的目标函数关系为:

(12)

其中:Tmax=200 ℃为摩擦副允许的最高温度；Mmax=75 MPa为摩擦片许用应力；α、β为0.5，表示权重系数。

3.2 二次响应曲面设计

以3.1节的正交结果为原始数据,采用二次多项式对综合响应进行拟合。建立与摩擦片数量n、厚度t、摩擦片的内外半径差值w相关的回归模型，即

(13)

对试验结果进行显著性检验试验，验证结果的可靠性和模型的可信度、温度T(无量钢)的回归模型显著性，见表6所列。

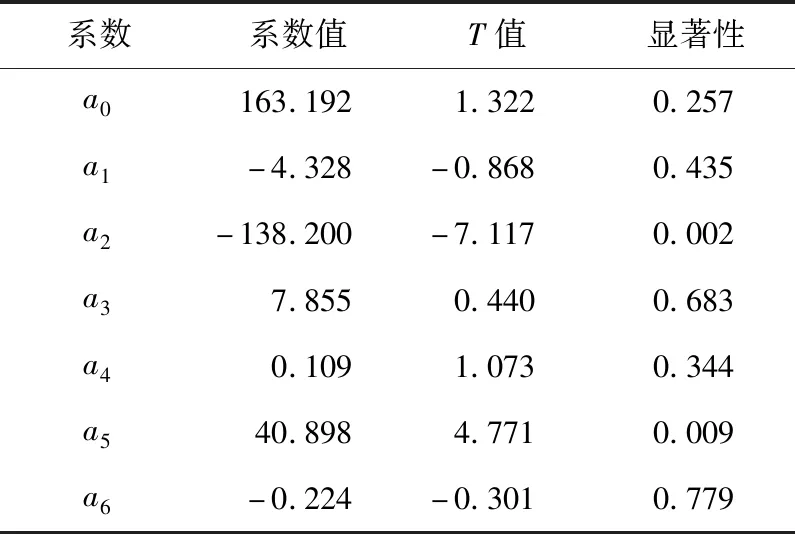
表6 温度回归模型拟合系数

从表6可以看出,除了系数a2、a5,其余系数的显著性检验均大于0.05,认为当前模型是不准确的,采用后退法重新建模,得到的优化分析结果见表7所列,优化后的系数a1、a6为0,且每一项系数的显著性都小于0.05,可以认为当前模型是准确的。

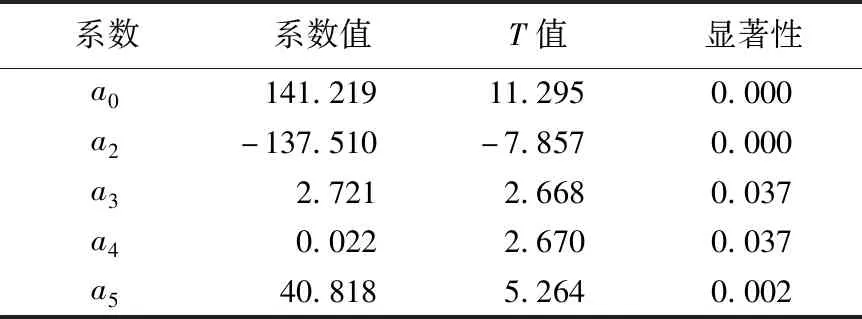
表7 优化后的拟合系数

同理,优化后的应力M(无量钢)的回归模型显著性见表8所列。

表8 应力回归模型拟合系数

设计优化方程为:

F(x)=0.002 5T+0.006 7M

(14)

3.3 优化结果

依据设计变量的范围和二次响应曲面回归方程,基于遗传算法进行优化设计,设置迭代次数为100、个体20位、变异0.3,优化迭代结果如图9所示。

图9 优化迭代

图9中:Mean fitness为每一代种群的平均适应度;Best fitness为每一代种群的最佳适应度。从图9可以看出,迭代到第20代以后,种群的平均适应度和最佳适应度开始趋于稳定。优化出的最优结果为n=32块、t=1.678 mm、w=7.408 mm，此时对应的温度、热应力分别为T=83.165 ℃、M=47.028 MPa。

4 结 论

(1) 本文建立了多片离合器热力学模型,开展了2种不同压强下温度场的仿真分析,并通过所搭建的多片离合器试验台架,对2种工况的实际工作状态进行测试,试验结果验证了所建模型的准确性和仿真方法的合理性。

(2) 基于建立的热力学模型,分别对不同接触面积、不同厚度、不同半径下的摩擦副温度场进行仿真分析,得到了摩擦副结构参数的改变对其热力学特性的影响规律,摩擦片温度随着半径和摩擦衬片块数的增加而增大,随着摩擦片厚度的增加而减小。

(3) 针对多片式离合器的传动特性,采用二次响应曲面法确定优化设计目标函数,建立关于摩擦片参数的回归模型,并采用遗传算法对目标函数进行优化,得到了最优参数。