基于单自由度Watt机构的拟人步态下肢康复机器人设计

赵 萍, 宋 词, 鲍紫怡, 宋皖兵, 康 甜, 黄 德

(合肥工业大学 机械工程学院,安徽 合肥 230009)

截至2019年,我国65岁以上老年人占比为12.63%,此比例将持续上涨且长期维持在高位[1]。人口老龄化会使得机能衰退导致的下肢灵活性下降群体以及脑卒中、脑损伤等疾病导致的偏瘫患者越来越多[2],他们迫切需要进行下肢康复训练来恢复健康。传统的人工康复训练效果受环境、医师专业水平等影响,且操作标准与评定指标也无法规范统一;而下肢康复机器人由于稳定性好、重复性强,能通过高强度重复性运动与精准控制力实现辅助治疗功能,近年来具有很高的研究热度[3]。

按训练姿态,下肢康复机器人主要分为坐卧式和立式。相比于坐卧式,立式与人体下肢的运动模式更为相符,康复效果尤为明显[4]。国内外立式下肢康复机器人如瑞士Hocoma公司的Lokomat[5]、德国柏林自由大学的Haptic Walker[6]及上海交通大学的下肢康复外骨骼机器人[7]等,均能通过多个电机协作带动下肢按正常步态模式运动,实现步行康复训练,但它们因自由度较多存在结构复杂、控制不便、造价昂贵等问题,难以大范围推广。因此设计一款结构简单的单自由度下肢康复机器人成为一项新任务。文献[8]、文献[9]分别设计出基于四杆机构、Jansen八杆机构的单自由度下肢康复机器人,但它们的步态轨迹复现精度较低;文献[10]设计出基于凸轮连杆机构的单自由度下肢康复机器人,其步态轨迹复现精度较高,但凸轮的设计加工较复杂。

执行机构是单自由度下肢康复机器人的核心,对其进行优化设计也成为研究重点。文献[11] 基于全局优化的Powell算法,对一种串联组合式单自由度机构进行了轨迹综合;文献[12]基于运动映射对单自由度凸轮连杆机构进行刚体导引,得到具有最优运动模式的下肢康复机构;文献[13]结合代数方法与优化技术对Stephenson-Ⅲ型六杆机构进行轨迹综合,较好地生成指定步态轨迹。

针对下肢康复机器人控制复杂、造价昂贵的问题,本文以正常步态轨迹为目标轨迹,对单自由度Watt-Ⅰ型六杆机构进行轨迹综合,得到机构尺寸;利用ANSYS软件进行机构的拓扑优化和响应面尺寸优化,实现轻量化设计;最后,基于优化后的六杆机构设计出一款单自由度拟人步态下肢康复机器人。本文创新点在于执行机构具有单自由度,仅需一个匀速电机即可驱动机构复现正常步态轨迹,具有结构简单、操作方便、经济实用等特点。

1 下肢康复机构尺寸优化设计

1.1 机构选型及其运动学模型

常见平面连杆机构中四杆机构结构简单,无法较准确地拟合出人体踝关节轨迹曲线,而六杆机构可以生成更为复杂的轨迹曲线,故选择平面六杆机构。单自由度平面六杆机构有Watt-Ⅰ 、 Watt-Ⅱ 、 Stephenson-Ⅰ 、Stephenson-Ⅱ、Stephenson-Ⅲ等类型,其中Watt-Ⅰ型六杆机构具有运动链较为简单、结构紧凑的优点,因此选其作为下肢康复机器人执行机构。

Watt-Ⅰ型六杆机构如图1所示。在定坐标系xoy中,设xJ、yJ为任一铰链中心J的坐标;x1～x11为各构件长度;r1、r2分别为A与O1、C与D的距离;θ0为x轴与OO1的夹角;θ1为曲柄OA的转角;θ2为OO1与AB的夹角;θ3为OO1方向与O1B的夹角;α1、α2分别为△ABD的其中2个内角;β1、β2、β3分别为△BO1C的3个内角;φ1=∠OO1A,φ2=∠BCD,η=∠EDF。

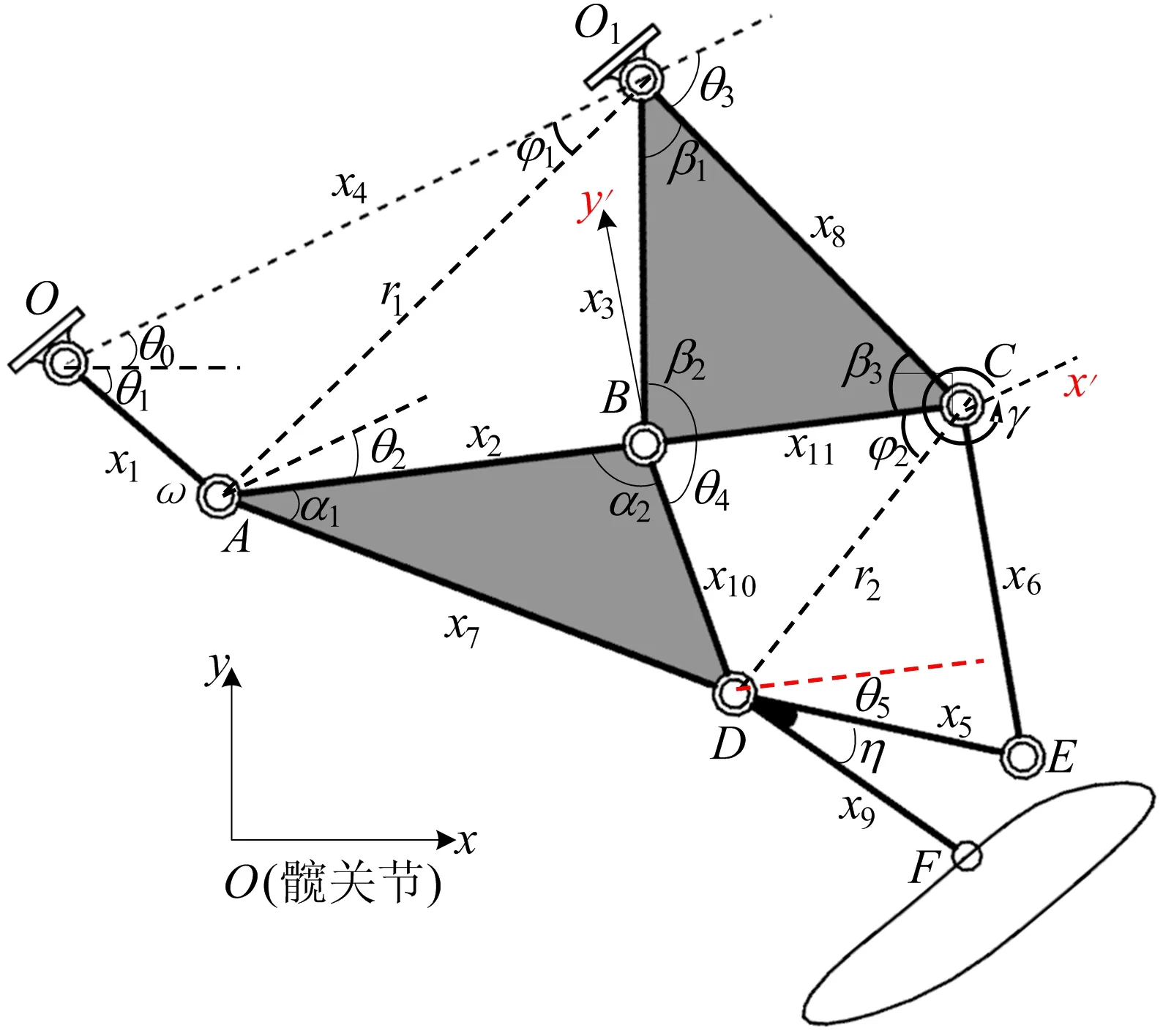
图1 Watt-Ⅰ型六杆机构

若OABO1可以看成四杆机构,则有如下关系式[14]:

(1)

其中

M=x4-x1cosθ1;

N=-x1sinθ1;

可以推导出:

xB=xA+x2cos (θ0-θ2),

yB=yA+x2sin (θ0-θ2)

(2)

xA=xO+x1cos (θ0-θ1),

yA=yO+x1sin (θ0-θ1)

(3)

(4)

(5)

以B为原点,BC为x′轴建立动坐标系x′By′,设∠CBD=θ4,则有:

θ4=2π-α2-β2-(θ3-θ2)

(6)

设OO1与x′的夹角为γ,则有:

γ=β1+β3-θ3

(7)

BDEC可看成另一个四杆机构[15],设x′轴与DE的夹角为θ5,类比四杆机构OABO1可得:

(8)

其中

设六杆机构的末端F点在动坐标系x′By′中的坐标为(xF′,yF′),则有:

xF′=x10cosθ4+x9cos (θ5+η),

yF′=-x10sinθ4-x9sin (θ5+η)

(9)

根据齐次坐标变换公式,可得机构末端F点在定坐标系xoy中的坐标为:

xF=xF′cos (γ+θ0)-yF′sin (γ+θ0)+xB,

yF=xF′sin (γ+θ0)+yF′cos (γ+θ0)+yB

(10)

1.2 目标函数与约束条件

1.2.1 目标函数

设计变量为x=[x1x2x3x4x5x6xOyOθ0α1x7β1x8x9ηθinitial]T,其中θinitial为目标轨迹起点对应的曲柄转角。本团队使用人体运动捕捉设备提取了34名身高介于1.62～1.85 m的健康人正常行走时的下肢运动轨迹,并将它们回归成运动棒图,如图2所示。以其中的踝关节轨迹为目标轨迹,其上任意相邻2个轨迹点的时间差相等。

图2 人正常步行时的下肢运动棒图

根据目标轨迹点的数目m将曲柄的一周转角等分,自起点开始依次得到各轨迹点对应的曲柄转角,由(1)～(10)式可以求得它们对应的机构末端F点的坐标(xFj,yFj)(j=1,2,…,m),为使机构末端生成的点与对应目标点的平均误差最小,建立目标函数为:

(11)

其中,(xGj,yGj)为(xFj,yFj)对应的目标轨迹点坐标。

1.2.2 约束条件

考虑实际情况,杆长应为正值,因此有杆长非负条件式如下:

x1,x5,x6,x7,x8,x9,x10,x11>0

(12)

为确保机构具备良好的运动学特性,应满足曲柄存在条件,即最短杆与最长杆长度之和小于等于其他两杆长度和。令x1为最短杆,铰链O即为周转副,则有:

x1-x2-x3+x4≤0,

x1+x2-x3-x4≤0,

x1-x2+x3-x4≤0

(13)

为保证机构传力性能,应使最小传动角的值不低于40°,可得传动角约束条件式为:

(14)

为使杆DE、CE能够正常运动,应保证在1个运动周期中杆DE、CE、CD始终能构成一个三角型,则有装配条件式为:

maxr2-x5-x6≤0,

|x5-x6|-minr2≤0

(15)

1.3 尺寸综合

本文先用基于全局优化的遗传算法优化目标函数,再将其结果作为初始点,继续用基于局部优化的拟牛顿算法迭代寻优,进一步获得更好的结果,算法流程如图3所示,最终得到优化后的机构如图4所示。

图3 算法流程

图4 优化后的机构简图

目标步态轨迹和机构F点轨迹的对比情况如图5所示。目标轨迹点与对应的机构轨迹点之间的平均位置误差仅为7.76 mm,它们的形状与时序基本一致,该机构能很好地复现正常步态轨迹。

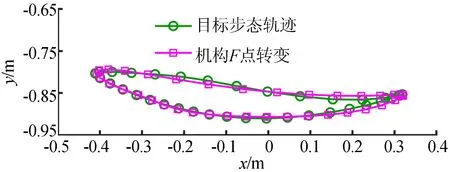
图5 机构F点轨迹与目标步态轨迹对比

2 下肢康复机构轻量化设计

轻量化设计旨在满足一定的寿命和可靠性要求的前提下,实现结构自重的最小化,可以起到节省材料、节约能源的作用。

本节将对六杆机构进行轻量化设计:对六杆机构进行静力学分析,检验机构强度与刚度是否满足设计要求,并求出最危险工况;在最危险工况的情况下进行六杆机构的结构优化设计;针对六杆机构不同的优化设计阶段,选用不同优化方案;在设计初期,为获得基本概念模型,采用拓扑优化;在详细设计阶段,为获得机构具体尺寸,采用结构的尺寸优化。

2.1 静力学分析

在运动周期的不同时刻,各杆件的相对位置不同,受力情况也不相同。因为曲柄转速较慢,惯性力影响可以忽略,所以使用ANSYS Workbench中static structure模块分析六杆机构受力情况。分别取曲柄与机架夹角为0°、45°、90°、135°、180°、225°、270°、315°时的8种工况进行求解[16],通过比较应力极值和最大位移得出8种工况中最危险工况,近似等于整个运动过程中的最危险工况,并验证机构设计的合理性。

在SolidWorks环境下分别构建8种工况的三维简化模型,并分别导入ANSYS Workbench中进行有限元分析,基本操作步骤如下:

(1) 设置材料参数。选用45钢,材料弹性模量E=210 GPa,泊松比μ=0.269,屈服强度为355 MPa。

(2) 施加载荷。根据GB 24436—2009规定,承载人体部分重量的装置应能承载750 N±15 N,因此在单侧脚踏板面上施加375 N载荷。

(3) 施加位移约束条件。机架杆外侧面设置固定约束;在机构运动过程中,曲柄转速较慢,可以认为曲柄轴不发生转动以及轴向移动,因此在曲柄的端面设置为固定约束。

(4) 接触类型设置。各铰链处的接触类型设置为Frictional,摩擦系数设置为0.15;连杆与足部踏板之间、曲柄与曲柄轴之间均设置为绑定接触。

仿真输出结果为等效应力与总变形,计算结果见表1所列。

表1 不同工况下六杆机构静力学仿真数据

由表1可知,在曲柄与机架夹角为90°时,机构的应力达到最大值289 MPa,小于材料45钢的屈服强度355 MPa,安全系数为1.23;在曲柄与机架夹角为135°时,六杆机构出现最大变形量,其值为0.002 321 m,根据GB 24436—2009规定,变形量不得超过1%,满足设计要求。综上可知,8种工况中应力极值与最大变形量均分别满足强度与刚度要求,因此六杆机构能够正常运行,不会发生破坏。

2.2 拓扑优化

拓扑优化是一种以材料为优化对象,在模型原设计空间中寻找最佳分布方案的优化方法。装配体零部件上会存在多余重量,造成材料浪费,运动部件需承受更高载荷,而通过拓扑优化能得到零部件最佳形状,可以有效降低成本,提高能源利用效率。

拓扑优化设计区域设置为构件ABD和构件BO1C。在设计初期,只能粗略设计构件ABD和构件BO1C的结构形式,导致构件体积较大,存在较多多余重量;在拓扑优化阶段,通过ANSYS Workbench软件中shape Optimization工具,确定2个构件合理的结构外观。由静力学仿真结果可知,构件OA、构件CE、构件EDF的应力值较大,多余重量较少,因此不对这些部分进行拓扑优化。

确定构件ABD与构件BO1C的危险工况。由表1可知,最大位移数值较小,因此仅以应力极值为依据确定最危险工况。由实验数据可知：在曲柄与机架夹角为180°时,构件ABD达到极值233 MPa；在曲柄与机架夹角为225 °时,构件BO1C达到极值102 MPa。由于构件ABD应力值较大,且接近材料屈服强度,而构件BO1C应力值较小,取曲柄与机架夹角为180 °时的情况为最危险工况,进行拓扑优化。

目标函数为整体质量,目标质量分数为50%,得到优化结果,并据此在Solidworks中修改原有三维模型,得到最终简化模型,如图6所示。

图6 拓扑优化后处理结果

2.3 响应面优化

响应面优化为尺寸优化的一种方法。本节通过响应面优化对构件ABD与BO1C的尺寸参数做进一步优化。

定义响应面优化的设计变量、目标变量和状态变量。设计变量示意图如图7所示。6个设计变量分别为:构件ABD中,左截面至左侧铰链中心点的距离p3,右截面至右侧铰链中心点的距离p4,板厚度p5;构件BO1C中,上截面至构件BO1C边缘的距离p6,左截面至构件BO1C边缘的距离p7,板厚度p8。目标变量为质量p1,状态变量为最大等效应力p2。

图7 设计变量p3、p4、p6、p7示意图

为得到较为精确的响应面模型,通过自定义的方法生成均布样本空间的40个实验设计点,并得到上述样本点响应值,根据样本数据在response surface中完成响应面模型的构建。计算所得2个目标参数响应面模型拟合精度分别为0.999 99和0.997 84,满足精度要求,可进一步用于优化设计。采用screening算法进行优化求解,最终得到6个设计变量对于目标参数p1、p2的优化结果。

响应面优化的最终结果见表2所列。

表2 六杆机构设计变量的优化结果

优化前模型总质量为62.61 kg,优化后模型质量为42.16 kg,质量减少达到32.66%,且机构应力极值为259.390 MPa,安全系数为1.37,满足材料强度要求。

3 下肢康复机器人结构模型

下肢康复机器人结构示意图如图8所示。

1.滑轮 2.减重块 3.安全背心 4.链传动机构 5.电机 6.踏板 7.扶手 8.六杆机构 9.机架 10.钢丝绳

图8立式下肢康复机器人主要由机架、步态模拟机构、减重系统、传动系统组成。机架用于连接各个部分并包含扶手,根据《GB/T 10000—1988中国成年人人体尺寸》,设定扶手可在1.20、1.13、1.06 m 3个高度调节。步态模拟机构为布置在两侧的一对单自由度六杆机构,它们的末端固连踏板。

康复训练前期,由于患者下肢力量匮乏,应启用悬吊式减重系统。减重系统由安全背心、钢丝绳、滑轮和减重块组成,钢丝绳通过滑轮一端连接安全背心,另一端连接减重块,可根据实际需求通过增、减减重块数目调整减重量。传动系统选用链传动机构,以实现紧凑可靠的远距离传动。

康复训练时,患者的双脚固定在踏板上,被两侧始终保持180°相位差的步态模拟机构牵引,使踝关节沿近似的正常步态轨迹运动,进而让大、小腿按照步行规律重复摆动,实现模拟行走动作。考虑到不同康复训练阶段需要不同的训练速度,选用带有调速器的减速电机。

该下肢康复机器人只需1个匀速电机驱动即可近似复现正常步态轨迹,相较于其他大多数下肢康复机器人,结构更加简单，使用更加方便，具有普惠性。

4 结 论

(1) 本文提出并设计了一种基于Watt-Ⅰ型六杆机构的单自由度下肢康复机构,该机构目标轨迹点与对应的机构轨迹点之间的平均位置误差仅为7.76 mm,能很好地复现正常步态轨迹。

(2) 基于拓扑优化和响应面优化方法对六杆机构进行了轻量化设计,在保证材料强度足够的前提下使其质量减少了32.66%。

(3) 基于优化后的六杆机构设计了一款单自由度拟人步态下肢康复机器人,该机器人仅需1个匀速驱动即可复现正常步态轨迹,实现步行康复训练,具有结构简单、使用方便、经济实用的优点,适合向大众推广。