基于优化模型的停车场车位规划实验设计研究 *

巩 斌,李 斐,朱家明

(安徽财经大学)

0 引言

目前，中国汽车人均保有量持续的在增长，这给人们的工作生活、出行等带来极大的方便和快捷，但停车难的问题却变得越来越突出，因此，停车场的规划变得更加重要.解决这一问题，当然可以通过增加停车场数量加以解决，但在土地有限的情况下，对现有停车场车位进行优化布局是个明智之举[1].即对停车场的周边空间环境、停车场车位的排列布局，车场内车辆通道畅通性、停车的难易与否等因素加以考虑进行优化，尽可能地增加停车场的数量，这将大大增加停车位的利用率、释放停车压力具有重要的现实意义.

停车是否便利、高效一直与居民的生活息息相关，也是当地政府现代治理能力的一种具体体现.同时，停车位的优化问题，中外学者对此研究也方兴未艾.对于一个已知的停车场进行车位规划时，即使不考虑其外围环境因素，也必须要考虑停车场本身的形状、大小等直接因素，还有车位的大小与形状.对于此静态的最优化问题，该文通过构建非线性整数规划模型，考虑消防因素条件下，实证分析某商场停车位优化这一实际案例，求解出最优停车位规划设计[2].

1 优化实验设计

1.1 设计假设

为了使建立的模型通用和便于理解，首先假定一个指定车辆出入方向的停车场，其长79 m，宽26.5 m，并对其进行优化以使车位数尽可能的多.在当前寸土寸金的城市中，试着分析垂直式，平行式和斜列式不同车位排列的模式，在满足车道足够车辆正常行驶与停车的情况下，让车位进行合理化排放，实现停车位数量最大化.因此，针对车辆的三种排放方式：垂直式，平行式和斜列式分别进行分析，对转弯角度进行精准计算，得出每种情况对应的不同最优角度值，充分利用三种排放方式进行排列组合，使停车场的空间利用率达到最高[3].分析的停车场地形图如图1所示.

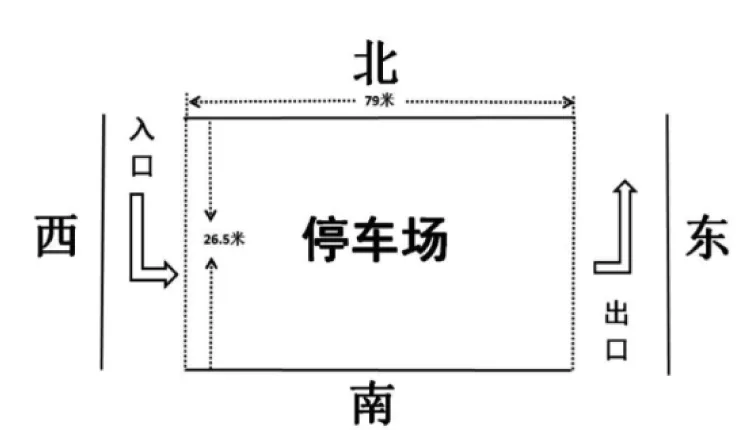
图 1 停车场地形图

1.2 车位排列方式

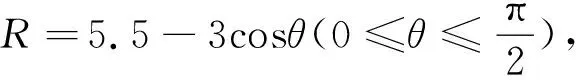
表1 公式字母符号及其代表的含义

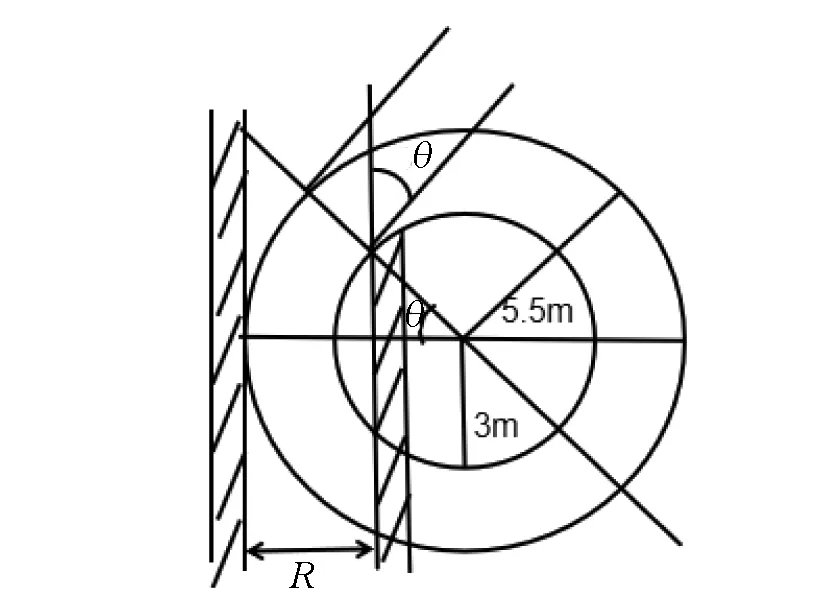
图 2 车辆转弯示意图

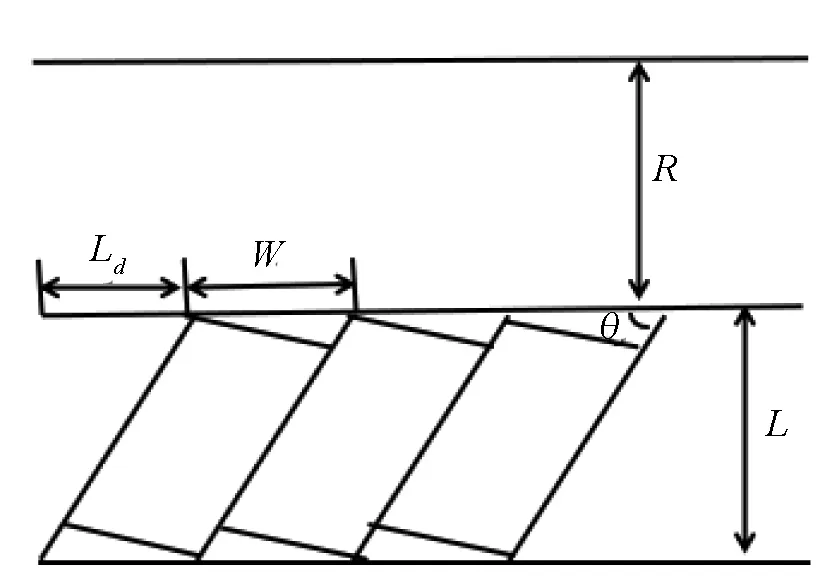
图3 停车位与通道设计

1.2.1 平行式排放

当车辆平行停放时，夹角θ为0，通道宽度R=5.5-3cosθ=2.5 m，车辆占据了长2.5 m(L表示，下同)、宽5.5 m(W)的长方形位置，停车场宽：B=R+L=5 m，停车位个数为X=A/W=A/5.5 (A为停车场长度)，如图4所示.

图4 车辆平行式排放示意图

1.2.2 垂直式排放

如图5所示，当车位垂直于通道时，则夹角为直角，R=5.5-3cosθ=5.5 m，L=5.5sinθ+2.5cosθ,W=2.5 m，B=R+L=11 m，X=A/W=A/2.5.

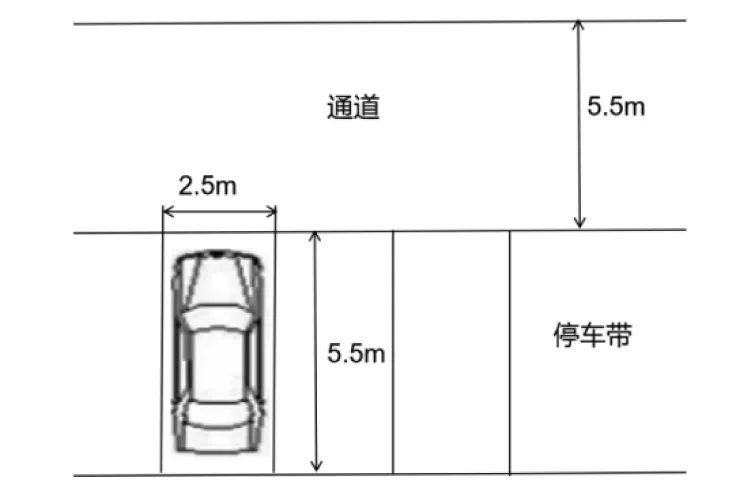
图 5 车辆垂直式排放示意图

1.2.3 斜列式排放

如图6所示车辆斜放时，车辆和通道之间夹角为0≤θ≤π/2，通道宽度R=5.5-3cosθ，车位长度L=5.5sinθ+2.5cosθ，车位宽度W=2.5/sinθ，停车场宽B=R+L=5.5-0.5cosθ+5.5sinθ，停车位末端距离Ld=5.5cosθ+2.5cosθ/tanθ，停车位个数X=(A-Ld)/W.

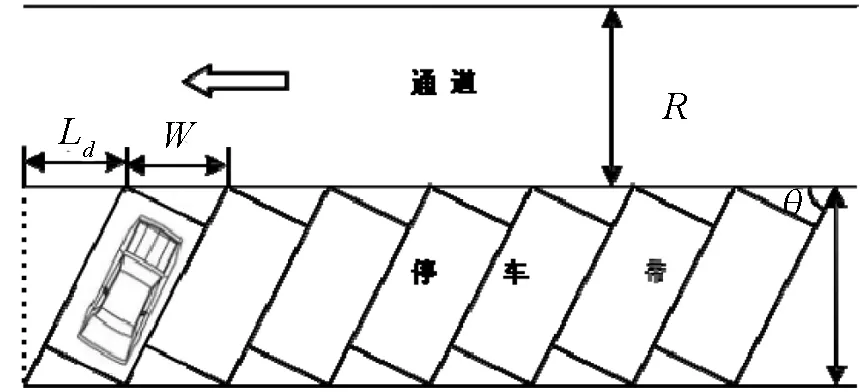
图6 车辆斜列式排放示意图

1.3 车位停放不同模式下的模型构建

停车场停车位有以下两种情况，其公式中字母符号及其所代表的含义见表1，而且还约定位于同一区的汽车停放角度一样.

1.3.1 停车场周围不包含垂直，平行排放车位时，即整个停车场采用斜列式排放

a.当m=2n时，停车带在每个通道两边都设置[4]，令C=6 m，规划模型a1为：

st.nR+mL=n(5.5-3cosθ)+m(5.5sinθ+2.5cosθ)=26.5

Xi=2(A-Ld-2C)/W=2(79-5.5cosθ+2.5cosθ/tanθ-12)/(2.5/sinθ)

m=2n,

m,n∈Z*

b.当m=2n-1时，即前n-1个通道两侧无停车带，只在第n个一侧有，规划模型b1为：

st.(n-1)R1+R2+(m-1)L1+L2=

(n-1)(5.5-3cosθ1)+(5.5-3cosθ2)+(m-1)(5.5sinθ1+2.5cosθ1)+(5.5sinθ2+2.5cosθ2)=26.5

Xi=2(A-Ld1-2C)/W1=2(79-5.5sinθ1+2.5cosθ1-12)/(2.5/sinθ1)

Xn=2(A-Ld2-2C)/W2=2(79-5.5sinθ2+2.5cosθ2-12)/(2.5/sinθ2)

m=2n-1,

m,n∈Z*

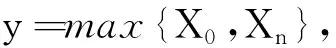
1.3.2 停车场周围包含平行，垂直排放车位，即停车场周围一圈的车位为垂直或平行方式，中间采用斜列式排放[5]

a.当m=2n时，规划模型a2为：

st.nR+mL=n(5.5-3cosθ)+m(5.5sinθ+2.5cosθ)=16.5

Xi=2(A-Ld-2C)/W=2(57-5.5cosθ+2.5)/(2.5/sinθ)

m=2n,

m,n∈Z*

b.当m=2n-1时，规划模型b2为：

st.(n-1)R1+R2+(m-1)L1+L2=

(n-1)(5.5-3cosθ1)+(5.5-3cosθ2)+(m-1)(5.5sinθ1+2.5cosθ1)+(5.5sinθ2+2.5cosθ2)=16.5

Xi=2(A-Ld1-2C)/W1=2(57-5.5sinθ1+2.5cosθ1)/(2.5/sinθ1)

Xn=2(A-Ld2-2C)/W2=2(57-5.5sinθ2+2.5cosθ2)/(2.5/sinθ2)

m=2n-1,

m,n∈Z*

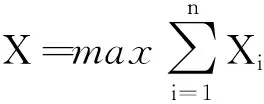
2 消防因素下商场停车场的优化实际案例

2.1 设计方案

为了提高消防规划的可操作性，考虑火灾带来的商场及停车场重大灾害，对停车场进一步优化设计，既要停车位尽量多、车位方向和分布更方便停车；又要设计出消防通道，并且应保持其畅通.图7是一大型商场停车场平面分布图(参数如图中所标示).在停车场的左侧和下侧最外围以水平方式排列车辆，沿着商场外围三侧也以水平方式排列，同时停车场的三面中间路面均设立6 m宽的消防路线，左侧右侧和下侧停车场在消防路线的外围均以斜列式排列车辆，在停车场的三角区域也按斜列式排列方式排列车辆，以达到最高利用率[7].

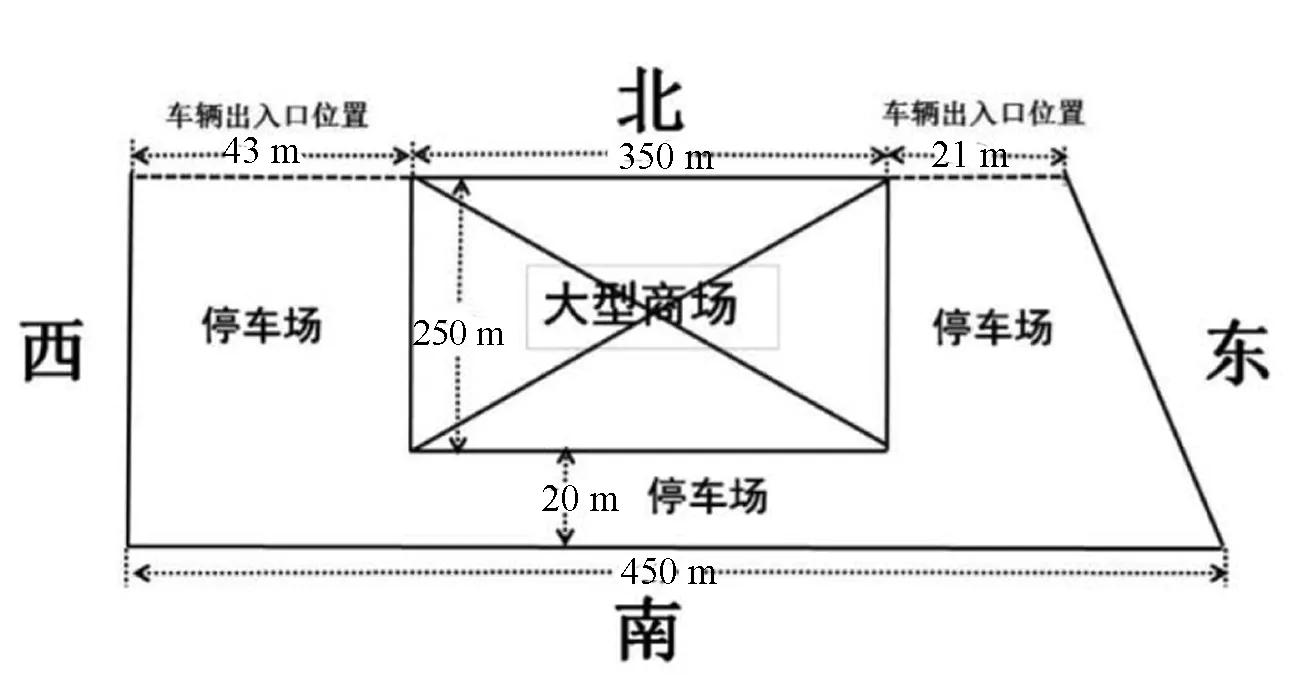
图7 商场停车场地形图

2.2 优化模型求解

2.2.1 优化模型具化形式

max=(250-Ld)/W

2R+5L=29.5

R=5.5-3cosθ

L=5.5sinθ+2.5cosθ

W=2.5/sinθ

Ld=5.5cosθ+2.5cosθ/tanθ

则停车场下方中心斜列式排列时，其最优化模型具化形式a22为[9]:

max=(420-Ld)/W

R+L=6

若为深部地热上涌与临近断层活动引起的，那么井水温度应该为渐变型上升，与本次异常情况不符，因此排除此种可能性。

R=5.5-3cosθ

L=5.5sinθ+2.5cosθ

W=2.5/sinθ

Ld=5.5cosθ+2.5cosθ/tanθ

2.2.2 模型求解结果

在停车场的左边和下边分别按水平方式排列车辆求解得出总共可以排放129辆车辆，沿着商场的外围也以平行方式排列车辆，求解得出总共可以排放153辆车辆.模型a21在商场的左侧停车场的中间部分，设立6 m宽的路作为消防通道，消防通道周围以斜列式排放车辆，模型a21求解见表2[10].

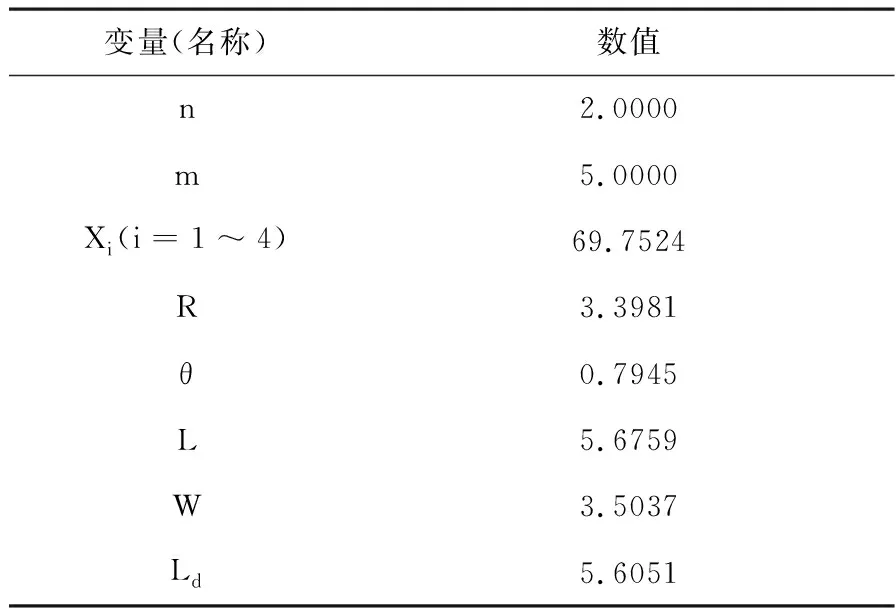
表2 模型a21求解输出表

由模型解得出，停车场左侧斜列式排列区域可以排列345辆车辆，加上拐角处8辆，总共可以排列353辆车辆.

停车场下方中心斜列式排放模型a22求解见表3.

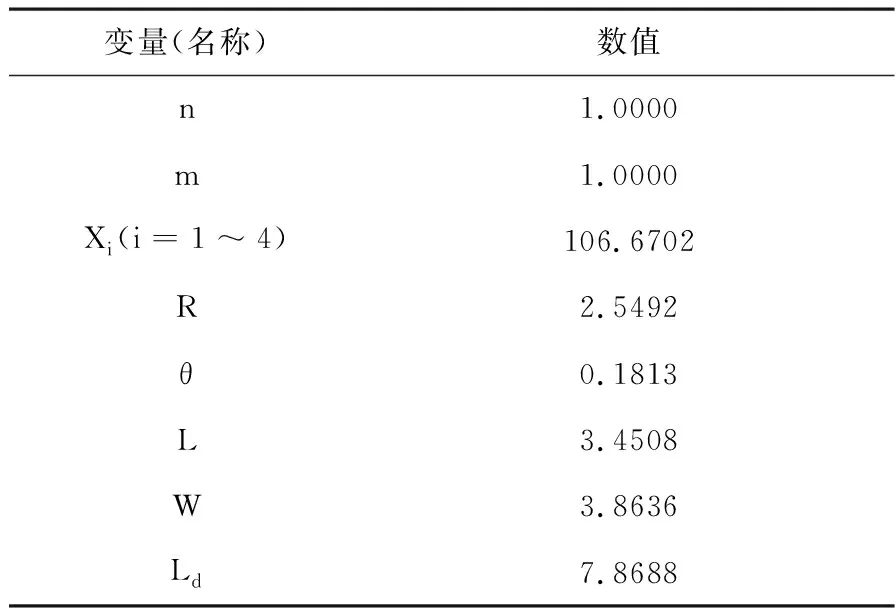
表3 模型a22求解输出表

由模型解得出，停车场下侧斜列式排列区域可以排列106辆车辆.在停车场的右侧区域，斜列式排列方式按照模型a22得出的结果进行排列，其右侧矩形区域智能排列一列斜列式，在三角形区域可以排列5列斜列式.运用三角函数求解，得出总共可以排列245辆.

综上，商场停车场最大停车数量为129+153+353+106+245=986辆，停车场平面设计图如图8所示.

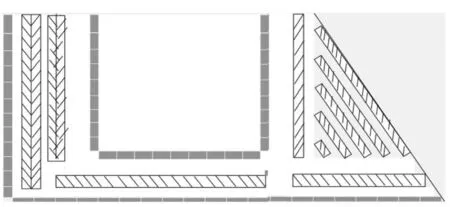
图8 商场停车场平面设计图

2.3 模型的验证

给定出入口的停车场车位设计的函数关系模型中，计算总函数关系式：

Xi=2(79-5.5cosθ+2.5cosθ/tanθ-2C)/(2.5/sinθ)

其中

B=2(5.5-3cosθ)+4(5.5sinθ+

2.5cosθ)

为了计算简便，直接设定停车带两端的纵向通道宽度C为6 m[11].但实际上，B和C值因停车场周边环境不同会有误差.因此对B和C取不同值时，进行灵敏度分析，用MATLAB运行结果见表4.

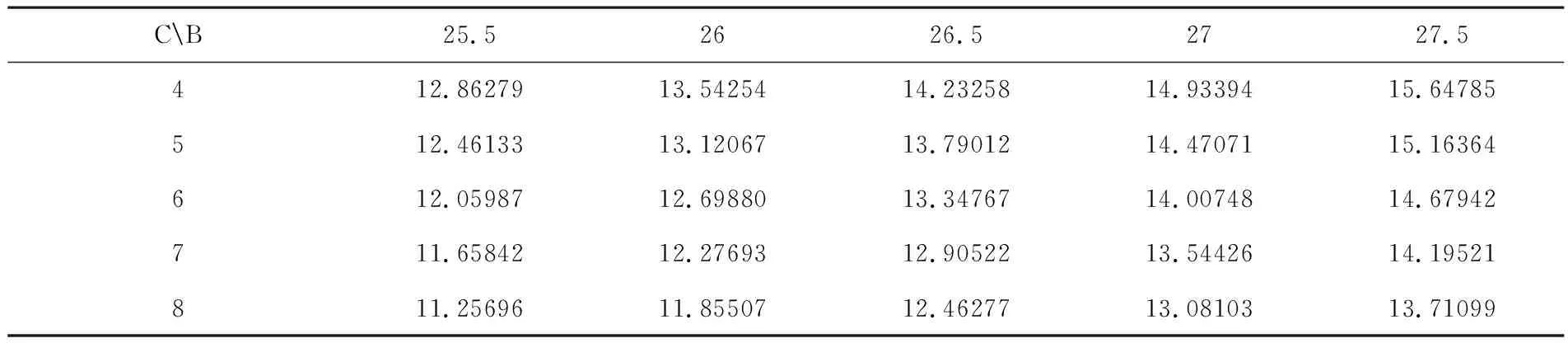
表4 不同B和C值下对于Xi的值

根据表4中的数据作图，可得Xi对B和C的灵敏度分析图，如图9所示.由灵敏度分析可知，当C一定时，Xi值随着停车场宽度B的增大而增大，且增大值量慢慢增大；当C值不同时，停车带两端的纵向通道宽度C在4～5 m之间时增长较快，6～8 m之间，增长较慢.这与实际情况相吻合.

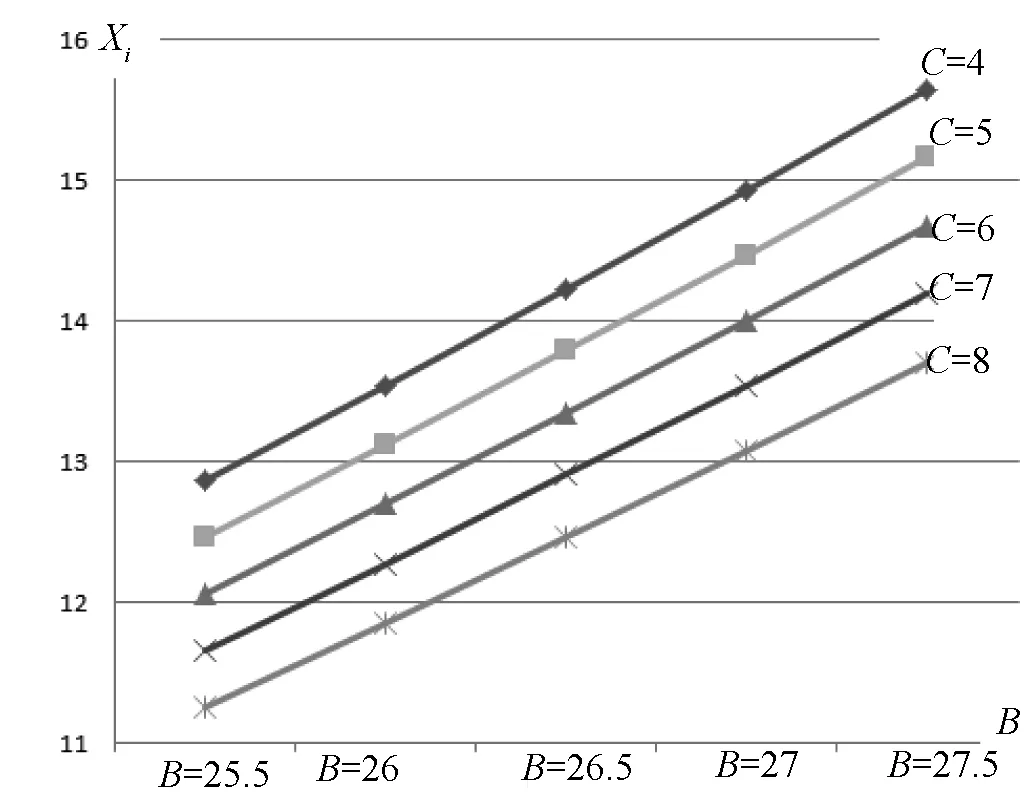
图9 xi对B和C的灵敏度分析图

3 结论及建议

(1)停车场车位优化模型不仅适用于停车场车位的最优设计，还适用于其他整数规划问题；在当前中国各大城市停车位供不应求的背景下，停车场的优化设计与改造势在必行，该模型有着很强的应用性和推广空间.

(2)随着停车场的发展，停车场已成为建筑的一个门户.如果情况许可，不仅对停车场进行车位优化，而且还要对场内进行交通流向诱导标识、交通安全设施设计；还可以根据实际情况规划出MPV车位、房车车位、校车车位等，方便不同的车辆使用，提升人们使用停车场安全便捷、服务周到的心理体验.

(3)随着大量汽车进入千家万户，对现有存量停车场车位的优化规划，进而解决停车难的问题是远远不够的；还必须新建增量停车位，其规划要超前，供给要加大.提高现有停车位的管理效率以及增加新停车位的供给，不能单纯的依靠收费进行调节；更不是赶时髦简单地开发一个“城市通”APP小程序进行收费就万事大吉了[12].这涉及到当地政府各相关职能部门的管理能力、地方立法支持、经济手段的运用和调节、管理成本的控制以及城市交通“智慧大脑”的建设，需要综合提升地方政府现代治理能力建设.