电主轴参数化及结合响应面法的多目标优化

王洪申，连亚东，黄忠金

（兰州理工大学 机电工程学院，兰州 730050）

精密高速数控机床在机械、航空航天、电气、军工、自动化等行业发挥着广泛的作用。电主轴是数控机床领域出现的将机床主轴与主轴电动机融为一体的新技术产品，电主轴的性能很大程度上决定了数控机床的性能。为了提高电主轴的性能指标，有必要对电主轴的结构和性能进行仿真和优化研究[1]。

目前，针对电主轴的仿真优化国内外一些专家学者都做了相应的研究，郭维祺等[2]以稳定性裕度为优化目标，将电主轴轴向尺寸作为设计变量，采用高效微型遗传算法实现高速静压内置式电主轴系统的稳定性优化。闫如忠等[3]运用模态理论和响应面法分析了高速磨削电主轴的预应力模态特性和模态可靠性，并且利用六西格玛概率分析得到电主轴振动可靠度指标。Lin[4]将遗传算法和蒙特卡洛法结合，提出了一种同时优化高速电主轴-轴承系统公称值和轴承位置公差值最佳的方法，并验证了该方法的有效性。Jiang和Zheng[5]利用传递矩阵法和包含离心力和陀螺力矩的滚动轴承非线性动力学模型，建立了主轴-拉杆-轴承组合的动力学模型，对主轴的临界转速和动刚度进行了系统的研究，并采用优化方法进行了优化设计。 Lin[6]通过建立主轴系统的动力学模型以求得固有频率，采用遗传算法寻找轴承的最佳安装位置以使第1阶固有频率达到最大，并通过算法验证了有效性和合理性。徐磊等[7]采用遗传算法对高液静压无心磨床砂轮主轴进行优化设计，并通过MATLAB编制程序对模型进行计算并且通过相关迭代分析了砂轮主轴的体积和刚度的变化情况。孟曙光等[8]使用有限体积法研究了各参数对动静压轴承承载特性的影响特性，采用正交实验法得到了工作参数与结构参数之间的最佳组合，并验证了其正确性。

上述研究均取得了一定的成果，但都是针对电主轴输出参数中的某单一目标进行优化，并未对电主轴的综合性能进行优化，针对以上不足，本文利用响应面法研究电主轴的尺寸参数对其静刚度、振型频率以及质量进行多目标优化分析设计。

1 主要结构及参数化三维建模

电主轴实体简化结构如图1所示，轴承选用NSK角接触球轴承，并采用一端固定，一端游动的支承方式。电动机型号为GE1073-4WJ61，额定转速为6000 r/min,最大转速为18000 r/min。

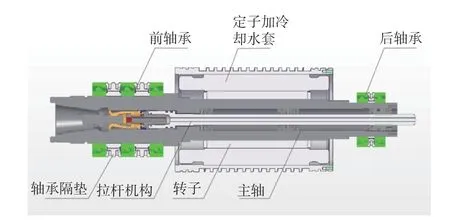
图1 电主轴实体简化模型

为了便于仿真分析和确定主轴系统的最佳结构，在建模时对实体进行了合理必要的简化[9]，将主轴悬伸量、前后轴承组之间的跨距、前端外半径和前端内半径设置为优化参数，如图2所示。

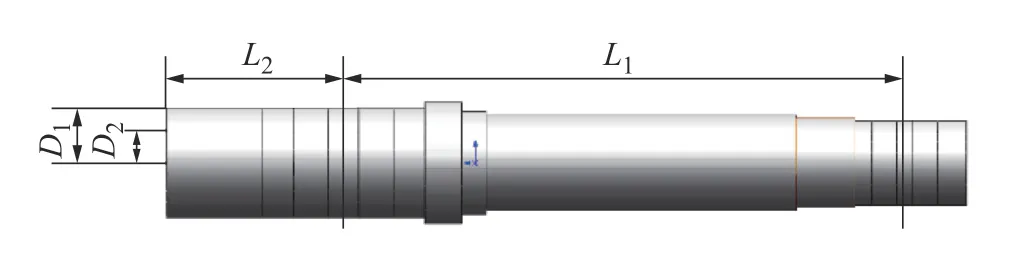
图2 主轴参数化模型

主轴参数、初始值以及各个设计因子的变化范围如表1所示, 尺寸参数变化范围为初始值的±10%。

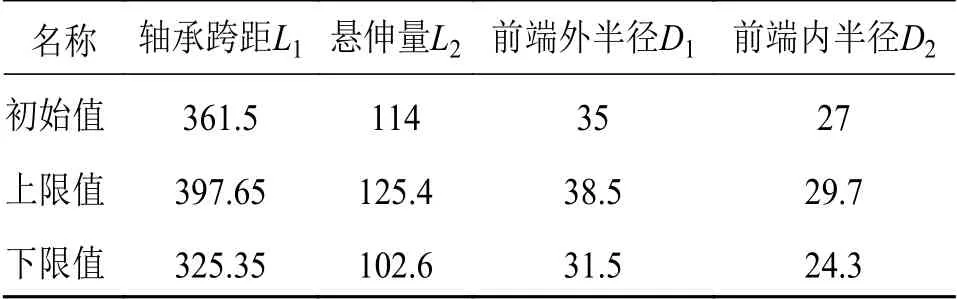
表1 尺寸参数、初始值及变化范围 mm

运用SolidWorks进行三维建模,接着在方程式中相应的的尺寸变名前输入前缀DS_,可对4个尺寸进行参数化，完成后通过CAD接口导入到Workbench中。

2 静力学分析与模态分析

电主轴的材料采用20Cr2Ni4优质合金钢，有良好的综合力学性能。该材料密度ρ =7850 kg/m3，弹性模量E= 206 GPa，泊松比μ= 0.3。根据本电主轴的电机功率为11 kW，主轴在该功率下的额定转矩T额= 17.5 Nm，作用在主轴上的最大切削力FC的计算公式为

式中：d0为主轴前端半径，d0= 35 mm。

将d0= 35 mm，T额= 17.5 Nm代入式（1），可得FC= 500 N。铣削时作用在主轴上的径向力Fr可分解为水平径向力Fh和垂直径向力Fv，工作时采用顺铣的方式，Fh/Fc的取值范围为0.35～0.40，Fv/Fc的取值范围为0.80～0.90，本次计算经验值分别取0.37和0.85，通过计算可得水平径向力Fh=185 N，垂直径向力Fv= 425 N。作用在主轴上的径向力Fr为

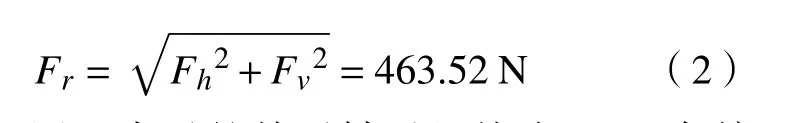
主轴上用于支承的前后轴承组均为NSK角接触球轴承，其中前轴承型号为7014C/TYNDFDLP4，后轴承型号为7010C/TYNSULP4，其中L表示预紧力的等级为轻度预紧，SU表示的是自由配组。单个角接触球轴承预紧后的径向刚度计算公式为[10]

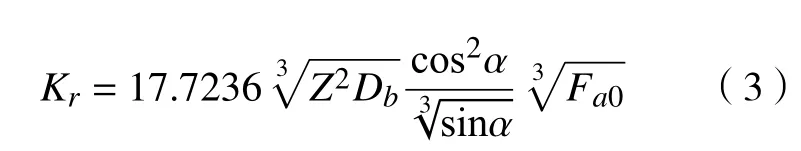
式中：Fa0为轴向预紧力，根据角接触球轴承预紧力大小的估算方法[11]，轻负荷时轴承预紧力=额定动载荷/100。

由公式（3）计算出前后轴承组的径向刚度为：

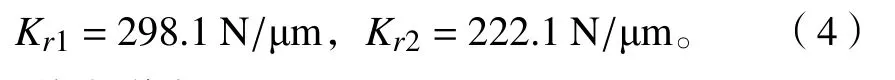
2.1 静力学有限元分析

静力学分析主要是确定主轴的静刚度，将计算得到作用在主轴上的径向切削力作为载荷条件施加在主轴前端；前后轴承组采用COMBI214单元模拟，前轴承组约束其全部自由度，后轴承组释放其轴向自由度，加载约束求解模型后，得到如图3所示的主轴静态变形图。

图3 主轴静态变形图

主轴前端的最大变形量为0.8736 μm 。则电主轴的静态刚度为

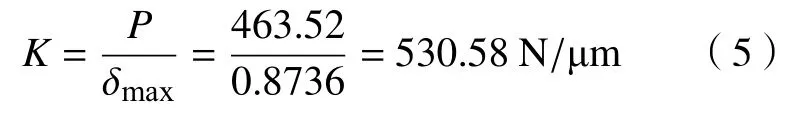
高于一般电主轴所要求的300 N/μm刚度值，所以静刚度符合要求。

2.2 模态分析

动力学分析的基础是模态分析，其主要内容是得到系统的一些固有特性（固有频率和振型等）。动力低阶模态的刚度一般来说比较弱，在受到同样大小的激励作用下，相应所占的权重相对大一些[12]。所以，在工程实际中低阶模态比较受人们的关注，用来了解结构的共振区域。对电主轴进行模态分析，网格划分和边界条件的加载同静力学分析一致，求解完成后提取电主轴的前6阶固有频率和振型，由n= 60f可得各阶的临界转速，见表2。

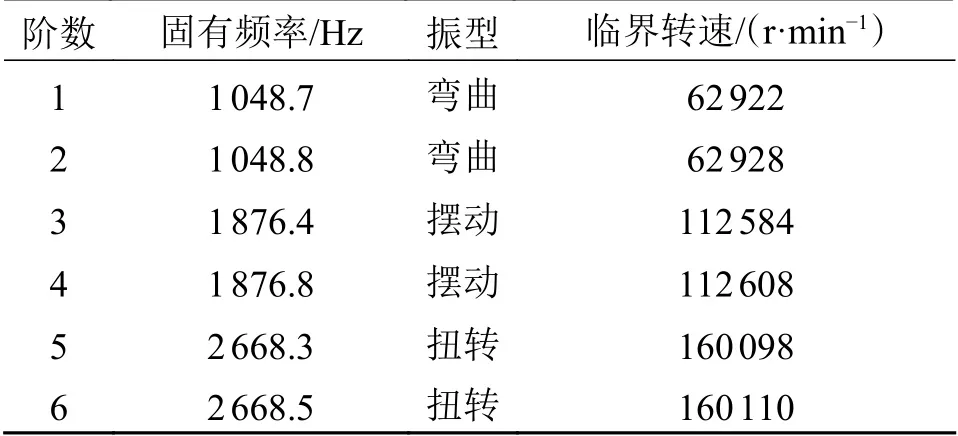
表2 前6阶固有频率、振型及临界转速

分析可得前两阶固有频率很接近，振型表现为正交，可以避免耦合现象的发生，同理3阶4阶和5阶6阶也表现为正交。由计算可知，1阶固有频率对应的转速为62922 r/min，即为主轴的1阶临界转速，本电主轴的最高工作转速为18000 r/min，远低于其1阶临界转速的75%，可以有效避免共振现象的发生。

3 参数敏感性分析与响应面建立

3.1 敏感性分析

对于一个输出参数，输入参数对它的重要性是其与这些输入参数之间的相关性所决定，而这类相关性是通过ANSYS DX的参数相关性模块研究所得到。为了研究电主轴的轴承跨距P1（表1中的L1）、主轴悬伸量P2（表1中的L2）、前端外半径P3（表1中的D1）、前端内半径P4（表1中的D2）、杨氏模量P5这5个参数对最大总变形量P6、1阶固有频率P7、质量P8的影响，在Parameters Correlation优化模块中分析得到尺寸参数对目标函数的灵敏度。计算方法采用Spearman's Rank Correlation，该方法被认为是更精确的方法，适用于具有非线性单调函数关系的变量之间的相关性。灵敏度分析结果如图4所示，灵敏度值为负数时表示随着输入参数值的增加，输出参数的值在减小。

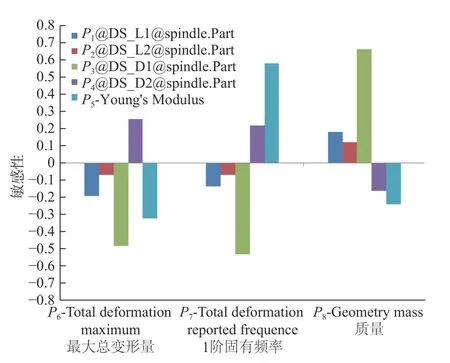
图4 敏感性分析

由分析结果可知，主轴前端外半径和杨氏模量对目标函数的影响最大，此外主轴前端内半径、轴承跨距和悬伸量对目标函数均具有相对较大的影响，因此将这4个尺寸设计参数均作为优化参数。

3.2 响应面建立

响应面方法（Response surface method，RSM）是利用实验设计法安排实验设计表，将统计学的理论引入到优化设计中，通过构建拟合代理模型来模拟各个设计变量和性能指标之间的隐式关系，它的基本思想是通过大量的确定性试验，在目标函数的下降方向寻优[13]，寻找预测的最优解及相对应的实验条件。

选择最佳填充空间（OSF）算法构建实验设计表，其优点是设计点分布均匀,可以避免聚集现象的出现。设计变量个数为4个，样本点数量为100组，通过完全二次多项式拟合方法构建响应面，部分响应面如图5所示。

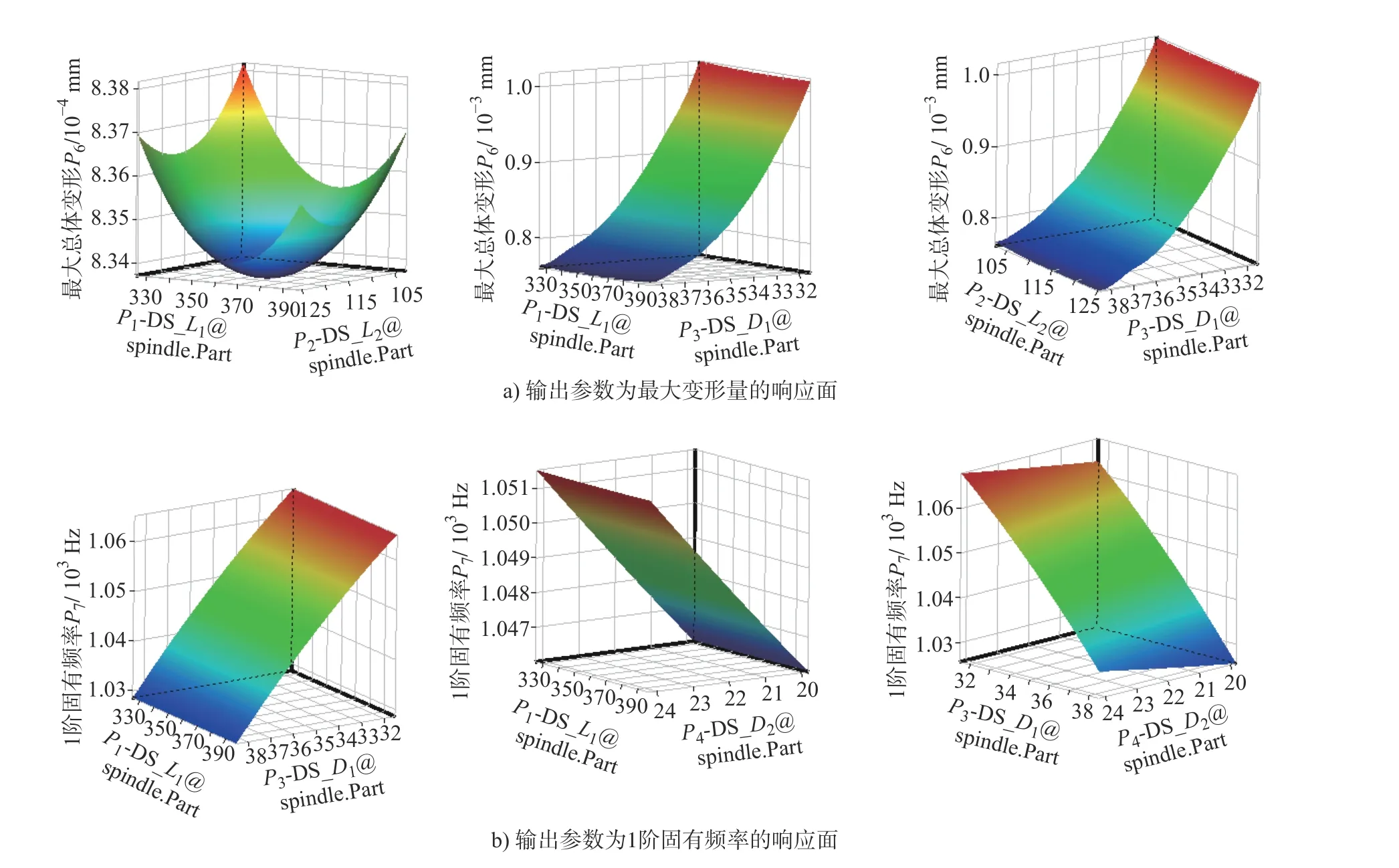
图5 响应曲面

查看响应面的拟合程度，由图6可看到，样本点几乎均在45°线上，可见响应面预测的值与实际计算值符合程度较好。

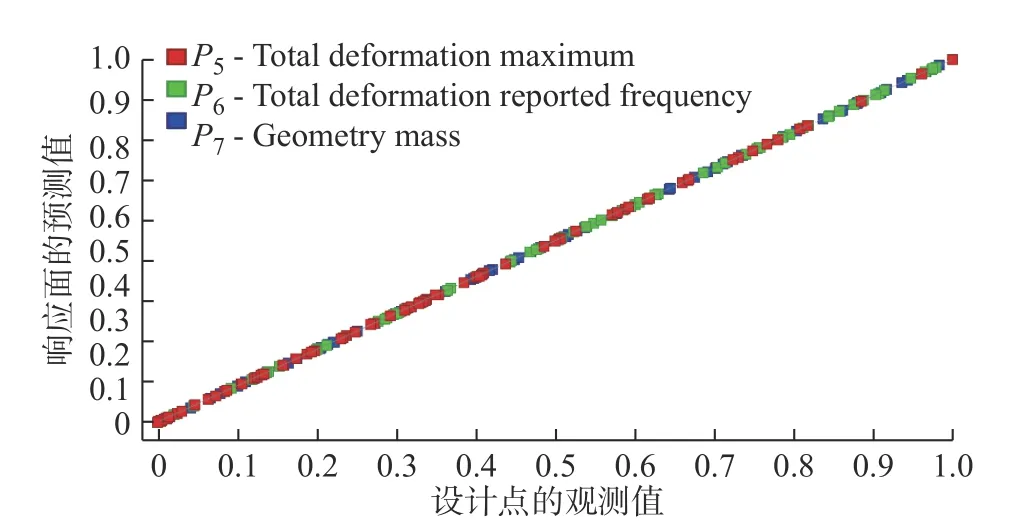
图6 Goodness of Fit拟合曲线

4 多目标优化

多目标优化是在得到响应面结果的基础上进行驱动优化，可以从响应面结果中自动获取近似的响应点作为最优的设计备选方案[14]，其优点是整个计算时间比较短，缺点是优化结果依赖于建立响应面的质量。

4.1 优化数学模型的建立

通过响应面方法得到显函数后，优化设计问题的数学模型为[15]

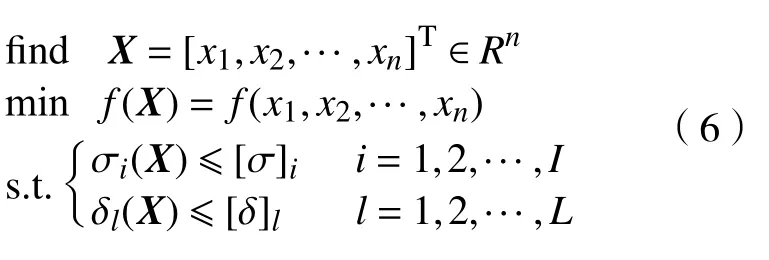
式中： find 函 数为求解的最优解；X表示设计变量；xn为 第n个 设计变量元素；Rn为设计变量的可行域；f(X)为 目标函数；s.t.为 约束函数； σi(X)为 第i个不等式约束，δl(X)为 第l个不等式约束。

电主轴优化设计通常是在满足正常工作性能的前提下达到高刚度、高频率、轻量化的目的，在所建立的实验样本中，以最大变形量最小为目标函数，1阶固有频率越大、质量越轻为约束函数，建立的电主轴优化数学模型为：

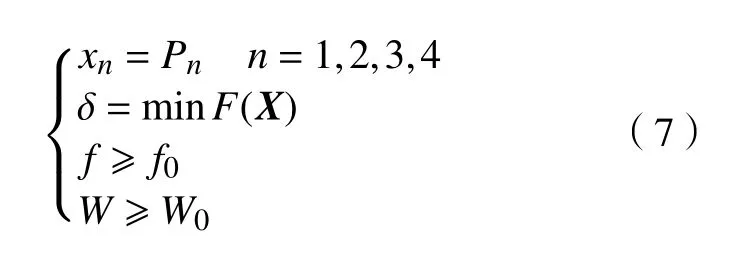
式中：Pn为 主轴设计尺寸参数；δ为主轴前端最大变形量；f0为 1阶固有频率初始值；f为1阶固有频率实验值；W为实验质量，W0为初始质量。

4.2 优化结果分析

根据设定的优化目标，选用多目标遗传算法（MOGA）进行优化，得到的一系列Pareto解如图7所示，其中Feasible points表示的是可行解。

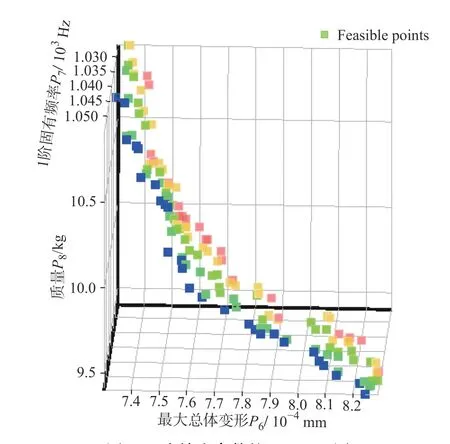
图7 3个输出参数的Tradeoff图

表3为分析后所给出的3组候选点，根据候选优化点，综合考虑优化方案的合理性，选择第3组候选参数作为优化结果，优化后静刚度由原来的530.58 N/μm变为552.89 N/μm，优化了4.2%，1阶固有频率由原来的1048.7 Hz变为1056.5 Hz，优化了7.4%，质量由原来的9.7979 kg变为9.2823 kg，优化了5.3%。

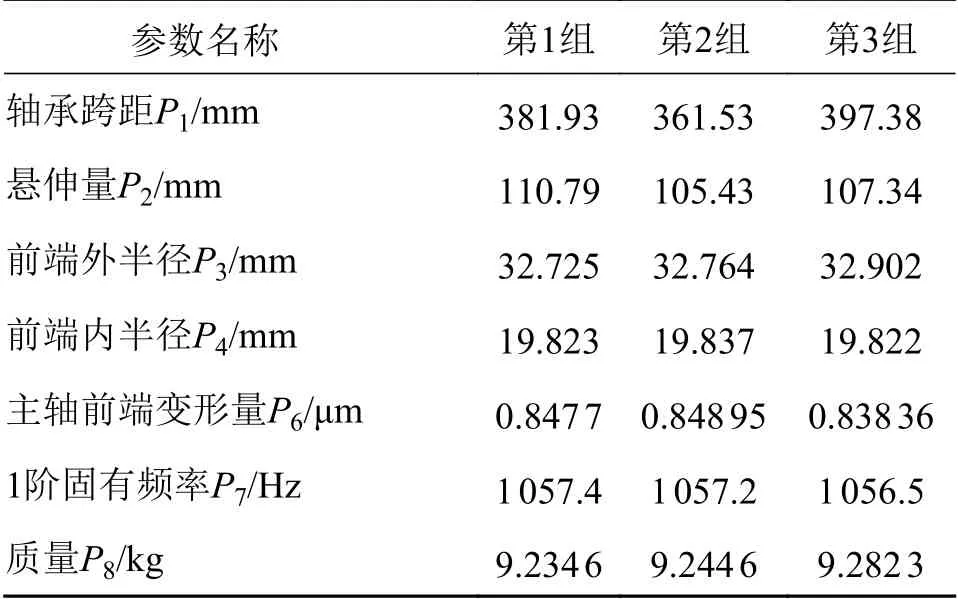
表3 优化后的3组候选点

5 结论

通过对电主轴的主要结构和关键参数进行研究分析，对模型进行合理必要的简化，首先进行静力学分析和模态分析，得到前端最大变形量、固有频率及振型情况，在此基础上对一些关键尺寸参数进行敏感性分析并建立响应面优化模型。通过多目标遗传算法对目标参数进行优化，优化后各个参数均得到了一定的改善，为相关的轴类零部件优化研究提供参考。