考虑驱动索柔性的网状天线展开动力学分析

杨癸庚，卫鑫鹏，李鹏阳，汤奥斐，孔令飞

（西安理工大学 机械与精密仪器工程学院，西安 710048）

随着航天科技的快速发展，大型星载可展开天线已经被广泛应用于电子侦察、空间通信、气象监测、导航等领域[1]，正朝着大口径、高精度、轻质量、高收纳比的方向发展[2]。在各种类型的星载天线中，环形桁架式可展开天线由于其口径大、收纳率高、面密度小等优点[3]，已成为目前研究的热点之一。

由于受到航天运载工具承载质量和容量的限制，在卫星发射阶段，天线处于收拢状态并固定在火箭整流罩内，当卫星进入预定轨道后，天线展开至工作状态。环形桁架式可展开天线是由环形桁架、张拉索网结构和驱动绳索组成的复杂多体系统，其展开过程受铰链摩擦、铰链间隙、索网张力、驱动索柔性等多种非线性因素的影响[4-6]，天线能否在轨顺利展开决定着航天器任务的成败。因此，对环形天线的展开过程进行合理的运动规划及准确的动力学分析与预测具有重要意义。

在环形天线的运动规划方面，李团结等[7]提出了匀加速-匀速-匀减速的展开过程规划，该规划过程会导致天线展开角加速度不连续，从而使天线受到较大冲击。Li[8]进一步提出了基于五次多项式的展开过程角速度规划，该方法可以在一定程度上减小加速度冲击。为了进一步降低展开过程的角加速度峰值，张逸群[9]提出了基于Bezier曲线拟合的驱动索收纳过程规划，通过设计驱动索的收纳过程实现展开角加速度峰值最小。然而，该方法基于运动学进行最优轨迹规划，并未考虑索网张力、铰链摩擦等因素对天线展开过程动力学的影响。

在考虑铰链摩擦、间隙及索网张力的展开过程动力学分析方面，Li 等[10]建立了考虑关节摩擦、微重力的含间隙空间机构刚柔耦合动力学模型，通过分析机构的展开和锁定过程，揭示了展开过程中的非线性动力学特性。该方法未考虑索网张力对展开过程的影响，分析结果与实际展开过程存在偏差。Nie等[11]、任伟峰等[12]在多刚体动力学模型的基础上，基于准静态思想，通过多项式拟合得到了展开过程中索网弹性势能与展开角之间的函数关系，进而建立了桁架-索网系统的动力学模型。Zhang等[13-14]采用弹性悬链线描述索网结构的松弛状态和张紧状态，建立了天线的柔性多体系统动力学模型，研究了展开过程中桁架铰链受到的索网张力变化规律，并通过实验验证了方法的正确性。在文献[14]的基础上，李娜[15]从能量守恒的角度出发，推导了索网张力对驱动索力和驱动功率的影响关系，并基于此进行了展开轨迹优化。然而，上述研究中，系统的动力学模型中均未建立驱动绳索，未深入研究驱动绳索的柔性对展开过程动力学的影响。

针对上述问题，本文建立了包含驱动索-滑轮系统的环形天线系统动力学模型。动力学模型中，驱动绳索采用Bushing力法进行建模，索网结构的张力等效为作用在桁架铰链上的时变外载荷。将运动学规划得到的驱动绳索最优收纳过程作为输入，对天线系统的展开过程进行了动力学分析，并通过仿真案例研究了驱动绳索的柔性、展开时间等参数对展开过程中的展开角加速度和驱动索力的影响。

1 环形桁架天线结构模型

环形桁架式可展开天线主要由环形桁架、索网结构和驱动绳索系统组成，索网结构由“背对背”的两层索网结构张拉成形，在预张力的作用下形成天线的网状反射面形状，环形桁架为索网结构提供边界支撑，如图1所示。

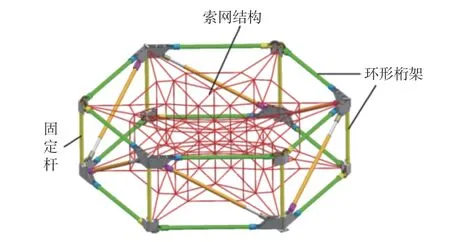
图1 环形桁架天线整体模型

环形桁架结构由一系列基本的平行四边形单元组成，每个平行四边形由两个横杆、两个竖杆、1个粗斜杆和1个细斜杆组成，如图2a）所示。驱动绳索通过导向滑轮和空心斜杆贯穿于整个环形桁架中。现有研究中[16]，大多考虑在每个五杆铰链顶点处布置一个滑轮，实现对驱动绳索的导向，如图2b）所示，该方案可以保证在完全展开状态下驱动绳索刚好通过斜杆的轴线，但是，在展开过程的中间状态会出现驱动绳索与斜杆互相干涉的现象，从而导致摩擦力增大。为了确保在整个展开过程中驱动索与斜杆不发生干涉，在每个五杆铰链处再增加两个导向滑轮，如图2c）所示。

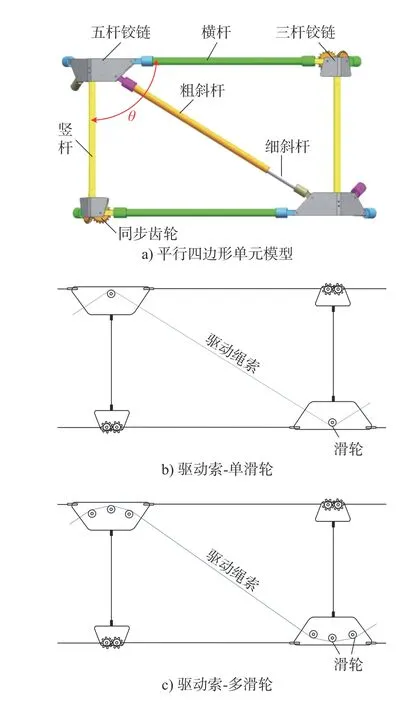
图2 环形桁架的平行四边形单元

天线的展开过程主要包含两个主要阶段：1）扭簧驱动展开阶段，天线首先处于完全收拢状态，解锁后，环形桁架在铰链处扭簧的作用下稍微弹开一个角度以摆脱自锁位置；2）电机驱动展开阶段，电机启动，通过驱动绳索来改变四边形单元对角线的长度，从而实现环形桁架展开；该过程中，随着桁架结构的展开，松弛的索网逐渐张紧，完全展开后，索网在预张力作用下形成所需的网状反射面。本文重点研究电机驱动展开阶段，该阶段环形桁架的展开过程如图3所示。

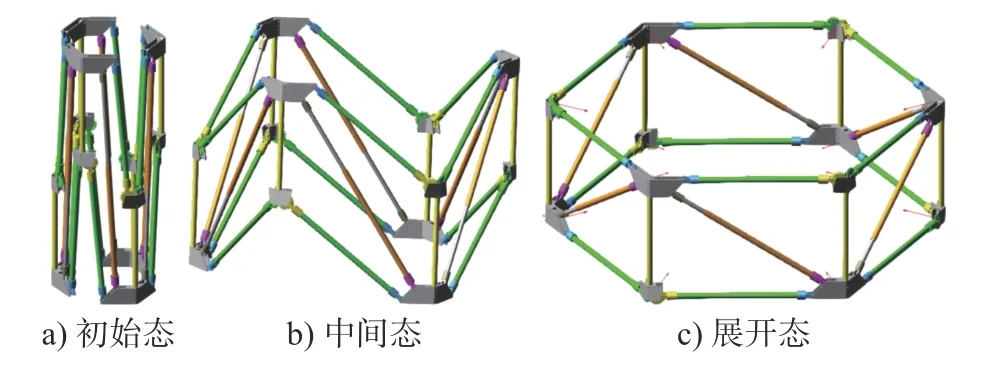
图3 环形桁架展开过程

2 运动学规划

天线展开过程中，电机通过牵引驱动绳索来改变平行四边形单元的对角线长度，从而驱动整个环形桁架实现展开。因此，根据运动学关系，将环形桁架展开过程的输出运动规划转化为对驱动索收纳过程的运动控制。

驱动索收纳长度的变化过程可用n次Bezier函数[9]表示为

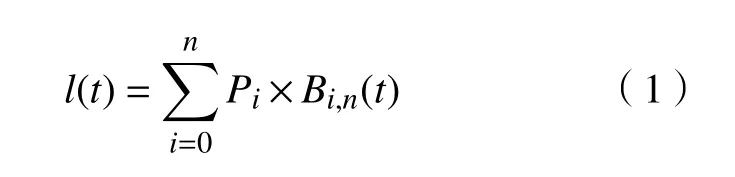
式中：Pi为 Bezier 函数的控制点；Bi,n(t)为Bezier 函数的 Bernstein 基函数。

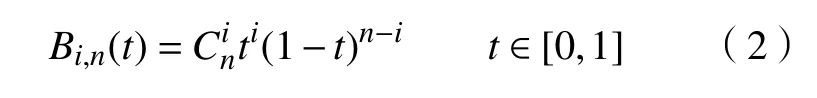
根据图2所示的基本平行四边单元的几何关系，展开角θ 的运动状态与驱动索长度l之间满足

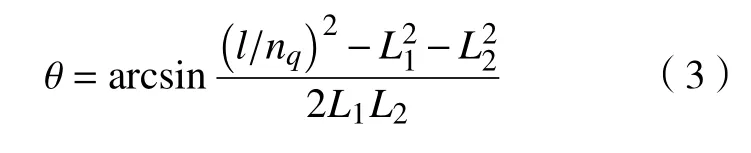
式中：nq为环形桁架的四边形单元数目；L1和L2分别为桁架的横杆和竖杆长度。展开过程中，驱动索收纳速度和 加速度可通过对式（1）求导得到，展开角速度和角加速度可通过对式（3）求导得到。

基于式（1）～式（3），可采用Bezier 函数拟合驱动索的收纳运动轨迹，并通过设计Bezier 函数的控制点参数来获取天线的最优展开轨迹。为减少天线在展开过程中的冲击力对展开精度及卫星本体的影响，将展开角加速度峰值最小化作为设计目标，同时将角速度和角加速度的连续性条件作为约束，建立优化模型如下：

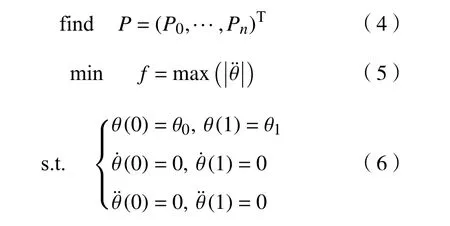
式中：θ0和θ1分别为电机驱动展开阶段的初始展开角和终止展开角，本文取θ0=5°，θ1=90°。

需指出，上述优化模型中，天线的展开总时间为广义时间1 s，当考虑实际展开时间为任意值tp时，将式（1）和式（2）中的变量t替换为t/tp即可。

3 动力学建模

本文基于多体动力学理论建立同时考虑环形桁架、驱动绳索-滑轮和索网张力的环形天线系统的展开过程动力学模型。

展开过程中，环形桁架的杆件和铰链的弹性变形较小，可视为刚体单元[12]。与桁架单元相比，驱动绳索的柔性较大，将驱动绳索离散为多个小圆柱体单元，小圆柱体单元之间采用Bushing力连接，Bushing力的计算公式为

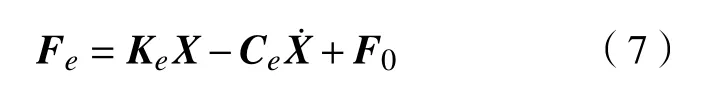
式中：Fe为 柔索单元间的受力矩阵；Ke、Ce分别为相应的刚度阵和阻尼阵；X、分别为位移和速度矢量；F0为初始受力矢量。

由图2可知，驱动索运动过程中必须经过导向滑轮，驱动索与滑轮之间的相互作用采用接触力进行约束。展开过程中滑轮的弹性变形可以忽略不计，也视为刚体单元。

综上，基于拉格朗日乘子法建立天线系统的展开过程动力学方程为

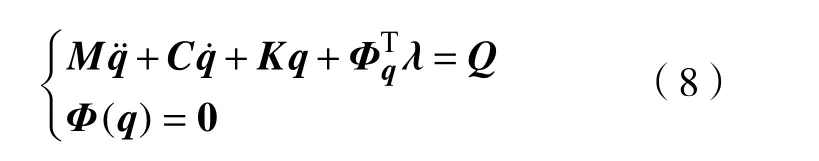
式中：q为系统的广义坐标；M为系统的质量阵；C为系统的阻尼阵；K为系统的刚度阵；λ为拉格朗日乘子； Φ(q)为 系统的约束条件；Φq为约束条件的雅克比矩阵；Q为系统受到的广义力。

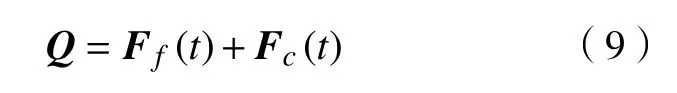
式中：Ff(t)为系统受到的摩擦力，其大小由各个铰链处的摩擦因数决定；Fc(t)为索网结构作用在桁架铰链上的时变外载荷。

Fc(t)的计算方法如下：

1）基于文献[13]，获取索网结构对桁架铰链的作用力Fc与展开角θ 之间的关系Fc(θ)；

2）根据第2节的展开过程运动规划，可得到展开角的运动规律θ(t)；

3）结合Fc(θ)与 θ(t)， 即可求得Fc(t)。

4 仿真案例

4.1 模型参数

本文对图1所示的环形桁架天线进行运动规划与动力学分析，该天线由6个平行四边形单元组成，天线口径为1 m、高度为0.3 m、前后网面焦距为0.45 m。该天线模型中，杆件的材料为碳纤维，铰链、同步齿轮和滑轮的材料为铝，索网材料为芳纶纤维，驱动绳索为钢丝绳，钢丝绳的弹性模量为200 GPa。各零部件的几何参数见表1。

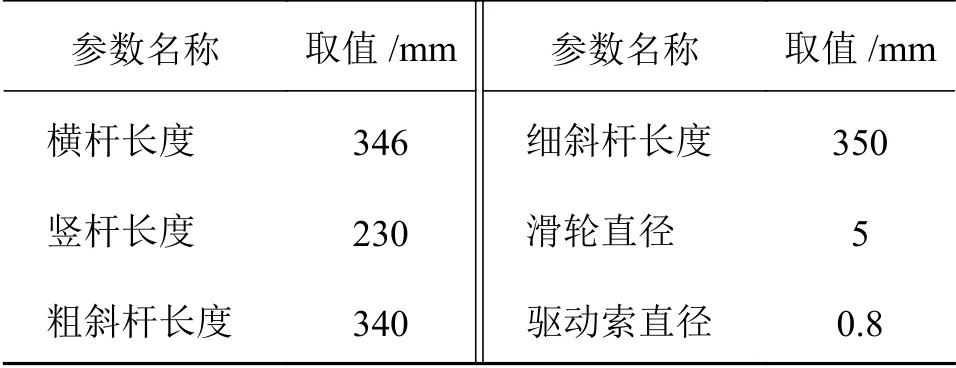
表1 零部件几何参数

4.2 运动规划

采用第2节的优化模型对天线的电机驱动展开过程进行最优运动规划。选用10阶Bezier函数拟合驱动索收纳长度的变化过程，优化得到最优解为P= （0.6403, 0.6403, 0.6403, 0.6372, 0.6303, 0.6402,0.5188, 0.5231, 0.4671, 0.4671, 0.4671）T。将最优解代入式（1）和（3）并求导，得到规划后的展开角度、角速度和角加速度如图4所示，驱动绳索的最优收纳状态如图5所示。

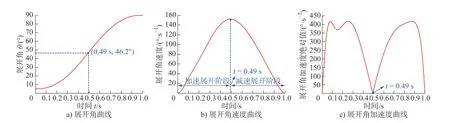
图4 展开角的最优运动状态

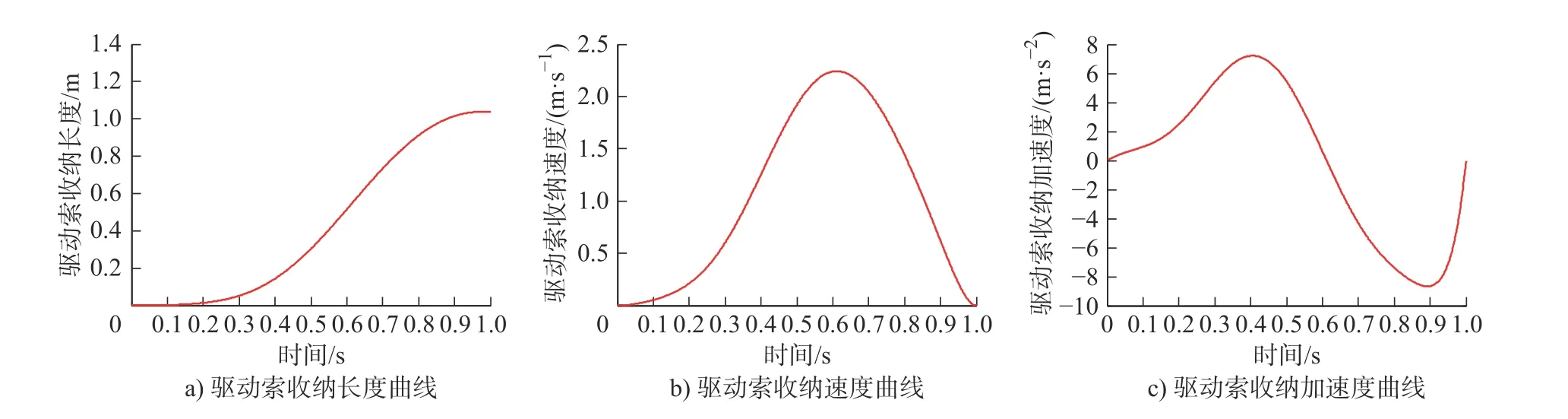
图5 驱动索的最优收纳状态

由图4可知，天线的最优展开过程可分为两个阶段：

1）加速展开阶段：展开角速度由0增加到最大值，相应的展开时间为0 ～ 0.49 s，展开角为5° ～46.2°；

2）减速展开阶段：展开角速度从最大值逐步减小到0，相应的展开时间为0.49 ～ 1 s，展开角为46.2° ～90°。加速展开阶段和减速展开阶段的加速度峰值刚好相等，均为416.9 °/s2。

4.3 动力学分析

4.3.1 计算工况

基于第3节的动力学模型，采用ADAMS软件建立环形天线的动力学仿真模型，并进行展开动力学分析。仿真模型中，以图1所示的一个竖杆为固定端，设定各个铰链之间的摩擦因数为0.07，驱动索与滑轮之间的摩擦因数为0.01。

将电机的转动角速度ωd作为驱动，可表示为

索网结构作用在桁架铰链上的作用力如图6所示。在展开角0 ～ 74.5°（展开时间0 ～ 0.7 s）的过程中，索网处于松弛状态，铰链受到的索网作用力为零，该阶段天线展开的阻力主要是摩擦力；在展开角74.5° ～ 90°（展开时间0.7 ～ 1 s）的过程中，索网逐渐张紧，该阶段天线展开的阻力包括摩擦力和桁架铰链受到的索网力。

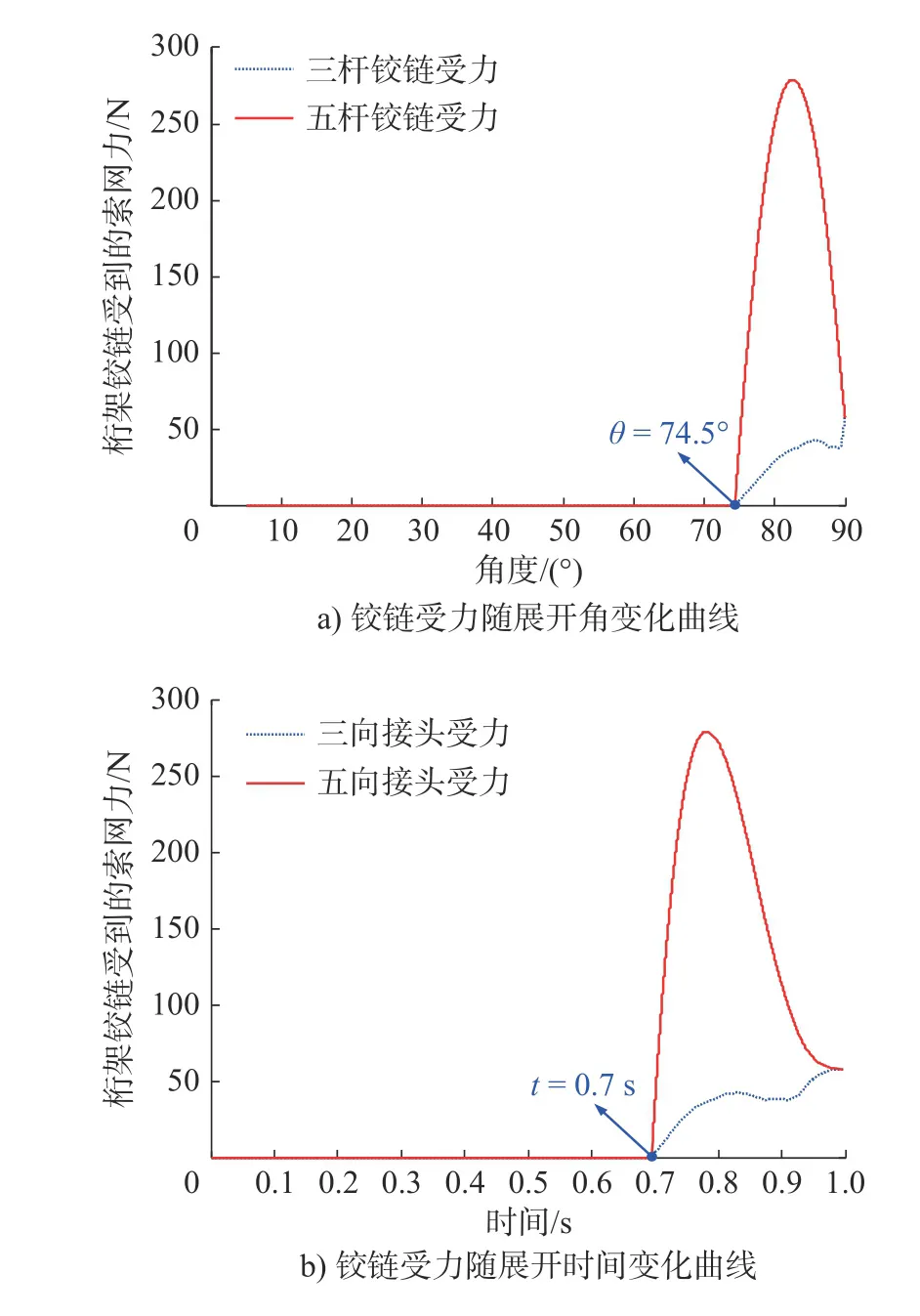
图6 桁架铰链受到的索网作用力曲线

4.3.2 结果分析

为分析绳索柔性对天线展开过程的影响，在其它参数保持不变的情况下，针对驱动索弹性模量为50 GPa、100 GPa、150 GPa、200 GPa和250 GPa这5种情况，分别对天线展开过程进行了动力学求解。天线展开角加速度和驱动索力曲线分别如图7和图8所示。不同驱动索弹性模量下，天线展开角加速度峰值和驱动索力峰值见表2和表3。

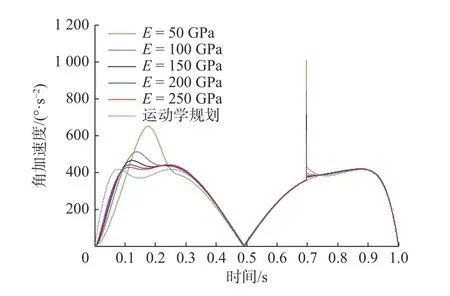
图7 不同驱动索弹性模量下的展开角加速度曲线

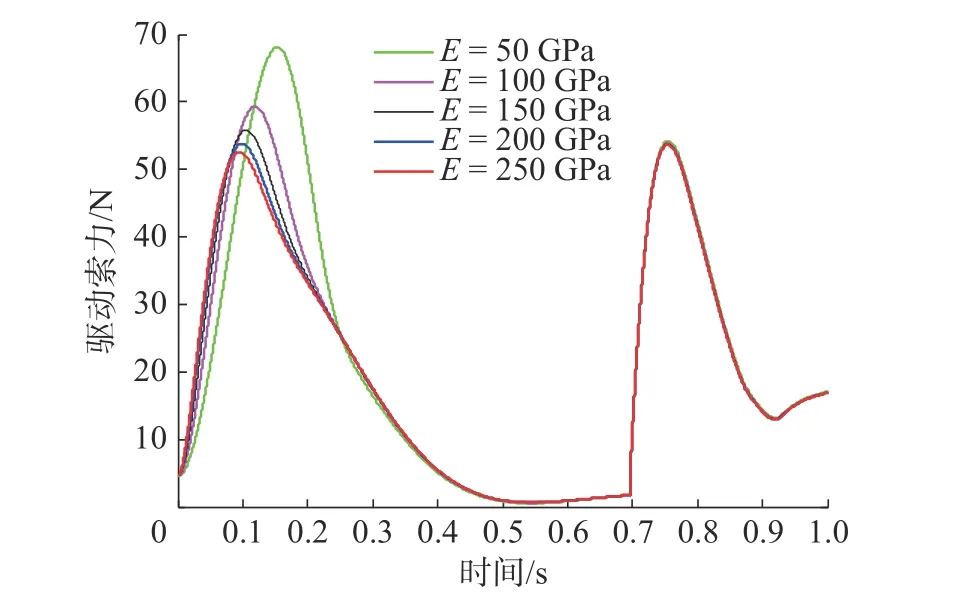
图8 不同驱动索弹性模量下的驱动索力曲线

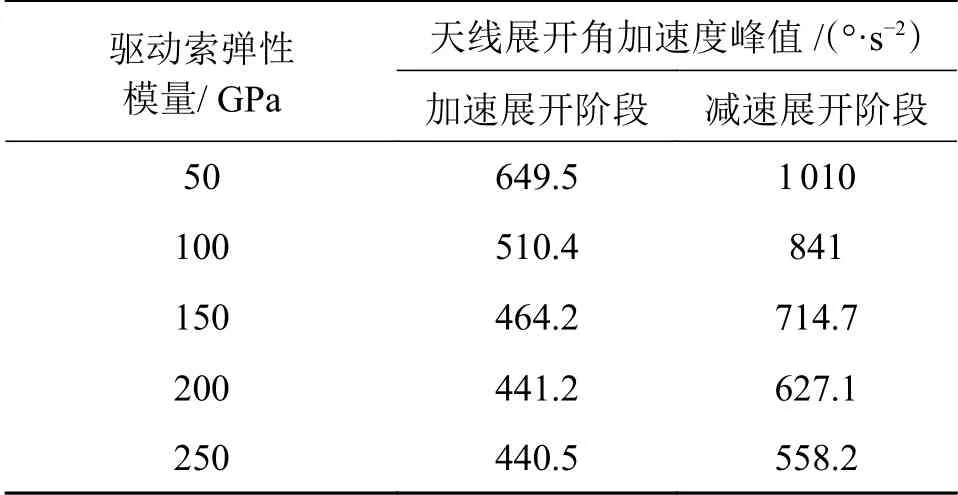
表2 不同驱动索弹性模量下的天线展开角加速度峰值

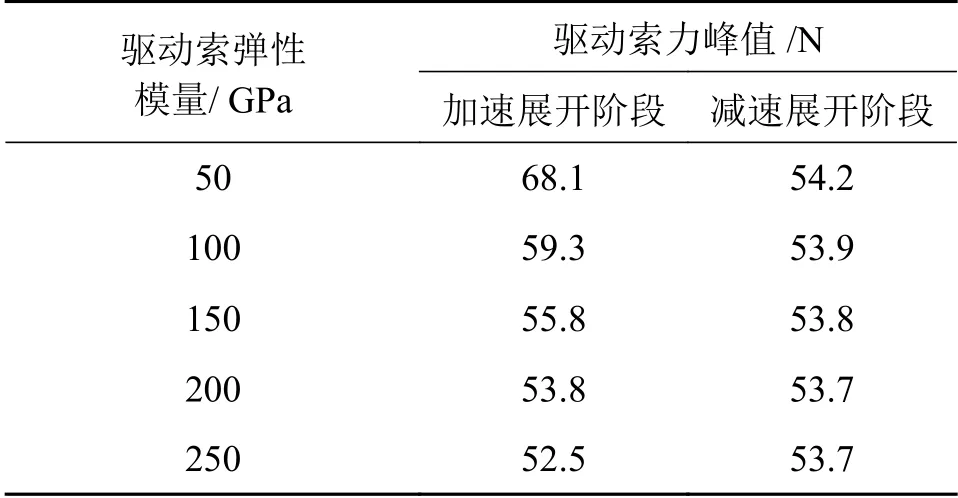
表3 不同驱动索弹性模量下的驱动索力峰值

由图7可知，由于动力学分析中考虑到桁架铰链会突然受到索网张力作用，导致展开角加速度出现了明显的突变。结合图7和表2可知，驱动索的弹性模量对天线加速展开阶段和减速展开阶段的角加速度峰值均会产生显著影响，驱动索的弹性模量越大越有利于减小展开过程中的角加速度峰值。随着驱动索弹性模量不断增大，其对展开角加速度的影响将逐渐趋于稳定。

由图8可知，驱动索力在加速展开阶段和减速展开阶段各出现了一次峰值。加速展开阶段驱动索力出现峰值的原因是展开前期驱动索力既要克服摩擦阻力又要提供天线桁架展开所需的动能；减速展开阶段驱动索力出现峰值的原因是展开中后期桁架铰链会受到索网张力的作用，驱动绳索需要克服摩擦阻力和索网张力的共同作用。

结合图8和表3可知，驱动索的弹性模量对减速展开阶段的驱动索力影响较小，但对加速展开阶段的驱动索力影响显著，驱动索的弹性模量越大越有利于减小展开过程中的驱动索力峰值。随着驱动索弹性模量不断增大，其对驱动索力的影响也将逐渐趋于稳定。

为分析天线的展开总时间tp对展开角加速度和驱动索力的影响，在驱动索弹性模量为200 GPa的条件下，进一步对展开时间分别为10 s和100 s的天线展开过程进行了动力学求解。不同展开时间下，展开角加速度和驱动索力曲线分别如图9和图10所示，展开角加速度峰值结果见表4。

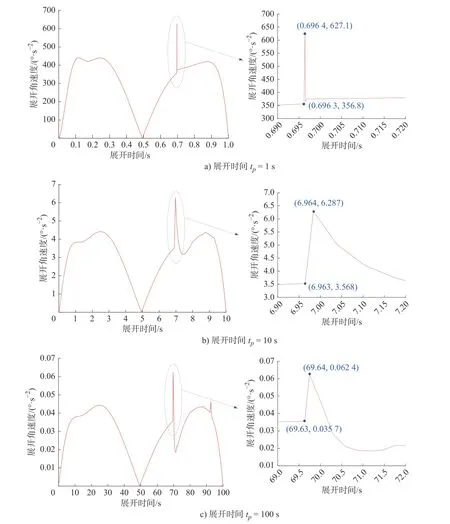
图9 不同展开时间下的展开角加速度曲线

由图9可知，展开时间对展开角加速度的影响非常大，整个展开过程中的展开角加速度值随着展开时间增大而减小。结合图9和表4可知，展开角加速度峰值与展开时间tp的平方近似成反比。

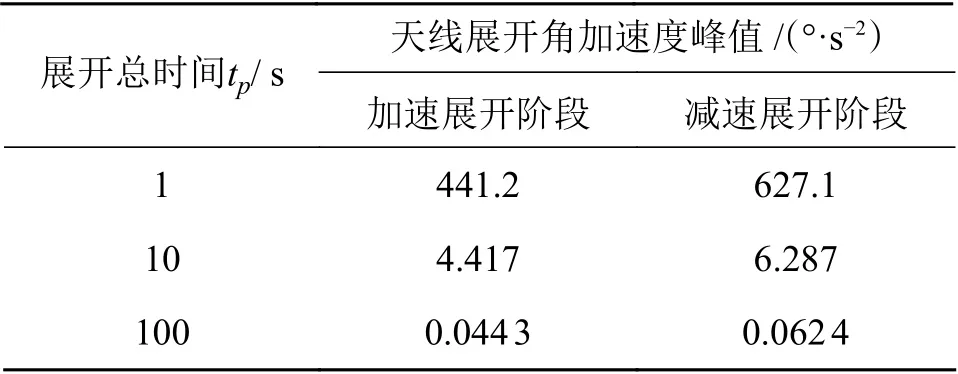
表4 不同展开时间下的天线展开角加速度峰值

由图10可知，展开时间主要影响索网松弛阶段（展开角0 ～ 74.5°）的驱动索力，对索网张紧阶段（展开角74.5° ～ 90°）的驱动索力影响较小。随着展开时间不断增长，索网松弛阶段的驱动索力将逐渐减小最终趋于稳定值。另外，tp=10 s和tp=100 s的驱动索力接近，且比tp=1 s的驱动索力小得多，其原因是展开时间越短，短时间内驱动索需要提供的天线展开所需的动能越大。综上，从降低展开角加速度峰值的角度出发，展开时间越长越好；而从降低驱动索力的角度出发，展开时间足够长之后，驱动索力将趋于稳定。

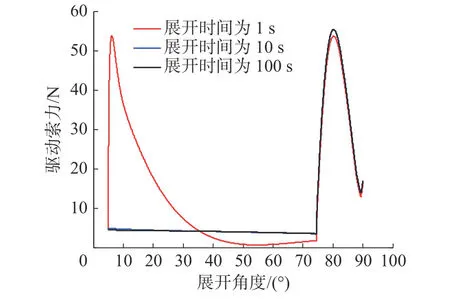
图10 不同展开时间下的驱动索力曲线

5 结论

1） 驱动索柔性对加速展开和减速展开阶段的展开角加速度值均有较大影响，而对驱动索力的影响主要体现在加速展开阶段。

2） 展开时间对整个展开过程中的展开角加速度值影响均较大，而对驱动索力的影响主要体现在索网松弛阶段。