基于十六叉树-多尺度表达R树的TGIS时空数据索引算法

马 龙 姜 岚 张正义 程庆荣

1(西安航空学院经济管理学院 陕西 西安 710077) 2(西安航空学院计算机学院 陕西 西安 710077)

0 引 言

随着时态地理信息系统(Time Geographic Information System,TGIS)在现代智能交通、车辆轨迹监测和图像处理等诸多领域的广泛应用，该系统在应用过程中产生的数据量大，数据结构复杂，数据表达形式多样化，用户访问数据量大。然而，为了解决多用户视角下TGIS时空数据索引需求，支持多维、多分辨率及多尺度时空数据存储表达与索引问题成为当前地理信息科学研究领域普遍关注的焦点[1-3]。

多维、多分辨率及多尺度时空数据存储表达与索引处理问题复杂、技术难度大、研究范围广，但从当前研究成果来看，主要从三个方面展开：第一个方面是如何利用分块或扩展八叉树存储方法对多分辨率空间数据进行组织管理，其中从八叉树存储空间大小角度考虑多分辨率空间数据的表达问题较为普遍[4-7]，且表达空间数据的结构主要以指针或线性八叉树数据结构为主，但这会造成内存资源消耗大、对地理信息系统的硬件资源要求高，特别是三维八叉树数据结构只能对空间数据进行有效表达，而对于时间上动态变化的增量数据表达问题却无法表达和存储；第二个方面是如何实现多维空间数据索引方法，其中主要从三维空间R树或扩展R树来表达多维空间数据[8-10]，但这类索引方法对于多维时空数据时索引效率较低；第三个方面是如何实现多尺度空间数据表达、处理与索引问题，其中主要从制图理论、综合算法模型和四叉树索引结构等方法进行研究[11-14]，但这些方法解决多尺度空间数据时效率较低，无法满足多用户多视角下时态地理数据信息增量索引的需求。因此，如何同时将多维度、多尺度和多分辨率的空间数据与时态数据进行有效融合、统一存储和整体表达，达到TGIS中的时空数据动态索引和按需访问，解决当前TGIS应用环境中的多源时空数据的动态管控问题具有重要的研究意义。

综上可知，为了实现上述多维度、多尺度和多分辨率时空数据的存储和索引问题，本文利用十六叉树和多尺度表达的R树索引结构，构建基于四维十六叉树和多尺度表达R树的时空索引结构4DHMSR(4D Hex tree & Multi-Scale representation R tree integrated spatiotemporal index)树，提出多维、多尺度和多分辨率数据存储空间划分与索引算法，实现TGIS中时空数据的统一存储和索引访问，提高TGIS在不同应用领域中时空数据的存储和索引效率。

1 时空数据索引结构分析

1.1 十六叉树结构

十六叉树(Hex Tree，HT)结构最早是由Joshi在1988年提出[16]，经过不断的实践应用和优化，该方法成为移动对象和TGIS数据索引的关键技术。文献[7]采用线性十六叉树结构，解决了矿山GIS时空数据模型表达问题，但对于时空数据的存储计算空间较大，无法降低时空数据计算量。由此本文作者利用十六叉树索引结构，将随时态变化的空间划分为诸多相同尺度的块体单元(时空体元)中的数据存储量进行计算，提出了时空体元编解码存储的低计算量优化算法，较好地解决了上述占用存储空间大的问题[17]。实践证明其对海量多维、多分辨率时空数据索引、查询具有突出的特点，因此利用四维十六叉树结构建立时空数据索引是符合多维度、多分辨率时空数据检索要求。如图1(a)所示，对目标对象进行索引时，分辨率为3，时空位置上的块体被划分为3个基本正方体，用十六叉树结构表示为两个不同的分支，图1(b)为十六叉树体元划分图解。本文主要从编码原理、时空体元划分和搜索方法三个方面对十六叉结构进行详细阐述。

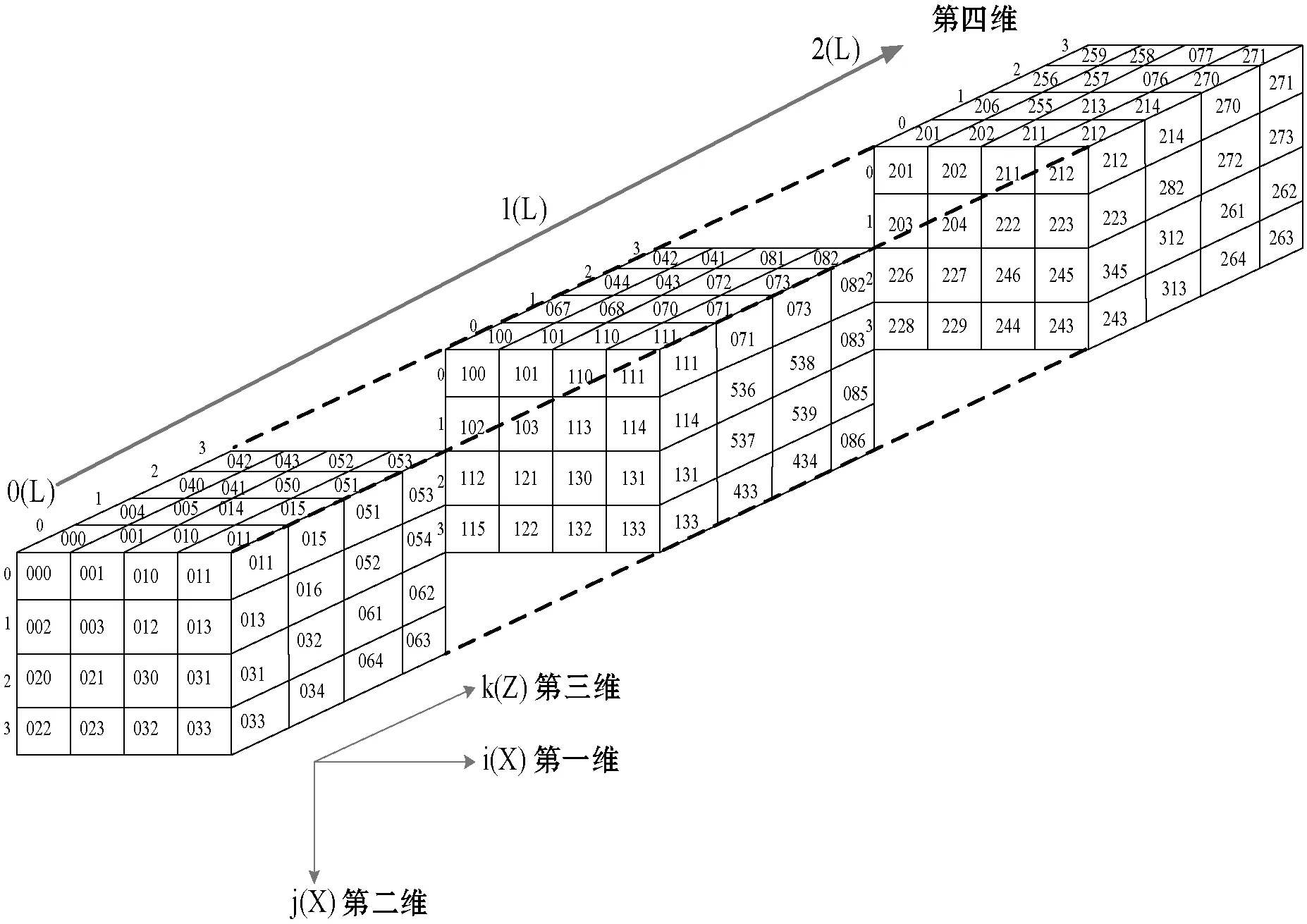
(a) 十六叉树编码图解[7](n=3)

(b) 十六叉树体元划分图解图1 十六叉树结构示意图

十六叉树的编码原理：首先，将重要的目标节点用7为基数来编码，称为定位码，定位码的位数表达了分辨率的大小或目标的划分程度，并且根据定位码来确定搜索目标的坐标位置，称为编码；其次，根据目标对象的坐标位置来确定定位码，称为解码；最后，利用定位码的编解码解算规则，计算出定位码的具体数值。其定位码的计算规则为：① 给定分辨率，确定坐标系统大小和体元编码的位数；② 对于整个原始体元编码按照乙字型方向进行编码，其方向与选取的四维坐标有关。根据图1(a)编码图解可知，该索引结构对于空间体元对象标识与地理时空坐标位置存在严格的对应关系[7]。

十六叉的体元划分原理与八叉树的对象划分原理基本类似，只是八叉树用于表达三维空间目标，而十六叉树用于表达四维时空目，且所有构成八叉树的规则均符合十六叉的构造原则。十六叉树体元划分的基本原理是：构造一个正方体区域，该区域是包含固定时间段内所有空间目标的最小边界，定义为原始体元，将有界的目标不断分解成十六个大小相等的子目标，每个子目标都有固定的边界，分解的层级深度与目标的表示越精细，所有最深分解层次上的分支目标属于叶子节点，它们属于同一个层次，且达到所需的分辨率要求。分解的结果类似一棵倒立的层次树，树的内部节点上涵盖十六个孩子节点[7]。

十六叉树的搜索原理：每棵十六叉树是由父节点和孩子节点构成，每个父节点涵盖16个子节点，叶子节点对应查找表项，子节点代表读入的搜索路径，在十六叉树搜索法中，首先确定查找表的基地址，然后读取4 bit的体元，求出基地址和体元的并集，得到当前查找节点的地址，如果此节点为叶子节点，则终止搜索过程，否则继续搜索，如此递归地搜索[18]。

1.2 多尺度表达的R树

多尺度表达的R树(Multi Scale represented R Tree，MSR树)是R树的一种改进形式，MSR树是N+1维(N是空间维数，1是分辨率维度)的R树，基本思想：首先利用R树表达实体对象的重要度因子[19]将实体对象进行等级划分，并将分辨率较低的视图对象数据删除，且在对象表达过程中引入显示分辨率维，利用MSR树的深度遍历层次的树型来表达多尺度空间数据的变化分辨率；其次使用MSR树的上层树形结构来表达空间实体对象；最后为了使实际地理空间特征与所表达的树形分支结果相符合，需考虑地理空间对象间的关联性，这样采用综合算法来实现多尺度空间数据索引问题[20]。

根据图2(a)中MSR树的矩形分块可以看出，在树形分支R12中的空间对象要素A与树形分支R16中的空间对象要素B均属于树形分支R6。首先，根据MSR树的基本思想，为了使实际地理空间特征与所表达的树形分支结果相符合，需考虑到地理空间对象要素之间的关联关系、要素与周围环境的语义关系，这样可使用综合算法将空间对象要素A和B进行合并操作。然后，利用空间对象要素的分裂算法，将树形分支R6进行分裂成孩子节点，并利用插入算法将树形分支R12插入R6分支节点内，这样可完成空间对象要素A和B的合并操作。图2(b)中的R12与R16虽然被调整到同一个分支下面，但是前期的插入、划分和整合过程的时空复杂度依然没有降低。

(a) MSR树矩形分块结果

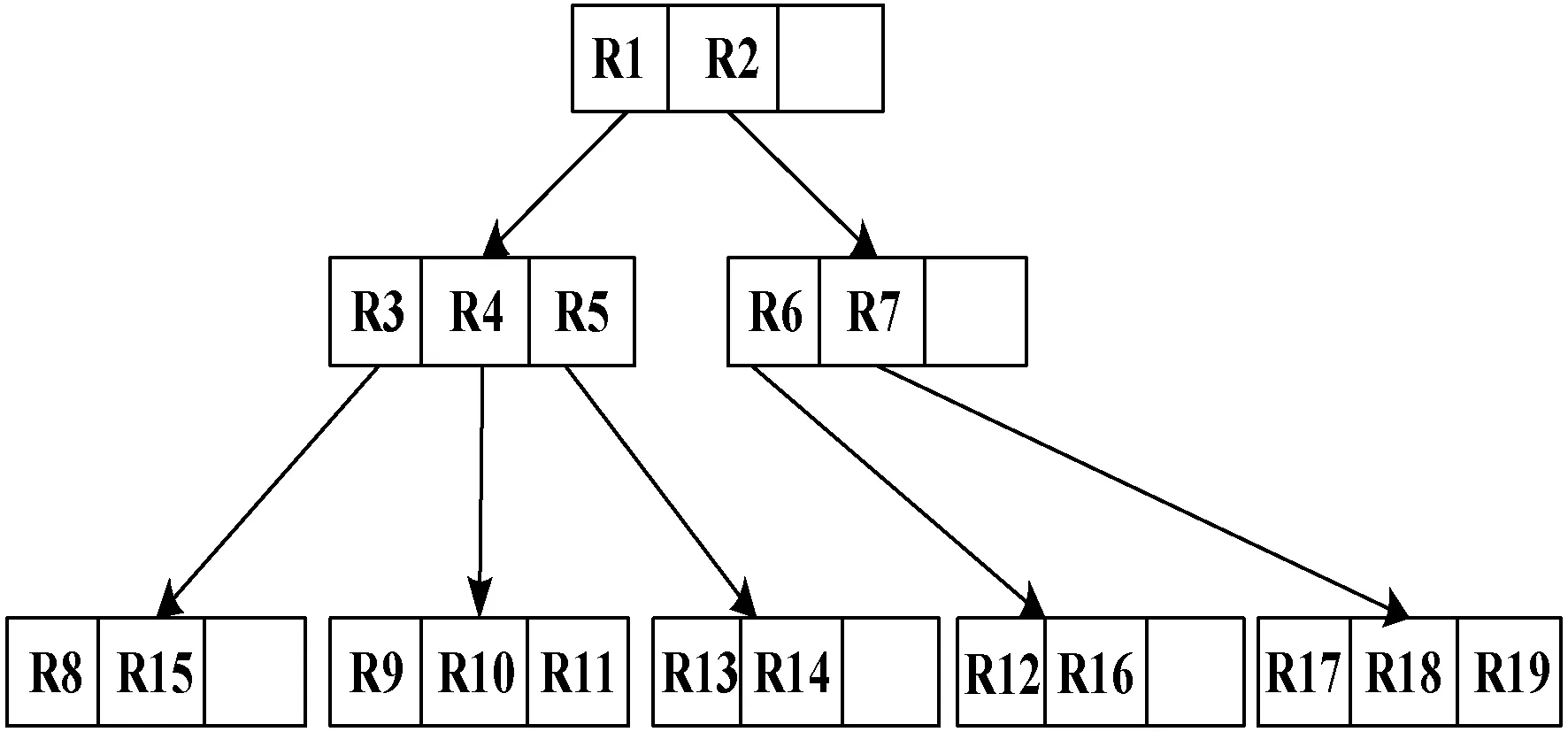
(b) MSR树结构图2 MSR树的基本结构[19]

2 4DHMSR树

2.1 算法思路和多尺度表达的时空索引方法

根据上述MSR树本身存在的问题可知，索引方法通常受到创建效率、存储空间、索引时间等多种指标的影响[10]。为了满足时空对象增量数据索引的要求，采用4DHMSR树构建时空数据多尺度索引和查询方法。4DHMSR树数据结构采用嵌套的二级索引组织形式，其中MR树为一级索引结构，四维十六叉树为二级数据结构。该嵌套树形结构既可充分利用十六叉树快速收敛和划分特性，也具有MSR树在多维空间中的高效检索特性。图3是4DHMSR树数据结构的组织结构图。

图3 4DHMSR树数据结构的组织结构[19]

4DHMSR树的基本原理：将空间对象按照空间认知的方法划分为n个不同分辨率的子视图V1,V2,…,Vn，则构成图3所示的时空数据多尺度索引的坐标轴，其中V1,V2,…,Vn分别用分辨率轴上的一个坐标点进行刻画，坐标点的位置由具有Vi分辨率时空对象的最深层次节点确定。当时空对象的现时分辨率介于{Vi,Vj}时，则Vi,Vj之间某一节点单元可直接指向时空目标对象，当要查询某目标区域S内分辨率为Vj的子视图时，只需对存储在十六叉树中小于等于Vj分辨率的空间对象和Vj+1的综合索引结果进行直接查询；其次对子MSR树的搜索对象和时空对象节点的位置以及Vj深度子树的查询进行索引。其具体的索引流程如图4所示。

图4 4DHMSR树多尺度索引流程图

在4DHMSR树中，MSR树是一个N+1维(N是空间维数，1是多分辨率维)的多尺度表达的时空R树(Spatiotemporal Tree Multi-Scale Representation，STMSR)附件时间属性特征的树形结构，STMSR树节点最小包围盒(Minimal Bounding Rectangle,MBR)是其孩子节点Childi集合的时空坐标轴最小范围，以秒为时间单位。目标索引节点打包作为STMSR树的叶子节点，将其索引项插入叶子节点的上一层中，利用节点选择和节点分裂子算法优化STMSR树结构。由于采用STMSR树对某个时间段内目标对象的空间位置的搜索效率较低，为此，将目标对象标识符OID和起始时间tStartTime构造成一维关键码(OID+StartTime)，作为索引目标节点的索引项，借助十六叉树结构[7]的海量多维数据索引能力，对时空区域内目标对象的位置进行定位，利用十六叉树兄弟节点间的指针关系进行追根溯源，确定父子节点与时空坐标间的关系。

2.2 算法流程与存储设计

2.2.1STMSR树的评价指标

鉴于多维、多分辨率的时空数据索引的综合考虑，在空间对象上采用MBR划分为规则块，在时间粒度上采用文献[21-22]的思路，本文提出评价指标的数学表达式如下：

(1)

式中：Si表示节点空间坐标区间；R表示多分辨率坐标轴；T表示时间坐标轴区间。

选择该评价指标是以三维柯西值不等式为依据：

(2)

2.2.24DHMSR树生成算法

STMSR树型结构可对多种数据类型进行查询，但是每个目标节点数据都要经过节点选择和节点分裂等复杂的操作才能插入到索引结构中，这在TGIS中实现动态数据索引较为困难。因此采用一种动态方式构建时空4DHMSR树索引结构，并给出索引创建算法、插入与分裂算法的描述和算法流程，如图5、图6所示。

图5 4DHMSR树的创建流程

图6 选择节点的子算法流程

4DHMSR树的索引创建算法是给STMSR树设定扇出(fanout)参数，即每个目标节点数据允许包含最大元组数目和最小元组数目，十六叉树结构的分裂过程中，满足扇出参数条件的子节点将重新计算时空变化范围，以叶子节点形式插入到STMSR树结构中。目标节点数目小于扇出参数最小值的子节点输出至数组，将满足扇出参数的叶子节点按序逐一插入到STMSR树，该过程中不会对数组中的点重新排序，因为这些时空变化的点几乎相邻。而将不满足扇出参数的叶子节点加载到全局节点数组中，当十六叉树结构分裂结束时，即可确定目标对象的时空位置，然后采用单点插入的形式将目标对象对应的节点逐个插入到STMSR树形结构。

算法14DHMSR树的时空索引创建算法。

算法输入：目标属性数据元组集合，STMSR树扇出参数为[imin,imax]。

算法输出：4DHMSR树的索引结构。

步骤1计算给定时间坐标轴区间T内包含所有目标属性数据集的最小包围盒{min(X,Y,Z,T),max(X,Y,Z,T)}并以min(X,Y,Z,T)作为时空对象的起算点，全部点集均是根节点node中的元组，并创建两个节点数组Array1和Array2。

步骤2如果元组数目大于imax，则将给定时间区间内的空间均匀划分八个二级子立方体，每个子立方体中包含8个孩子节点Childi(i=0,1,2,…,7),并将目标节点分配至对应的分支节点上，进入步骤3；如果根节点node中元组数目小于等于imax，则停止分裂。

步骤3清空Array1，逐个遍历子节点Childi，如果Childi中的节点数目小于imin，将其中的点加入到Array1中，并令Array1中的节点数目为iStNum，进入步骤4。

步骤5逐个遍历子立方体中的孩子节点Childi，如果Childi节点数目大于imax，则令根节点node为Childi，进入步骤2。

步骤6广度遍历孩子节点Childi，如果Childi介于[imin,imax]，则将所有孩子节点逐个插入到STMSR树的叶子节点。

步骤7所有四维十六叉树结构分裂结束后，将Array2中的目标节点以元组形式逐个插入到STMSR树。

步骤8索引构建结束。

算法24DHMSR树的动态插入和分裂算法

算法输入：准备插入4DHMSR树中的目标节点数据集，已经建立的4DHMSR树索引结构，将要索引目标节点标识的索引结束时间阈值Toendt，清除缓存内已访问节点的时间阈值Tcnode。

算法输出：更新后的数据索引结构。

步骤1根据目标节点存储数组Array2中的访问对象，将该对象标识符OID作为访问关键码，查找对应的目标节点数据，相对于找到目标节点的结束时间tEndTime，如果查找目标节点所经历的时间区间time超出了时间阈值T，进入步骤(2)；否则，将目标节点数据集插入到STMSR树中，并更新数组Array1，如果数组Array1已满，进入步骤2，否则，进入步骤6。

步骤2利用选择节点的子算法流程(如图6所示)，为待访问节点node确定插入STMSR树的父节点Father，插入node后，如果导致节点大于imax，则采用节点分裂子算法将node节点分为二级子立方体，如果导致该节点node对应的父节点大于imax，则采用节点分裂递归算法处理，否则，将节点转入Array2数组中，如果数组中的节点数目iStNum小于imin，则将Array1中的节点逐个插入到数组Array2中，直至数组Array1中的节点全部转出。

步骤3将访问的目标对象节点OID和节点开始访问时间tStartTime的组合为一个关键码添加到十六叉树存储结构中，形成新型的数据索引项。

步骤4对于生成的新节点，将其待插入目标节点插入到STMR树结构中，并由其节点代替Array1数组中OID对应的node节点。

步骤5将主缓冲区中存储的STMSR树的节点数目Nodesnum进行读取，当节点数据Nodesnum大于给定阈值，则对缓冲区中未访问节点从根节点开始清除。

步骤6算法终止。

2.2.34DHMSR树索引存储设计

多维、多分辨率和多尺度表达的海量时空数据呈指数级增加，使得时变数据管理方法需要大数据与云存储技术实现[23-25]。由此，对于独立存储在数据集中的4DHMSR树索引结构而言，可通过时空索引数据集的名称可对不同的索引信息进行辨识。对于实现多维、多分辨率和多尺度的索引的4DHMSR树而言，其索引元至少要包括数据库、数据集、索引数据集、时空维度、分辨率维度、扇出参数、叶子节点数目及根节点指针编号等目标对象标识名称。4DHMSR树形结构中的根节点指针编号是访问存储文档的唯一标识，通过根节点指针的编号从数据库中读取根节点存储数据[2,20]，进而可对4DHMSR树中的任意节点数据进行遍历。为了便于查找时空索引的元数据，除了索引的元数据外，4DHMSR树中的非根节点也被作为文档存储在数据集中。为了提升存储空间的利用效率，本文将4DHMSR树形结构中的子节点数据与元组信息集进行压缩，用一种十六进制块Hexademical data类型的数据形式存储文档，从而减少数据存储位数和空间，在实际存储时，通过进制转换实现存储需要。同时，将目标对象标识与目标节点数据集记录在叶子节点中，而将子节点的时空范围记录在非叶子节点中，从而通过从父节点遍历树结构便可得知子节点的查询索引要求是否满足。

3 工程应用与结果分析

3.1 实验环境与数据来源

为了验证4DHMSR树的索引性能，以某大型露天矿部分采场区域内不同比例尺的运输道路数据为例，采用Visual C++ 2010实现了本文的4DHMSR树生成算法，算法运行环境为64位的Windows 7和MongoDB数据库，Intel core I5- 760m 3.0 GHz CPU，16 GB主存和500 GB外存。以下实验数据页面大小设置为3 KB，十六叉树结构的最大分裂参数为100，时空R树的扇出参数为40和100，时间属性则是根据采场的开采进度计划时间来进行赋值，数据类型为64位整数类型。使用Brinkhoff时空数据生成器形成相同时空对象数目，从而产生不同尺度下的数据集[26]，如表1所示。通过比较比例尺为1 ∶200 000至1 ∶400 000的多维、多分辨率时空数据的显示结果发现，它们具有相同的时间点数目为1 000，空间区域值{xmin,xmax,ymin,ymax,zmin,zmax}={281,3 935,23 854,30 851,32 516,36 193}。

表1 实验样本数据集

3.2 时空索引创建性能与耗费指标分析

表2 索引耗费时空复杂性比较

从表2中可知，因为树中节点可以记录综合结果，采用4DHMSR树对相同比例尺下的时空数据经过多次的索引后，下一次索引查询的时间明显低于上一次的查询时间。另外在进行更低的多分辨率查询时，上一次多分辨率的综合结果能够被重复利用，因此如果按照多分辨的高低方向实现可视化，可视化时间明显减少。从表2中同一比例尺下对比三种索引方法的时空性能发现，在处理时空复杂性上明显优于另外两种索引方法。

3.3 结果对比分析

针对某露天矿采场区域的开采变化过程，对比例尺为1 ∶200 000至1 ∶400 000的运输道路的多维、多分辨率时空数据显示结果进行实验比较，如图7所示。该实验过程中的数据是以该露天矿采场不同尺度的运输道路地图为基础，通过使用Brinkhoff时空数据生成器生成相同对象(道路网)数目，形成不同尺度下的数据集，然后使用4DHMSR树的索引创建算法和节点选择子算法等对不同尺度数据集中的海量路网数据进行组织和管理，最后将相同时间点内的不同运输道路对象数据进行索引和查询，采用可视化工具对索引到的有效数据进行区域建模。

(a) 1 ∶200 000显示结果

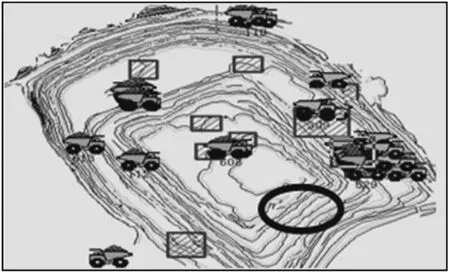
(b) 1 ∶250 000显示结果

(c) 1 ∶300 000显示结果

(d) 1 ∶400 000显示结果图7 4DHMSR树的多维、多分辨率显示结果

从图7的显示效果可知，特别是圈定的运输道路部分区域，可以清晰地发现，由于受到部分采场图形区域分辨率的制约，图7(a)与图7(b)的比例尺变化程度相对较小，但图7(a)中部分道路区域的显示分辨率要远远高于图7(b)，从图7(c)到图7(d)的渐变过程发生明显变化，这些随比例尺变化过程是多维、多分辨率时空数据表达过程，充分可以证明4DHMSR树完全支持时空数据的多维、多分辨率表达方法。

为了进一步验证本文索引方法与文献[24]研究结果的差异性，将4DMHSR树与Octree从存储空间与计算时间两个方面分别进行了对比，如图8-图9所示。两者的主要区别是：(1) 4DHMSR树的索引方法是以4D十六叉树存储结构为基础，4DHMSR树中的节点分裂过程中产生的时间复杂度为O(N)，而MSR树与Octree树的时间复杂度为O(N2)。(2) 4DHMSR树能够充分表达多分辨率和多尺度的时空数据；而文献[25]索引方法只是建立在传统的R树基础上，只能表达单分辨率的空间数据。(3) 4DHMSR树的内外存储子索引分别是4D十六叉树和MSR树，从而可以较好地索引时空数据，无需额外的时间存储开销；而文献[25]提出的索引树结构的内外存子索引结构分别采用Hash表和R树、B树，在索引时空数据时，特别是时间属性的表达时，需要额外的内外存开销。

图8 计算时间的比较

图9 占用的存储空间

从图8可知，随着地理空间对象尺度的增加，三维八叉树索引的计算时间明显增加，但4DHMSR树索引的计算时间趋于平稳状态，这表明4DHMSR树结构凭借十六叉树结构的时空对象分裂和位置定位，可快速索引到目标对象在树形结构中的位置，从而减少了目标对象的索引计算时间。

从图9可知，随着地理空间尺度和计算时间的增加，三维八叉树结构占用的存储空间要比4DHMSR树所占用的存储空间少，这是因为四维十六叉树结构在给定的分辨率或阈值下，需要对索引的目标对象所在的区域进行递归分裂为不同的子立方体，而这个分裂过程需要占用大量的外存和缓存空间，由此导致4DHMSR树结构占用较多的存储空间，这需要构建符合多维、多分辨率和多尺度时空数据索引的删除和更新算法，实现索引过程中新旧对象的实时清理和更新。

4 结 语

虽然目前国内外对R树、改进的R树数据结构的研究成果较为丰富，但主要是以空间对象数据检索和八叉树数据结构为主，但在十六叉树结构与多尺度表达的R树集成方法中增加时间维度和多分辨率维度，可弥补消耗时间长的不足。由于十六叉树数据结构在表达四维时空对象占用的空间相对较大，但在处理速度上却比八叉树结构要快。同时，为了快速创建索引结构和选择有效的目标节点，设计了4DHMSR树的动态插入和分裂算法，加速索引目标数据的选择和插入操作。

本文从理论上对十六叉树与多尺度表达R树集成的数据结构(4DHMSR树)进行了探讨，将具体的工程实例在计算机上进行了实验和分析，包括4DHMSR树的时空性能和可视化，使得十六叉树与R树理论探索与实际应用向前迈进一步。为了进一步提升十六叉树结构的性能，设计出符合4DHMSR树的记录更新和删除算法将是本文下一步研究的方向。