基于GWO-BP神经网络的电池SOC预测方法研究

鲍 伟 任 超

(合肥工业大学电气与自动化工程学院 安徽 合肥 230009) (工业自动化安徽省工程技术研究中心 安徽 合肥 230009)

0 引 言

随着电动汽车的不断发展，对电动汽车的性能和安全性等的要求越来越高，对动力电池系统状态的准确估计就显得尤为重要。锂离子电池的荷电状态(State of charge)反映了电池的剩余容量占额定容量的百分比。准确地估算电池SOC对于保证电池性能，提高使用安全性，延长使用寿命具有重要意义[1]。

近年来估算电池SOC的主要方法有：卡尔曼滤波法、开路电压法、安时积分法、神经网络法等[2]，但是它们都有各自的适用条件。卡尔曼滤波法涉及到模型中各个参数的辨识与复杂方程的解析问题，增加了模型的复杂度；开路电压法需要预计开路电压，不适用于运行中的电池SOC估算；安时积分法在一定程度上忽视了电池自放电率、老化程度和充放电倍率对电池SOC的影响，长期使用也会导致测量误差不断累积扩大。由于电池本身是一个高度非线性的复杂系统，要想建立准确的数学模型来描述电池的充放电过程难度很大，而神经网络具有非线性和自学习的特点，在给出外部激励的情况下，能够较好地模拟电池的非线性特性，从而对SOC进行有效的估算[3]，但是传统BP神经也存在着受初始权值和阈值影响较大、预测精度不高的问题。

同时随着云平台技术的发展，越来越多的电动汽车将电池的数据上传到云平台上。如果利用上传的这些数据对电池SOC进行预测，将预测的值和由电池管理系统上传到云平台的SOC值相互验证，对于优化SOC预测算法和电池管理系统的故障诊断都具有重要意义。本文通过深入分析上传到云平台上电池数据库中的采样数据，结合灰狼算法优化的BP神经网络(GWO-BP)，提出了基于GWO-BP神经网络的电池SOC预测方法。灰狼优化算法强大的全局搜索能力克服了传统BP神经网络收敛速度慢，过度依赖初始权值和阈值的缺点[4]。实验结果表明，该方法具有较高的预测准确率。

1 BP神经网络

BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，它具有对内部复杂的问题具有较好的适应性。但同时，它是一种局部搜索算法，容易陷入局部极值[5]。

神经网络由输入层、隐含层和输出层组成。三层网络的基本结构如图1所示。

图1 BP神经网络结构

定义图1中输入层、隐含层、输出层节点数分别为l、m、n。i、j、k分别代表输入层、隐含层和输出层第i、j、k个神经元。隐含层的激活函数采用sigmoid函数。

输入层到隐含层的权值矩阵为W1，阈值矩阵为B1，隐含层到输出层权值矩阵为W2,阈值矩阵为B2，输入向量为X，输出向量为Y,期望输出向量为O，隐含层输出值向量为V,隐含层误差值向量为U1，输出层误差值矩阵为U2。各定义矩阵和向量形式如下：

1) 正向传播。正向传播的矩阵形式为：

f(W1X+B1)=V

W2V+B2=Y

式中：f表示隐含层的激活函数。

2) 反向传播。定义目标函数如下：

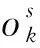
反向传播的矩阵形式为：

U2=O-Y

(W2)TU2∘V∘(1-V)=U1

W1←W1+ηU1XT

W2←W2+ηU2VT

B1←B1+ηU1

B2←B2+ηU2

以上就是单样本输入时BP神经网络的矩阵形式。

2 数据集简介与数据预处理

2.1 数据集简介

本文的数据集来源于某电动汽车公司云平台的数据库。数据集由BMS实时采集和上传的动力电池运行过程的各项参数构成。电池数据库中的数据有数据上传时间、电池系统SOC、电流(A)、电池单体平均电压(mV)、电池单体最大电压(mV)、电池单体最小电压(mV)、电池包平均温度(℃)、电池包最大温度(℃)、电池包最小温度(℃)、电池包总电压(V)等，其中采样时间间隔为10 s。

2.2 变量的选择与数据预处理

SOC值的变化与电池的总电压，电流等相关，又因为环境温度的变化会影响电池内部化学反应的快慢，从而影响SOC的变化，所以电池的温度也是一个影响因素。因此实验选择了与SOC关联较大的当前时刻的电池包总电压、电流、电池包平均温度作为输入变量，电池包的SOC作为输出变量[6]。

为了消除指标间的量纲和奇异样本数据的影响，要对输入数据和输出数据归一化[7]。分别将输入矩阵和输出向量进行行归一化到[-1，1]，采用式(1)的归一化方法：

(1)

式中：vstd表示归一化后的值；v表示原始值；vmin表示变量v所在行的最小值；vmax表示变量v所在行的最大值。

输入变量是电压、电流和平均温度三个变量，输出变量为电池SOC。对于训练过程来说，输入是电压、电流、平均温度组成的3×M的矩阵，形式如下：

(2)

式中：M表示训练集样本总数。输出是电池SOC组成的1×M的一个行向量，形式如下：

(3)

2.3 训练样本和神经网络模型的分类

由于电动汽车在放电过程和充电过程中，电池包电流的特点不一样。放电过程中，电流根据驾驶员意图和工况随机变化。而充电过程中电流在长时间内保持恒定值。因此根据电流的特点，将训练数据和SOC神经网络预测模型分成充电模型和放电模型分别进行训练和建模，则能够取得更好的效果。

3 基于GWO-BP神经网络的电池SOC预测

3.1 灰狼优化算法

灰狼优化算法(Grey Wolf Optimizer，GWO)是由澳大利亚格里菲斯大学学者Mirjalili等[8]于2014年提出来的一种群智能优化算法。该算法受到了灰狼捕食猎物活动的启发而开发的一种优化搜索方法，是一种元启发式算法。它具有全局搜索能力强、较强的收敛性能、参数少、易实现等特点。Mirjalili通过一系列标准测试函数验证了GWO比PSO、GA、DE算法等收敛速度快，稳定性更强[9]。

灰狼隶属于群居生活的犬科动物，且处于食物链的顶层。灰狼严格遵守着一个社会支配等级关系。按照等级划分，灰狼可以分为四个等级，由高到低分别是α、β、δ、ω。围捕猎物包含三个过程，分别是搜索猎物、围捕和包围猎物、攻击猎物[10]。

在数学上模拟包围猎物的过程可以用式(4)-式(7)来表示[11]：

A=2ar1-a

(4)

C=2r2

(5)

D=|CXp(t)-X(t)|

(6)

X(t+1)=Xp(t)-AD

(7)

式中：t表示迭代次数；Xp(t)表示猎物的位置矢量；X(t)表示t代灰狼的位置矢量；X(t+1)表示t+1代灰狼的位置矢量。a在迭代过程中随着迭代次数线性地由2减小到0，可用式(8)来表示。

(8)

式中：l代表当前迭代次数；Max_iteration表示最大迭代次数。r1和r2是[0,1]中的随机数。

在每只灰狼更新结束后，计算每一只灰狼的适应度值，选出适应度值最小的三个解Xα(t)、Xβ(t)、Xδ(t)作为当前α、β、δ的位置，下一代灰狼以α、β、δ为牵引，通过式(9)-式(12)更新个体的位置[12]：

Xα(t+1)=Xα(t)-A1|C1Xα(t)-X(t)|

(9)

Xβ(t+1)=Xβ(t)-A2|C2Xβ(t)-X(t)|

(10)

Xδ(t+1)=Xδ(t)-A3|C3Xδ(t)-X(t)|

(11)

(12)

由式(4)可知A的取值范围为[-a,a]，当|A|<1的时候，灰狼朝着猎物发起进攻，灰狼的攻击行为使得灰狼算法有良好的局部搜索能力；当|A|>1的时候，灰狼远离猎物去寻找下一个更合适的猎物，这也使得算法有较好的全局搜索能力[13]。

3.2 基于GWO-BP的电池SOC预测算法

定义灰狼算法中的两个参数N和R。其中，N代表灰狼种群规模；R代表搜索空间维度。每只灰狼的维度就是其位置向量，它们代表BP神经网络的权值和阈值。

BP神经网络输入层节点、隐含层节点、输出层节点分别设为l、m、n，搜索空间维度R的计算过程如下：

R=m×l+n×m+m+n

(13)

为了方便计算，对于种群N，将维度分成四部分，分别是W1、B1、W2、B2。对于W1，初始化一个Nm×l的矩阵，则矩阵的第im-m+1行到第im行为第i只灰狼输入层到隐含层的权值矩阵。其他权值矩阵和阈值矩阵定义方式和上述方法一样。构造适应度函数如下：

(14)

基于灰狼算法的BP神经网络预测电池SOC步骤如下：

(1) 首先对输入矩阵和输出向量归一化，将输入矩阵和输出向量的每一行归一化到[-1，1]。

(2) 设置BP神经网络的最大迭代次数Max_epochs、学习率η、目标误差Target_error。

(3) 初始的维度代表BP神经网络初始的权值和阈值，将初始的维度均初始化到[-1，1]，然后代入BP神经网络进行训练，根据式(14)计算出每只灰狼的适应度值并且从小到大排序，选出第一代适应度值最小的3只灰狼，它们在原来种群中的序号分别记为α、β、δ。

(4) 根据式(9)-式(12)更新每只灰狼个体的位置，构造新的BP神经网络并进行训练，计算出每只灰狼的适应度函数值，选出新的α、β、δ，再对每只灰狼的位置更新。

(5) 判断是否达到GWO最大迭代的次数Max_iteration，若没有达到，返回步骤(3)，若达到，记录最优灰狼个体α对应的BP神经网络的初始权值和阈值。

(6) 根据得出的优化过的初始权值和阈值，代入BP神经网络训练，当训练误差满足要求时，停止对网络的训练。

(7) 将测试集代入训练好的BP神经网络，得出SOC。

基于GWO-BP神经网络预测电池SOC流程如图2所示。

图2 GWO-BP预测电池SOC流程

4 实验结果及分析

为了对比灰狼优化算法和其他优化算法优化BP神经网络的效果，采用一种粒子群优化算法优化BP神经网络进行对比验证。粒子群优化算法同灰狼优化算法一样，都是一种基于群体智能的进化计算方法，在计算一些连续函数的优化问题具有比较好的效果[14]。

选取相同的10 000组云平台数据分别训练BP、GWO-BP和PSO-BP神经网络模型，其中放电过程和充电过程分别为5 000组。实验相关参数设置如下：

BP：输入和输出节点分别为3和1，由经验公式m=2l+1可得隐含层节点数为7，最大迭代次数Max_epochs设为5 000，学习率η设为1×10-4，目标误差Target_error设为0.001。

GWO-BP：灰狼种群数N设为30，搜索空间维度R为36，GWO最大迭代次数Max_iteration设为50。其余参数设置与BP神经网络一样。

PSO-BP：粒子群规模particlesize设为30，粒子最大迭代次数Max_num设为50，相关的系数c1=2，c2=2，ω=0.6，粒子的最大速度vmax=0.8，每个粒子的维度dims=36，其余参数设置与BP神经网络一样。

4.1 GWO-BP预测结果及分析

根据以上训练数据集和算法的参数设置，最终得到GWO-BP神经网络权值和阈值如下：

放电过程：

B2=0.529 7

充电过程：

B2=-0.953 7

最终放电过程的种群序号为α=6，β=18，δ=4；充电过程的种群序号为α=15，β=24，δ=6。再选取2 503组云平台数据作为测试样本，其中放电过程1 072组，充电过程1 431组测试GWO-BP神经网络预测动力电池SOC的准确性。SOC预测效果及误差曲线如图3至图6所示。

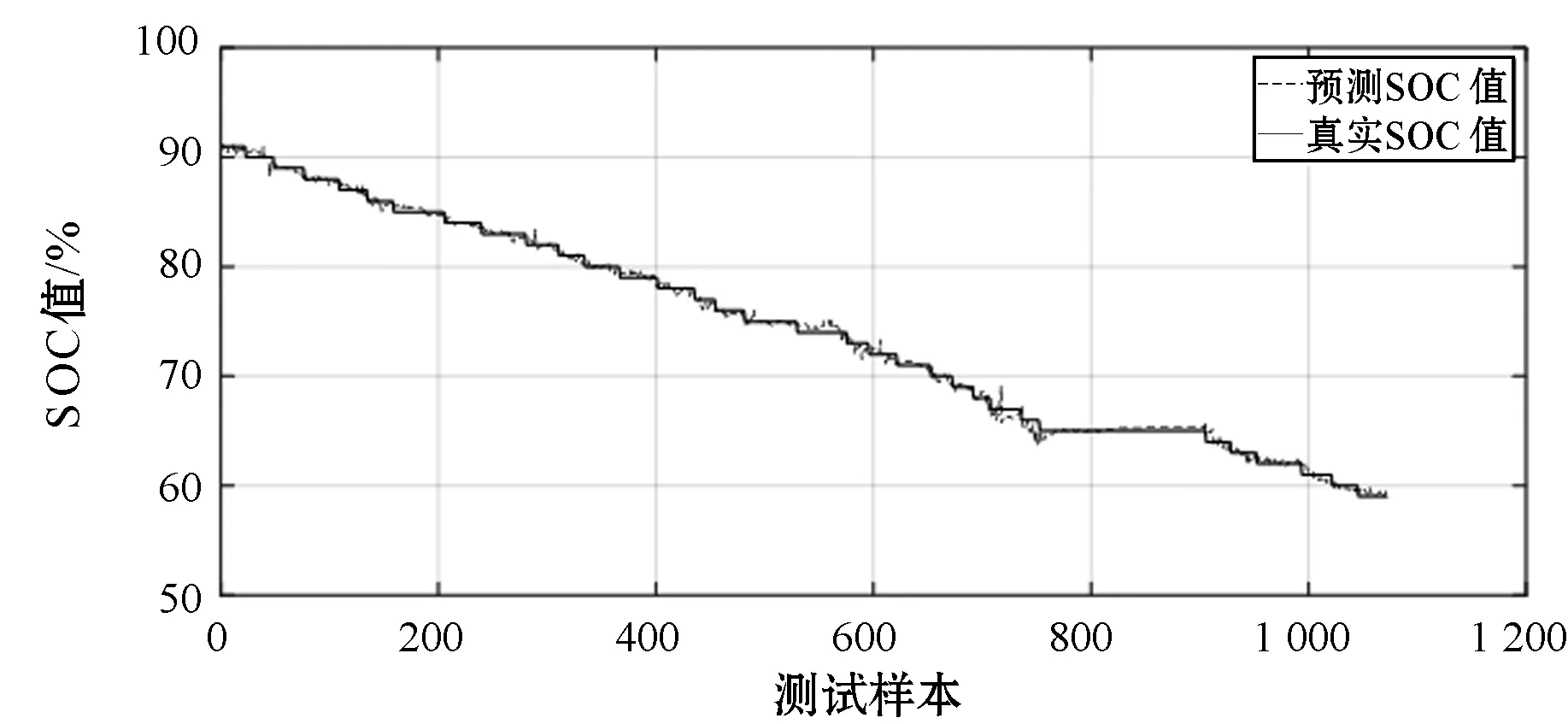
图3 放过程GWO-BP测试样本SOC值对比

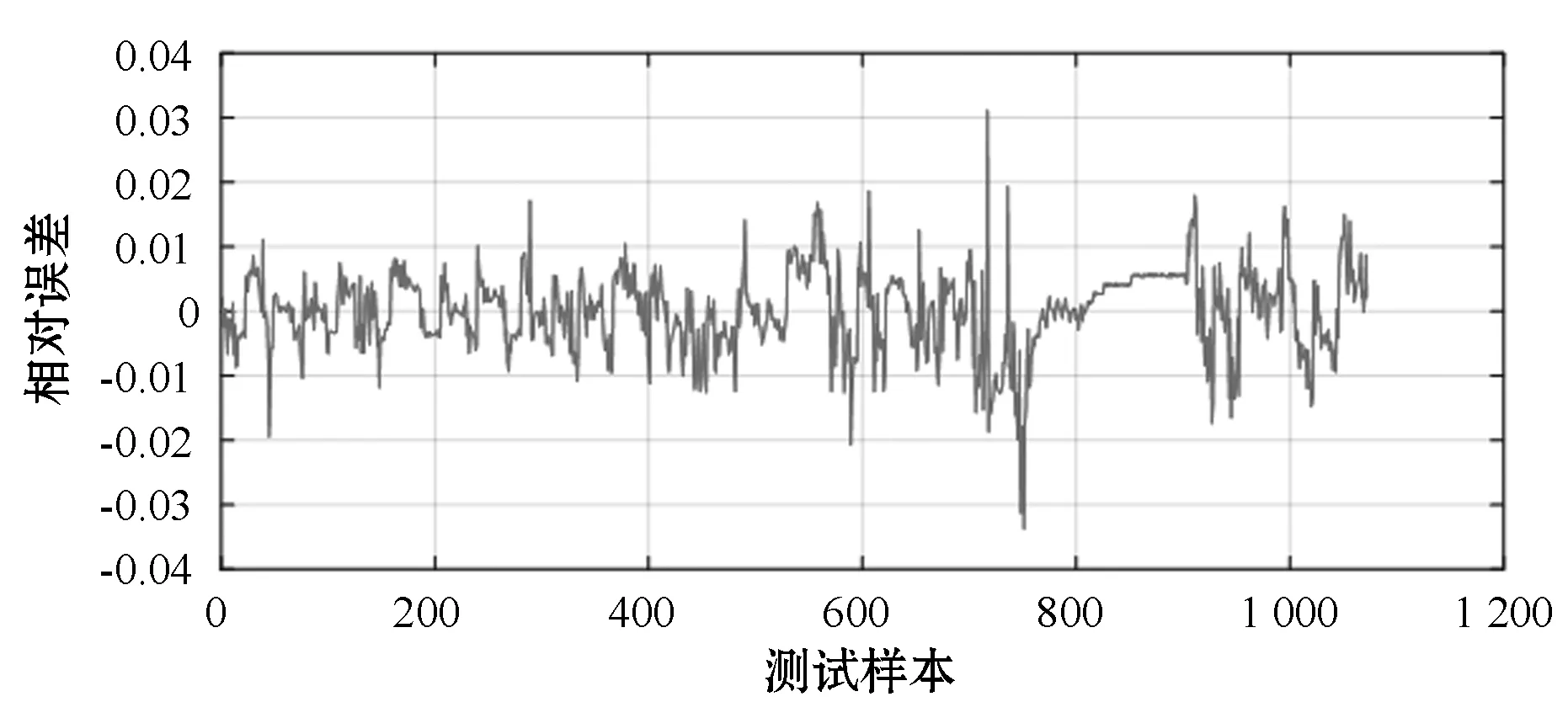
图4 放电过程GWO-BP测试样本相对误差

图5 充电过程GWO-BP测试样本SOC值对比

图6 充电过程GWO-BP测试样本相对误差

从图4和图6可以看出，放电过程平均相对误差为0.48%，最大相对误差为3.42%。充电过程平均相对误差为0.34%，最大相对误差为1.12%。预测SOC值和真实SOC值也基本吻合。

4.2 BP神经网络预测结果及分析

根据以上训练数据集和算法的参数设置，获得基于BP神经网络的SOC预测值，相关的预测效果和误差曲线如图7至图10所示。

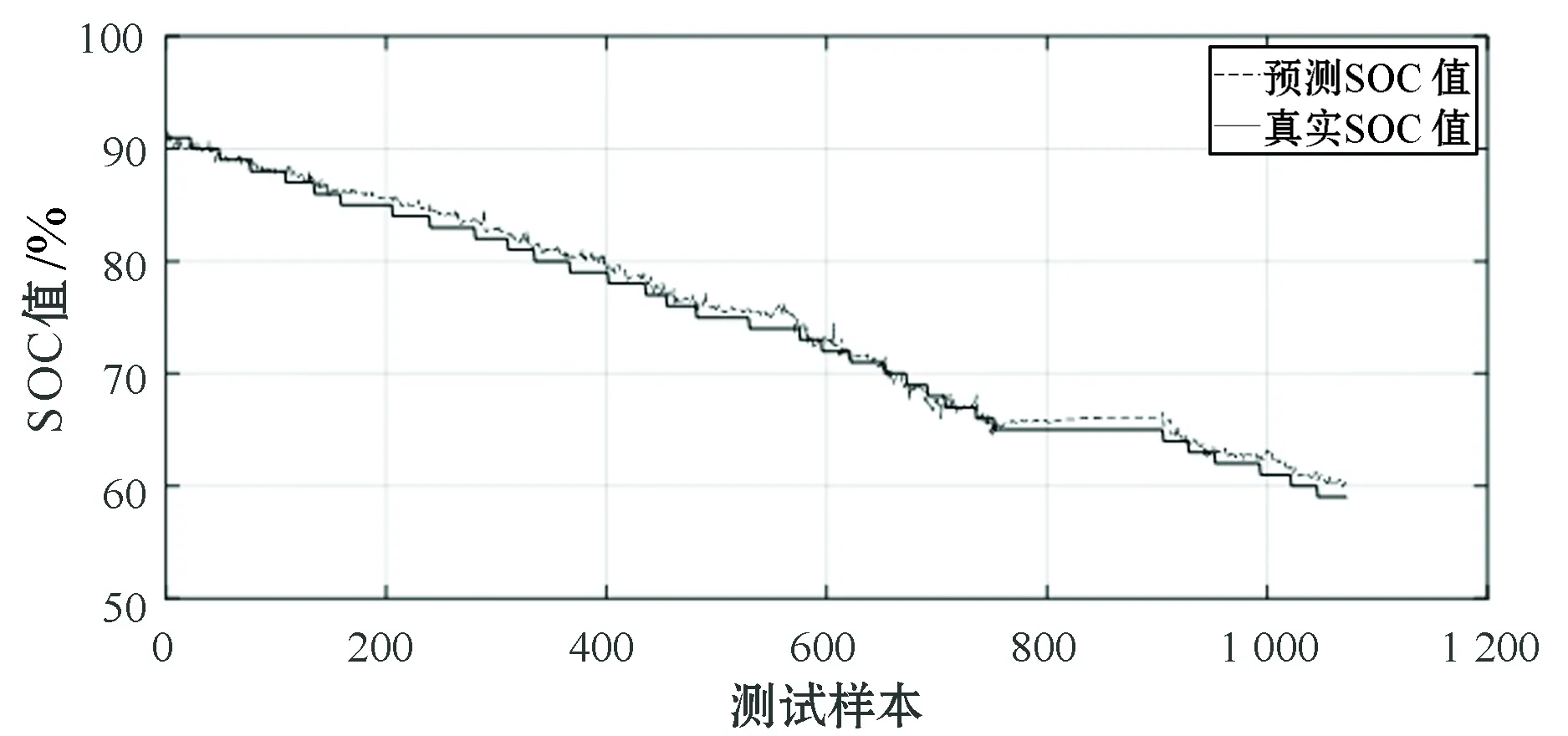
图7 放电过程BP测试样本SOC值对比

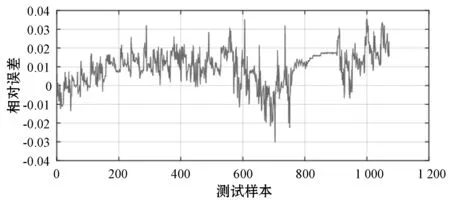
图8 放电过程BP测试样本相对误差

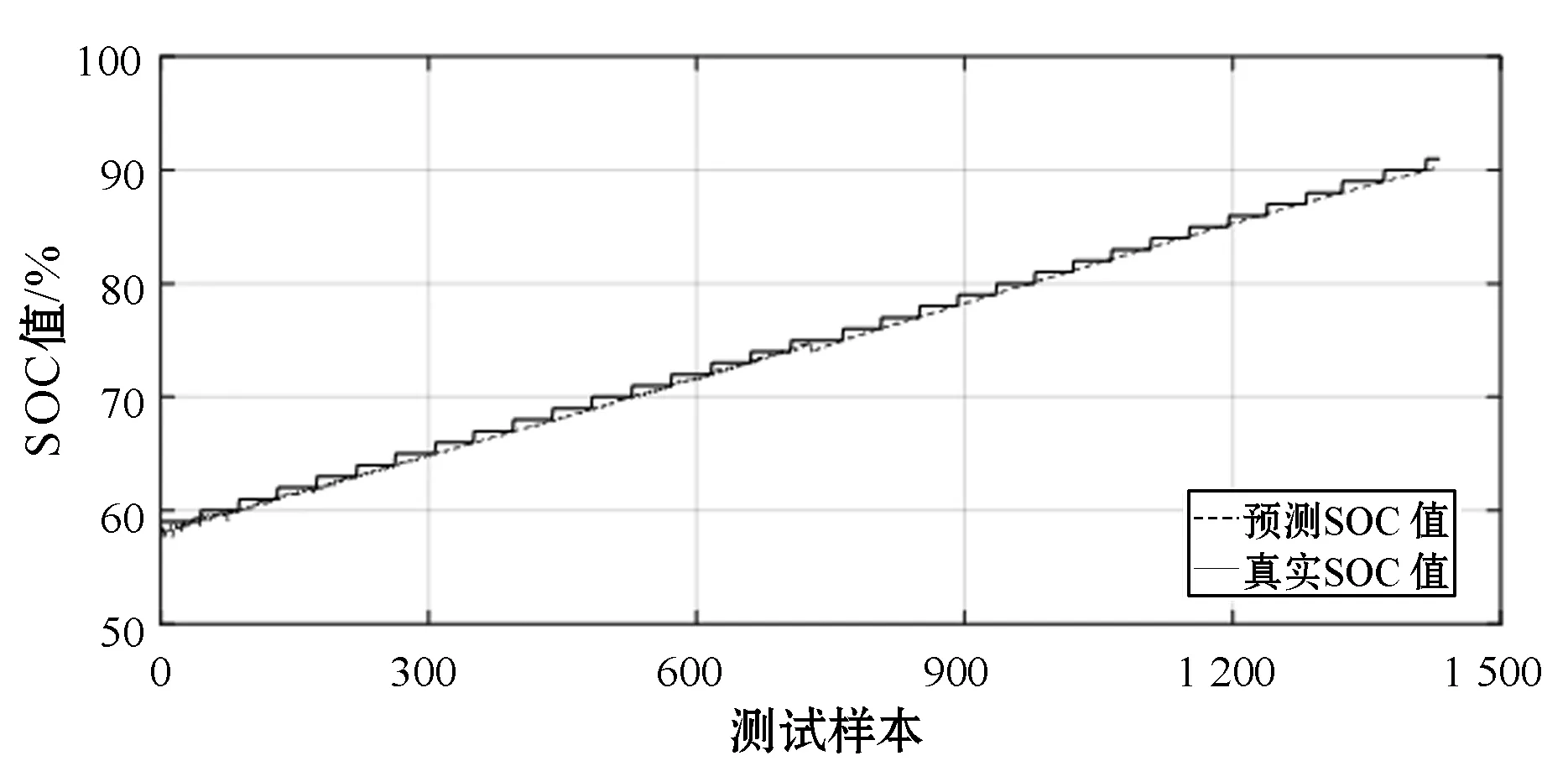
图9 充电过程BP测试样本SOC值对比

图10 充电过程BP测试样本相对误差

从图8和图10可以看出，基于BP神经网络的SOC预测结果，放电过程SOC预测的平均相对误为1.13%，最大相对误差为3.77%；充电过程SOC预测的平均相对误差为0.63%，最大相对误差为2.64%。

从上述实验结果可以看出，无论是充电过程还是放电过程，基于GWO-BP神经网络的SOC预测准确度要优于BP神经网络。

4.3 PSO-BP神经网络预测结果及分析

根据同样的训练数据集和测试数据集以及PSO优化算法的参数设置，预测效果如图11至图14所示。

图11 放电过程PSO-BP测试样本SOC值对比

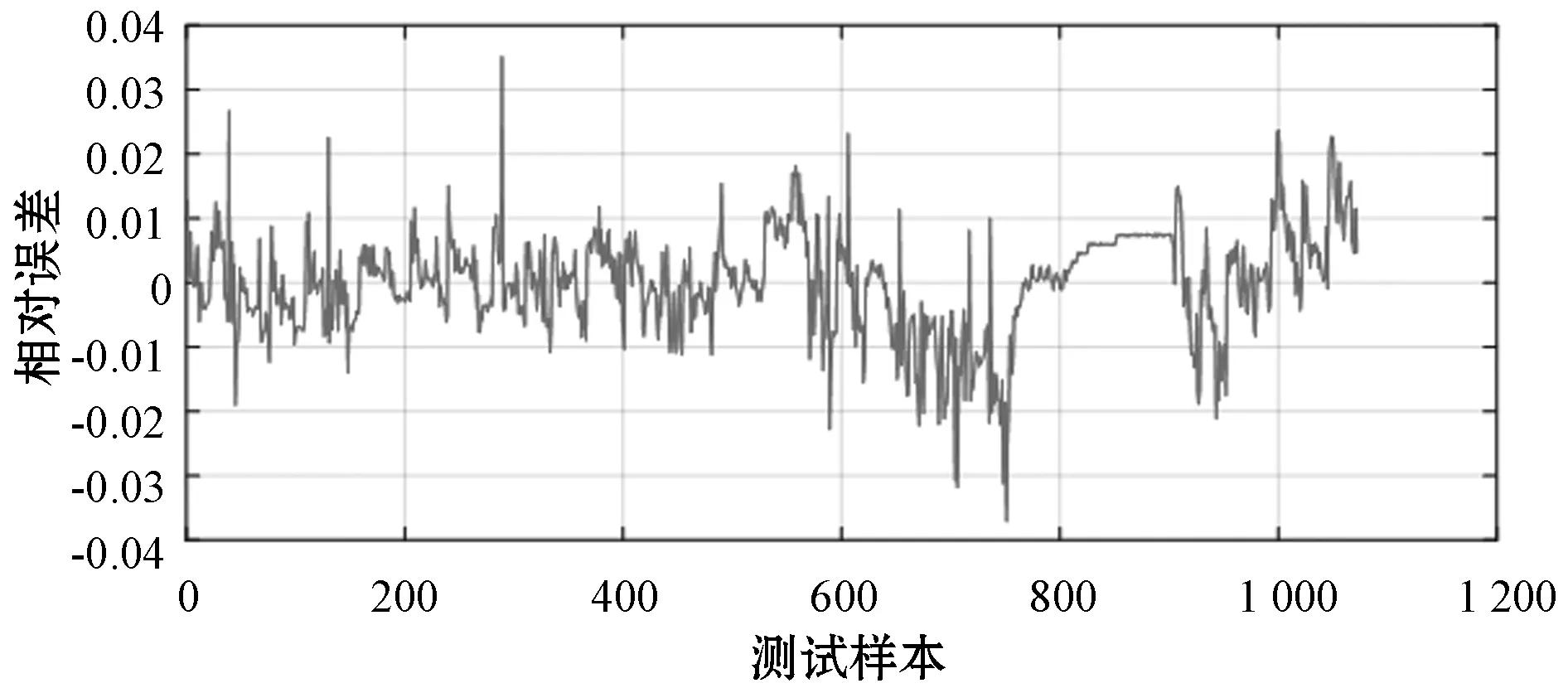
图12 放电过程PSO-BP测试样本相对误差

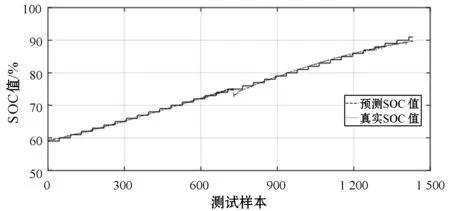
图13 充电过程PSO-BP测试样本SOC值对比

图14 充电过程PSO-BP测试样本相对误差

从图12和图14可以看出，基于PSO-BP神经网络的SOC预测结果，放电过程SOC预测的平均相对误为0.59%，最大相对误差为3.86%；充电过程SOC预测的平均相对误差为0.53%，最大相对误差为3.21%。

4.4 GWO-BP、BP、PSO-BP神经网络的预测结果对比与分析

三种神经网络充放电误差对比如表1所示。

表1 三种算法充放电过程误差对比(%)

三种算法充放电过程训练预测时间以及占用内存如表2所示。

表2 三种算法充放电过程训练时间及占用内存对比

由表1可以看出充电过程和放电过程中，GWO-BP神经网络的平均相对误差比未优化的BP神经网络和PSO-BP神经网络都要小。由此可见，经过灰狼算法优化过的BP神经网络比粒子群优化的BP神经网络在优化BP神经网络的初始权值和阈值方面效果更好，进一步提升了预测准确率。由表2可以看出PSO-BP和GWO-BP不管是在充电过程还是放电过程，其训练预测时间和占用内存都很接近，而BP神经网络相对于两种优化过的算法，其训练预测时间较短，占用内存较小。

5 结 语

本文基于电动汽车云平台长采样周期的电池运行数据，进行电池SOC预测算法的研究。特别是考虑到电动汽车的特点，将SOC神经网络预测模型分成充电模型和放电模型分别进行训练和建模，得到了较为理想的结果。

本文利用GWO算法优化BP神经网络的权值和阈值，解决了BP神经网络依赖初始权值和阈值的问题，进一步提高了神经网络SOC预测算法的精度。实验结果表明，无论是充电过程还是放电过程，GWO-BP神经网络比未优化的BP神经网络和PSO-BP神经网络预测精度更高。

随着未来5G通信技术的发展和普及，流量和通信速度会极大提升，上传到云平台的电池运行数据的采样周期会极大地缩短，更多的细节部分会保留下来，则通过云平台直接计算SOC并反馈给BMS将会成为可能，SOC估计的精度将会有着极大的提升。