常数变易法的思想探究及其在低阶变系数非齐次微分方程中的应用
王艳华 潘志刚
1.成都锦城学院 四川成都 611731;2.西南交通大学数学学院 四川成都 611756
1 概述
常数变易法是求解非齐次线性微分方程的一种行之有效的方法,它是Joseph-Louis Lagrange近十一年的研究成果,目前大学教材沿用的仅是该方法的结论,只有具体求解步骤而没有解释缘由,这使得初学者对其逻辑不甚清晰,加之限于学时等原因,课堂上少有涉及。基于此,本文将尝试对常数变易法的思想本质进行深入探究,并将其应用在低阶变系数非齐次微分方程的求解中。
2 常数变易法思想探究
′+()=()
(1)
定义形如上式(1)的方程称为一阶非齐次线性微分方程,()、()是关于的连续函数。
当()=0时,式(1)变为:
′+()=0
(2)
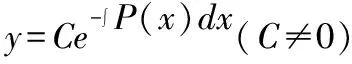
此时采用常数变易法,将式(2)解中的常数变易为的未知函数(),令:
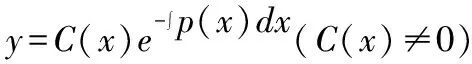
(3)

将其代入式(3),即可得到非齐次常微分方程(1)的通解为:

(4)
这就是本科阶段专业课“常微分方程”里的经典求解步骤,但老师们在课堂上往往只会介绍到这里,而没有更多的时间与精力带着学生探究其原理,学生也只会套用这个过程,而不明白其原理,更不知道是否正确,所以我们很有必要对此一探究竟。常数变易法思想的具体过程探究如下:


但当式(1)中()≠0时,
=[()-()]
(5)
思考一:此时式(5)无法分离变量。
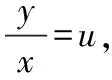
即

(6)
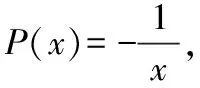
思考三:结合思考二的结论可以换一种思路,利用构造函数的方法,将任意函数()表示为两个函数之积,令:
()=()·()
(7)
将其代入(1),整理得:
′()·()+()·[′()+()·()]=()
(8)
此时想利用分离变量法解决问题,只能令′()+()()≡0。

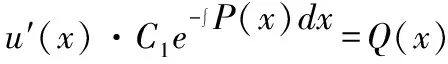
分离变量后左右两边积分得:

(9)
故
()=()·()
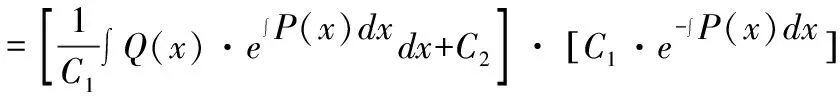

(10)
即式(1)的通解为:

由此可见,将分解为两个函数的积,在实际的求解中是将一个不能直接用分离变量法的微分方程化成了与之对应等价的两个可以直接应用分离变量法的微分方程。
通过进一步观察可以发现,()的解恰好是求解非齐次线性常微分方程′+()=()对应的齐次线性常微分方程′+()=0。这正好解释了教材中的求解技巧:在求解非其次线性常微分方程时,首先要求解对应的齐次微分方程,得到其通解:
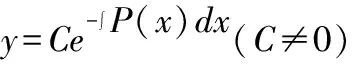
(11)
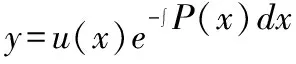
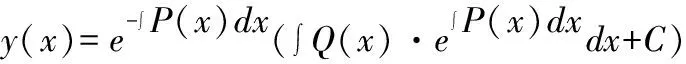
3 常数变易法在求解一阶非齐次线性常微分方程中的应用
对于一阶非齐次线性微分方程,教材中的解题步骤已在前面给出,只须按照步骤一一准确计算即可。
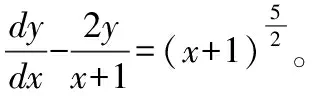

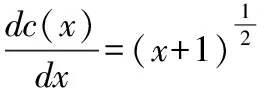

所以非齐次线性微分方程的通解为:

4 常数变易法在求解二阶变系数非齐次线性常微分方程中的应用
对于二阶常系数非齐次线性微分方程,教材中的做法是:首先,利用对应的特征方程求出特征根,根据特征根得到对应齐次微分方程的通解;其次,根据非齐次项的特点,设出相应的微分方程特解形式;最后,利用待定系数法将所设出的特解代入原方程,求出非齐次线性微分方程的通解。胡劲松先将二阶变系数方程转化为Riccati方程后予以求解;孙智勇结合Maple软件讨论了一类二阶变系数微分方程的求解,更多关于二阶变系数的求解技巧可参见文献。
对于求解二阶变系数非齐次线性微分方程,常数变易法最为简便。由于非齐次微分方程的通解是对应齐次微分方程通解加一个特解的形式,所以接下来先讨论二阶变系数齐次线性常微分方程的求解。
″+()′+()=()
(12)
定义形如上式(12)的方程称为二阶变系数非齐次线性微分方程,其中()、()是关于的连续函数。
定理1 若()是二阶变系数非齐次线性微分方程(12)对应的齐次方程(13)的一个已知特解,则如下结论成立:
①=()也是方程(13)的一个解;

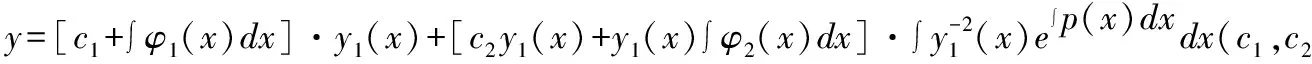
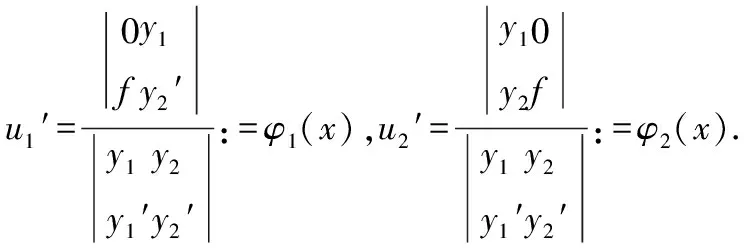
证明 第一步:设方程(12)对应的二阶变系数齐次线性微分方程的一个解为(),则()也是(13)的一个解。
″+()′+()=0
(13)
利用常数变易法,令()=()(),且()、()线性无关。
第二步:将()代入齐次方程(13)得
()[″()+()′()+()()()+()′()+()()]+″()()+2′()′()+()′()()=0
由于()是方程的一个特解,则:
″()+()′()+()()=0
所以上式可简化为:
[2′()+()()]′()+″()()=0
(14)
第三步:令()=′(),则式(14)可以表示为:
[2′()+()()]()+′()()=0
此时式(14)降阶成为一个一阶齐次线性微分方程。
第四步:利用分离变量法求解一阶齐次微分方程得:



第五步:写出二阶变系数齐次线性微分方程(13)的通解。

对于二阶变系数线性非齐次微分方程(12)的通解,接下来只需要找到其特解即可。
设=+是方程(12)的一个特解。
将其代入式(12):




所以

(+)()=()
又因为、是对应齐次方程(13)的解,则
″+()′+()=0″+()′+()=0
从而:
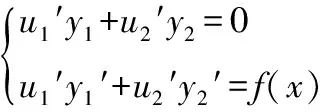
(15)
方程组(15)系数行列式不为零,故有唯一解:
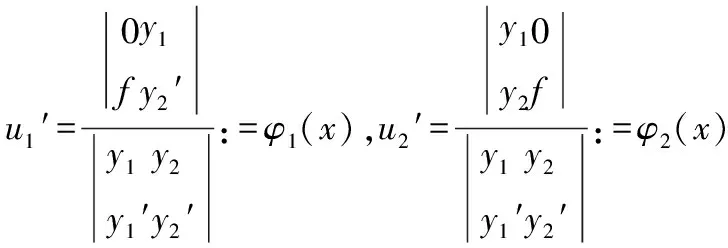
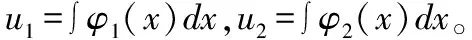
综上二阶变系数非齐次线性方程(12)的通解为:

例:已知齐次方程(-1)″-′+=0的通解为()=+,求非齐次方程(-1)″-′+=(-1)的通解。
解:将所给方程写成标准形式
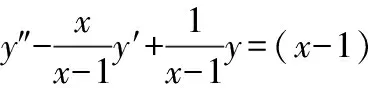
令=+,则=,=。
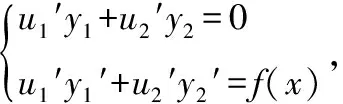
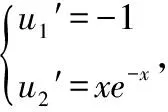
所以非齐次方程有特解=-(++1),从而所求非齐次方程的通解为=+-(++1)。
结语
本文基于“常数变易法”的求解步骤,利用分离变量的思想,探讨得到了该方法的思想本质是齐次化原理,通过将原非齐次方程进行特殊的变量代换得到两个等价的齐次方程,而且第一个齐次方程的结构恰好就是原非齐次方程对应的齐次方程,这正好解释了“常数变易法”里第一步就是为什么要直接求解对应齐次方程的通解。接着运用该特殊变量代换方法到低阶的变系数非齐次方程的求解,该方法对于二阶变系数非齐次方程的求解是一个有益的补充与扩展。

