Abnormal enhancement to the quality factors of carbon nanotube via defects engineering

Ke Duan,Li Li,Sihan Liu,Yujin Hu,Xuelin Wang

State Key Lab of Digital Manufacturing Equipment and Technology,School of Mechanical Science and Engineering,Huazhong University of Science and Technology,Wuhan,430074,China

Keywords:Defects engineering CNT resonator Q factor

ABSTRACT Low quality (Q) factor is often the limiting factor for high performance carbon nanotube (CNT) resonators.The most commonly used approach to enhance the Q factor of CNTs is to reduce/eliminate the intrinsic defects.Herein,we show surprisingly that hole defects of suitable size and position are able to enhance the Q factor of CNT,which strongly contradicts to the common notion that the presence of defects promote intrinsic dissipation via defects dissipation.By analyzing the strain distribution,we find that such abnormal enhancement in Q factor of defected CNT originates from a coupling competition mechanism between the atomic mismatch around defected atoms and the thermoelastic damping.Although the presence of holes will introduce an additional defect dissipation source,suitable holes are capable of reducing the energy dissipation arisen from the thermoelastic damping,through changing the spatial strain field of defected CNT.This coupling competition mechanism provides a new route for designing high performance CNT resonators via defects engineering.

1.Introduction

Over the past few decades,rapid advances in nanoresonators have led to dramatic progress at the frontiers of modern physics and nanotechnology,such as nanoscale actuation and sensitive detection of molecular mass [1–6].To date,the design and fabrication of nanoresonator with higher sensing performance are ongoing pursuits in the scientific communities.Essentially,lower mass combined with higher quality factorQare two critical features to offer extraordinary sensing capability of a nanoresonator[7].Therefore,researchers have devoted extensive efforts in developing nanoresonators using materials of extremely small mass/size,or improving theQfactors of a specific material/structure based on a variety of strategies such as the phononic engineering[7],the strain engineering[8–10],and the removal of internal or surface defects[11].

Among all those materials used for nanoresonators,carbon nanotubes(CNTs)have long been regarded as one of the most ideal candidates due to their minuscule mass,high resonant frequency,and relatively highQfactors [3,12–15].Some reports have already demonstrated the unprecedented level of sensitivity of CNTs,which have a resolution of several yg(1 yg ＝10-24g),allowing for the detection of single napththalene molecule [2,16].However,the stable use of high sensitive CNT nanoresonators in industrial and scientific communities is far from mature,due to the reason that CNTs grown by the most used chemical vapour deposition (CVD) approach generally suffer from structural deviations and unavoidable occurrence of structural defects,such as single vacancy(SV),double vacancy (DV),and hole defects [17,18].In particular,for nanoresonators operated at vacuum,structural defects usually lead to a lowQfactor that is much below the ideal limit arisen from intrinsic dissipation mechanisms such as thermoelastic damping (TED) and Akhiezer mechanism[14,19].For nanomaterials consisting of one or few atomic layers,such as CNTs or graphenes,structural defects may have more pronounced impact on the sensing performance by lowering theirQfactors.For instance,Kim et al.found that theQfactors of graphene based resonators drop significantly due to the presence of single vacancies even at a low concentration of 1% [20].Also,grain boundaries in the CVD-grown poly-crystalline graphene will lead to lowerQfactors that are 1–2 orders of magnitude smaller than that of perfect mono-layer graphene[21].

Although structural defects play a critical role in affecting theQfactors of CNT based nanoresonators,research on this topic is,however,very limited,and the underlying mechanisms at play remain unclear.In fact,the abundant defect types that can be introduced to the CNT surface may provide new route for the design of property-tunable CNT based devices,namely the defect engineering [22].For instance,Wang et al.showed that the Young's modulus,tensile strength,and theQfactor of the CNTs can be controllably,reversibly,and repeatedly tuned via defect engineering technique,which was achieved by a highly controllable defect handling approach,i.e.,defect creation by the use of electron irradiation and defect elimination through current-induced annealing[22,23].

Inspired by the high precision defect handling techniques [22–24],herein,we investigate the effects of various defect types on the dissipation characteristics of CNT using molecular dynamics(MD)simulations,in order to not only provide some insights into the dissipation mechanisms but also explore the possibility of improvingQfactors of defected CNTs via defect engineering.Surprisingly,we find that the presence of hole defects with suitable size and position is able to enhance theQfactors of defected CNTs,which strongly contradict to the common notion that crystal defects promote dissipation and reduce theQfactor of a resonator.We revealed that the presence of holes lead to a coupling competition dissipation mechanism that responsible for the abnormal enhancement in theQfactors of defected CNTs.Our findings may open new avenues for designing high performance nanoresonators based on imperfect CNTs grown by CVD.

2.Methods

The dissipation characteristic of both perfect and defected CNTs were investigated by carrying out a series of ring-down simulations as illustrated in Fig.1(a) using software package LAMMPS [25].As for the defected CNTs,three kinds of typical defects,including single vacancy(Fig.1(b)),double vacancy(Fig.1(c)),and hole defect(Fig.1(d)),were considered in the present work.The defect concentration is defined as the ratio of removed carbon atoms number to the carbon atoms number of the corresponding perfect CNT.

The interaction between carbon atoms was described with the second generation Brenner potential (REBO-II),as did in our previous research[26].For all performed simulations,the constructed CNT was initially minimized using the conjugate gradient algorithm to eliminate the internal stress arising from model construction stage.Subsequently,the two ends of CNT were fixed,and the CNT was further equilibrated under NVT ensemble [constant number of atoms (N),volume (V),and temperature(T)]using Nose-Hoover thermostat for 500 ps with a timestep 1 fs.Afterwards,the ensemble was switched to a NVE form [constant number of atoms (N),volume (V),and energy (E)],and the CNT was deformed into the first mode shape by applying a sinusoidal displacement profile between the two fixed edges of the CNT,as shown in Fig.1(a).It should be noted that the applied maximum displacement(at the center of CNT) is less then 4% of the CNT length,to make sure that the vibration remains in a linear regime [16,26].Finally,the deformed CNT was allowed to oscillate freely under the energy conserving NVE ensemble,and the trajectories of the center of mass(COM)of CNT were recorded to calculate the resonant frequency(via Fast Fourier Transform(FFT)method) and the corresponding quality(Q)factor.

Fig.1.Schematic description of: (a) perfect carbon nanotube under flexural load,(b) single vacancy defect,(c) double vacancy defect,and (d) hole defect(formed by removing one hexagonal ring).

Similar to our previous works,we estimate theQfactors of CNTs on the basis of root-mean-square (RMS) displacement of the COM,since calculating error induced by thermal motion has already averaged out without further post-processing [16,26].The RMS displacement of CNT takes the expression:

wherexcom,ycom,andzcomare the displacement of COM of CNT in thex,y,andzdirection,respectively.Assuming that the vibration is a single dominant mode,then the decay of RMS displacement of COM of CNT follows an exponential pattern,namelyRMS∝e-ζωt,where ζ is the damping ratio and ω represents the angular frequency of the CNT vibration.As a result,theQfactor can be ultimately determined viaQ＝1/2ζ.

3.Results and discussion

3.1.Pristine carbon nanotubes

Before investigating the effect of defects on the dissipation of CNTs,we initially analyzed the intrinsic dissipation of pristine CNTs in order to not only validate our simulation approach but also provide insights into the origins of energy dissipation for CNT resonators.Two 15 nm long single layer CNTs,i.e.,(12,12) and (20,0) CNT,were considered to achieve the above mentioned purpose.

The typical RMS decaying profile of CNT operated at low temperature(10 K)and room temperature(300 K)is shown in Fig.2(a)and Fig.2(b),respectively.It is clear that the RMS displacement decays with increasing oscillating cycles (or vibration time),indicating that the external mechanical energy induced by the applied flexural load converted into the internal energy of CNT,resulting in so-called intrinsic energy dissipation.Moreover,the RMS displacement of CNT decays more sharply at room temperature than that at low temperature 10 K.As can be seen from Fig.2(a)and(b),within 3.0 ns,the CNT RMS displacement decays from 1.25 Å to 1.19 Å at temperature 10 K,whereas decays from 1.25 Å to 0.07 Å at room temperature.Another striking feature is that the RMS displacement decaying trends agree well with exponential pattern,implying that theQfactors determined under the assumption of single dominant mode vibration is reasonable.

Using the FFT algorithm,the resonant frequency of CNTs can be calculated (see Fig.2(c)),and then theQfactors for pristine CNTs at different temperatures can be correspondingly determined,which is presented in Fig.2(d).It can be observed thatQfactors of CNTs decrease significantly with temperature,following a temperature dependenceQ∝T-α,in which the scaling factor α is 1.07 and 0.9 for(12,12)and(20,0)CNT,respectively.The temperature dependence ofQfactors for CNTs obtained in this work is very close to the classicalT-1-dependence,which is in well agreement with those work where errors caused by thermal motion are well eliminated[26–28].

In the real world,the energy losses for a nanoresonator mainly originate from two aspects: the extrinsic dissipation related to environmental conditions and boundary conditions (clamping or support) situations,and the intrinsic energy dissipations which are inherent in any materials.In our simulations,the CNT nanoresonators were operated at vacuum environment such that the extrinsic energy loss caused by environment can be neglected[29].Besides,the clamping dissipation is eliminated because the two fixed edges of the CNT used in our simulations cannot allow for the acoustic energy flow through support ends.Note that although the velocities of these atoms at the two fixed edges are fixed,these atoms can also interact with nearby free atoms via potential.Regarding this fact,the clamped-clamped nanobeams are somewhat different from the macro-scale counterparts.

Fig.2.(a)Decaying of RMS displacement of(12,12)CNT at temperature 10 K,(b)decaying of RMS displacement of(12,12)CNT at temperature 300 K,(c)the nearly temperature-independent resonant frequency of (12,12) and (20,0) CNTs,(d) Q factors as a function of temperatures for CNTs.

Hence,the origin of energy dissipation for CNTs in this work is the intrinsic energy losses.In this regard,the intrinsic energy dissipation is due mainly to the entropy flux due to the heat conduction(thermoelastic damping) for pristine CNTs in the studied temperature range,see the review article[14]and references therein.Namely,these intrinsic energy dissipations are driven by the uneven spatial distribution of temperature.Note that the “driving force” or thermodynamic force in the intrinsic energy dissipation process is thermal gradient,∇T.

The entropy can be defined as

whereTis the absolute temperature,W is the total energy andsis the entropy per unit volume.For a unit volume,the rate of change of the entropy,˙s,can stem from two parts:the entropy flux across the surface of the unit volume and the rate of the entropy generation γ.That is,we obtain

Here the entropy flux,h,can be obtained as

where q is the heat flux,which can be used by,for example,the Fourier(and non-Fourier) heat conduction equation.Recalling the definition of the entropy flux in equation(4)and using the relation:

equation(3)can be rewritten as

In the case of isolated,isothermal,and pristine CNTs,the entropy flux due to the driving force,∇T,will be transformed into the irreversible entropy generation according to the second law of thermodynamics,that is,

Thus,substituting equation(7)back to(6),the rate of change of the entropy shall satisfy

For a period of vibration,the mechanical energy loss due to the irreversible entropy generation inside the whole body of pristine CNTs can be expressed as

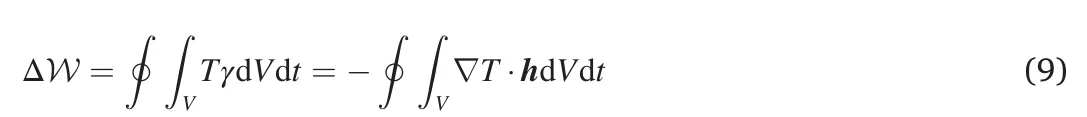
The quality factor of pristine CNTs can then be predicted by

Substituting equation (9) into equation (10),we can obtain the quality factor due to thethermoelastic damping.Note that non-Fourier heat flux is possible to be taken into consideration due to the feature size of CNTs is at nanoscale.

For the flexural vibration,the strain field within a CNT resonator is not uniform and changes along the lateral direction.The non-uniform strain field in CNT leads to a spatial temperature gradient or thermodynamic force (∇T),which in turn results in thermodynamic flux,h.As shown in equation(7),the thermodynamic force and flux can lead to an irreversible entropy generation and therefore reduce the quality factor,as predicted by equation (10).Next,we will show that the thermodynamic force,∇T,may be suppressed by introducing suitable defects in CNTs.

3.2.Defected carbon nanotubes

The CVD synthesis process will inevitably introduce various defects onto the CNTs’surface.In presence of defects,the perfect hexagonal ring structure of CNT around these defects is destroyed.For these carbon atoms at the defect edge or surrounding defects,additional (defectioninduced)strain,e,around defects is generated,even for the case of loadfree defected CNTs.When applying stress fields,the rate of change of the defection-induced strain field per unit volume,˙e,is due to the rate of strain generation around defects:

where E is the rate of strain generation.The strain generation around defects is derived by the corresponding defect-induced stress,σ:

where D is a four-order reaction tensor.Thus,the thermodynamic force in the defected energy dissipation process can be considered as the defection-induced stress field.

In the case of isolated,isothermal,and defected CNTs,the energy flow of both the defect dissipation and the thermoelastic damping (as discussed previously) will be transformed into the irreversible entropy generation,that is,

where the entropy generation in equation(3),γ,have to be composed of two parts: the entropy generation γthdue to the thermoelastic damping and the entropy generation γdefdue to the defect dissipation.Of particular interest is that the effects of the entropy flux h and the rate of production of the defection-induced strain E cannot be simply summarized and have to be taken into account in a coupled way.This is because defects can suppress the heat flux though the big hole due to defects,however,the heat flux will increase the rate of production of defection-induced strain.This study will show that thecoupling effectmay enhance the quality factor of CNT by choosing suitable spatial distribution of defects.

For defected CNTs,the mechanical energy loss inside the whole body for a period of vibration can be obtained as the following form by using equation(13).

With the help of equation (14),the quality factor of defected CNTs can be predicted by definition(10).

To investigate the defect effects on CNT dissipation,here we consider three representative defect types observed in CVD synthesized CNTs,namely the single vacancy,double vacancy,and hole defect.The source tube is a 15 nm long (20,0) CNT and the defect concentration for these three defect types was kept the same as 1%.For every defect type studied here,theQfactor of defected CNT is the averages over at least five replicas.It should be noted that the defected CNT model was constructed by randomly generating a few specific defects onto the CNT surface.The number of deleted carbon atomnto form the hole defect is used to characterize the hole defects studied in our simulations.To reduce computational resources needed,the simulation temperature for all the following simulations is 300 K unless otherwise stated.

TheQfactors for perfect and defected(20,0)CNTs at 300 K are shown in Fig.3.It can be observed that defects have significant effects on theQfactors of CNTs.The defected CNTs with SV,DV or hole defects have a lowerQfactor(average value)than that of perfect CNT,implying that the presence of randomly distributed defects generally enhanced the energy dissipation of CNT.The decreasing trend ofQfactors of CNTs due to the presence of defects has also been demonstrated by experiments carried out by Zhang et al.in which CNTs of higher defects density(controlled by electron irradiation time) possess lowerQfactors [22].The deleterious effect of defects onQfactor of CNTs mainly originates from the vibrational mismatch between edge atoms in the defects zone and other atoms in the interior of CNT.As suggested by Kim and Park,the vibration state of those free edge carbon atoms greatly differ from the interior atoms due to the lack of bonding neighbors,leading to spurious edge modes that can significantly enhance the intrinsic dissipation rate of low-dimensional carbon nanomaterials including graphenes and CNTs [30].

Overall,CNTs show lowerQfactors due to the presence of randomly distributed defects.However,we find an interesting phenomenon from Fig.3 that CNTs with hole defect possessQfactors higher than that of CNTs with SV and DV.Particularly,in some cases,the CNTs with hole defects can yieldQfactors comparable to or even higher than that of perfect CNT.This observation somewhat contradicts to the common notion that internal defects usually reduce theQfactors of a material because the additional defect dissipation is introduced.

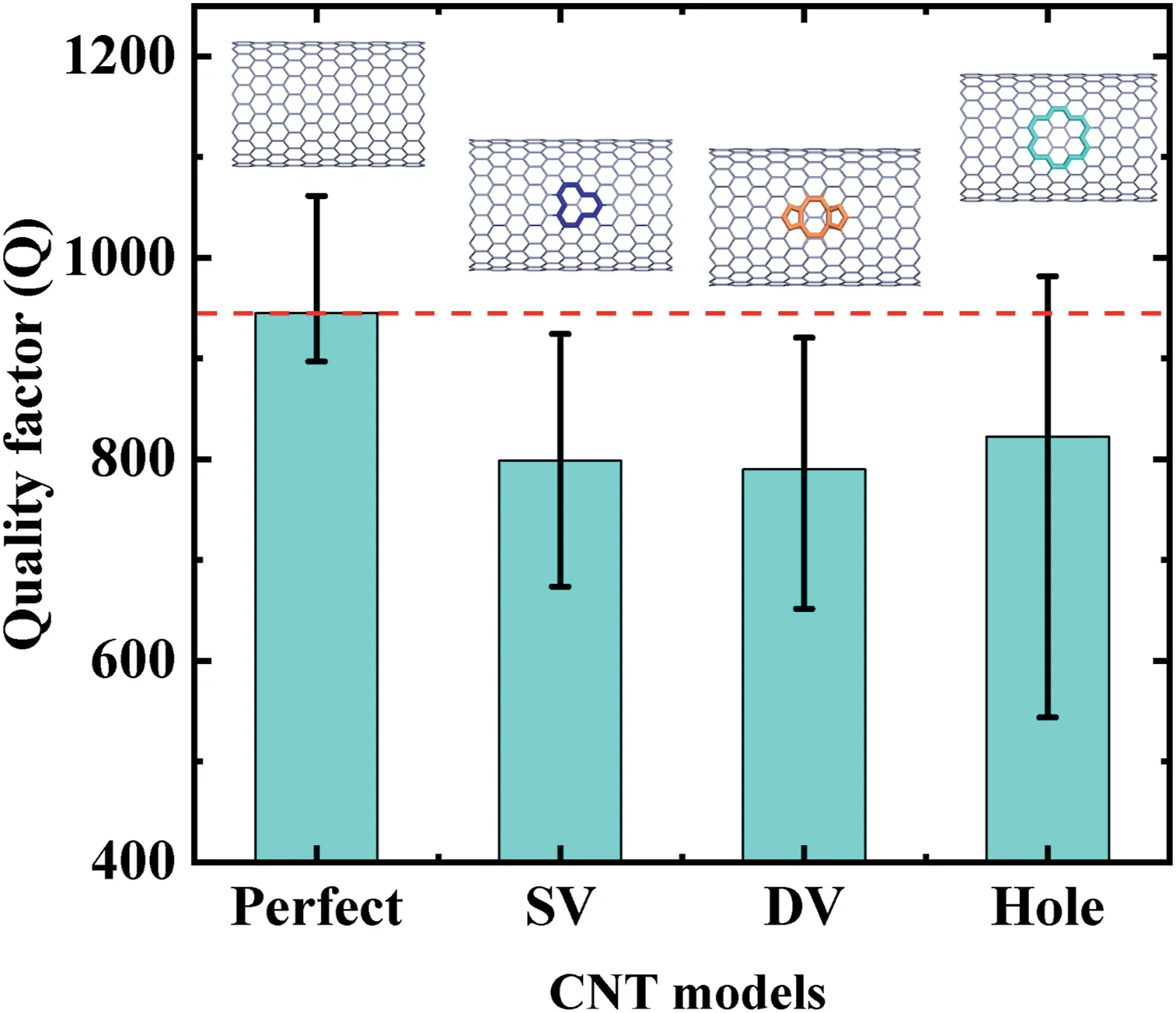
Fig.3.Comparison of Q factors between pristine (20,0) CNT and defected(20,0) CNTs having different type of randomly distributed defects.

Fig.4.Schematical illustration of the coupling competition mechanism between the defected atomic mismatch and the thermoelastic dissipation.

Due to the simple fact that the quality factor due to the defect mechanism is always positive,the only possible explanation for the abnormalQfactor of CNTs with hole defects is that there exhibits acoupling competition mechanismbetween the defect dissipation and the thermoelastic damping,as schematically illustrated in Fig.4.On one hand,the different vibrational frequencies of free edge atoms in the defects introduced an additional energy dissipation source due to the atom mismatch between the nearby and away defect domains,which can reduce theQfactor of CNT.On the other hand,the presence of hole defects may influence the dissipation rate arisen from the thermoelastic dissipation.It is well known that internal defects can play a crucial role in affecting the strain state of nanomaterials of nanostructures,especially for the single-layer CNT or graphene.According to the thermoelastic dissipation discussed in subsection 3.1,the spatial strain field within a nanoresonator is critical in determining the rate of converting mechanical vibration energy to heat.In particular,for the thermoelastic dissipation,the spatial temperature gradient or the entropy flux is highly related to the non-uniform strain field in the case of flexural vibration.Thus,if the strain gradient within CNT and correspondingly temperature gradient(thermodynamic force)are greatly reduced due to the presence of hole defects,the thermoelastic dissipation can be significantly suppressed.

3.3.Defects engineering for CNT damping design

If the proposed coupling competition mechanism induced by CNT hole defects holds true,we can infer that the damping characteristic of CNT can be tuned via defect engineering.To verify the proposed coupling competition mechanism,we further investigated the effects of hole defects on the intrinsic dissipation of CNT through changing the size and position of holes.As shown in Fig.5(a),four holes of the same size were distributed in a symmetric and horizontal (hole center) manner.Two parameters were used to characterize the introduced hole defects,namely the hole size parameternand hole position parameter α,in whichnrepresents the number of deleted carbon atoms to form the hole and α is the ratio of the distance between hole center and the fixed edge to the half of CNT length,as illustrated in Fig.5(a).

We firstly varied the hole sizenfrom 2 to 65 with a constant hole position parameter α of 0.22 (the holes are near the boundaries) to investigate the hole size effects on CNT dissipation.TheQfactor and resonant frequency of CNTs as a function of hole sizenis shown in Fig.5(b).It is seen that the resonant frequency of CNTs decreases almost linearly with increasing hole size,which is mainly attributed to the deterioration effects of hole defect on the elastic modulus of CNT[22].As hole sizenincreases,the number of carbon atoms at the free edges of the holes increases gradually,indicating a higher defects dissipation.However,we observe surprisingly from Fig.5(b) that theQfactor of CNT shows an abnormal increase as hole size increases when the hole sizenis less than 42.When the hole sizenis greater than 42,theQfactor of CNT decreases asnfurther increases.More importantly,these CNTs which contain holes with hole sizenexceeds 16 possessQfactors higher than that of perfect CNT.For instance,the CNT of hole sizen＝42 has an averageQfactor of 2009,which is 113%greater than theQfactor(945)exhibited by perfect CNT.This phenomenon strongly demonstrated the existence of the proposed coupling competition mechanism that,although an additional defect dissipation source is introduced due to the presence of hole defects,these thole defects with proper size and position are,however,able to reduce the thermoelastic dissipation and ultimately leads to an overall higherQfactor of defected CNTs.

In the case of flexural vibration,the non-uniform strain field is critical in determining the thermoelastic dissipation.Therefore,we plot the stress distribution(the atomic stress arisen from thermal fluctuation was excluded)in a perfect CNT and defected CNTs with 4 holes to explore the underlying mechanism responsible for the coupling competition mechanism.As is shown in Fig.6(a),the stress varies linearly along the lateral direction and maximum stress gradient (and thus strain gradient)occurred at the middle and two ends of CNT.Therefore,the flow of energy at the boundaries and middle of CNT becomes more apparent,which contributes to most of the dissipated energy due to the thermoelastic.In the presence of 4 holes (n＝42) near the boundaries,as can be seen in Fig.6(b),the strain gradient corresponding to the stress contour within the defected CNT is significantly reduced especially at the middle and boundaries,implying that the dissipation due to the thermoelastic damping can be greatly suppressed.

The variation of resonant frequencies andQfactors of CNTs with the hole position parameter α are shown in Fig.5(c).The hole size was kept the same asn＝42.As the holes move toward the middle of CNT,the resonant frequency increases continuously whereasQfactors attain its maximum value at a proper position(α ＝0.22 for the studied cases).The effect of hole position on theQfactor of CNT can be understood in terms of the proposed coupling competition mechanism.Since the physical origin of the defect dissipation is the vibrational mismatch between the free edge atoms and interior atoms,it is reasonable to assume that the hole position has negligible effect on the defect dissipation due to the identical hole size.As for the thermoelastic dissipation,one can observe from the comparison of Fig.6(b)and(c)that when holes are close to the CNT middle,the strain gradient becomes more apparent within the CNT,particularly at the boundaries and middle of CNT.This phenomenon indicates that holes with proper positions (near but not too close to the boundaries) are preferred to attain lower energy dissipation stemming from the thermoelastic damping,which can ultimately achieve higherQfactor of defected CNTs.

4.Conclusions

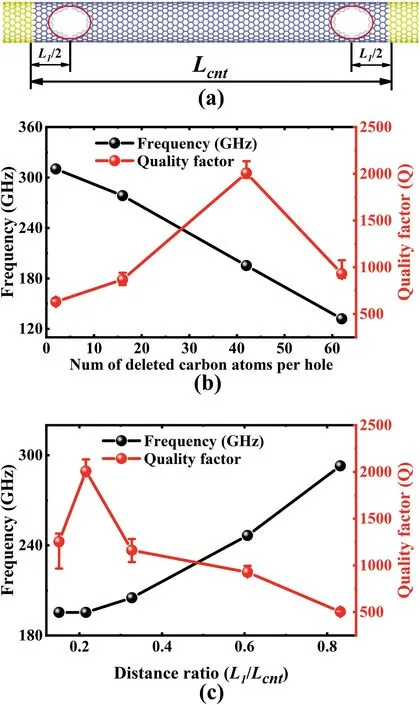
Fig.5.The effects of defect engineering on CNT dissipation characteristic,(a)schematic view of CNT containing four symmetric distributed holes,(b) the resonant frequency and Q factor of CNTs as a function of hole size n(the position parameter α is 0.22),(c) the resonant frequency and Q factor of CNTs as a function of hole position parameter α (the hole size n ＝42).

Fig.6.The contour of stress distribution for (a) perfect CNT,(b) CNT with 4 holes of hole size n ＝42 and hole position parameter α ＝0.2,(c) CNT with 4 holes of hole size n ＝42 and hole position parameter α ＝0.83.

In summary,we have investigated the effects of various defect types on the dissipation characteristic of CNTs and demonstrated for the first time that the quality factors (Qfactors) can be tailored via defect engineering.Despite randomly distributed defects will decrease theQfactor of CNTs,we found surprisingly that theQfactors of these defected CNTs can be enhanced by more than 113%in the presence of hole defects with suitable size and position.This abnormal enhancement observed in theQfactor of defected CNTs is in strongly contradiction to the commonly held notion that defects will introduce an additional defect dissipation sources and thus reduce theQfactors of resonators.

By analyzing the strain distribution of CNTs,we find that hole defects exhibit a coupling competition mechanism on theQfactors of defected CNTs,which is responsible for the abnormal enhancement inQfactors.In the presence of hole defects,especially at the boundaries,the strain gradient within CNT and correspondingly temperature gradient (thermodynamic force)is greatly reduced,leading to lower dissipation arisen from the heat conduction,and thus compensating the detrimental effect of the defect dissipation on the overallQfactor of CNT.Since high precision defect handling techniques become possible,we believe that our findings provide a new route for the design of property-tunable CNTbased nanoresonators with high performance.

Declaration of competing interest

The authors declare that they have no conflict of interest.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (Grant Nos.51605172 and 51775201),the Natural Science Foundation of Hubei Province (Grant No.2016CFB191),the Fundamental Research Funds for the Central Universities (Grant No.2015MS014),and the Hong Kong Scholars Program (No.XJ2020043).Computational resources from the National Supercomputer Center in Lvliang and Guangzhou of China are also gratefully acknowledged.