Atomic insights into synergistic effect of pillared graphene by carbon nanotube on the mechanical properties of polymer nanocomposites

Zhipng Zhou ,Hng Zhng ,Jili Qiu ,Pngwn Chn ,Wifu Sun,*

a State Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology,Beijing,100081,China

b Beijing Institute of Technology Chongqing Innovation Center,Chongqing,401120,China

c School of Mechatronic Engineering,Beijing Institute of Technology,Beijing,100081,China

d Explosion Protection and Emergency Disposal Technology Engineering Research Center of the Ministry of Education,China

e Tongda College of Nanjing University of Posts & Telecommunications,Yangzhou,225127,China

Keywords:Molecular dynamics Carbon nanotube Pillared graphene Synergistic effect Polymer nanocomposite

ABSTRACT Molecular dynamics simulations have been performed to explore the underlying synergistic mechanism of pillared graphene or non-covalent connected graphene and carbon nanotubes (CNTs) on the mechanical properties of polyethylene (PE) nanocomposites.By constructing the pillared graphene model and CNTs/graphene model,the effect of the structure,arrangement and dispersion of hybrid fillers on the tensile mechanical properties of PE nanocomposites was studied.The results show that the pillared graphene/PE nanocomposites exhibit higher Young’s modulus,tensile strength and elongation at break than non-covalent connected CNTs/graphene/PE nanocomposites.The pull-out simulations show that pillared graphene by CNTs has both large interfacial load and long displacement due to the mixed modes of shear separation and normal separation.Additionally,pillared graphene can not only inhibit agglomeration but also form a compact effective thickness (stiff layer),consistent with the adsorption behavior and improved interfacial energy between pillared graphene and PE matrix.

1.Introduction

As an important member of the family of carbon nanomaterials with hexagonal aromatic structures,either one-dimensional carbon nanotubes(CNTs) or two-dimensional graphene has demonstrated a number of intriguing properties for a wide range of applications,including hydrogen storage,gas sensors,nanoelectro-mechanical systems(NEMS),energy storage and high performance nanocomposites[1–6].Numerous experimental studies on the mechanical properties of polymer composites reinforced by graphene or CNTs have been reported [7–10].Although remarkable progress has been made in the CNTs or graphene reinforced polymer nanocomposites,the potential applications of CNTs and graphene in polymer nanocomposites are hindered because of entanglement of CNTs or agglomeration/restacking of graphene[11–13].The hybrid fillers composed of CNTs and graphene is one of the most attractive ways to address these obstacles from a structural point of view.As most recently reported[14,15],hybrids composed of CNTs and graphene have demonstrated significant synergistic effects in thermal transport properties,electrochemical activity and mechanical properties.The unique three-dimensional (3-D) hybrid structures of hybrid fillers(CNTs and graphene) can improve dispersion [16,17] and enhance interfacial properties[17,18]to achieve excellent reinforced composites.In particular,hybrid fillers with covalent structure (pillared graphene)[19] have shown better properties than noncovalent structure(CNTs/graphene) [20].Although more and more experimental studies have reported on pillared graphene reinforced polymer nanocomposites,nonetheless most of the reported studies have focused on low weight fraction of CNTs and graphene.Meanwhile,it is difficult to accurately control the dispersion at high weight fraction of fillers,and quantitatively measure the interfacial properties between carbon nanofillers and molecular chains by experiment.This leads to widely scattered and discrete experimental results and limits the understanding of reinforcing mechanisms.As a result,exploring the influence of dispersion of pillared graphene at high weight fraction and interfacial behavior between pillared graphene and matrix is of great value for the production and application of high performance nanocomposites.

Fig.1.Variable setting and initial spatial distribution for two types of PG/PE models.(a) Morphology and arrangement model of filler (28 wt%): the length of CNT (L),the number (N) and the distance (d) of PG layers are set as variables.L1-N1-d1-PG/PE,L2-N1-d1-PG/PE and L3-N1-d1-PG/PE model with short,medium and long CNT,respectively;L1-N2-d2-PG/PE model with small distance and two layers of PG;L1-N2-d3-PG/PE models with large distance and two layers of PG;L1-N3-d3-PG/PE model with large distance and three layers of PG.(b) Random dispersion model of filler: the weight fraction and the degree of dispersion of PGs are set as variables.C–I,C-II and CIII contain 3,5 and 7 basic units of PG respectively(uniform dispersion);C-IV contains 5 basic units of PG(agglomeration) for comparison.

Molecular dynamics(MD)simulations,as an alternative approach to experiments,have been considered as a powerful and reliable method to investigate material properties and further explain the underlying mechanism from atomic/molecular scale.A number of studies have been reported on the mechanical properties of carbon nanofiller-based polymer nanocomposites by MD simulation [21–23].Due to the high computational cost,most of the works focused on the interfacial properties by modelling the small-sized models,and only a small amount of work was to explore the influence of filler dispersion on the mechanical properties of nanocomposites [24–26].So far seldom efforts have been made to unravel the underlying mechanism governing the mechanical property enhancement intrigued by the unique 3D structure and better dispersion of pillared graphene.What’s more,only a few studies reported on pillared graphene/polymer composites interfacial properties[23,27].Meanwhile,although the synergistic effect of hybrids composed of CNTs and graphene has been widely recognized,nonetheless the intrinsic mechanism of the synergistic effect from the atomic scale remains largely unknown.Hence,it is of great significance to systematically study the influences of pillared graphene dispersion and interface properties on the mechanical properties of polymer nanocomposites and to reveal the intrinsic mechanism of synergistic effect.

In this work,pillared graphene/PE model and dispersed CNTs/graphene/PE model are constructed based on the MD method.The effect of morphology,arrangement,weigh fraction and dispersion of hybrids on the Young’s modulus,tensile strength and elongation at break of PE nanocomposites will be firstly studied by tensile tests.Then,the interfacial properties between hybrid filler and PE matrix were studied through adsorption behavior,pull-out force and interfacial energy,and the synergistic enhancement mechanism of pillared graphene is explained.Finally,the effective thickness is confirmed by calculating atomic number density and radial distribution function (RDF) and the synergistic mechanism of pillared graphene is further clarified from the effective thickness theory.

2.Simulation method and conditions

2.1.Morphology and arrangement model of filler

Fig.2.Stress-strain curves for multiple models.(a) pure PE,PG/PE model and dispersed CNTs/graphene/PE model;(b) the models with different length of CNTs,different number of PG layers and different distances between the PG layers.

The molecular model was constructed using the Amorphous Cell Package in Materials Studio 7.0.All MD simulations were performed using the large-scale atomic/molecular massively parallel simulator(LAMMPS) [28] code.The PCFF force field was used to describe the interfacial atomistic interactions between polymer and carbon nanofillers.The detailed simulation procedure can be referred to the supplementary information.Fig.S1 shows the hybridization strategy of pillared graphene.In order to reveal the synergistic effect of the morphology and arrangement of pillared graphene in enhancing the mechanical properties of polymer nanocomposites,the pillared graphene/PE (PG/PE)model (Fig.1a) and dispersed CNTs/graphene/PE model (Fig.S2) with the same weight fraction(28 wt%)were engineered.The graphene(44.3× 66.9 Å2),armchair (6,6) single-walled CNTs and pillared graphene(PG) were used as nanofillers.As shown in Fig.1a,a single pillared graphene is composed of a single-layer graphene with an infinite size and six CNTs.The CNTs were covalently connected to both sides of the graphene at equal intervals,and three were grown on each side.For a detailed description of the dispersed CNTs/graphene/PE model,please refer to the supplementary information.

The correlation between the morphology arrangement of pillared graphene and the properties of polymer nanocomposites remains unclear.Therefore,the effect of the length of CNTs (L),the number of PG layers(N)and the distance between the PG layers(d)on the mechanical properties of polymer composites has been explored.The setting of variables in the PG/PE model can refer to Fig.1a.As shown in Fig.1a,PG/PE models with different length of CNTs (L1-N1-d1-PG/PE,L2-N1-d1-PG/PE and L3-N1-d1-PG/PE),different distances between PG layers(L1-N2-d2-PG/PE and L1-N2-d3-PG/PE) and different numbers of PG layers (L1-N1-d1-PG/PE,L1-N2-d3-PG/PE and L1-N3-d3-PG/PE) were engineered separately.

2.2.Random dispersion model of filler

In order to explore the effect of the weight fraction and dispersion of pillared graphene (PG) on the mechanical properties of polymer composites,multiple dispersed pillared graphene/PE(M-PG/PE)models and multiple dispersed CNTs/graphene/PE (M-CNTs/graphene/PE) models have been engineered.In order to save computational time and incorporate as many pillared graphene as possible into a cell,the basic unit of PG was selected as the research object(Fig.1b).As shown in Fig.1b,this PG unit consists of one graphene and one CNT[23].In these models,the graphene(22.1×28.4 Å2),armchair(6,6)single-walled CNT(SWCNT)and pillared graphene contain 266,312 and 594 carbon atoms,respectively.The dispersion systems used in this work has been denoted and their corresponding filler weight fraction are listed in Table S1.We have considered three different weight fractions for each category of dispersion model.Fig.1b and Fig.S3 shows the initial configuration of M-PG/PE model and M-CNT/graphene/PE model (spatial configuration-type group A).The initial configurations of dispersed hybrid filler/PE model (type group B and C) are shown in the Supplementary Fig.S4 and Fig.S5,respectively.According to the fillers type(pillared graphene or CNTs/graphene),the dispersion model was grouped into PG/PE tensile model (Fig.1d) and CNTs/graphene/PE tensile model(Fig.S3).And according to the dispersion degree of fillers,the dispersion model was divided into uniform dispersion model (C–I,C-II,C-III in Fig.1b and N–I,N-II,N-III in Fig.S3) and agglomeration model(C-IV in Fig.1b and N-IV in Fig.S3).A set of spatial distributions of either M-PG/PE or M-CNTs/graphene/PE tensile model at different weight fractions are shown in Fig.1b(C–I,C-II and C-III)and Fig.S3(N–I,N-II and N-III),respectively.

Fig.3.Stress-strain curves for dispersion model of filler:(a)multiple dispersed pillared graphene/PE models and(b)multiple dispersed CNTs/graphene/PE models.

Table 1 Mechanical properties of different models with or without fillers.

3.Results and discussion

3.1.Mechanical properties

The stress-strain curve(Fig.2 and Fig.3)can be obtained by the virial expression.Fig.2 shown the stress-strain curves for pure PE,CNTs/graphene/PE model and multiple models with different length of CNTs,different number of PG layers and different distances between the PG layers.Fig.3 shown the typical stress-strain curves of dispersion model of filler (multiple dispersed PG/PE models and multiple dispersed CNTs/graphene/PE models).Based on the ASTM E111 standard [29],the Young’s modulus is estimated from the slope of the initial linear part of the stress-stain curves within a strain of 0.5%and the peak value of stress is defined as the tensile strength.The detailed description of the virial expression and stress-strain response are put in the supplementary information.

3.1.1.Effect of morphology and arrangement

Generally,the different morphology and arrangement of reinforcement may lead to a vital impact on the mechanical behavior of polymer nanocomposites.In this work,the pure PE,PG/PE and CNTs/graphene/PE model were subjected to an uniaxial deformation in thezdirection.Based on the stress-strain response,the Young's modulus,tensile strength and elongation at break of above three types of models can be obtained and listed in Table 1.As shown in Table 1,the Young’s modulus,tensile strength and elongation at break for the pure PE were 1.26 GPa,26.7 MPa and 3.54%,respectively,and these are close to the theoretical and experimental results [25,30,31].Besides,it can be observed that the incorporation of pillared graphene results in the improved Young’s modulus and tensile strength of PE nanocomposites.This is mainly attributed to the interlock effect[32]formed between the PE chain and the aligned CNT of pillared graphene.Fig.S6 and Fig.S7 demonstrates the adsorption process of the pillared graphene to the PE chain and the interlock structure,respectively.This interlock effect can transfer the loading of matrix to the graphene through the covalently connected CNTs and provide an additional enhancement mechanism apart from the van der Waals(vdW)interface load transfer between the fillers and polymer matrix [32,33].Furthermore,the interlock effect significantly weakens the mobility of the PE chain [34,35] (Fig.S6 and Fig.S8) and this improves the Yong’s modulus of the PE nanocomposite to certain degree[36,37].The rigid nanofillers tend to reduce the ductility of composites[17].Moreover,the adsorption of CNT on the surface of graphene results in a lower the elongation at break of CNTs/graphene/PE model(1.92%)than that of L3-N1-d1-PG/PE model(2.23%)(Fig.S2b).It is worth noting that pillared graphene also has a significant effect on improving the thermal conductivity of polymer nanocomposites.The thermal conductivity of PG/PE model is always greater than that of CNTs/graphene/PE model at different temperatures(Figs.S9–S10).

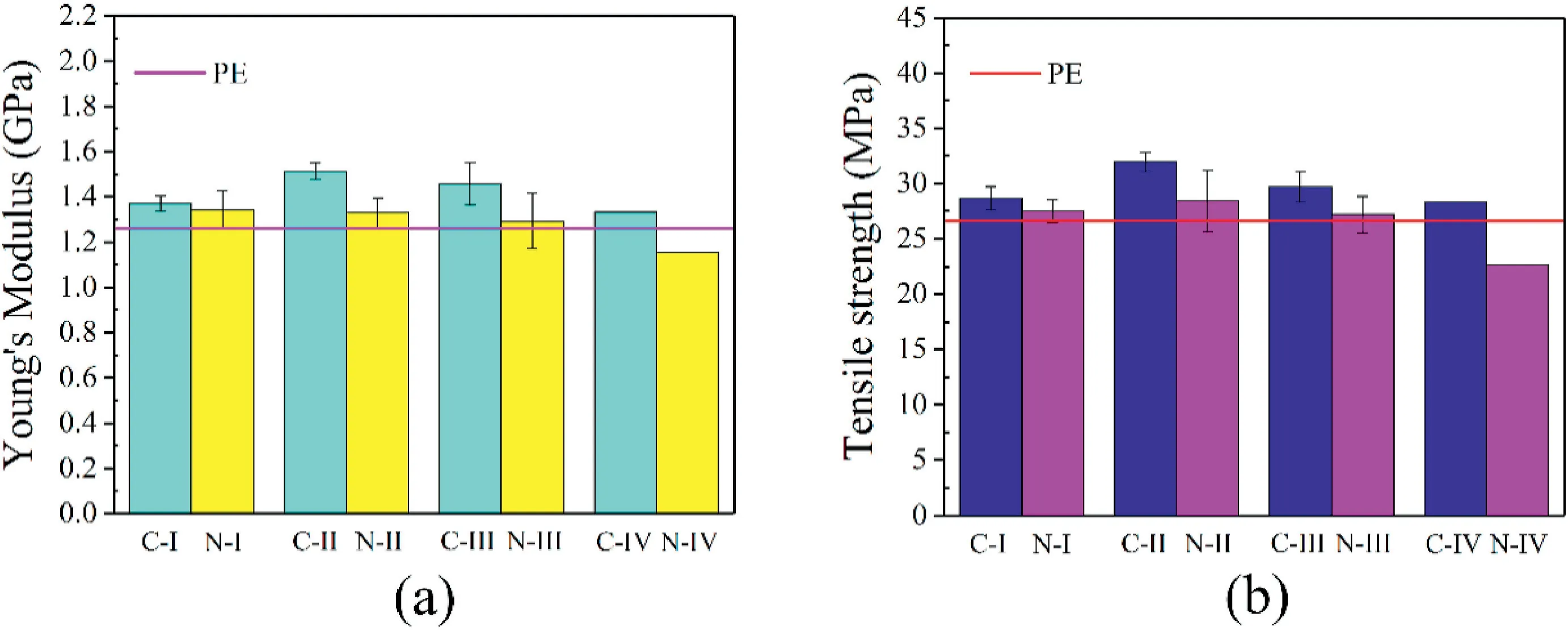
Fig.4.(a) Young’s modulus and (b) tensile strength of pure PE,pillared graphene/PE and CNTs/graphene/PE models.

Fig.5.Spatial distribution for (a) pillared graphene/PE and (c) CNTs/graphene/PE models at 7.07 wt% after full relaxation.The black circle marks the mutually adsorbed fillers;(b) and (d) are the magnified configuration diagrams of the mutually adsorbed pillared graphene and CNTs/graphene,respectively.

As shown in Table 1,the tensile strength,Young's modulus and elongation at break of the PG/PE model all increase first and then decrease as the length of the CNTs increases.L2-N1-d1-PG/PE model delivers the best mechanical properties.In the L1-N1-d1-PG/PE model,the short CNTs cannot effectively limit the mobility of long PE chains.This results in a lower Young's modulus and tensile strength of L1-N1-d1-PG/PE model as compared to L2-N1-d1-PG/PE and L3-N1-d1-PG/PE models.The high mobility of the PE chain results in a higher elongation at break of L1-N1-d1-PG/PE model as compared to L3-N1-d1-PG/PE model.In the L3-N1-d1-PG/PE model,although the long CNT can effectively restrict the movement of the PE chain,the graphene layer is difficult to impose constraints on the distant PE chain.This leads to the lower mechanical properties of L3-N1-d1-PG/PE model compared to L2-N1-d1-PG/PE model.Both CNTs with appropriate length and graphene layer in the L2-N1-d1-PG/PE model can form a better constraint on the PE chains.As shown in Table 1,the multi-layer pillared graphene/PE(L1-N2-d3-PG/PE and L1-N3-d3-PG/PE)model has a higher Young's modulus than the single-layer pillared graphene/PE (L1-N1-d1-PG/PE) model.This indicates that the multi-layer pillared graphene can form a synergistic effect to jointly limit the mobility of the PE chains.The unique 3D structure of pillared graphene is believed to be the origin of the underlying synergistic mechanism [38].An ordered intercalated morphology of CNTs can reduced considerably self-aggregation of graphene [33].However,the distribution of nanofillers plays an important role in the system [21].During the relaxation process,the spatial distribution of the pillared graphene will inevitably change.This uncontrollable spatial distribution plays a key role in the mechanical properties of nanocomposites.This can explain why the tensile strength and elongation at break of the model in the PG/PE system with different number of PG layers have no regular trend.Moreover,we explored the effect of the distance between pillared graphene on the mechanical properties of PE composites.As shown in Table 1,the mechanical properties of L1-N2-d2-PG/PE model are significantly lower than that of L1-N2-d3-PG/PE model.This indicates that stacked pillared graphene can cause a decrease in the enhancement effect for nanocomposites.However,the Young's modulus and tensile strength of the stacked pillared graphene/PE are still greater than that of pure PE.This is mainly because the aligned CNTs grown on the surface of pillared graphene can increase the spacing and weaken the π-π interactions between pillared graphene compared to the extremely small spacing of the stacked graphene(0.334 nm)[39].The aligned CNTs in the pillared graphene makes the stress distribution in PG/PE model more uniform.The uniformly distributed stress state avoids the rapid instability and destruction of nanocomposites.

3.1.2.Effect of weigh fraction and hybrid type

In this work,the effect of hybrid type and dispersion degree of nanofiller on the mechanical properties of M-PG/PE or M-CNTs/graphene/PE polymer nanocomposites were investigated.Fig.4 shows the Young’s modulus (Fig.4a) and tensile strength (Fig.4b) of M-PG/PE models and M-CNTs/graphene/PE models.For the case of pillared graphene reinforced polymer nanocomposites,with the increase of the weight fraction,the Young’s modulus and tensile strength have gradually increased from 1.37 GPa to 28.68 MPa at 3.16 wt% to the optimized value of 1.51 GPa and 31.96 MPa at 5.15 wt%,respectively,followed by decreasing to 1.45 GPa and 29.73 MPa at 7.07 wt%,respectively.For given the similar weight fraction of nanofillers,as compared with the non-covalently connected CNTs/graphene/PE nanocomposites,the Young’s modulus and tensile strength of covalently connected PG/PE polymer nanocomposites are higher than those of the non-covalently connected ones.This result is consistent with the reported experimental results [17] and obvious synergistic effect of 3D graphene and CNTs has been demonstrated for polymer nanocomposite.This mainly because unique 3D structure of pillared graphene facilitates the dispersion and enhances interfacial properties between fillers and matrix.Although pillared graphene can significantly improve the dispersion,it is inevitable to avoid mutual adsorption between the pillared graphene at high weight fraction of 7.07 wt%(Fig.5a).This leads to a decrease in the Young's modulus and tensile strength of the pillared graphene/PE nanocomposites.

The improved dispersion of pillared graphene can be supported by comparing the Fig.5a and c.From Fig.5a,it can be observed that only one group of fillers are adsorbed in the PG/PE model.But from Fig.5c,it can be observed that three groups of fillers are adsorbed in the CNTs/graphene/PE model.This indicates that the probability of adsorption between pillared graphene is lower than that between graphene and CNTs under the same weight fraction.After adsorption occurs,graphene is fully in contact with CNTs in the CNTs/graphene/PE system(Fig.5d),while pillared graphene has only a small area overlap due to its unique three-dimensional structure and self-supporting effect [16] (Fig.5b).This is one of the important reasons why PG/PE composites have higher Young’s modulus and tensile strength than CNTs/graphene/PE nanocomposites.In the agglomeration model,the agglomerated CNTs/graphene exhibits an adverse effect on the Young’s modulus and tensile strength of nanocomposites at 5.03 wt%,which become lower than those of pure PE.Amazingly,for the case of 5.15 wt%,the Young’s modulus and tensile strength of PG/PE nanocomposites attain 1.33 GPa and 28.30 MPa,respectively (Fig.4a–b).The agglomerated pillared graphene still demonstrates a moderate enhancement effect on the Young’s modulus and tensile strength of nanocomposites.This indicates that even in the agglomeration model,the self-supporting effect of pillared graphene can still effectively inhibit the decrease of contact area between filler and matrix caused by adsorption.

Fig.6.Elongation at break of pure PE,pillared graphene/PE and CNTs/graphene/PE models.

For most materials,there is an intrinsic trade-off between strength and toughness.Although carbon nanofillers can improve the strength of polymer composites,it is often at the expense of material extensibility[16,40].As shown in Fig.6,except that the elongation at break of the C-II model is basically equal to that of pure PE,the elongation at break of all the other systems is lower than that of pure PE.As we all know,the large deformation can dissipate more fracture energy.The decrease of elongation at break may result in the loss of material toughness.However,it can be observed that the elongation at break of C–I,C-II and C-IV models are greater than those of N–I,N-II and N-IV models,respectively,and only the elongation at break of C-III model is basically equal to N-III model.These indicate that pillared graphene can slow down or even completely compensate the loss of extensibility while improving strength of PE nanocomposite.This reconciles the two contradictory attributes of strength and toughness to a certain extent.The pillared graphene exhibits excellent elasticity with large compressive/tensile elastic strain limit.The deformation of graphene is dominated by the bending.Due to the covalent connection,when the CNTs are fixed by the matrix,graphene can shrink in the out-plane direction and dissipate part of the energy,thereby partly compensating for the loss of extensibility [41].

3.2.Interfacial properties

In this work,the pull-out force and interaction energy were used to evaluate the interface properties between filler and PE matrix.As shown in Fig.7a–c,there are three modes of separation of the filler from the matrix in this work:normal separation(mode I),shear separation(mode II)and mixed separation(mode I/II).The mode I/II is composed of mode I and mode II.In order to evaluate the difference between three separation modes,the pull-out forces of graphene/PE pull-out model (Fgra-phene) under mode I,CNT/PE pull-out model (FCNT) under mode II and pillared graphene/PE pull-out model (Fp-graphene) under mode I/II were separately calculated.Normal displacement offers insights into understanding cohesive traction-separation mechanism between filler and polymer matrix whereas shear displacement provides information about the pullout mechanism [21].Fig.7d–f demonstrates the variation of pull-out forces of the graphene/PE,CNT/PE and pillared graphene/PE pull-out model as a function of displacement.As shown in Fig.7d,Fgra-phenefirst increase dramatically with an almost linear trend and then decrease quickly to zero.The maximum pull-out force reaches 3657 pN,but displacement is only 10 Å.The normal separation mode gives a large pull-out force but short displacement.In contrast,FCNTfirst shows a trend of nonlinear growth with a small peak value and then drops to zero after an oscillating downward phase (Fig.7e).The maximum pull-out force and displacement are 586 pN and 41 Å,respectively.The shear separation mode gives a small pull-out force but long displacement.However,pillared graphene delivers a peak pull-out forceFp-grapheneof 4093 pN and a displacement of 40 Å and this indicates that it has combined the advantageous properties of both graphene and CNTs with a both large peak value(＞FCNTandFgraphene)and long displacement (Fig.7f).This can be ascribed to the fact that the unique 3D structure enables pillared graphene/PE pull-out model to experience the other two separation modes(Mode I and Mode II)at the same time.This may provide atomic insights into synergistic effect of pillared graphene in reinforcing polymer nanocomposites.

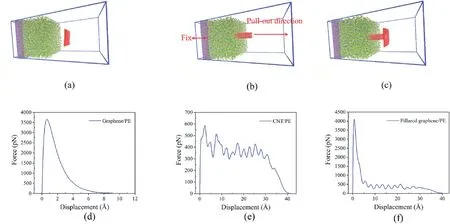
Fig.7.The pull-out models of fillers from PE matrix under(a)mode-I,(b)mode-II and(c)mode I/II,respectively;the force vs displacement curves for(d)graphene/PE,(e) CNTs/PE and (f) pillared graphene/PE models.

Fig.8.The trend diagram of the interface energy between fillers and matrix of pillared graphene/PE and CNTs/graphene/PE models with strain during the tensile process.

The schematic diagram and interaction potential energy calculation are shown in the Fig.8.Throughout the tensile process,the absolute value of interaction potential energy of pillared graphene/PE nanocomposite is always greater than that of CNTs/graphene/PE nanocomposite.The average value of the interaction potential energy of pillared graphene/PE nanocomposite is about 7% greater than that of CNTs/graphene/PE nanocomposite.The negative interaction energy indicates that the PE and the graphene attract each other.This indicates that pillared graphene/PE nanocomposite has stronger interfacial interactions.This is mainly because the self-supporting mechanism of pillared graphene avoids sufficient contact between fillers,thereby inhibiting the reduction in the contact area between the filler and the matrix caused by filler’s adsorption.

3.3.Atomic distribution

In this part of work,the atom number density and radius distribution function (RDF) were analyzed to clarify synergistic mechanisms of pillared graphene.As shown in Fig.9a–b,a fixed-size 3D spaces(black box)was selected to contain CNT parts with the same length in pillared graphene/PE and CNT/PE models,respectively.Subsequently,the C atoms of CNT were defined as central atom and atoms of PE were defined as distribution atom.The atomic number density is defined as the number of atoms within a unit distance(1 Å)along the CNT radial direction(x-axis direction)[42].The atom number density was calculated within selected 3D space,which ensures that the monitoring and statistics of distributed atoms in the two models are within the same size range.The RDF was calculated by using the same method.

As shown in Fig.9c,the distribution of the atom number density around the CNT in the x direction was described.The obvious grooves correspond to the position of CNTs.It can be found that the pillared graphene/PE atom number density model shows a larger atomic number density than the CNT/PE atom number density model.The average atomic number density in pillared graphene/PE model and in the CNT/PE model are obtained to be 96.371 atom/Å and 84.4 atom/Å,respectively.The average atomic density of the pillared graphene/PE model is about 14%higher than that of the CNT/PE model.This is due to fact that atoms of PE are subjected to non-bonding forces from both CNT part and graphene part,resulting in a more compact region.This compact region is called the effective thickness or stiff layer[33,35,37].Meanwhile,due to containing much more atoms,compact effective thickness can also provide larger non-bonding forces acting on the pillared graphene.This may be one of the reasons why pillared graphene/PE nanocomposite has greater interface energy between fillers and PE matrix.This kind of strong interaction provides an insightful avenue to explain synergistic mechanism for improvement of interfacial performance.Generally,the compact effective thickness favors greater Young’s modulus for polymer[32,43,44],which is one of the important reasons for the improvement of Young’s modulus of pillared graphene/PE nanocomposite in tensile simulation.From Fig.S11,it can be observed that more atoms of PE are distributed around the pillared graphene than single CNT.The results of RDF further prove the above conclusion.It is worth noting that the compact effective thickness can also be formed in the CNTs/graphene/PE nanocomposite,but most of the time agglomeration tends to occur when graphene and CNT are very close.This adverse mechanism was inhibited in pillared graphene/PE nanocomposite due to 3D covalent structure and self-supporting effect of pillared graphene.

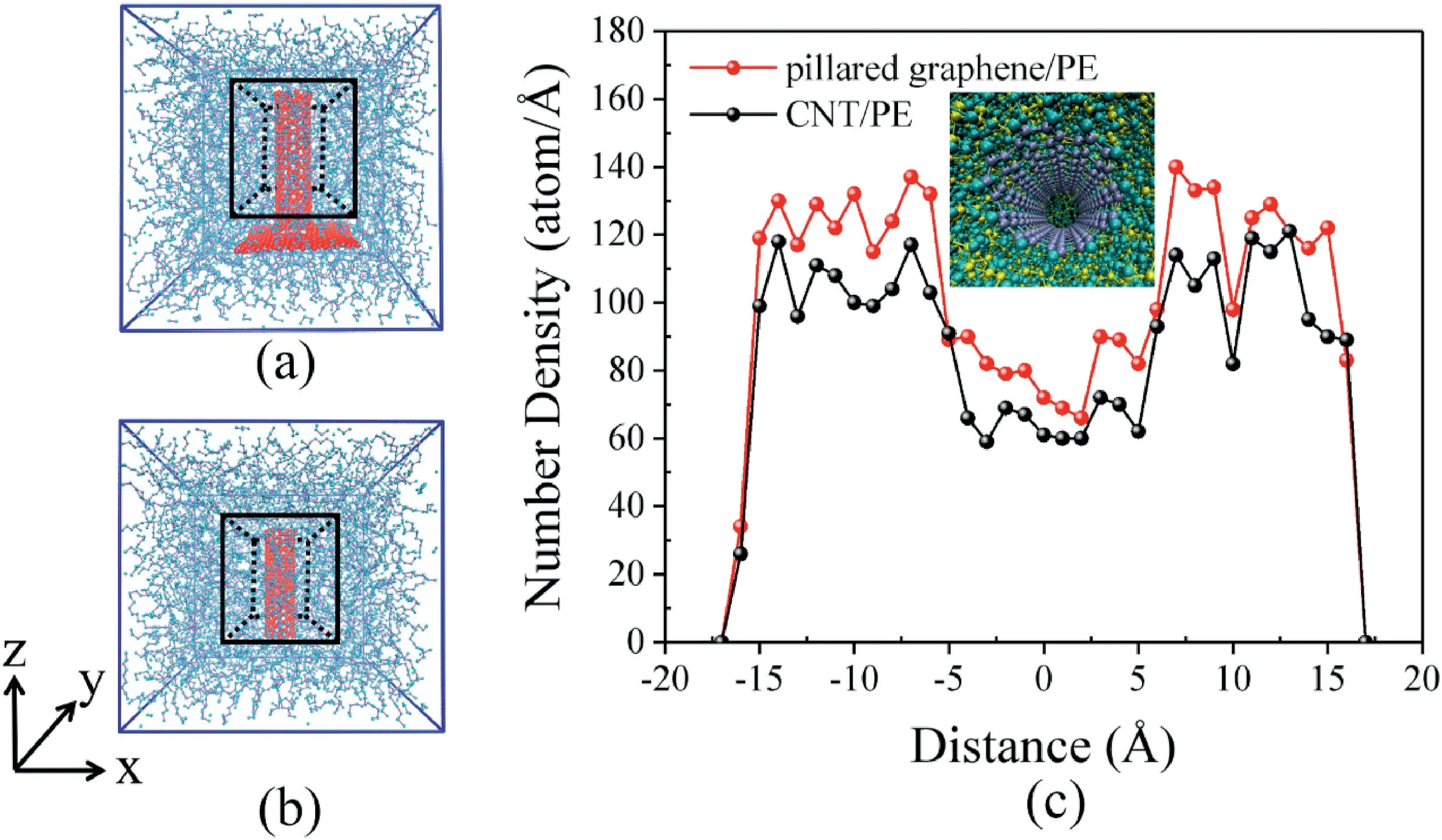
Fig.9.The configuration diagrams of pillared graphene/PE(a)and CNT/PE(b),respectively and the black box is the selected space for calculating the atomic number density around CNT;(c) atomic number density-distance curve for pillared graphene/PE and CNTs/PE models.

4.Conclusion

In this work,MD simulations have been performed to explore the influence of graphene and CNTs hybrid filler in form of different chemical bonding status on mechanical properties of PE of nanocomposites and the underlying synergistic effect of graphene and CNTs have been revealed from atomic level in terms of interfacial properties.Various synergistic mechanisms such as self-supporting,load transfer,mechanical interlocking,mixed separation mode and stiff layer have been proposed and discussed.The simulation results show that the tensile strength,Young's modulus and elongation at break of the pillared graphene/PE composites all increase first and then decrease as the length of the carbon nanotube increases.The multi-layer pillared graphene/PE composites have a higher Young's modulus than the single-layer pillared graphene/PE composites.Compared with CNTs/graphene hybrid,pillared graphene delivers a more significant synergistic effect and this is attributed to the self-supporting mechanism of pillared graphene.In addition,the unique 3D structure of pillared graphene can also form an interlock effect with PE chain and limit the mobility of PE chain.The most significant synergistic enhancement effect on mechanical properties of dispersed pillared graphene/PE nanocomposite has been displayed at 5.15 wt%but is weakened by the agglomeration effect at 7.07 wt%.The pull-out process of pillared graphene from the matrix includes two modes of shear separation and normal separation,which makes pillared graphene have both large interfacial load and long displacement.The existence of compact effective thickness around pillared graphene is confirmed through atomic number density and RDF analysis.The compact effective thickness not only endows the stiffness relative to pure PE,but also confers a strong interface interaction between pillared graphene and matrix.

Declaration of competing interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support from the National Key Research and Development Program of China (grant no.2020YFA0711800),National Natural Science Foundation of China(grant no.11802027,51973033),State Key Laboratory of Explosion Science and Technology (grant no.YPJH20-6,QNKT20-01,JCRC18-01),BITBRFFR Joint Research Program (BITBLR2020018) and Beijing Institute of Technology Research Fund.

Appendix A.Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.nanoms.2021.07.002.