微尺度手性晶格中波传播研究
赵鹏程, 张凯, 傅云婵, 邓子辰
(1.西北工业大学 力学与土木建筑学院,陕西 西安 710072; 2.西北工业大学 复杂系统动力学与控制工业和信息化部重点实验室,陕西 西安 710072)
周期晶格材料具有优异和特殊的力学性能,如超轻、超强、超硬、负刚度、负泊松比或负质量密度等,在航空、航天、机械和土木等工程领域中有广泛的应用[1-3]。周期晶格的力学性能不仅取决于其构成材料,更依赖于精心设计的单胞几何结构,其尺寸范围从纳米级到米级。制造工艺水平的提高进一步推动了微/纳米材料的发展,使其在精密仪器中得到了广泛的应用,如纳米生物传感器、微作动器等先进微/纳工程结构应用[4-5]。研究这些微纳尺度介质的力学行为对于优化设计和提高微尺度构件的力学性能具有重要的意义,如利用微尺度单晶银薄膜提高器件的硬度[6]和微尺度薄镍片提高结构的抗弯强度[7]。同时,利用微尺度周期晶格的动力学特性,尤其是带隙特性,即弹性波被允许或禁止传播的频带,可以实现微/纳尺度机电系统的振动控制及减振隔振。因此,研究微尺度周期晶格的动力学特性具有重要的科学研究价值和广阔的工程应用前景[8]。
大量的研究成果表明,基于宏观理论计算与实验测试得到的微尺度结构的力学特性具有较大差异。并且有相关实验证实,尺寸效应是决定微尺度结构的静态和动态性能的关键因素[9-10]。针对此问题,学术界发展了非局部弹性理论、非局部应变梯度理论和应变梯度理论等来表征微/纳尺度材料的尺寸效应。其中,非局部弹性理论将原子间的长程力概念引入连续介质力学,提出弹性体中一点的应力与弹性体中所有点的应变有关。非局部弹性理论只能表征微尺度构件的刚度软化效应,这与许多实验研究得到的刚度增强效应相互冲突[11-12]。应变梯度理论指出弹性体的应变能是应变及其一、二阶导数的函数,可表征出微尺度构件的刚度增强效应。但该理论中除包含2个经典常数外,还需要确定16个独立的高阶材料常数[13]。结合上述理论,非局部应变梯度理论同时考虑了微尺度弹性体的非梯度非局部弹性应力场和高阶纯应变梯度应力场,描述微尺度构件的力学行为。但该理论需要考虑更为复杂的约束条件[14]。为了减少应变梯度理论中高阶材料常数的数量,学者们通过引入3个材料长度尺度参数,提出了修正的应变梯度理论,以描述微尺度结构的力学特性[10]。然而,这3个材料长度尺度参数难以通过实验测得。更进一步,学术界提出了修正耦合应力理论,通过引入一个尺度参数调节微尺度结构的尺度效应,可有效解决尺寸效应下的欧拉梁、铁木辛柯梁的静态、动态、屈曲和稳定性分析等问题[15-17]。
手性结构是一类广泛存在于自然界中的周期性结构,其优异和特殊的力学性能得到了学术界的高度关注[18-19]。通过对这类周期性结构的设计,可以实现超越柯西弹性理论的自由度,并且在特定频率下实现准静态压扭转换效应[20-21]。此外,还可以通过利用手性结构的压扭耦合特性,实现弹性波的调控[22]。然而,微/纳尺度结构的尺寸效应,对结构波传播特性的影响非常显著,需发展全面、可靠的理论模型用于表征微/纳尺度手性结构的动力学特性和波传播特性。
本文针对具有尺寸效应的微/纳尺度手性周期的波传播特性开展研究。基于修正耦合应力理论,建立微尺度欧拉梁的控制方程,推导考虑尺寸效应的欧拉梁有限单元矩阵,并结合Bloch定理分析微尺度手性晶格的波传播特性。最后,通过与经典理论所得结果比较,研究尺度效应对微尺度手性周期晶格的能带结构、带隙特性和色散面的影响。
1 微尺度手性晶格的动力学模型
1.1 微尺度手性周期晶格几何模型
本文的研究对象为微尺度三、四和六手性周期晶格,其单胞的几何结构如图1所示,将单胞沿着周期性延伸方向(e1和e2方向)进行阵列即可得到无限手性周期晶格。每个单胞的外接圆半径为R,由3、4和6根长度为L的细杆和半径为r的圆环刚性连接组成,即组成三、四和六手性周期晶格。圆环和细杆的截面均为矩形,其宽度为b,高度为h。每根细杆和圆环的几何关系为相切。

图1 微尺度三、四和六手性周期晶格的单胞Fig.1 Unit cells of microscale hexachiral, tetrachiral and triachiral periodic lattices
1.2 考虑尺寸效应的有限单元法
基于修正耦合应力理论,微尺度欧拉梁的运动方程为[23-24]:
(1)
(2)
式中:E是杨氏模量;G是剪切模量;ρ是质量密度;A=bh是梁的横截面积;I=bh3/12是惯性矩;l0是修正耦合应力理论中的尺度参数;u和w分别表示梁的轴向和横向位移;f和q是轴向力和横向力。当尺度参数l0等于零时,运动方程可退化为基于经典理论的欧拉梁运动方程。
本文基于有限单元理论,采用2个节点和6个自由度来描述平面欧拉梁单元。局部坐标体系的欧拉梁的中性面的位移为:
(3)

(4)
式中l是欧拉梁单元的长度。因此考虑尺寸效应的微尺度欧拉梁的单元刚度和质量矩阵可以通过形函数计算:

(5)
式中:
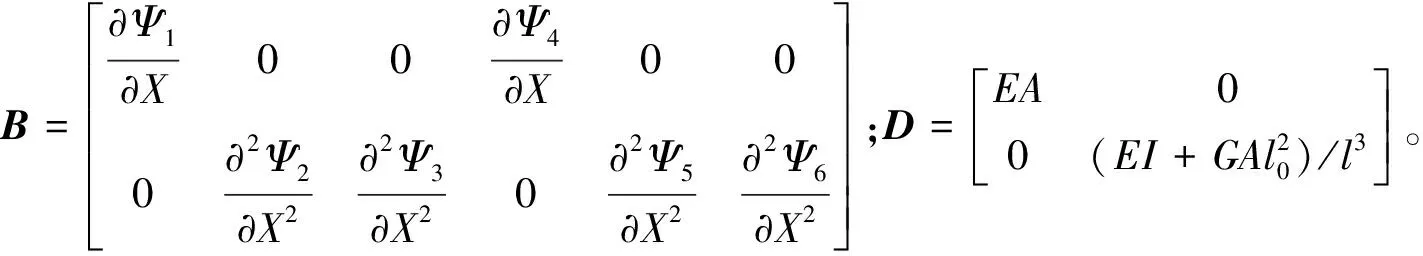
(Kg-ω2Mg)ug=0
(6)
式中:Mg和Kg是微手性晶格单胞的全局质量矩阵和刚度矩阵;ω是角频率;ug是所有节点的位移。
1.3 波传播分析
基于Bloch定理,周期晶格单胞中的任意节点位移可以通过相应的单胞的节点位移描述。通过应用Bloch定理,微尺寸周期晶格的运动控制方程为[25-27]:
(Kr(k1,k2)-ω2Mr(k1,k2))ur=0
(7)
式中:Kr(k1,k2)和Mr(k1,k2)是考虑周期性边界条件的刚度和质量矩阵;(k1,k2)是第一布里渊区的波矢。波矢沿第一不可约布里渊区的边界扫掠,并求解式(7)中的特征值,进而可以得到考虑尺寸效应的微尺度手性晶格的能带结构。
2 结果与讨论
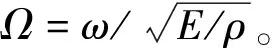
2.1 微尺度手性晶格的能带结构
如图2(a)所示为微尺度三手性晶格的能带结构其中几何参数α=0.86。与基于经典理论欧拉梁计算的能带结构相比,考虑尺寸效应的微尺度晶格的色散曲线分布在更高的频率中。这是因为在微尺度欧拉梁的运动方程中,尺寸效应增加了微尺度结构的弯曲刚度。经典理论计算的微尺度三手性晶格的前3条带隙分别为[2 222.67, 3 976.40]、[6 172.04, 8 121.93]和[8 791.51, 9 657.25],而考虑尺寸效应计算的前3条带隙分别为:[2 540.56, 4 343.17]、[7 010.08, 8 615.91]和[9 129.55, 10 608.57]。随着色散分支频率的增加,色散曲线与经典理论的计算结果偏离越来越远,2种理论计算出的带隙范围的差异增大。
如图2(b)所示,得到了几何参数α对带隙分布的影响。基于经典理论计算的带隙频率小于相应的考虑尺寸效应的带隙频率。区域的重叠区域表示2种理论所能计算的带隙范围,重叠面积越小,表示2种理论在微尺度结构计算时所产生的差异越大。同时,可以观察到,当几何参数α大于0.22时,带隙宽度逐渐降低。当几何参数α大于0.52时,最低频率的带隙宽度随着几何参数α的增大而增大。

图2 微尺度三手性周期晶格的能带结构和带隙分布Fig.2 Band structures and bandgap distributions of a microscale hexachiral periodic lattice
微尺度四手性晶格的能带结构(α=0.93)如图3(a)所示,考虑尺寸效应的色散曲线(实线)大于相应的基于经典理论计算的色散曲线(点线)。尺寸效应对前5阶色散曲线的形状影响较小。当考虑尺寸效应时,第5条色散曲线的最小值出现在M点,而经典理论计算的第5条色散曲线的最小值出现在X点,这表明尺寸效应不仅影响色散曲线的频率,还影响色散曲线的形状。图3(b)得到了几何参数对带隙分布的影响,考虑尺寸效应计算的带隙数量多于经典理论计算的带隙数量。这表明尺寸效应不仅影响带隙的频率和宽度,还影响带隙的产生。通过上述分析得到,为了准确描述微尺度手性晶格的带隙特性,必须考虑尺寸效应对微尺度晶格结构的动力学特性的影响。

图3 微尺度四手性周期晶格的能带结构和带隙分布Fig.3 Band structures and bandgap distributions of a microscale tetrachiral periodic lattice
微尺度六手性晶格(α= 0.93)的能带结构如图4(a)所示,考虑尺寸效应的色散曲线(实线)大于相应的基于经典理论计算的色散曲线(点线),表明尺寸效应对色散曲线的形状影响较小。显然,基于2种理论计算的能带结构中,只有一条带隙出现在第3和4条色散曲线之间。基于本文理论计算的带隙上限和下限出现在同一波矢处,而基于经典理论计算的带隙上限和下限对应的波矢则不同,这表明尺寸效应会使色散曲线的极值位置发生变化。图4(b)绘制了几何参数α对带隙分布的影响,基于经典理论计算的带隙频率小于相应的考虑尺寸效应计算的带隙分布。另外,考虑尺寸效应的计算结果,最高带隙在α为0.2附近产生间断,这可以用来调节带隙的打开或关闭,而经典理论计算的最高带隙则连续分布。
2.2 尺寸效应对色散表面的等频面的影响
本节使用色散表面的等频面来预测微尺度晶格结构中波传播的方向性,并研究尺寸效应对波传播方向性的影响。色散表面的等频面可以在特定频率下描述弹性波沿介质传播的各向同性或各向异性特征[29]。当等频面是圆形时,表明其在相应频率范围内的各向同性特性,而非规则几何形状如具有波瓣状的复杂等频轮廓表明其各向异性特性。

图4 微尺度六手性周期晶格的能带结构和带隙分布Fig.4 Band structures and bandgap distributions of a microscale trichiral periodic lattice
微尺度三手性晶格的前两阶色散表面的等频面如图5所示,图5(a)和(b)是采用经典理论计算的前两阶色散表面的等频面,(c)和(d)是考虑尺寸效应计算的等频面。如图5(a)所示,当频率小于612.5时,等频面是圆形,表明此频率下的弹性波在微尺度三手性晶格中的传播呈现各向同性特性。当频率大于612.5时,色散表面的等频面沿0°、±60°、±120°和180°方向出现向外突出的波瓣。图5(b)描述了微尺度三手性晶格第二阶色散表面的等频面,当频率小于918.5时,等频面为圆形,当频率大于918.5时,逐渐变为六边形,这表明随着频率的增大,弹性波传播的各向同性特性减小,各向异性增大。图5显示出了尺寸效应对微尺度三手性晶格的波传播的方向性具有重要的影响。在低频范围内,前2条色散表面的等频面是一个圆形,这表明弹性波的传播是各向同性的,弹性波均匀地向四周同时传播。随着频率的增加,第一阶色散表面的等频面由圆形变为具有“类六瓣形”(six-lobe)的复杂曲线,随着频率增大,这种现象表现得更为明显[30],这表示弹性波更易于沿高对称点方向传播。第二阶色散表面的等频面变为六边形,这表明微尺度三手性晶格的各向异性程度增加,弹性波在更高的频率下具有方向特性。

图5 微尺度三手性周期晶格的前两阶色散表面的等频面Fig.5 Iso-frequency surfaces of microscale hexachiral periodic lattice for the first and two dispersion surfaces
图6得到了微尺度四手性晶格的前两阶色散表面的等频面。
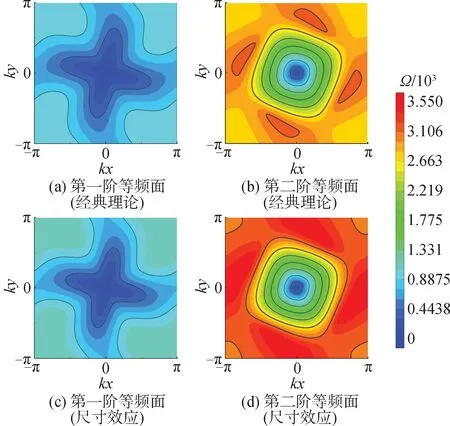
图6 微尺度四手性周期晶格的前两阶色散表面的等频面Fig.6 Iso-frequency surfaces of microscale tetrachiral periodic lattice for the first and two dispersion surfaces
如图6(a)和(c)所示,当频率小于449.8时,第一阶色散表面的等频面具有4个尖角,这表明四手性晶格较强的各向异性特性,这种强各向异性特性也出现在在宏观四手性晶中[26]。2种理论计算的第一阶色散表面的等频面都是具有4个尖角的复杂曲线,这表明微尺度四手性晶格具有较强的各向异性。随着频率的增加,等频面的尖角逐渐产生弯曲。低频范围内,第二阶色散表面的等频面是圆形。随着频率的增大,等频面由圆形转化为方形,进而转化为更为复杂的几何形状。从上述分析可知,尺寸效应增大色散曲面的等频面的频率,使色散面的等频面形状更加复杂,增加了该频率下弹性波传播的各项异性程度,即弹性波传播具有更强的方向特性。
3 结论
1) 尺寸效应对微尺度手性晶格中波传播特性具有显著的影响。尺寸效应影响色散曲线的频率和形状,导致带隙结构明显区别于经典理论计算的结果。
2) 通过前两色散面的等频面研究,得到了尺寸效应对微尺度手性晶格的波传播方向性的影响规律。研究结果证实了尺寸效应对微尺度晶格波传播特性的重要影响。

