正交异性钢桥面车轮横向位置识别

赵华，张斌，谭承君，张钰菲，郭泓捷

（1.湖南大学土木工程学院，湖南长沙 410082；2.风工程与桥梁工程湖南省重点实验室（湖南大学），湖南长沙 410082）

正交异性钢桥面板（Orthotropic Steel Decks，OSD）具有自重轻、极限承载能力强、施工周期短等诸多优点［1］，是钢桥、特大跨桥梁的首选桥面形式［2］.然而，OSD 在使用过程中普遍存在疲劳开裂现象［3］.为确保OSD 桥梁的使用安全，学者们逐渐开展了OSD 桥梁疲劳细节评估等相关研究工作［1］.Zhu 等［4］基于热点应力法对OSD 疲劳细节点的抗疲劳性能进行研究，并进行了疲劳寿命评估.为了提高OSD疲劳评估的精度，Cui 等［5］基于目标桥梁沿线道路上某路面动态称重系统（Weigh-In-Motion，WIM）所统计的实际车流数据（包括所有车辆轴重及总重）来进行疲劳相关分析.WIM 是一种动态测量移动车辆参数（速度、轴数、轴距、轴重及总重）的技术，一般通过埋置在路面下的压力传感器来实现［6］.虽然WIM 数据能够为OSD 的疲劳评估提供车流量、轴重等重要信息，但不能提供随机车流中每辆车经过目标桥梁的具体行驶车道.因此，利用WIM 数据来进行疲劳评估时一般假定随机车流中所有车辆其车道分布状况遵循一定的概率模型，这和实际情况有一定差异.

桥梁动态称重（Bridge Weigh-In-Motion，BWIM）技术直接利用桥梁为载体［7］，通过安装在主梁下缘的传感器来计算移动车辆轴重及总重，在中小跨径混凝土梁桥上有广泛的应用［8］.将BWIM系统应用于OSD桥梁，不仅能够用于监控超载车辆、获得上述WIM 所有数据，同时还能够掌握随机车流中每一辆车经过桥梁时所对应的行驶车道，这些具体信息将进一步提高OSD桥梁疲劳评估的精度.

目前BWIM 系统一般将桥梁视为一个单向整体梁单元，没有考虑到车辆（车轴）在某车道上的具体横向位置，而OSD 横向刚度弱，局部效应明显，其荷载响应对车轴横向位置非常敏感，若横向位置稍有偏差，则其疲劳细节应力幅以及相应的加劲肋响应信号将产生较大的差异，因此，准确掌握移动车辆过桥时的横向位置能够提高BWIM 系统车轴轴重识别精度［9］.同时，在OSD 桥梁疲劳寿命评估时，基于车轮荷载的横向分布所计算得到的等效应力幅明显小于基于最不利荷载位置所计算得到的等效应力幅［4］，若忽略过桥车辆的横向位置，则可能会高估桥梁的损伤度.为此，欧洲规范［10］和荷兰规范［11］等都给出了车辆轮迹线横向位置概率分布模型，显然，这些分布模型与实际情况有一定的差异.因此，基于BWIM 进行OSD 桥梁疲劳细节评估时，为提高其轴重识别和疲劳分析的准确性，掌握车辆在OSD 行驶的具体横向位置至关重要.

在BWIM 系统中，为获得移动车辆的具体横向位置，Quilligan［12］提出了二维BWIM 算法，利用桥梁影响面的概念识别车轮横向位置.张龙威［13］将这种方法推广到OSD 桥梁上，但是桥梁影响面在实际中难以准确获得，且计算耗时，难以在实桥中应用以获得实时数据.

此外，基于OSD 桥梁，Chen 等［14］利用轮载作用下三根纵肋响应间比值的变化拟合出了计算车轮横向位置的方程.这些方法虽然能够计算出车辆行驶过桥时的车轮横向位置，但是所拟合的方程系数的确定与OSD桥梁的具体细节构造（纵肋间距、纵肋尺寸、铺装层及钢板厚度）有着密切的联系.也就是说，当桥梁构造细节存在差异时仍需大量试验数据以重新拟合方程参数.Yu 等［15］将过桥车辆的车轴视为一个整体，基于最小二乘法计算出车辆过桥时的横向位置，并将该方法成功应用到普通混凝土简支T 梁桥.该方法虽然可以计算出车辆过桥时其车轮的横向位置，但是其中一个必要假设是假定车辆所有横向轴距均为固定值.由于OSD 桥梁较普通混凝土桥梁对过桥车辆车轮荷载横向位置更为敏感，当假设轴距为固定值时，所识别的车轮横向位置与实际情况会产生较大出入.并且，实际车辆横向轴距与假设的横向轴距差异越大，其横向位置识别误差就越大.因此，这些方法均不适用于随机车流在OSD 桥梁上行驶时其车轮横向位置识别.

本文将基于OSD 桥梁的横向影响线，利用BWIM 系统中的应变传感器（位于纵肋下缘）的响应信号来获取车轮经过桥梁时的具体横向位置.目前BWIM 技术一般基于Moses 算法，而Moses 算法需利用已知参数的车辆进行标定试验来获得桥梁的纵向影响线.且实际应用中，OSD的横向影响线难以通过现场试验获得.因此，本文提出的方法首先通过该标定试验建立一个高精度的OSD 有限元模型，随后利用该OSD 模型提取所需的横向影响线.本文通过建立基于横向影响线计算得到的纵肋下缘理论应变与实测应变之间的误差函数，利用最小二乘法，即通过计算误差函数的最小误差值来计算出车辆的实际车轮横向位置.为验证该方法的有效性和准确性，分别通过有限元数值分析以及现场试验进行了验证.

1 车轮横向位置求解方法

本文以三轴车为例，当其行驶经过OSD 时（见图1），其纵肋响应信号（应变）如图2 所示（仅列出车辆左轮正压位置附近三根肋）.

图1 车轮经过OSD时示意图Fig.1 Schematic of a vehicle passing over OSD

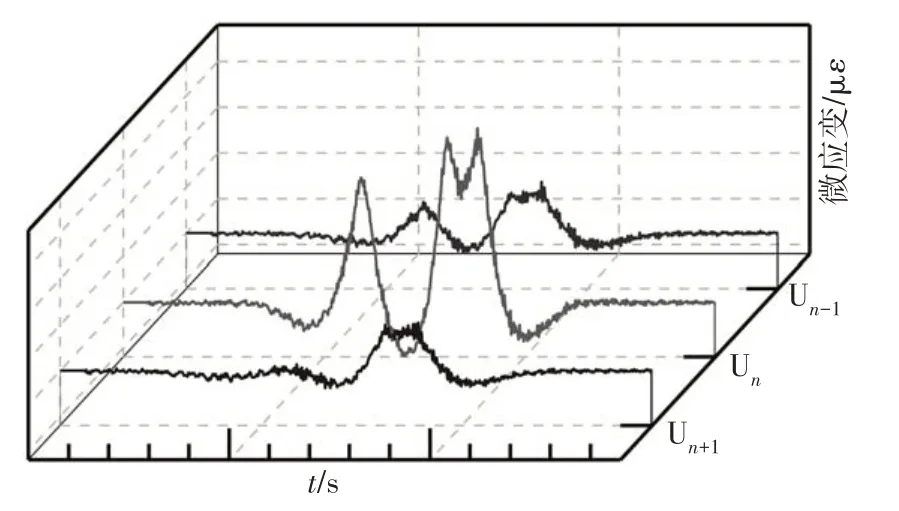
图2 纵肋响应信号示意图Fig.2 Schematic of the longitudinal rib response signal

首先，从这些实测信号中找出最大应变峰值及其对应U肋编号，假设该U肋编号为第#n纵肋.由于第#n纵肋位于或非常靠近车轮正压位置，如图2 所示，第#n纵肋的应变响应一般会显示出与车轴数对应的波峰信号，并且波峰所在时刻即为相应车轴经过此横断面的瞬间.

随后对每个车轴经过该测试断面的各个时刻，建立桥梁实测响应与预测响应之间的误差函数：

式中：a为相邻纵肋之间的距离；dl为车辆第l个车轴车轮荷载中心与最大应力所对应的第#n纵肋中线之间的距离（坐标轴方向定义为左负右正）.

值得一提的是，车轴与OSD 接触面积NS不是恒定值，比如最常见的3 轴货车，其第一个车轴只有一个轮子即N为1，而后两个车轴都是双排车轮即N为2.在随机车流中为了获得准确的N值，可以通过BWIM 系统中车轴探测传感器（Free of Axle Detector，FAD 传感器）识别的车辆车轴数量、轴距信息［7］与我国《公路货运车辆超限超载认定标准》对比来判定车轴横向的轮胎数量，从而确定具体的车轮数量.

最后可以控制公式（1）中的误差函数的最小值来求解车轮的横向位置d值.为了简化计算，可以通过假设一系列的d值，然后分别计算所对应的误差M值，相应的最小误差M值所对应的d值即为本方法求解的车轮横向位置.显然，本方法可以求解每一车轴经过OSD 测试断面的具体横向位置.图3 所示为本文提出的车轮横向位置识别方法的具体求解步骤.

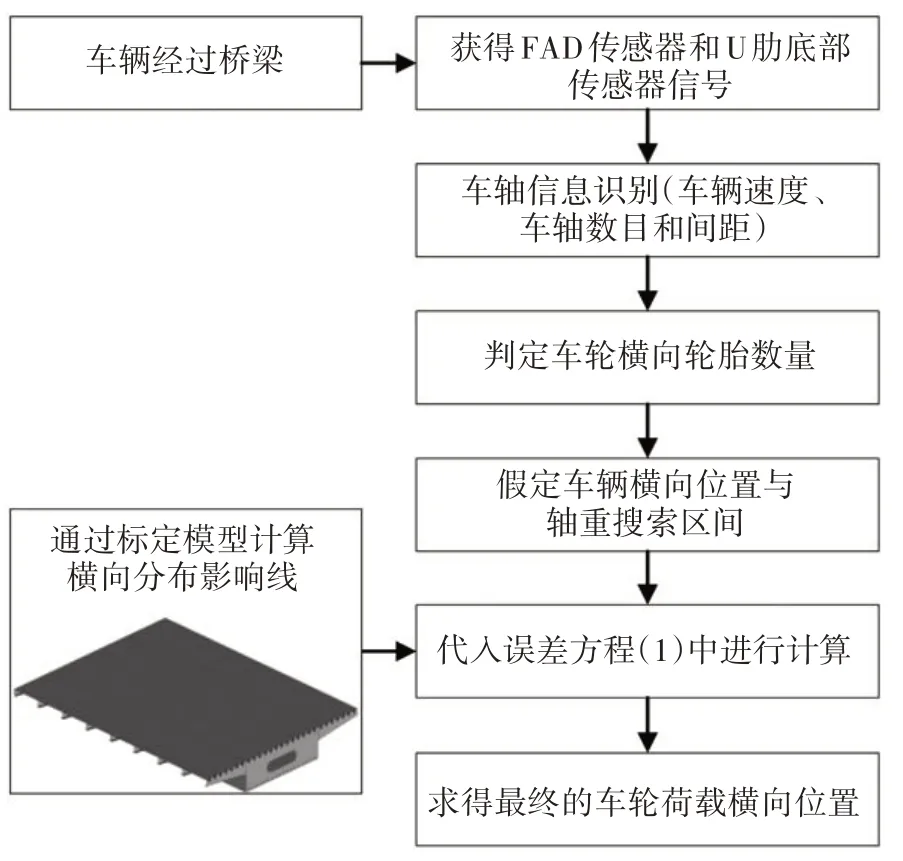
图3 车轮横向位置识别流程图Fig.3 Flow chart of the identification of transverse position of wheel loads

2 现场试验

试验桥梁（佛陈新桥）位于广东省佛山市.该桥主桥为一座三跨变截面连续钢箱梁桥，桥面采用OSD 形式，跨径布置为58.51 m+112.8 m+58.51 m.该桥共有两幅，单幅桥宽15.75 m.图4、图5 分别为测试桥梁总体立面图、标准横断面图.图6 示出了传感器平面布置图.本次试验测试区域位于其中一幅的主跨，距桥梁主跨一端支座24.4 m（如图4所示）.

图4 测试桥跨立面图（单位：m）Fig.4 Elevation of test bridge（unit：m）

如图5、图6 所示，试验中应变传感器安装于箱梁内部纵肋（#8～#20）的底部，并且相邻节段安装了两排车轴探测传感器（FAD 传感器），用于识别行驶车辆的速度、车轴数量以及车轴间距.其工作原理如下：根据FAD信号中波峰数量可以确定车轴数目，并利用一对FAD（沿纵向）信号峰值时间差来获得行驶车辆速度，最后根据车轴对应峰值时间差及速度可以获得车轴间距［7］.传感器均采用扬州科动公司生产的KD4001 工具式应变传感器.利用日本TML 公司生产的动态采集仪DC-204R 进行数据采集，采样频率为512 Hz.

图5 横断面图（单位：m）Fig.5 Cross section（unit：m）

图6 传感器平面布置图（单位：mm）Fig.6 Sensor layout（unit：mm）

此次试验测试车辆为1 辆3 轴车（总重约35 t），车辆具体参数如图7所示.试验3轴车包含1个前轴及1个组轴，其组轴中所包含的2个单轴的车轮横向间距相同，均为1 800 mm.试验中，车辆沿车道二匀速通过测试区域，由于场地限制（试验时桥梁仍处于施工中），试验车辆的目标速度设置为30 km/h 和40km/h，且每个速度重复通过测试区域3 次.如图8所示，当车辆行驶经过测试断面时，通过录像和桥面铺设的湿泥巴所显示的轮胎痕迹以及固定于桥面的钢尺来记录每一趟跑车的车轮具体横向位置.如图7所示，第二排车轴的车轮宽度及其横向间距与第三排车轴完全一致，而第一排车轴与其他两个车轴不同，为阐述方便，这里记（l=1～3）为第i个车轴左轮横向中心点与第k根纵肋中心点之间的距离，显然，试验跑车横向距离具体见表1.

表1 实际跑车情况Tab.1 Configuration of vehicle runs of field tests

图7 试验车辆参数（单位：mm）Fig.7 The test vehicle parameters（unit：mm）

图8 实际跑车图片Fig.8 The actual picture of vehicle

3 有限元模拟

本文利用Ls-dyna 软件，按Kwasniewski 等［16］提出的精细化车辆实体模型、桥梁实体模型和相互耦合模型建立车桥耦合全过程.

3.1 车辆模型

车辆的具体尺寸如图7 所示.图9（a）所示的三轴车模型是根据车辆技术图纸建立的.首先建立轮胎、前后悬架、车轴及车架等子系统实体模型，之后确定各个子系统之间的相对位置与连接方式，最后使用试错法修正模型的质量分布.

车辆悬架系统和车轮模型极大程度上影响了三轴车与桥梁的动力相互作用，因此它们是车辆模型中最重要的一环.车辆悬架系统主要采用1D 结构单元进行建模，通过在车辆悬架模型中引入铰链单元，实现车轮的3D 模型旋转功能.图9（b）显示了前悬架系统及其有限元模型，模型中为每个1D 单元建立了其对应的横截面面积和材料密度.

图9（c）展示了前轴轮胎有限元模型的建模全过程.胎体由2 层完全重合的壳单元组成，第一层用具有弹性材料属性的单元模拟橡胶，第二层使用Ls-dyna 中具有“fabric”材料属性的单元来模拟轮胎帘线，并向所有轮胎中施加内压.之后，更新车辆模型的材料属性、荷载和边界条件公式、接触算法等以完成最终的模型［16］.最后，通过移动货物的纵向位置将车辆有限元模型轴重与试验车静载轴重相匹配，最终配重结果如表2所示.

图9 车辆模型Fig.9 Vehicle model

表2 模拟车轴重分布Tab.2 Axle weights in Ls-dyna model

3.2 桥梁模型

桥梁模型如图9 所示，取纵向8 跨横隔板间距，共20 m 长.计算基于线弹性假设，钢板采用薄壳单元模拟，弹性模量为206 GPa，泊松比为0.3.钢箱梁节段模型使用两端固结的约束条件，并在所关注节段进行网格加密处理.

图9 桥梁节段有限元模型图Fig.9 FE model of the bridge segment

3.3 车桥耦合动力模型

基于上述车辆和桥梁实体模型，在Ls-dyna中两者采用点面接触的方式以防止模型穿透.在桥梁模型前后设置了刚性墙以作为车辆加速、驶入和驶出桥面的跑道.仿真分析中，车桥耦合的摩擦基于库仑摩擦公式实现，Ls-dyna 中设置静（FS）、动（FD）摩擦因数来激活.同时，由于接触关系和阻尼等因素的影响，车辆模型无法在桥梁节段内保持直线匀速行驶，故对车辆模型施加强制位移.最后赋予轮胎与车轴平动速度及旋转角速度以保证仿真分析更加符合实际情况.

图10 列出了工况1 的模拟结果，并与实际测量值进行了对比.当车辆沿车道二经过桥梁时，#13、#14 及#15 三根纵肋的响应最为明显，其模拟结果与实测响应趋势一致，整体差异不大.与工况1 类似，其他工况的理论结果与实测响应也吻合较好，进一步验证了桥梁有限元模型的准确性.

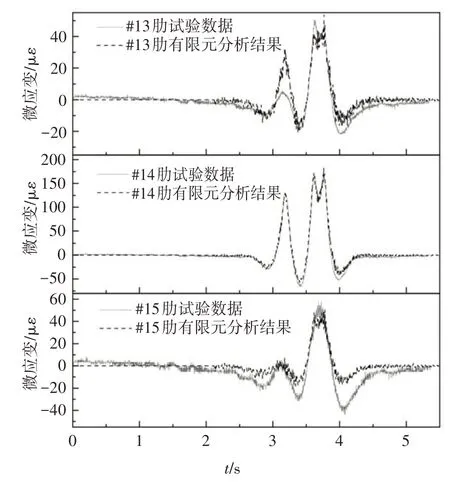
图10 工况1肋底纵向应变对比图Fig.10 Comparison of the longitudinal strains of ribs in case 1

3.4 横向影响线

根据上述建立的桥梁模型可获得各纵肋的横向影响线.以U14纵肋为例，将该纵肋中心位置记为原点，沿桥梁横向上从-1 278.5 mm 到1 278.5 mm，利用单位力进行加载（共33 次加载），根据其纵肋下缘响应信号来求得U14纵肋的横向影响线.参考Quilligan［12］中标定影响面的方法，采用三次样条曲线拟合，结果如图11 所示.值得一提的是，此次试验时，测试桥梁并未进行桥面铺装（在裸钢桥面上进行跑车试验），因此，相对于有桥面铺装的情况，该测试桥梁的横向刚度较弱.在铺设沥青层的情况下，桥梁的横向刚度将得到一定的提升.此外，图11中所指出的横向刚度变化段是相邻两纵肋的局部加强所致.

图11 U肋横向影响线Fig.11 U-rib transverse influence line

3.5 算法实例

以工况4 为例，首先利用Ls-dyna 模拟该工况，获得各U 肋下缘应变响应信号.不难发现纵肋U14的梁底响应最为显著，将其定为中心肋，同时发现纵肋U13的响应信号幅值比纵肋U15的响应信号幅值大，从而可以确定车轮中心位置位于纵肋U13、U14之间.因此，横向位置搜索区间可以设定为［-570 mm，0 mm］（570 mm 为纵向U 肋间距离），间隔为1 mm；轴重搜索区间设定为［4 t，15 t］，间隔为0.1 t.接触面积S取值为200 mm.仅选取纵肋U13、U14和U15相应的响应信号代入公式（1）进行计算.基于上述算法，该工况中第二个轴的误差函数计算结果如图12 所示，误差函数取最小值时其车轮横向位置为x214=-99 mm，实际值为-79 mm，误差为20 mm.

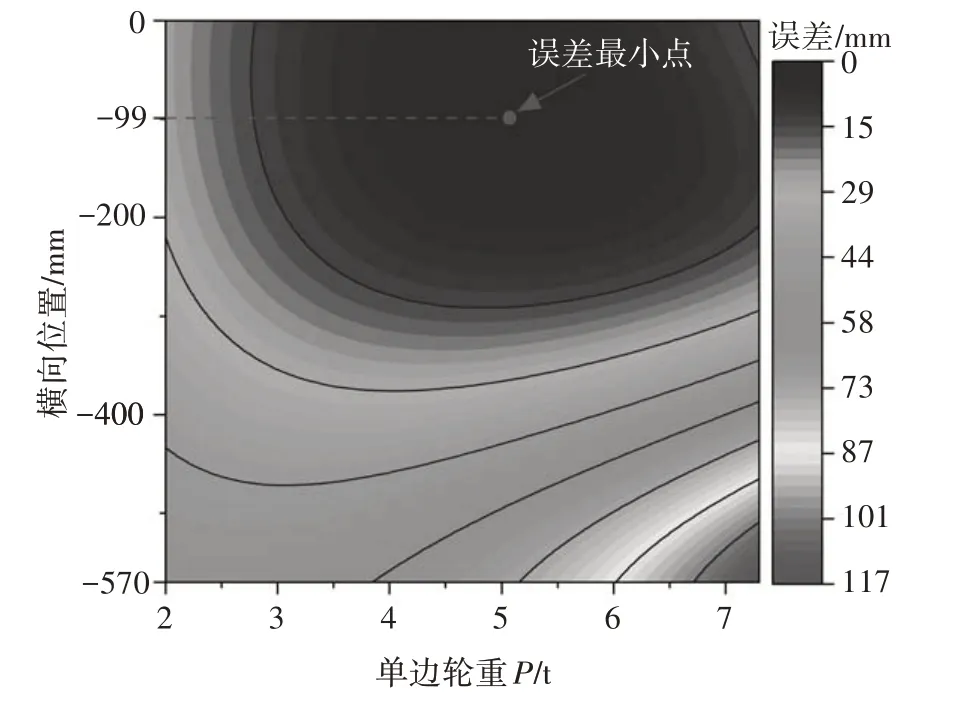
图12 工况4理论求解结果Fig.12 Results of the case 4 in FE model

4 参数分析

4.1 接触宽度S对识别精度的影响

上述分析中S取值为200 mm，而在实际情况中，车轮接触横向宽度受轮胎气压、载重重量、温度等多方面的影响，接触面积S可能有所不同.为了探究接触面积S对识别精度的影响，首先利用上述Ls-dyna车桥耦合模型模拟车辆左轮=0，且车速为30 km/h的跑车情况.利用上述方法以及不同S取值（从180到220 mm，间隔为10 mm）求解车轮横向位置.最终识别精度如图13 所示，中后轴识别结果的平均误差在9 mm 以内，所有轴识别结果的平均误差在2.3 mm以内，接触宽度引起的识别误差在19 mm 以内，当车轮接触宽度为200 mm 时，其误差平均值最小，因此，若无特别说明，则本文后续S均取值为200 mm.

图13 不同车桥接触宽度识别精度图Fig.13 Identification accuracy of different vehicle-to-bridge contact widths

4.2 车速对识别精度的影响

利用上述Ls-dyna 车桥耦合模型模拟车辆左轮=0，且车速分别为30 km/h、40 km/h、50 km/h 和60 km/h 的跑车工况.利用上述算法分别对该4 个工况进行车轮横向位置识别，结果如图14 所示.可以看出其横向位置识别精度整体较高，前轴横向位置的最大误差为29 mm，中后轴的最大误差为14 mm，中后轴识别结果的平均误差最大为12.5 mm，所有轴识别结果的平均误差最大仅为9 mm.由此可见，车速对于识别精度的影响较小.

图14 不同车速的识别结果Fig.14 Identification results with different vehicle speeds

4.3 不同横向位置对识别精度的影响

基于Ls-dyna所建立的车桥耦合模型，设定车速为60 km/h，分别模拟左轮=-285～285 mm（间隔124.5 mm）5 个跑车工况，如图15 所示.其识别结果如图16 所示.其中，不同横向位置引起的识别误差在29 mm以内，说明本文所提出的横向位置识别方法其识别精度受车轮所在具体横向位置的影响较小.

图15 车轮不同横向位置示意图Fig.15 Transverse locations for five different wheel positions

图16 不同横向位置识别结果Fig.16 Identification results with different axle transverse locations

4.4 不同车型(车轴数量)对识别精度的影响

为了进一步探究所提出的车轮横向位置识别方法的准确性及适用性，利用上述车辆模拟方法建立1辆五轴车模型，车辆的具体参数如图17 所示.该五轴车包含1 个前轴及2 个组轴，其中2 个组轴的车轮横向间距分别为1 840 mm 和1 880 mm.同样，利用Ls-dyna车桥耦合模型模拟该车辆左轮=0，且车速分别为30 km/h、40 km/h、50 km/h和60 km/h的4个跑车工况.图18记录了最终横向位置识别结果，其中，最大识别误差为28 mm，5 个轴的误差平均值最大仅为4.6 mm.由此可见，本文提出的车轮横向位置识别方法不受车辆类型（车轴数量、车辆长度等）限制.

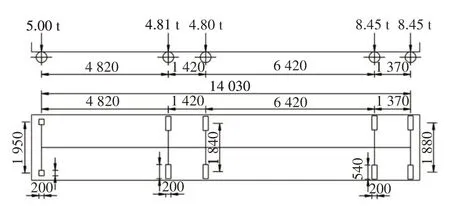
图17 五轴车示意图（单位：mm）Fig.17 Detail for five-axle vehicle（unit：mm）

图18 五轴车识别结果Fig.18 Results of the five-axle vehicle

5 实桥试验结果

基于上述纵肋横向影响线，按图3 所示求解流程，计算出实桥试验中6 个工况（表1）的横向位置，具体识别结果如表3所示.其中，前轴横向位置最大误差为131 mm，后两轴横向位置最大误差为71 mm，所有轴最大平均误差为71.3 mm.计算误差主要由以下3 个因素构成：1）对于试验三轴车，当某一车轴经过测试断面时，本文利用该测试断面相应的响应信号和标定的横向分布影响线单独识别该轴的横向位置，而该响应信号中没有考虑其他车轴的贡献（假定全部由该车轴经过测试断面产生），即认为各车轴之间无相互影响，但实际上过桥车辆不同车轴之间或多或少存在一定的相互影响；2）桥梁振动效应和测量噪声的影响；3）前轴重量相对较轻，其抗干扰（噪声、振动等）能力较差，误差相对大一些.考虑到无论在OSD 疲劳评估还是BWIM 系统中，较重车轴信息（后轴）才是更加值得关注的，因此，总体上，本文提出的车轮横向识别方法适用性较强，单个车轮的横向位置识别精度在工程范围内仍可以接受.

表3 实桥试验数据计算车轮荷载横向位置结果Tab.3 Calculation of wheel lateral position results from real bridge data mm

6 结论

基于OSD 桥梁的横向影响线和最小二乘法原理，本文提出了一种适用于OSD 桥梁的过桥车辆车轮横向位置识别算法.该算法仅需少量安装于纵肋底部的应变传感器和车轴探测传感器即可识别过桥车辆车轮的横向位置.本文通过有限元分析及实桥试验，对正交异性钢桥面车轮横向位置识别进行研究，主要结论如下：

1）基于Ls-dyna分别建立车辆、桥梁模型以及两者的耦合振动模型，通过实桥试验验证了有限元模型中桥梁模型的准确性，并获得了可靠的OSD 桥梁横向分布影响线.

2）有限元参数分析结果表明，所提出的适用于OSD 桥梁的过桥车辆横向位置识别方法，其车轮横向位置识别精度不受车轮接触宽度、车速、车辆横向位置及车辆类型的影响.整体来说，轴重越大的车轴其横向位置识别精度越高.

3）经过现场试验结果验证，本文所提出的过桥车辆横向位置识别算法操作简单，且具有极强的鲁棒性，能够提高BWIM 系统轴重识别精度和OSD 桥梁的疲劳损伤评估准确度.

此外，该算法也存在着不足，需要通过建立OSD桥梁的高精度模型以提取出准确的横向影响线，并且多车过桥时的横向位置识别仍然是该算法的主要困难.另外，传统正交异性钢桥面结构可能出现局部损伤，影响其横向影响线，因此，该方法在实际使用中可能需要定期对目标桥梁进行模型修正.