龙卷风作用下大跨度桥梁车-轨-桥耦合振动及行车安全性
张迅,王力东†,韩艳,朱志辉,蔡春声,何旭辉
(1.长沙理工大学土木工程学院,湖南长沙 410114;2.中南大学土木工程学院,湖南长沙 410075;3.东南大学交通学院,江苏南京 211189)
龙卷风是由雷暴等中尺度对流天气系统引发的微尺度强对流极端天气,具有很强的破坏性.据统计,我国每年发生龙卷风达百次左右[1].虽然到目前为止国内还没有出现由龙卷风引发的列车行车安全事故,但在世界范围内已有此类事故报道.如铁路网同样发达的日本,分别在2005年和2006年发生过龙卷风致列车脱轨事故,共造成5 人死亡、近40 人受伤.另一方面,为保障高铁线路的平顺性,我国建造了许多大跨度桥梁[2-3],致使桥上列车遭受龙卷风作用的概率大大增加.因此,开展龙卷风作用下大跨度桥梁车-轨-桥耦合振动及行车安全分析具有重要现实意义.
目前,国内外已有学者开展了相关研究.陈艾荣等[4]根据Kou-wen 提出的龙卷风三维理论模型,采用准定常理论研究了移动龙卷风作用下大跨径桥梁的动力响应,发现竖向风作用下桥梁表现出强烈的托起效应.Cao等[5]通过刚性模型测压试验测试了大跨度桥梁流线型桥面在龙卷风作用下的表面压力,分析了涡流比和旋涡中心到桥面距离对表面压力和气动力系数的影响.张寒等[1]以Ward 型龙卷风发生装置为原型,通过建立相应CFD 数值模型,研究了龙卷风作用下高铁连续梁桥结构表面风压的分布规律.Suzuki 和Okura[6]基于自主研发的实验装置,测试了列车穿过龙卷风模拟器时表面的非定常压力.随后,Obara 等[7]通过建立与试验条件相同的数值模型,在验证模型有效的基础上进一步揭示了列车穿过涡流时流场的变化.Xu 等[8]对高速列车与类龙卷风涡旋的相互作用进行了数值模拟研究,发现当列车速度为160~250 km/h 时,脱轨系数和倾覆系数达到最大值.Baker和Sterling[9]基于其前期推导的龙卷风风速场理论模型[10],结合边界层风洞试验获取的气动力系数,提出了一种移动龙卷风作用下列车行车安全评估方法,该方法考虑了风荷载的准静态和动态效应.以上研究主要针对龙卷风作用下桥梁[1,4,11]或列车[6-8,10]开展研究.对于车桥系统,操金鑫等[12]利用龙卷风模拟器研究了高架桥上静止列车表面风压分布规律.潘宝[13]结合CFD 数值模拟方法和车-桥耦合振动理论,对龙卷风作用下桥上高速列车的气动特性和运行安全性进行了评估,探讨了列车距涡核距离、风速和车速对行车安全性的影响.该研究考虑列车在简支梁桥上行车,对于龙卷风作用下大跨度桥上车-轨-桥耦合振动的研究有待进一步开展.
本文以某公路铁路两用跨海斜拉桥为研究对象,采用Kou-wen 三维半经验公式模拟龙卷风风速场,并根据准定常理论计算桥梁和列车风荷载时程.在此基础上,考虑轮轨空间非线性接触,建立龙卷风作用下车-轨-桥耦合振动模型.数值算例中,以CRH2型动车组通过该桥为例,在风洞试验和CFD数值模拟获取车辆和桥梁气动力系数的基础上,探讨龙卷风强度等级、移动路径和车速对车-桥系统动力响应及行车安全性的影响,得出相关结论.
1 龙卷风对桥梁和列车的作用模式
1.1 龙卷风风场模拟
龙卷风风场结构非常复杂,呈水平移动的三维漏斗状涡流结构,包含切向、径向、竖向和平移风速.Kou-wen 龙卷风模型考虑了三维龙卷风风场,广泛应用于桥梁和建筑结构分析[14].因此,本文采用该模型建立龙卷风风速场.
Kou-wen 模型根据边界层将龙卷风在空间上分为内、外两部分,其边界层厚度表达式为:

式中:r=r′/rmax表示归一化半径,r′为模拟点距龙卷风中心的距离,rmax为最大切向风速对应的半径;δ0表示r≫rmax位置处的边界层厚度.
边界层外(η>1)风速为:
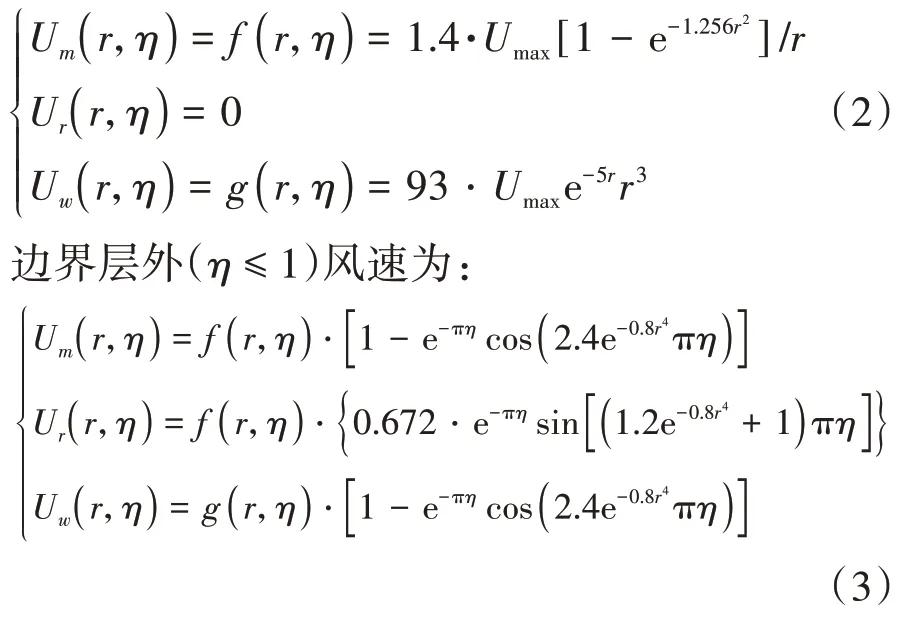
式中:Um、Ur和Uw分别表示龙卷风在极坐标系下的切向、径向和竖向风速;η=z/δ(r)表示归一化高度,z表示模拟点的离地高度;Umax表示最大切向风速.参考文献[15],龙卷风平移风速Vw可通过最大切向风速Umax确定:

1.2 桥梁和列车风场
本文考虑列车通过桥梁时遭受移动龙卷风作用.由于列车和龙卷风同时移动时,龙卷风对列车和桥梁的作用模式难以穷尽,因此,本文假设龙卷风由列车右侧平移至左侧,且龙卷风中心和列车组中间位置恰好在桥梁跨中相遇.同时为方便后续描述龙卷风移动路径,规定龙卷风移动路径与列车行驶方向的夹角为ψ.图1所示为移动龙卷风作用下桥梁节点风速计算简图,图2 所示为车辆通过移动龙卷风简图.图中Vv为列车行驶速度,Lv0和Lw0分别表示0时刻车辆质心和龙卷风中心距桥梁跨中的距离,且Lv0和Lw0存在Lw0=(Lv0/Vv-t)·Vw的关系.

图1 桥梁节点风速计算简图Fig.1 Wind speed of bridge node

图2 移动车辆风速计算简图Fig.2 Vehicle moving through a tornado
计算风荷载之前必须得到直角坐标系下桥梁和车辆的风速.根据图1 和图2 所示几何关系,桥梁节点或车辆质心处风速计算公式如下:
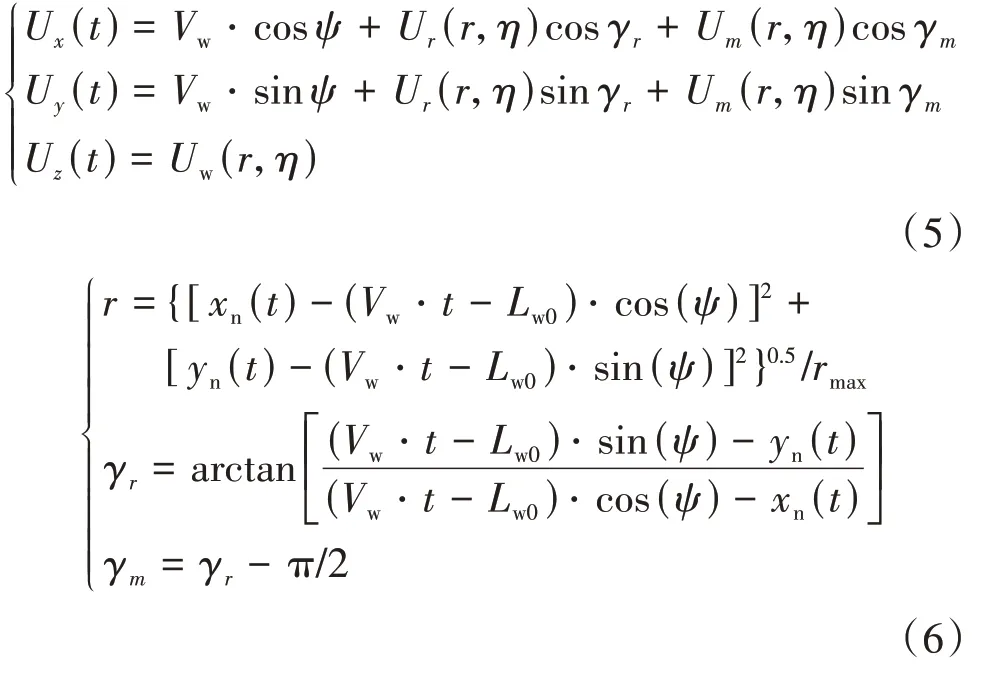
式中:Ux、Uy和Uz分别表示龙卷风作用下桥梁节点或车辆质心处的顺桥向风速、横桥向风速和竖向风速;γr和γm分别表示桥梁节点或车辆质心处龙卷风径向风速和切向风速与列车行驶方向的夹角;r表示桥梁节点或车辆质心距龙卷风中心的归一化距离;(xn,yn)表示桥梁节点或车辆质心的坐标.
1.3 桥梁和列车气动力荷载
由于龙卷风局部风速大,作用时间短,因此仅考虑平均风的作用[4,9-10,14].根据准定常理论,龙卷风作用下桥梁风荷载表达式为[10]:
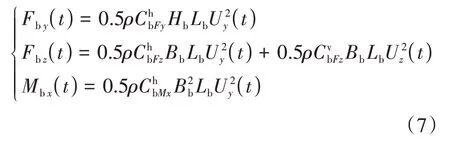
式中:Fby、Fbz和Mbx分别表示桥梁受到的阻力、升力和力矩;Cb表示桥梁的气动力系数,这些气动力系数可通过风洞试验或CFD 数值模拟获得,其中上标h和v分别表示横桥向风和竖向风,下标F和M分别表示力和力矩,x、y和z分别表示力和力矩的方向;Hb和Bb分别表示桥梁的高度和宽度;Lb表示桥梁风荷载节点的间距;ρ表示空气密度,取1.255 kg/m3.
龙卷风作用下列车风荷载表达式为:

2 龙卷风作用下车-轨-桥耦合振动方程
车-轨-桥耦合振动系统包含车辆子系统和轨道-桥梁子系统.车辆子系统采用多体动力学模拟,每节车辆包含1 个车体、2 个转向架和4 个轮对.其中车体和转向架包括横移、浮沉、侧滚、摇头和点头运动;轮对包括横移、浮沉、侧滚和摇头运动,单节车辆总计31个自由度(见图3).轨道-桥梁子系统采用有限元方法模拟.当考虑龙卷风作用时,车-轨-桥耦合振动方程可以表示为如下形式:
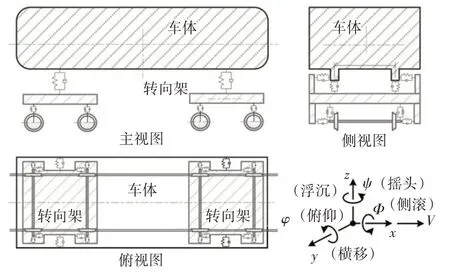
图3 车辆模型Fig.3 Vehicle model

式中:M、C和K分别表示车辆或桥梁子系统的质量、刚度和阻尼矩阵;U、和分别表示车辆或桥梁子系统的位移、速度和加速度向量;下标v 和b 分别表示车辆子系统和桥梁子系统;Fbw和Fvw分别表示桥梁和车辆所受龙卷风荷载;Fvb和Fbv表示轮轨接触力.
桥梁和车辆所受龙卷风荷载Fbw和Fvw可由第1节所述方法求解.对于轮轨接触力Fvb和Fbv的求解,需要先利用空间迹线法确定轮轨接触点位置,再根据赫兹非线性理论计算轮轨法向力以及结合Kalker线性蠕滑理论和Johnsin-Vermeulen 非线性理论计算蠕滑力[17].最后,采用分离迭代法求解式(9)所示耦合系统动力方程.
3 数值算例
3.1 工程背景
本文以8 车编组(1 拖+2 动+2 拖+2 动+1 拖)CRH2 型高速列车组通过某4 塔跨海斜拉桥为例,分析移动龙卷风对桥梁和列车动力响应以及列车行车安全性的影响.车辆参数参考文献[18],桥梁整体布置和主梁的截面形式如图4所示.主桥全长1 371.8 m,采用(58.5+116+3×340+116+58.5)m 的桥跨布置形式.桥面宽度达49.6 m,截面中心布置双线铁路,两侧布置三车道公路.铁路两侧布置透风率为40%、高度为2.75 m的风屏障.

图4 桥梁整体布置和主梁的截面形式Fig.4 General layout of bridge and section of main beam

利用ANSYS 建立轨道-桥梁有限元模型.桥梁结构阻尼比取0.5%.基于子空间迭代法获取桥梁前10 阶自振频率和振型(见表1).可以看出,桥梁前10阶自振频率均在1 Hz 以下,且相邻振型之间频率接近,这与大跨度斜拉桥的长周期动力特征相符.

表1 桥梁自振频率及振型Tab.1 Natural frequency and mode shape of the bridge model
3.2 桥梁和列车气动力系数
横桥向风和竖向风作用下车辆和桥梁的气动力系数是计算龙卷风荷载的重要参数.本文通过风洞试验确定横桥向风作用下车辆和桥梁的气动力系数.由于桥梁模型较宽,考虑到阻塞率和试验安全的要求,无法开展竖向风作用下的气动力风洞试验.因此,本文通过CFD 数值模拟获得竖向风作用下车辆和桥梁的气动力系数.风洞试验所用车-桥系统模型如图5 所示,其中桥梁采用缩尺比为1∶43 的节段模型,列车采用包含一节头车和一节中间车的同缩尺比模型.车辆模型高度还原了实际车辆的几何外形.由于列车组头车和尾车外形相同,因此头车模型气动力系数亦作为尾车气动力系数.车辆和桥梁的气动力分别采用测压法和测力法获取.试验前将两个三分量应变天平分别固定于风洞顶板和风洞底板上,桥梁节段模型固定于两天平中间.列车模型的尾部固定在下端板上,测压模块放置在下端板外,模型的底部与桥面分离,并用垫块支撑在桥面上.列车模型表面共布置测压截面20个,测压孔438个.试验在10.6 m/s的均匀流场中进行,利用天平测量桥梁模型的力和力矩,利用美国PSI电子扫描阀测量列车模型表面压力分布,利用眼镜蛇测量参考点风速.测力所用应变天平和测压所用PSI 电子扫描阀设置相同的采样参数,采样时间为30 s,采样频率为330 Hz.

图5 试验模型(单位:mm)Fig.5 Test model(unit:mm)
图6 给出了横桥向风作用下车辆通常段各截面的风压系数分布和头车各截面的风力系数.通过图6(a)可以看出,通常段各截面的风压分布基本相同.迎风区的风压系数大于尾流区,这是风荷载对列车产生阻力的重要原因.通过图6(b)可以看出,车辆渐变段的阻力和升力小于通常段,同时,在距车头100 m 位置处,升力出现了减小的现象,这可能是由于该位置处列车顶面变化较大的原因.侧滚力矩系数在渐变段和通常段交界处发生了变号.将风压系数对列车表面积分得到列车整体气动力系数,具体细节见文献[12].
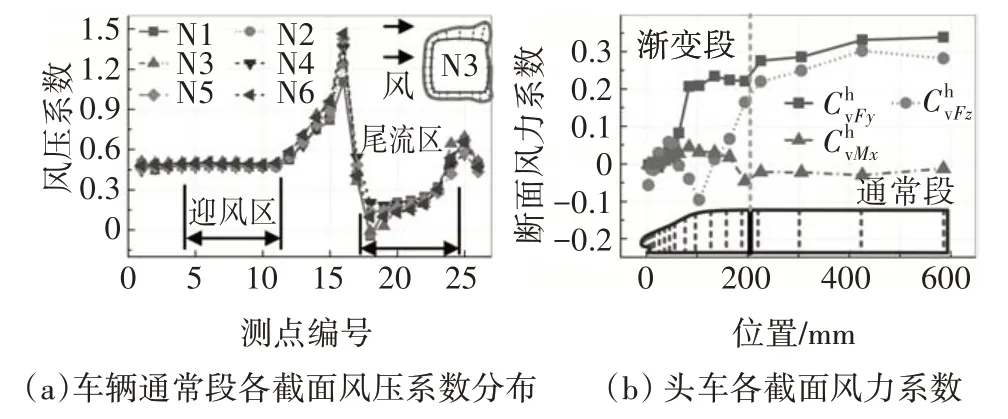
图6 截面风压分布和截面风力系数Fig.6 Pressures comparison and force coefficients of sections
本文采用CFD 数值模拟确定竖向风作用下列车和桥梁气动力系数.图7(a)为竖向风作用下车-桥系统的三维流场分析模型.该模型计算域长18.67 m、宽2.33 m、高11.67 m,模型尺寸和来流风速与风洞试验相同.计算域的底面设置为入口边界,即VELOCITY-INLET 速度入口;顶面设置为压力出口,即PRESSURE-OUTLET 出口边界,同时将出口静压设置为0 Pa.列车、桥梁表面设置为无滑移固体壁面边界条件;计算域的侧面设置为对称边界条件.为保证计算精度,计算域网格中车辆和桥梁均采用结构化网格进行离散.图7(b)给出了竖向风作用下车-桥系统周围的压力分布.可以看出,竖向风受宽幅桥面阻挡,下部为正压区,上部为负压区,因此竖向风作用下桥梁的升力系数较大.
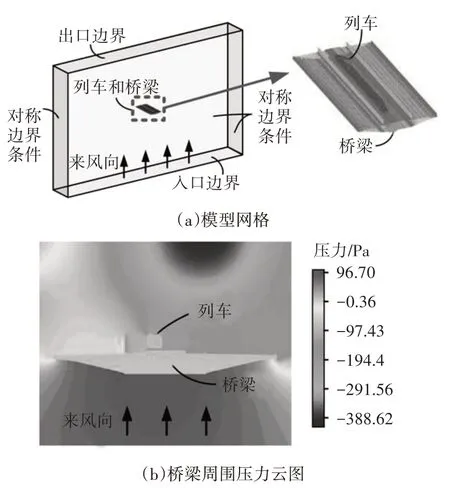
图7 车-桥系统CFD三维分析模型Fig.7 3D CFD analysis model of vehicle-bridge system
通过风洞试验和CFD 数值模拟确定的横桥向风和竖向风作用下车辆和桥梁的气动力系数见表2.
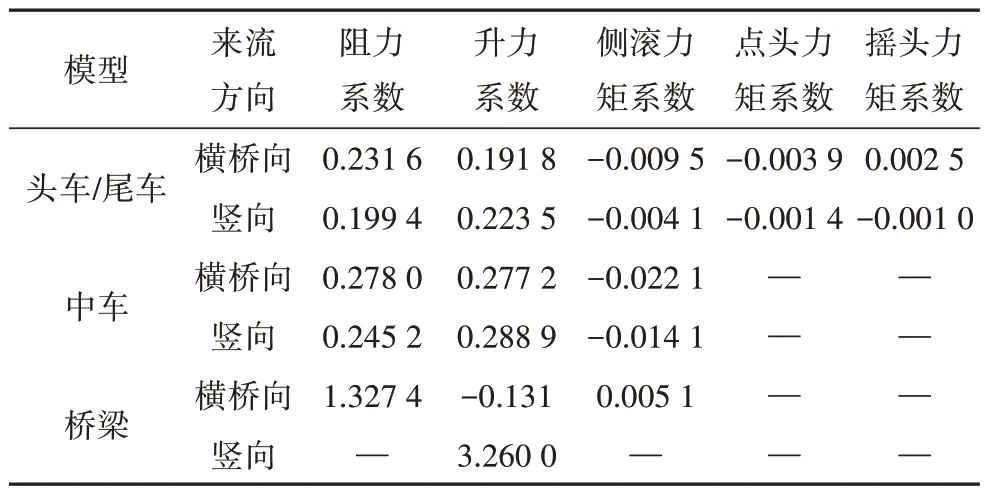
表2 车辆和桥梁气动力系数Tab.2 Aerodynamic coefficients of trains and bridges
3.3 桥梁和列车风荷载时程
综合考虑沿海地区各强度等级龙卷风发生的频率和伴生破坏能力[19],本文选择EF1级和EF1.3级龙卷风进行研究.表3给出了EF1和EF1.3级龙卷风的特征参数值.根据式(2)~(6)得到桥梁节点和车辆的风速时程,进而通过式(7)和(8)得到相应的风荷载时程.
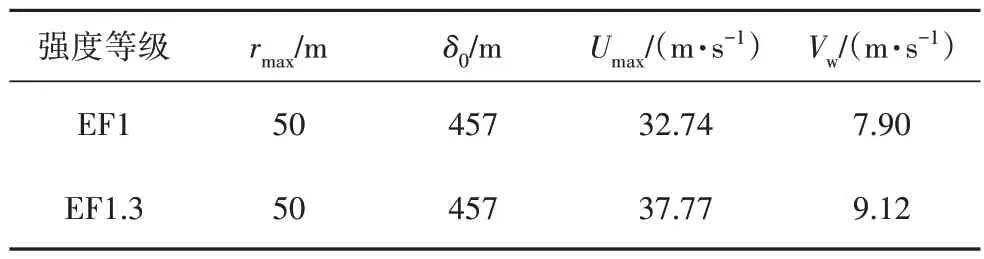
表3 龙卷风特征参数值Tab.3 Basic parameters of tornado
图8 给出了车速为150 km/h,ψ=90°时桥梁节点和车辆的风荷载时程曲线.其中节点A表示桥梁第二跨跨中,节点B和C表示距离跨中rmax=50 m 位置[如图4(a)所示].通过图8(a)~(c)可以看出,由于龙卷风的移动特性,节点C的阻力和力矩幅值大于节点B;同时,节点A的升力远大于节点B和C,这与文献[4]的结论相同.通过图8(d)~(f)可以看出,车辆的阻力、升力和侧滚力矩曲线形状相似,均包含两个峰值,且第一个峰值明显大于第二个.产生该现象的原因是由于龙卷风为三维漩涡结构,车辆通过龙卷风时,横桥向风速方向发生了变化,而竖向风速方向未变化.在横桥向和竖向风荷载叠加后,出现了前一个峰值大于第二个的现象.

图8 桥梁跨中和车辆风荷载时程Fig.8 Wind loading history of bridge midspan and vehicles
3.4 动力响应分析
3.4.1 桥梁动力响应
本节对EF1 级龙卷风作用下车-桥系统动力响应进行分析.龙卷风移动路径ψ选定30°、60°、90°、120°和150°,行车速度选定90 km/h、120 km/h、150 km/h、180 km/h 和210 km/h.图9 给出了不同车速下桥梁第二跨跨中位移和加速度最大值随龙卷风移动路径ψ的变化规律.可以看出,当龙卷风移动路径ψ在60°~120°之间时,桥梁竖向位移和加速度相对较大.以车速210 km/h 为例,龙卷风移动路径从30°变为90°时,第二跨跨中竖向位移和加速度分别从227 mm、182 mm/s2增加至309 mm、346 mm/s2.相比之下,龙卷风移动路径对横向位移和加速度的影响并未表现出明显规律.当龙卷风移动路径不变时,车速对桥梁横向和竖向振动响应影响规律不明显.比如龙卷风移动路径为90°时,第二跨跨中竖向位移以车速210 km/h 时最大,车速120 km/h 时次之,车速150 km/h时最小.该现象表明,当同时考虑列车和龙卷风作用时,桥梁动力行为变得更为复杂.
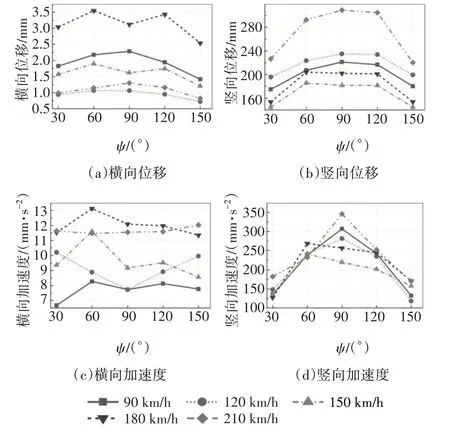
图9 第二跨跨中动力响应最大值Fig.9 The maximum dynamic responses of bridge midspan
图10 给出了EF1 级龙卷风作用下,列车以150 km/h 通过桥梁时第二跨跨中的振动响应时程曲线.由图10(b)可以看出,由于竖向风对主梁有托起作用,第二跨跨中竖向位移总体呈现上移趋势,在竖向风速最大时桥梁竖向位移最大.这说明桥梁竖向最大竖向位移主要是由竖向风引起的.由于本文假设龙卷风中心和列车组中间位置恰好在桥梁第二跨跨中相遇,因此,当桥梁竖向风速最大时,不同车速的列车距第二跨跨中的距离也不同.以车速210 km/h 为例,当跨中竖向风速第一次达到最大值时(t=15.01 s),车头驶离2 号桥塔62.3 m,距第二跨跨中107.67 m.此时,由于列车距第二跨跨中较远,导致竖向风对桥梁的托起作用最为明显.这可能是车速为210 km/h 时桥梁竖向位移最大的原因[见图9(b)].对于其他车速,在t=15.01 s时,车头距第二跨跨中的距离较短,列车振动对跨中的影响较为复杂,导致跨中竖向位移随车速变化的规律不明显.以上现象说明与列车竖向荷载相比,竖向风产生的托起作用对桥梁影响更大,故在对龙卷风作用下桥梁动力响应研究中,不能仅考虑龙卷风的平面漩涡.从图10(c)和10(d)可以看出,由于列车荷载的作用,在列车位于第二跨跨中位置时,桥梁产生明显的高频振动,此时桥梁横向加速度最大;桥梁跨中竖向加速度受列车荷载和龙卷风共同作用,当ψ在60°~120°时,龙卷风引起的作用更显著,使得加速度最大值不一定出现在列车位于跨中位置时.

图10 桥梁跨中动力响应时程Fig.10 Dynamic response time history of bridge midspan
3.4.2 车辆动力响应
图11 给出了EF1 级龙卷风作用下,列车以150 km/h 通过桥梁时,车体动力响应最大值随龙卷风移动路径ψ的变化规律.其中第1 节车为头车,第8 节车为尾车.由图11(a)和图11(c)可看出,尾车的横向位移和加速度最大,并且由头车至尾车,车体横向位移逐渐增大,在龙卷风沿ψ=60°方向移动时,车体横向位移随车辆节数的变化最为显著,尾车最大横向位移较头车增加30%.由图11(b)和图11(d)可看出,头车和尾车的竖向位移较大,中车的竖向加速度较大.
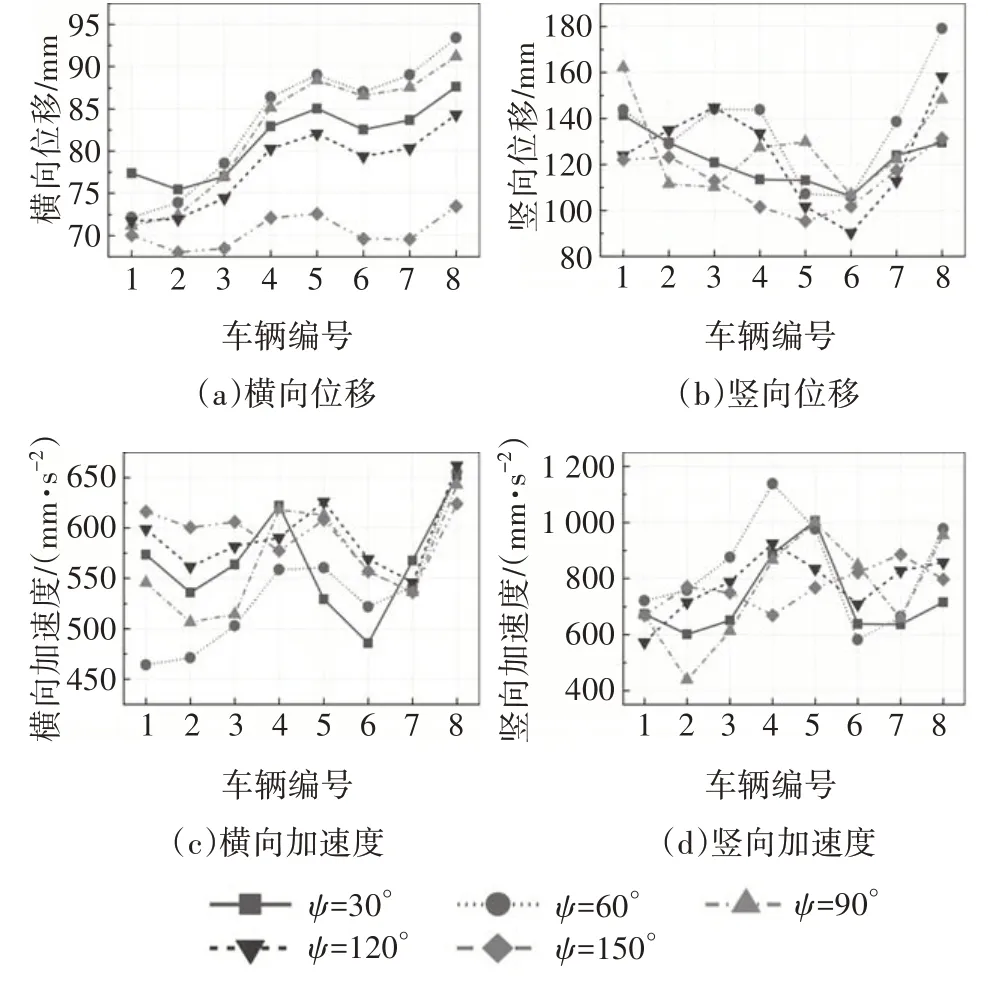
图11 列车动力响应最大值Fig.11 The maximum dynamic responses of vehicle
图12 为上述工况下第4 节车和第8 节车的动力响应时程曲线.从图中可看出,除竖向位移外,第4节车和第8 节车的其余动力响应变化趋势基本一致.竖向位移的差别主要是由第4节车和第8节车通过第二跨跨中附近时桥梁的竖向位移不同引起的[见图10(b)].对比图10(b)和图12(b)可以看出,当车辆经过风荷载最大位置时,桥梁竖向位移较小而车体的竖向位移达到最大值,并且车体竖向位移的方向向上.表明该时刻车体和桥面的相对位移最大,车辆行车安全性较差.车辆的横向位移在风荷载最大位置附近达到最大值,之后随着车辆驶离风荷载最大位置,横向位移逐渐趋于平稳.车体的横向和竖向加速度变化趋势类似,在车辆风荷载达到最大值前逐渐增加,达到最大值后迅速减小并达到反向的最大值,且反向加速度的最大值更大.因此,要重点关注车辆风荷载突然减小时车辆的行车安全.对比图8 和图12 可看出,虽然龙卷风作用下车辆受到的阻力和升力大小接近,但车体竖向动力响应明显大于横向,表明车辆动力响应受龙卷风荷载和桥梁动力响应的共同影响.

图12 车辆动力响应时程Fig.12 Dynamic response time history of vehicles
3.5 列车行车安全性分析
3.5.1 轮重减载率、脱轨系数和轮轴横向力
轮重减载率、脱轨系数和轮轴横向力是评判列车行车安全性的重要指标[20].图13 给出了车速为150 km/h,ψ=90°,龙卷风等级为EF1 级时,第4节车第3 个轮对的轮重减载率、脱轨系数和轮轴横向力时程曲线.从图13 中可以看出,在车辆所受风荷载最大位置,轮重减载率变化较小,而脱轨系数和轮轴横向力显著增加并达到最大值.同时,由于计算时规定龙卷风从列车右侧移动到左侧,导致车辆有向左侧移动和倾覆的趋势,故左侧车轮的脱轨系数略大于右侧车轮.
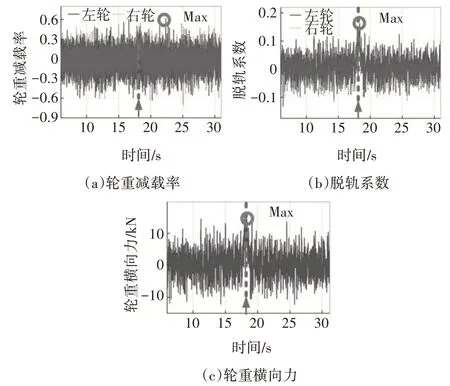
图13 第4节车行车安全指标时程曲线Fig.13 Time history curve of running safety indexes of the fourth vehicle
图14 给出了车速为150 km/h 时,各节车辆的轮重减载率、脱轨系数和轮轴横向力最大值随龙卷风移动路径ψ的变化规律.从图14 中可以看出,拖车的轮重减载率和脱轨系数大于动车.当龙卷风移动路径ψ<90°时,中间车辆(第4、5 节车)的轮重减载率最大;当ψ≥90°时,尾车(第8节车)的轮重减载率最大.对比图14(b)和图14(c)可以看出,脱轨系数和轮轴横向力的分布规律类似.并且,当ψ=150°时,列车组脱轨系数整体偏小,其余移动路径下尾车的脱轨系数最大.

图14 各节车行车安全指标最大值Fig.14 Maximum value of train running safety indexes
3.5.2 安全行驶范围
为分析龙卷风作用下列车能够安全通过桥梁的条件,图15 给出了EF1 级和EF1.3 级龙卷风作用下,列车轮重减载率、脱轨系数和轮轴横向力最大值随龙卷风移动路径ψ和车速的变化规律.可以看出,轮重减载率随车速提高呈增大趋势.龙卷风移动路径ψ对脱轨系数和轮轴横向力影响显著,当ψ在60°~90°时,脱轨系数和轮轴横向力较大;当ψ=150°时,行车安全性指标最小.依据现行规范[20],要求车辆轮重减载率≤0.8,脱轨系数≤0.8,轮轴横向力≤15+P0/3,其中P0为静轴重.从图15中可以看出,轮重减载率最容易超过规范限值,其次是脱轨系数和轮轴横向力.EF1 级和EF1.3 级龙卷风作用下,轮重减载率分别在车速达到180 km/h 和114 km/h 时超过规范限值.EF1 级龙卷风作用下,计算车速范围内脱轨系数和轮轴横向力均未超过规范限值;EF1.3级龙卷风作用下,脱轨系数和轮轴横向力分别在车速达到164 km/h和159 km/h时超过规范限值.
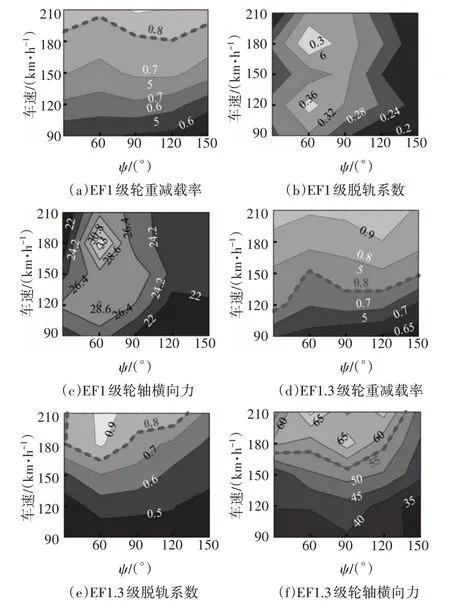
图15 行车安全指标最大值Fig.15 Maximum value of running safety index
表4 给出了车速为210 km/h 时,列车组行车安全指标最大值出现位置.可以看出,轮重减载率最大值出现在右轮,脱轨系数最大值出现在左轮.同时,由于拖车质量相对动车较轻,安全性指标较大,故增加车辆质量对行车安全有益.当龙卷风移动路径ψ≥90°时,尾部车辆的轮重减载率最大;当ψ<90°时,中部车辆的轮重减载率最大,这与3.5.1 节的结论一致.因此对于龙卷风中心与列车组中间位置相遇的情况,需要重点关注列车组中部和尾部车辆的行驶安全性.

表4 行车安全性最大值对应位置Tab.4 Position of maximum running safety
4 结论
本文以移动龙卷风作用下CRH2 型高速列车组通过某4 塔跨海斜拉桥为例,基于准定常理论计算了龙卷风作用下桥梁和列车风荷载,并将其与车-轨-桥耦合振动模型相结合,研究了龙卷风强度等级、移动路径和车速对桥梁、车辆动力响应及行车安全性的影响.基于本文计算结果,可得到如下结论:
1)与列车竖向荷载相比,竖向风产生的托起作用对桥梁影响更大,故在对龙卷风作用下桥梁动力响应研究中,不能仅考虑龙卷风的平面漩涡.当龙卷风移动路径ψ在60°~120°时,桥梁竖向动力响应幅值相对较大.
2)当车辆经过风荷载最大位置时,车辆的横向和竖向振动响应达到最大值,且车辆动力响应受龙卷风荷载和桥梁动力响应共同影响.EF1 级龙卷风作用下列车以150 km/h 通过桥梁时,尾车的横向位移和加速度最大,并且由头车至尾车,车体横向位移逐渐增大.
3)当龙卷风移动路径ψ在60°~90°时,列车的脱轨系数和轮轴横向力较大;当ψ为150°时,列车行车安全性指标最小,列车相对安全.对于龙卷风中心与列车组中间位置相遇的情况,列车中部和尾部车辆更容易发生行车安全问题.
4)轮重减载率相对于脱轨系数和轮轴横向力更容易超过规范限值,降低车速是保证龙卷风作用下列车行驶安全的有效措施.EF1级和EF1.3级龙卷风作用下,列车安全通过的车速阈值分别为180 km/h和114 km/h.

