北斗三号系统PPP-B2b信号定位服务模型及性能分析

田先才，张龙平，原 亮，徐君毅，孙伟杰

(1. 航天宏图信息技术股份有限公司，北京 100094；2. 北京卫星导航中心，北京 100094)

0 引言

北斗三号系统(BeiDou-3 Navigation Satellite Sys-tem，BDS-3)由空间段的卫星星座，地面段的主控站、监测站、上行注入站和用户终端等三部分组成，设计星座由30颗卫星组成，包括3颗地球同步轨道(Geosynchronous Orbit，GEO)卫星、3颗倾斜地球同步轨道(Inclined Geosynchronous Orbit，IGSO)卫星和24颗中圆地球轨道(Medium Earth Orbit，MEO)卫星。BDS-3融合了导航定位与通信数传的技术优势，与国外其他卫星导航系统相比，在提供基本定位导航授时(Positioning, Navigation, and Timing，PNT)服务功能的基础上，更加突出了高精度服务、短报文和位置服务，可以为全球用户提供定位导航授时、全球短报文通信和国际搜救三种服务，同时，还能为中国及周边地区用户提供星基增强、地基增强、精密单点定位(Precise Point Positioning，PPP)和区域短报文通信等四种区域服务。其中，PPP-B2b信号作为数据播发通道，通过BDS-3地球静止轨道(GEO)卫星播发BDS-3(24颗MEO卫星与3颗IGSO卫星)及其他全球卫星导航系统(Global Navigation Satellite System，GNSS)精密轨道和钟差等改正参数，为我国及周边地区用户提供PPP服务，覆盖区域如图1所示。

图1 PPP-B2b覆盖区Fig.1 Service area of PPP-B2b

近年来，PPP技术逐渐发展成为GNSS相关技术领域的热点研究方向之一，促使其在广域精密实时定位、低轨卫星定轨、水汽实时反演和电离层实时监测、精密授时等方面显现出广阔的应用前景。对于传统PPP技术，最初只能依靠国际GNSS服务(International GNSS Service，IGS)分析中心提供滞后一个星期的精密星历做事后处理，时效性受到了很大限制。近年来，由于用户对实时产品的迫切需求，国内外众多研究及商业机构陆续提供实时服务，2002年IGS成立了实时工作组，进行实时产品的相关研究；2007年，IGS开始运行IGS-RTPPP项目，实时估计卫星轨道和钟差；Furgo公司于2009年开始启动全球精密定位服务，采用分布在全球的监测站进行实时轨道、钟差的估计与解算，并通过GEO卫星向用户播发实时增强信息改正数；Trimble公司从2011年9月开始在全球范围内提供实时GNSS定位服务，其水平精度可以达到厘米级；2011年，状态空间域(State Space Represention，SSR)信息格式正式成为海事无线电技术委员会(Radio Technical Commission for Marine, RTCM)推荐的开放格式之一，多个国际分析中心采用SSR信息格式播发包含实时轨道、钟差改正的NTRIP数据流。

自BDS-3开通后，PPP-B2b信号开始逐步提供服务，用户最快可以实时获取高精度的轨道和钟差等误差改正信息。目前，关于PPP-B2b全套定位算法和技术要点的介绍还不太全面，本文从PPP-B2b的观测模型、随机模型、增强改正模型及参数估计模型等关键算法模型进行了推导和研究，并重点阐述了PPP-B2b定位与增强改正的方法。最后，采用多模GNSS跟踪网(Multi-GNSS Experiment，MGEX)和国际GNSS监测评估系统(international GNSS Monitoring & Assessment System，iGMAS)站观测数据，对BDS-3、全球定位系统(Global Positioning System，GPS)、BDS-3/GPS静态与动态PPP性能进行了验证与分析。

1 PPP-B2b定位数学模型

1.1 观测模型

常用的PPP模型有无电离层组合模型、UofC(半和)模型和非差非组合模型等。为了消除电离层的影响，本文结合无电离层组合模型，即通过对双频伪距和载波相位观测量的线性组合，消除一阶电离层延迟的影响，构建PPP-B2b观测模型

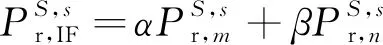
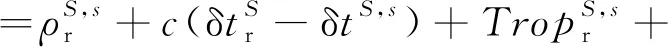
(1)

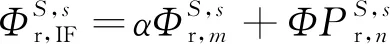
(2)

(3)

由于上述模型部分参数间存在很强的相关性，因此不能直接估计这些参数，通常是将相关的参数进行合并或者当作已知量以消除观测方程秩亏问题，可以进一步写成

(4)

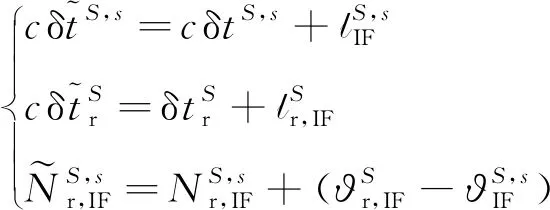
(5)

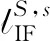
1.2 随机模型

PPP中通常采用的随机模型方法有卫星高度角法、信噪比法和方差分量估计法等。本文采用基于高度角法的随机模型，其表达式为

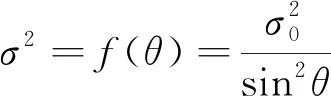
(6)

式中，为卫星高度角；为观测噪声的标准差；为观测量的方差。

当高度角大于一定阈值时，影响效果将显著减小，为了避免高度角高于阈值时对应观测量的权重占比不合理，在实际数据处理过程中常采用分段定权法，得到的伪距和载波相位观测量的方差为

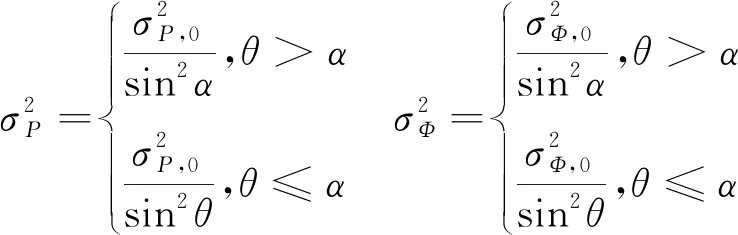
(7)

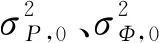
1.3 增强改正模型

BDS-3 PPP服务信息在PPP-B2b信号中播发，包括卫星掩码(Type1)、卫星轨道改正数及用户测距精度指数(Type2)、码间偏差改正数(Type3)、卫星钟差改正数(Type4)、用户测距精度指数(Type5)、钟差改正数与轨道改正数-组合1(Type6)、钟差改正数与轨道改正数-组合2(Type7)、预留(Type8-62)、空信息(Type63)。目前稳定正常播发的类型有Type1、Type2、Type3及Type4，其与广播星历与钟差之间的联系如图2所示。

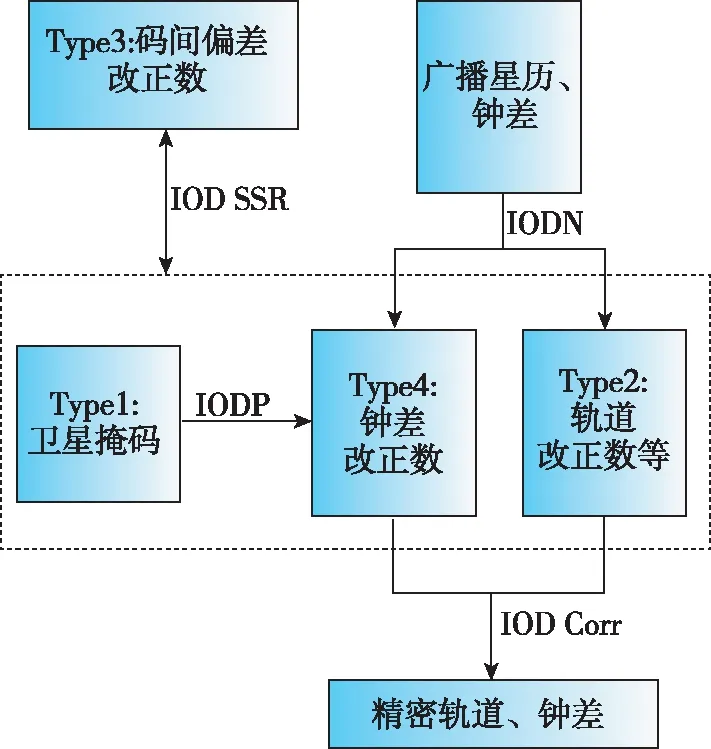
图2 PPP-B2b电文间的联系Fig.2 Links between messages of PPP-B2b

(1)卫星轨道改正

轨道改正信息包括的参数为轨道改正向量δ在径向、切向和法向的分量。轨道改正值用于计算卫星位置改正向量δ，同时还要联合利用广播星历计算出的卫星位置向量，改正的计算公式为

=-δ

(8)

式中，为经过轨道改正电文改正得到的卫星位置；为广播星历计算得到的卫星位置；δ为卫星位置改正数。

其中，卫星位置改正数δ的计算方法为

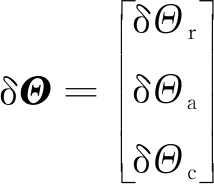
(9)

式中，、、分别为径向、切向和法向单位矢量；δ为PPP信息中获得的轨道改正矢量。

(2)卫星钟差改正

钟差改正电文包括的参数是相对于广播星历钟差的改正参数，具体改正方法为

(10)

式中，为经过钟差改正电文改正得到的卫星钟差；为广播星历计算得到的卫星钟差参数；为光速；δ为PPP-B2b电文中获得的钟差改正参数。

(3)伪距码间偏差改正

北斗各观测值都包含一个与信号跟踪模式相关的偏差，在同步处理各频率各类信号时，需要首先消除该偏差，实现各类信号同步处理。如果用户端使用的测距信号为B1Cp与B2ap信号，则PPP-B2b信号电文中播发的B1Cp、B2ap信号码间偏差分别为l、l，对于无电离层组合模型的码间偏差改正方法为

(11)

式中，、分别为B1Cp和B2ap载波中心频率(注：其他频点信号类似)。

在误差改正上，本文除了对轨道、钟差误差以及码间偏差进行了改正，对对流层延迟、地球自转效应等其他误差也进行了改正，具体改正与数据处理策略如表1所示。

表1 误差改正与数据处理策略

1.4 参数估计模型

在GNSS数据处理中，Kalman滤波是目前解算效率最高的滤波方法，由于该方法不用保存当前历元之前的所有数据，所以占用内存少，解算效率高，非常适用于PPP的解算工作，其状态方程与观测方程为

(12)

式中，、-1分别表示当前及前一历元时刻；为状态向量；,-1为状态转移矩阵；-1、-1分别为动态噪声向量及其协方差矩阵；、分别为观测噪声向量及其协方差矩阵；、分别为观测向量及设计系数矩阵。

在PPP-B2b中，状态向量包含了接收机位置与速度、接收机钟差、对流层湿延迟以及模糊度等参数，具体表示为

(13)

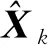
(14)

2 PPP-B2b实验分析

为了对BDS-3/GPS的PPP性能进行验证，实验选择了2021年5月1日—2021年5月15日MGEX和iGMAS站观测数据，站点均位于C59号卫星服务范围内(站点分布如图3所示)，定位模式分别采用单BDS-3、单GPS和BDS-3/GPS下的静态与动态(静态仿动态)模式。其中，动态模式定位时将测站坐标当成随机游走过程进行估计，其余参数的处理方法与静态定位相同。处理流程如图4所示。

PPP-B2b对北斗多个信号播发了改正信息，为了比较不同信号单系统及不同信号多系统融合的定位差异，分别对单BDS-3的B1CB2a、B1IB3I，GPS的L1L2，BDS-3的B1CB2a与GPS的L1L2融合，以及BDS-3的B1IB3I与GPS的L1L2融合等五种定位形式进行解算。下面以2021年5月10日MGEX中心的JFNG站为例，以4h为单位时间进行静态与动态模式下的定位解算，静态模式下各方向定位误差序列如图5～图7所示，动态模式下各方向定位误差序列如图8～图10所示。

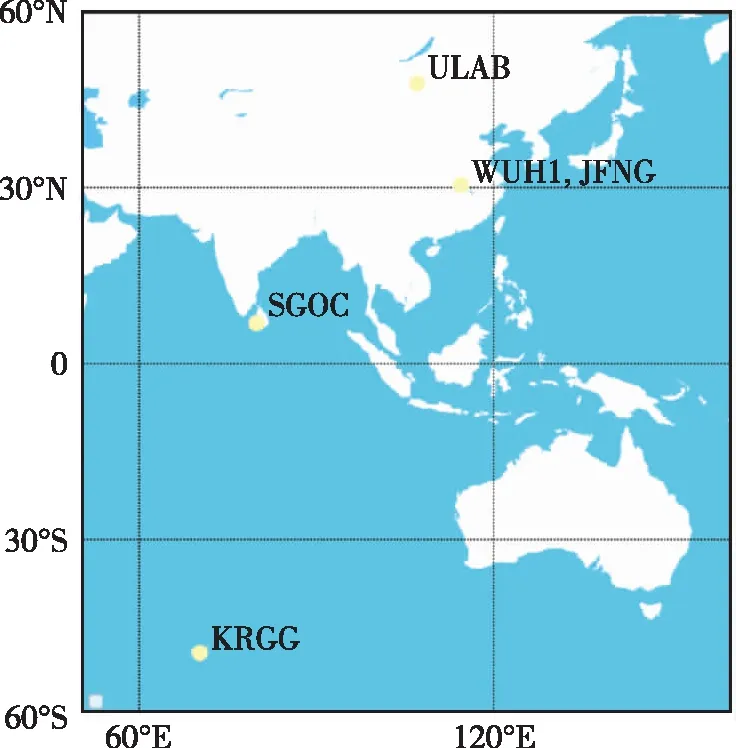
图3 站点分布图Fig.3 Layout of stations

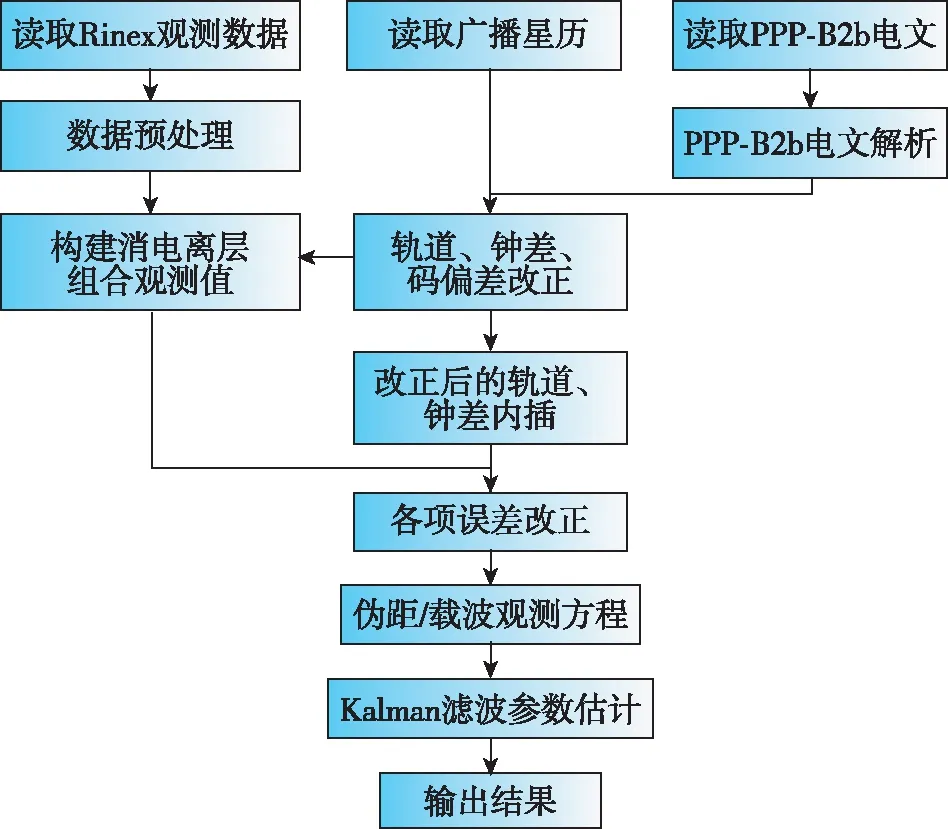
图4 PPP-B2b处理流程Fig.4 Process of PPP-B2b

从图5～图10可以看出，无论是静态还是动态定位模式，BDS-3与GPS融合的收敛性较任何单一系统都有很大的提升，并且收敛后误差分布比较平稳。为了验证收敛性与定位精度的整体性能，下面对JFNG站7天(5月1日—5月7日)的观测数据进行初步的收敛性实验分析，共得到42组(7天×6组)结果，并对不同收敛时刻下42组定位精度(RMS)求均值，如图11～图16所示。

图5 静态模式E方向定位误差Fig.5 East positioning error of static mode

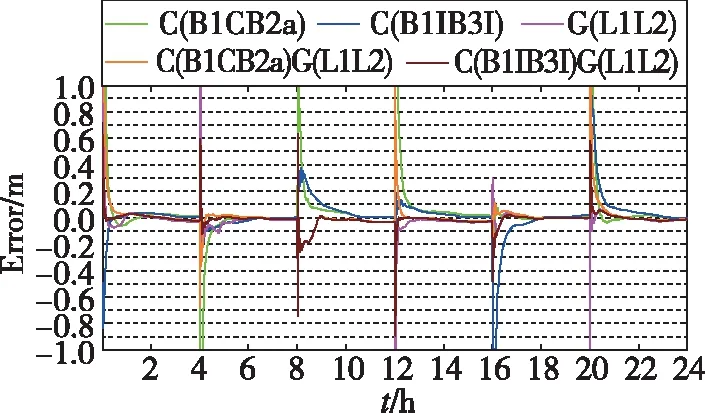
图6 静态模式N方向定位误差Fig.6 North positioning error of static mode

图7 静态模式U方向定位误差Fig.7 Up positioning error of static mode

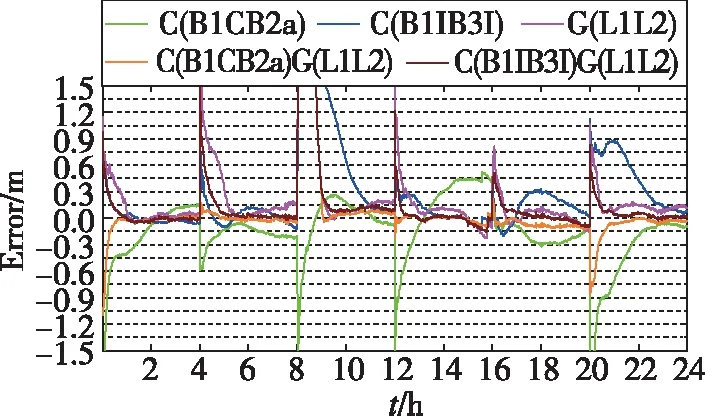
图8 动态模式E方向定位误差Fig.8 East positioning error of dynamic mode

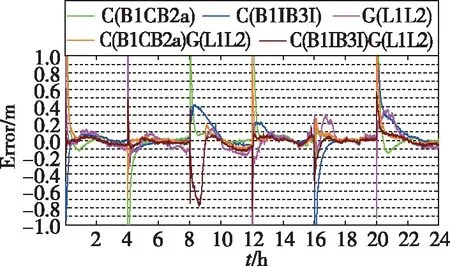
图9 动态模式N方向定位误差Fig.9 North positioning error of dynamic mode

图10 动态模式U方向定位误差Fig.10 Up positioning error of dynamic mode

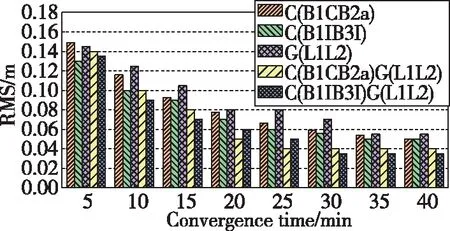
图11 静态模式E方向收敛时间与定位精度Fig.11 East convergence time and positioning accuracy of static mode

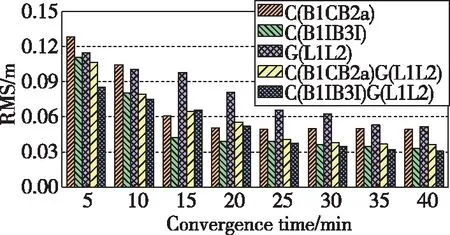
图12 静态模式N方向收敛时间与定位精度Fig.12 North convergence time and positioning accuracy of static mode

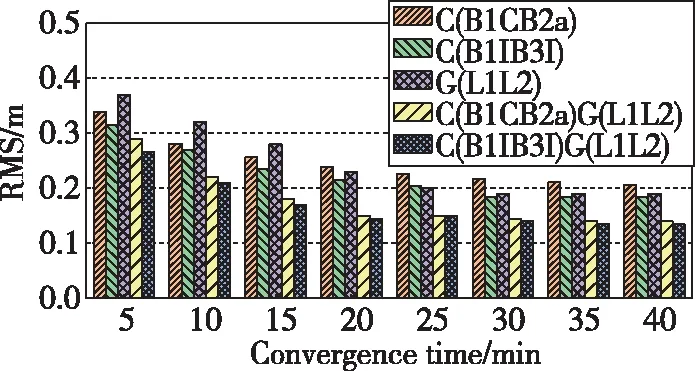
图13 静态模式U方向收敛时间与定位精度Fig.13 Up convergence time and positioning accuracy of static mode

图14 动态模式E方向收敛时间与定位精度Fig.14 East convergence time and positioning accuracy of dynamic mode

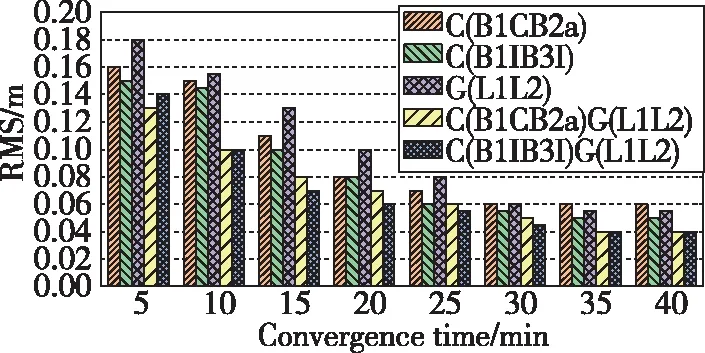
图15 动态模式N方向收敛时间与定位精度Fig.15 North convergence time and positioning accuracy of dynamic mode

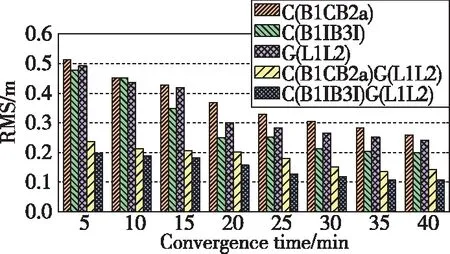
图16 动态模式U方向收敛时间与定位精度Fig.16 Up convergence time and positioning accuracy of dynamic mode

从图11～图16收敛时间与定位精度态势可以看出，随着收敛时间的延长，各方向定位精度越来越高，直到完全收敛至一定精度。静态模式下，单、双系统在30min内可以达到E方向0.05m左右、N方向0.04m左右、U方向0.15m左右的精度；动态模式下，单、双系统在30min内可以达到E方向0.09m左右、N方向0.06m左右、U方向0.20m左右的精度。

为了充分验证和分析PPP-B2b在服务覆盖区内的定位精度，选取了iGMAS的WUH1以及MGEX的JFNG、ULAB、SGOC、KRGG等5个站15天的观测数据进行实验分析，并统计不同模式下的定位精度(单系统30min收敛时间、双系统20min收敛时间后的定位精度)，最后对每个站在不同定位模式及组合下共90组(15天×6组)的定位精度(RMS)求均值，如表2所示。

从表2各个站统计结果可以看出，对于单GPS，静态水平、高程定位精度均值分别为0.104m、0.199m，动态水平、高程定位精度均值分别为0.152m、0.346m；对于BDS-3平稳过渡信号，单系统静态水平、高程定位精度均值分别为0.103m、0.194m，单系统动态水平、高程定位精度均值分别为0.159m、0.305m；BDS-3/GPS双系统静态水平、高程定位精度均值分别为0.080m、0.144m，双系统动态水平、高程定位精度均值分别为0.105m、0.255m；对于BDS-3全球新体制信号，单系统静态水平、高程定位精度均值分别为0.107m、0.202m，单系统动态水平、高程定位精度均值分别为0.169m、0.382m；BDS-3/GPS双系统静态水平、高程定位精度均值分别为0.082m、0.150m，双系统动态水平、高程定位精度均值分别为0.112m、0.274m。

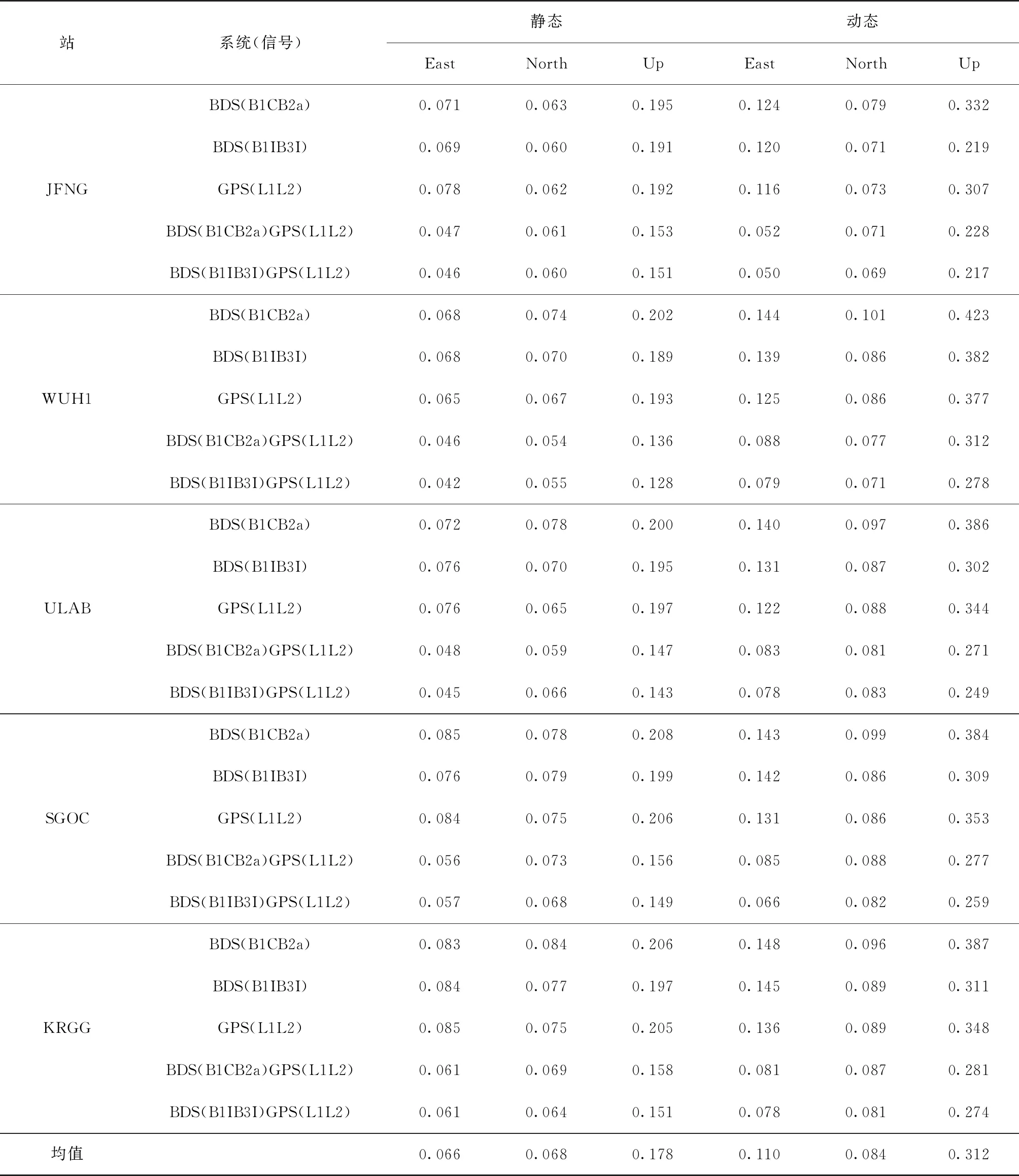
表2 PPP-B2b定位精度(RMS，单位：m)

3 结论

首先，构建了PPP-B2b数学模型，并详细阐述了PPP-B2b技术要点。然后，根据BDS-3 C59号卫星播发的轨道、钟差等改正信息，进行了定位精度与收敛性的验证分析。最终分析结果可以归纳为以下几点：

1)无论是静态还是动态定位模式，BDS-3/GPS融合的收敛性较任何单一系统都有很大的提升，并且收敛后误差分布比较平稳；

2)对于单系统，BDS-3平稳过渡信号与全球新体制信号及GPS的L1L2信号定位精度基本一致，对于双系统，BDS-3平稳过渡信号/GPS融合与BDS-3全球新体制信号/GPS融合定位精度基本一致；

3)在30min收敛时间内，单系统静态水平、高程定位精度均值分别为0.105m、0.198m，动态水平、高程定位精度均值分别为0.160m、0.344m，在20min收敛时间内，双系统静态水平、高程定位精度均值分别为0.105m、0.198m，动态水平、高程定位精度均值分别为0.160m、0.344m，收敛性和定位精度均满足BDS-3PPP服务指标要求。

致谢

感谢iGMAS、MGEX提供的数据。