MEMS陀螺仪的高精度标定方法
陈海明,李荣冰,王双甲,刘建业
(1.南京航空航天大学导航研究中心,南京 211106;2.西安飞行自动控制研究所,西安 710065)
0 引言
微机电(Micro-Electro-Mechanical System,MEMS)陀螺仪作为MEMS传感器典型代表之一,具有体积小、成本低、功耗低和可靠性高等优点,是惯性导航领域的研究热点。MEMS陀螺仪由于机械结构或制造过程中引入的机械误差,几乎都存在因加速度产生的测量误差,该误差被称为加速度敏感漂移误差。过去针对MEMS陀螺仪的建模研究中,因为研究对象的测量精度较低,大多只考虑了零偏误差、非正交误差和标度因数误差对陀螺仪测量精度的影响,没有考虑加速度敏感漂移误差。近年来,随着MEMS陀螺仪在电子学控制、微结构、工艺平台以及集成应用技术等方面取得突破,其测量精度得到了明显提高,而建立考虑加速度敏感漂移误差的MEMS陀螺仪输出模型是提高其测量精度,使其在更高精度导航领域应用的重要前提。
一般情况下,陀螺仪和加速度计组成惯性测量单元,用于测量角速率和加速度。其中,角速率测量单元由陀螺仪构成,其输出角速率包含非正交误差和与输入加速度相关的加速度敏感漂移误差。为了提高陀螺仪的测量精度,本文设计了一种同时标定MEMS陀螺仪非正交误差和加速度敏感漂移误差的标定方法,该方法适用于零偏稳定性优于1(°)/h的MEMS陀螺仪,并通过试验进行了验证。标定过程中,加速度数据由惯性测量单元中的加速度计提供,且加速度计轴向与陀螺仪轴向重合,因此,加速度计输出数据在经过误差修正后就是陀螺仪对应轴向的加速度值。
1 包含加速度敏感漂移误差和非正交误差的MEMS陀螺仪误差建模


(1)
其中,为标度因子;为零偏误差。
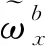

(2)
根据加速度敏感漂移误差定义,陀螺仪的加速度敏感漂移误差与陀螺仪所受比力之间的关系可以表示为
=++
(3)
其中,、和分别是陀螺仪在3个轴向上受到的比力;、和分别是各轴向比力对陀螺仪的加速度敏感漂移系数。
结合式(2)与式(3),可以得到考虑非正交误差与加速度敏感漂移误差的轴陀螺仪输出模型

+++
(4)
同理可得轴和轴陀螺仪输出模型

+++
(5)

+++
(6)
矩阵表达式可以表示为


(7)
可简化为

(8)
其中,为零偏不稳定性造成的误差,该误差项可以通过对角速率原始数据进行分组平滑处理后得到消除。
从式(8)可以看出,为了提高陀螺仪的输出精度,需要标定和补偿陀螺仪的零偏、非正交误差,以及标度因子误差矩阵和加速度敏感漂移误差矩阵。
2 基于误差模型解耦的非正交与加速度敏感漂移系数转台标定方法
传统的陀螺仪多位置转台标定只考虑了陀螺仪的零偏和非正交误差对陀螺仪输出的影响。为了对加速度敏感漂移误差进行标定与修正,本文设计了16位置转台标定方案,标定步骤如下:
1)转动双轴转台内外框,使转台位置依次如图1所示,分别采集静态下16个转台位置的三轴MEMS陀螺仪和加速度计的数据;
2)对采集到的陀螺仪和加速度计的数据进行分组平滑处理;
3)对MEMS陀螺仪的零偏误差进行标定与补偿;
4)同时对陀螺仪的加速度敏感漂移误差和非正交误差进行标定。
零偏稳定性优于1(°)/h的陀螺仪在减小噪声的影响后可以准确地敏感到地球自转角速率,所以本方案将选择地球自转角速率在3个轴上的分量作为陀螺仪的激励角速率。

图1 转台标定位置示意图Fig.1 Position diagram of turntable
在进行转台位置调整时,不需要采集陀螺仪数据,所以转台的转动方式不会对标定结果产生影响,只需要调整双轴转台的内外框,使转台位置依次如图1中所示的16个位置状态即可。
因为需要对陀螺仪的加速度敏感漂移系数进行标定,所以需要确保每个轴向上的陀螺仪除了受到2个以上的角速率激励外,还要受到至少2个不同数值的比力激励。本文方法选择-,0,作为对陀螺仪的激励加速度,在同时考虑激励的充分性与标定效率的情况下,设计了图1所示的16个转台位置状态。
3 零偏误差校准
对于陀螺仪零偏的标定与补偿,此处仅以轴方向上的陀螺仪作为样例进行分析。







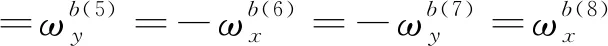

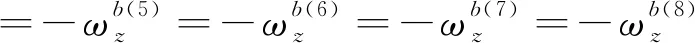
(9)





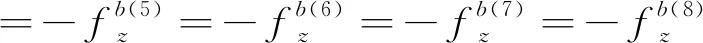
(10)
将上述式(9)和式(10)分别代入式(8)中,可以得到在前8个位置状态下轴陀螺仪的输出角速率与3个轴上实际的输入角速率和比力的关系为
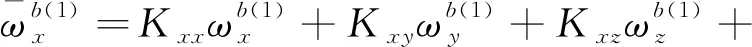

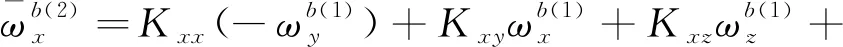


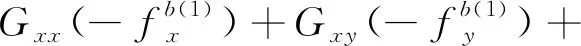


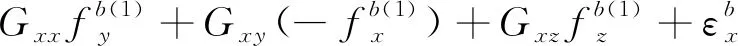
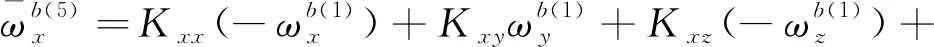
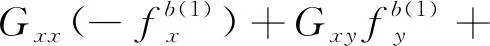





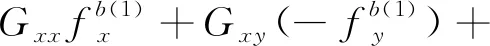

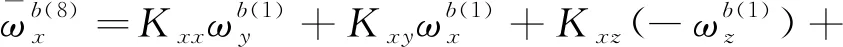
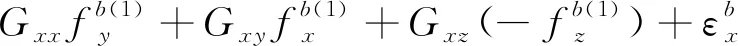
(11)
将式(11)中的8个等式左、右两边各自两两相加,不难发现,由于在状态转动时,位置状态的选择保证了外界输入的角速率与加速度对陀螺仪输出的影响两两抵消,所以轴陀螺仪的零偏误差可以表示为

(12)
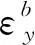
补偿零偏误差后,陀螺仪在16个位置状态下的角速率输出与外界施加在3个轴上的角速率与加速度的关系可以表示为

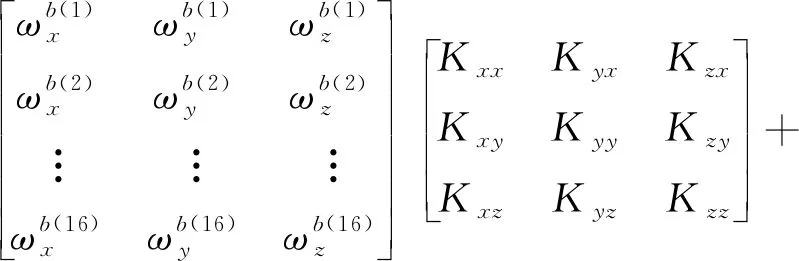

(13)
式(13)可以简化为
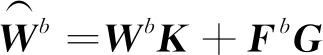
(14)
4 非正交误差和加速度敏感漂移误差校准
从式(14)可以看出,在补偿陀螺仪零偏误差后,陀螺仪的输出角速率中,非正交误差与加速度敏感漂移误差仍然相互耦合,且很难通过物理手段将2个耦合项进行解耦。若仅仅使用数学方法,可以将式(14)等式右侧的与合并为一项,得到

(15)
此时,可以利用最小二乘法对方程式(15)直接进行拟合求解,但因为矩阵中数值接近于0的元素较多,所以矩阵接近于奇异矩阵,最终导致矩阵方程求解的误差较大。因此,需要改进对非正交误差和加速度敏感漂移误差的标定方法。
本文利用两组测量数据,分别计算加速度敏感漂移误差矩阵与非正交误差矩阵并相互迭代,对这2个误差矩阵进行求解。下面给出迭代方法。


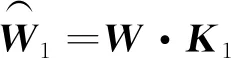
(16)
因为不是奇异矩阵,此时利用最小二乘法的求解法则,对超定方程式(16)中的进行如式(17)所示的拟合求解,即可得到所需标定的非正交误差矩阵
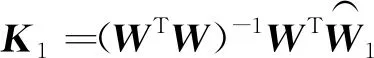
(17)
根据第一组数据计算出非正交误差矩阵,并将该结果代入第二组数据,得到

(18)
同理,可以通过最小二乘法解算超定方程式(18),求得加速度敏感漂移误差矩阵,然后将结果代入第一组数据,对非正交误差进行更新。每次迭代,以经过校正后的陀螺仪对地球自转角速率的敏感误差作为对迭代结果准确性的评估依据。如此循环往复,在多次迭代后,可以得到较为精准的非正交误差矩阵和加速度敏感漂移误差矩阵。
在完成对非正交误差、加速度敏感漂移误差和陀螺仪零偏的标定后,根据式(19)可以得到经过修正后的更高精度的陀螺仪输出
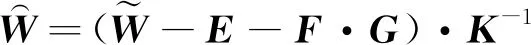
(19)
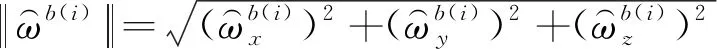
(20)
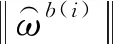

(21)

(22)

5 非正交误差和加速度敏感漂移误差校准方法验证与分析
本文选用了高精度双轴温控转台进行16个位置的转台标定,并采用3个国产高精度MEMS陀螺仪和3个MEMS加速度计构建了姿态测量单元,对上文阐述的标定方法进行验证。选用的3个陀螺仪实测输出零偏不稳定性分别达到了0.731(°)/h、0.367(°)/h、0.916(°)/h,Allan方差曲线达到最低点时的采样时间分别为655s、681s、622s。
进行陀螺仪转台标定时,转动转台内外框,使转台位置依次满足图1中16个位置状态,每个位置处数据采集时长为20min。在完成了一个位置状态下的数据采集后,根据Allan方差分析曲线最低点处的采样时间对原始数据进行分组平滑,以减小零偏不稳定性的影响。
在陀螺仪Allan方差分析曲线达到最低点时,采样宽度与采样间隔和采样数据量之间存在以下关系
=·
(23)
以为分组长度,分别将3个轴的陀螺仪原始输出数据分割成(=,,)组,与每个轴陀螺仪输出数据总量的关系为
=-+1
(24)
其中,第组数据是陀螺仪输出的总体数据中第个数据到第+-1的数据。


(25)
根据分组平滑后的陀螺仪在位置状态(1)处~(8)处的数据,按式(11)求取3个轴向上的陀螺仪的零偏,分别为-1.709(°)/h、30.633(°)/h和-3.380(°)/h。
采用上文阐述的迭代解算方法对角速率测量系统的非正交误差和加速度敏感漂移误差进行求解。在迭代过程中,初始迭代误差为2.64(°)/h,在迭代超过800次后,每次迭代时误差的降低约为1×10(°)/h,此时迭代已趋于稳定,约1.29(°)/h。标定结果分别如表1和表2所示。
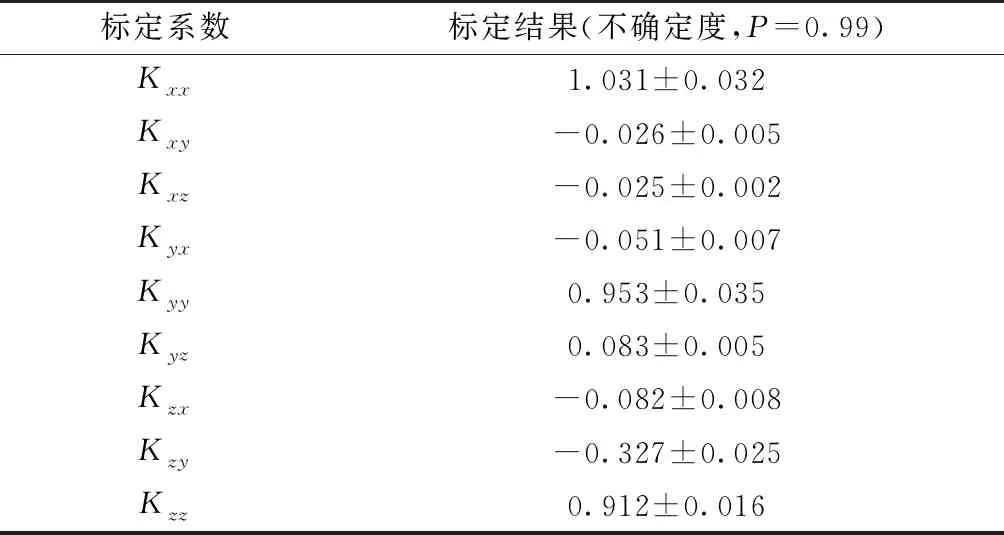
表1 陀螺仪非正交误差系数标定结果
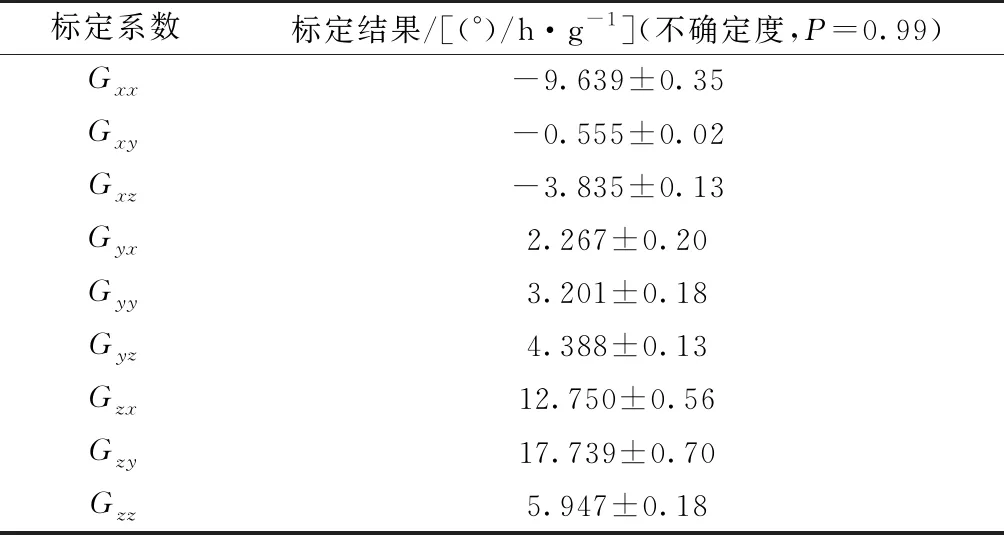
表2 陀螺仪加速度敏感漂移误差系数标定结果
从表2可以看出,某轴向加速度对该轴向陀螺仪的影响并不一定是最大的,加速度敏感漂移误差对陀螺仪输出的影响是综合性的。
本文选用的加速度计的零偏稳定性为100μ,由加速度测量误差引起的陀螺仪加速度敏感漂移误差的最大值约为0.18(°)/h。
本文陀螺仪标定方法的标定结果与常规标定方法所得结果的对比如表3所示。
由表3可以看出,本文提出的16位置标定方法与传统的6位置和19位置的陀螺仪标定方法精度相当。但相较于传统的6位置标定方法,16位置标定方法不需要频繁地改变对陀螺仪的角速率激励;同时,本文方法对不同转台位置间的转动方式没有严格的要求,且位置状态相对较少,所以与19位置标定方法相比操作更方便。


表3 16位置标定与常规的6位置标定、19位置标定结果对比

从表4和图2可以看出,在对非正交误差和加速度敏感漂移误差进行标定和修正后,陀螺仪敏感地球自转角速率误差值Δ的均值与标准差均小于补偿前,这证明了上文提出的对非正交误差和加速度敏感漂移误差标定可以提高MEMS陀螺仪的测量精度和性能。在经过误差标定和修正后,陀螺仪对地球自转角速率的测量误差和测量标准差分别降低了55.7%和25.9%,这证明了该算法的有效性,为MEMS陀螺仪高精度建模工作提供了参考。

表4 Δωpre与Δωaft的均值与标准差
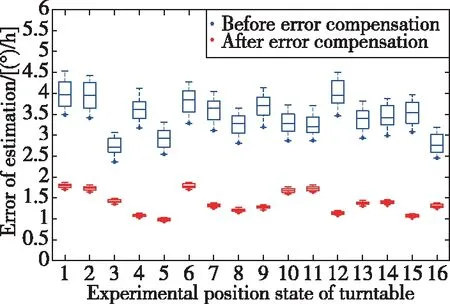
图2 非正交误差与加速度敏感漂移误差补偿前后Δωie对比曲线Fig.2 Δωie before and after compensating non-orthogonal error and acceleration-sensitive drift error
6 结论
本文设计了针对MEMS陀螺仪的16位置转台标定方案,基于惯性测量单元中MEMS陀螺仪非正交误差和加速度敏感漂移误差相互耦合的特性,提出了一种利用两组角速率数据迭代求解非正交误差系数和加速度敏感漂移误差系数的方法。同时,本文以陀螺仪对地球自转角速率的测量误差作为陀螺仪输出模型精度性能的评估依据,并展开试验验证。结果表明,通过对非正交误差和加速度敏感漂移误差的标定与修正,微惯性测量单元中陀螺仪的测量精度和性能得到了明显的提高,为MEMS陀螺仪高精度建模工作提供了参考,为其在高精度导航领域的应用奠定了基础。

