具有动态领导者的多智能体系统分组一致性控制
胡顺伟,陈向勇, 邱建龙,赵 峰
(临沂大学自动化与电气工程学院,山东临沂 276005)
0 引言
一致性控制是多智能体系统协同控制的关键问题。一致性控制旨在利用智能体自身和相邻智能体的状态信息设计控制器,实现群体状态的趋同。当前,一致性思想已在微电网均衡调压、无人机协同,以及编队控制中得到了广泛的应用,因此备受关注,相关的成果也接连涌现。
文献[6-7]研究了一类线性多智能体系统,通过设计动态事件触发协议,在不需要全局信息的情况下实现了无领导者的一致性控制。文献[8]则通过状态分解的方法,实现了可以隐藏初始状态信息的平均一致性控制。文献[9]通过在触发间隔引入估计器,减少了相邻触发间隔的状态偏移,实现了有领导者的跟踪一致性控制。相较于无领导者一致性和初值平均一致性,有领导者的跟随一致性问题复杂度更高,更具有挑战性。文献[10]研究了在切换拓扑下有领导者的线性多智能体系统,利用系统在触发时刻的状态设计了控制器,实现了不依赖于全局信息的领导-跟随一致性控制。文献[11]设计了一个虚拟领导者,利用非周期间歇通信机制,解决了带时滞非线性多智能体系统的领导-跟随问题。文献[12]分别设计了集中式和分布式的控制器,在两种情况下分别实现了领导-跟随渐近一致性控制。在上述文献研究中,领导者的动力学模型不存在控制输入且模型相对保守。目前,对领导者存在控制输入的动力学模型的研究还相对较少,具有一定的研究意义和研究前景。
此外,随着工业生产要求的提高,智能体往往要求完成多目标任务,智能体之间的信息交互不再是简单的合作关系,而是伴随着合作-竞争的信息交互。在合作-竞争信息交互下,具有合作信息交互的智能体的状态趋于相同值,具有竞争信息交互的智能体的状态趋于相反值。这种情况下,传统的群体一致性控制器变得不再适用,需要一些新的分组协议来实现这种控制目标。文献[13]通过引入预设时间函数,在事件触发机制下实现了一阶多智能体系统的分组一致性控制。文献[14]讨论了合作、强竞争、弱竞争三种交互关系,设计了一种切换控制律,实现了异构二阶多智能体系统分组一致。文献[15]设计了一个非光滑控制器,利用自适应控制消除了对全局信息的依赖,解决了线性多智能体系统的领导-跟随一致性问题。然而,这些研究所提出的方法只适用于具有一阶、二阶或线性动力学模型的多智能体系统,而实际中多智能体系统模型大多是非线性的。
需要指出的是,一些领导-跟随一致性控制问题中所研究的领导者模型是不具有控制输入的,此类模型保守性较大,适用范围较小。理论上,这种模型可以看作领导者的控制输入为零时的一类特殊情况。其次,相关文献往往仅考虑了单一合作或竞争的信息交互,对于合作-竞争交互给系统带来的影响并没有进一步的研究和说明。事实上,合作-竞争交互共存时给系统带来的影响是显著的,它不仅体现在实现一致性行为轨迹上的不同,而且在网络拓扑结构上也发生了明显的变化,一些群体一致性拓扑结构性质也变得不再适用。此外,非线性问题一直是系统控制的难点和重点,在考虑动态领导者和合作-竞争机制后,实现非线性多智能体系统一致性更具困难和挑战。
基于上述分析,本文主要研究了在合作-竞争交互下具有动态领导者的非线性多智能体系统的分组一致性控制问题。主要贡献如下:
1)相较于文献[10]和文献[12]中不具有控制输入的领导者动力学模型,本文考虑了具有非零控制输入的领导者,并且领导者的输入对每个跟随者都是未知的。传统的零输入领导者可看作是本文的一种特殊情况。
2)本文考虑了合作-竞争交互机制,相较于文献[16-18]中单一合作或竞争交互,本文研究的问题复杂度更高。
3)利用分组机制设计的控制器,适用范围更加广泛,本文设计的控制器不仅适用于合作-竞争交互的智能体系统,对于单一合作或竞争交互的多智能体系统也适用。
1 预备知识
1.1 图论

1.2 问题描述
考虑如下由1个领导者和个跟随者组成的非线性多智能体系统

(1)
其中,∈和∈分别代表领导者智能体的状态和控制输入。∈,∈分别代表跟随者智能体的状态和控制输入。:×→是在时间上连续可微的已知的非线性函数。、是具有适当维数的常数矩阵。
在文献[8]和文献[9]中,领导者不带有控制输入,这可以看作是系统(1)在()=0时的一种特殊情况。而本文中研究的领导者具有控制输入且与跟随者的相对状态无关,其相对于跟随者是未知的。
与系统(1)相关的符号图是结构平衡的,并且包含一个由领导者作为根节点的有向生成树。如果领导者是智能体的邻居,则0=1,否则0=0。
若符号图是结构平衡的,则存在一个符号矩阵=diag(,,…,),使得矩阵所有项都是非负的。其中,当节点处于同组时=1,当节点处于不同组时=-1。
(,)是可稳的。

非线性函数满足下列不等式
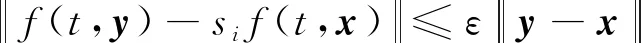
(2)
其中,>0是一个常数。
假设1是实现分组一致性控制的一般假设条件,在此条件下满足图拉普拉斯矩阵的一些特殊性质。假设2是保证Riccati不等式可解的条件。假设3中()是一致有界的,这在实际控制中是可行的。假设4是一类Lipschitz-like条件,用于解决分组一致性控制中非线性函数带来的困难。
当如下条件(3)被满足时,系统(1)可实现领导-跟随分组一致性控制。

(3)
跟随者智能体和领导者之间的状态误差定义为
()=()-()
(4)
由引理1和上述等式可知,本文主要解决的问题是在合作-竞争交互的多智能体系统(1)中设计分组控制器和,使得
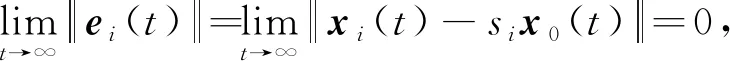
(5)
成立,从而实现系统(1)的领导-跟随分组一致性控制。
2 主要结果
首先,对误差系统(4)求导可得

=()+()+(,)-
(()+()+(,))
(6)
为了在符号图中实现系统(1)的分组跟随一致性控制,设计如下的控制器
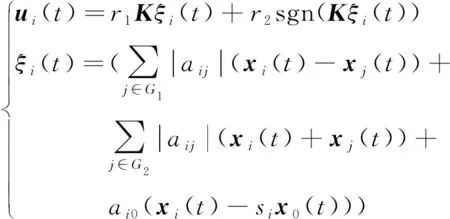
(7)
其中,,>0,是在下文中被设计的参数;∈表示智能体与智能体属于同一组,∈表示智能体与智能体属于不同组;表示领导者与跟随者是否同组,同组=1,不同组=-1。
合作-竞争交互在控制器(6)中体现为同组智能体之间为合作关系,其状态最终趋于相同值;不同组智能体之间为竞争关系,其状态最终趋于相反值。本文考虑的是二分组情况,智能体的邻居智能体只属于或,且∈∪,这种分组机制相较于文献[17]和文献[20]中群体一致性更具有应用前景。
结合上述所设计的控制器(7),式(6)可改写为如下紧凑形式

(⊗)sgn((⊗)())-
(⊗)()+()
(8)
其中,=+,=diag(,,…,0)表示领导者与跟随者的通信关系,表示由个跟随者智能体组成的通信拓扑图的拉普拉斯矩阵,
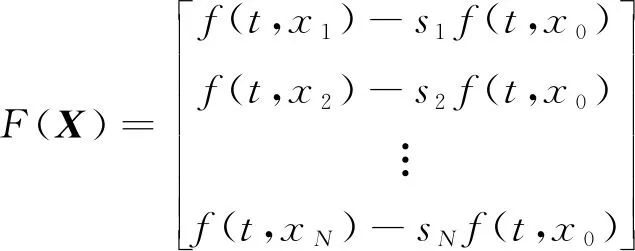
(9)
之后,对误差进行如下变换

(10)


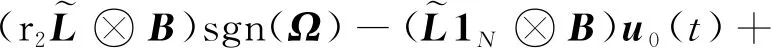
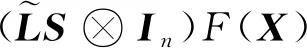
(11)

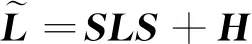
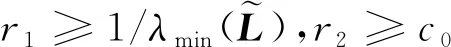
+-2++<0
(12)
选择Lyapunov函数为
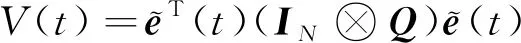
(13)
对式(13)求导可得

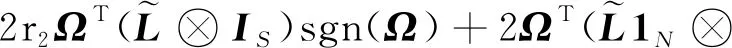
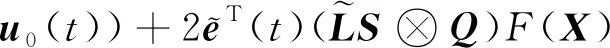



)()
(14)
结合假设4,式(15)成立

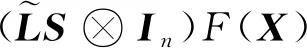
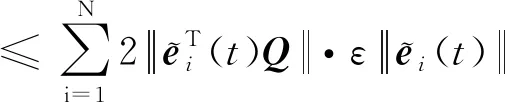
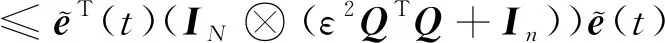
(15)


(⊗)sgn()+(⊗)sgn()

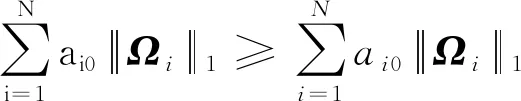
(16)
根据假设3可知
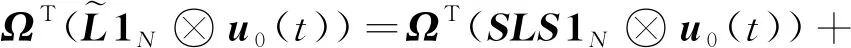

(17)
成立,因此,式(14)可写为
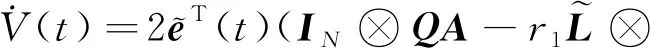



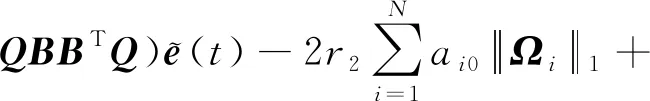
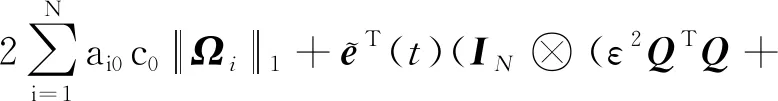


(18)
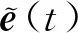
控制器(7)可以进一步转化为(19),控制器(19)可以有效地消除抖振现象。
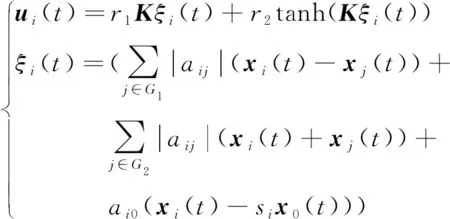
(19)
3 数值仿真
考虑由1个领导者和5个跟随者构成的多智能体系统,如图1所示,其中,领导者0和智能体1,2,3为同组;智能体4和5为同组。

图1 通信拓扑图Fig.1 Communication topology
由图1可以计算出
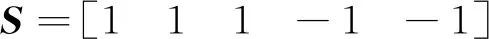
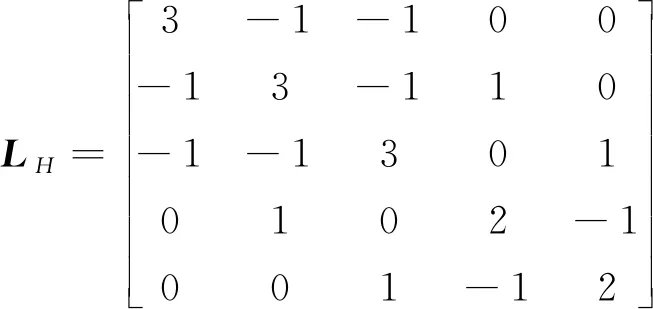

选择系统的参数如下


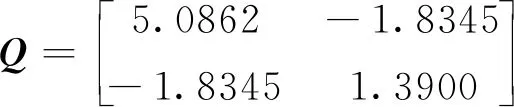
可得

设定系统初始状态值为
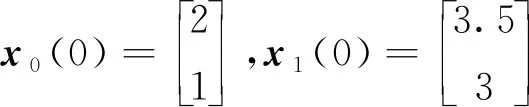
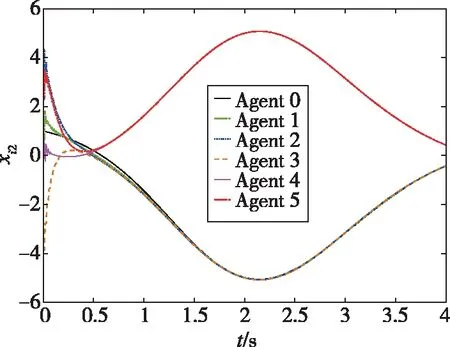
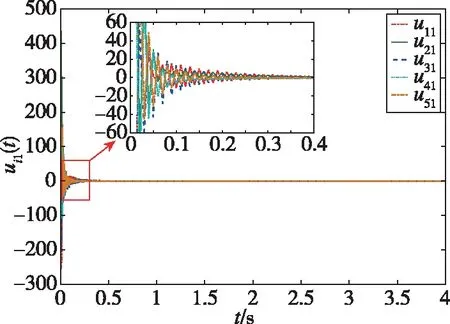
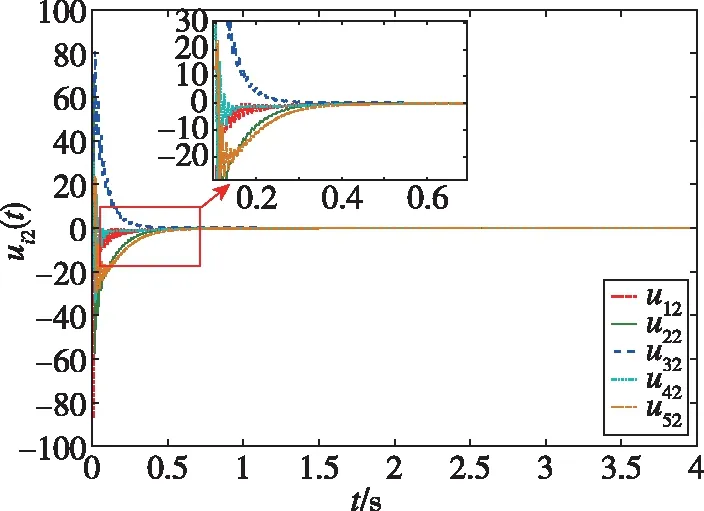
仿真结果如下:图2所示为智能体0~5随时间发生变化的状态轨迹图,图3所示为跟随者1~5与领导者0的状态误差轨迹图,图4所示为每个跟随者的控制输入轨迹图。从图2可以看出,跟随者1、2、3和领导者0的状态最终趋于一致,而跟随者4、5和领导者0的状态最终趋于相反值。从图3可以看出,同组的状态差收敛于0,不同组的状态和收敛于0。从图4可以看出,由于设计了较大的反馈增益参数,控制输入量在前0.5s内较大,收敛较快。通过仿真分析可知,在所设计的控制器(19)下,实现了动态领导者下的系统(1)的分组-跟随一致性控制。图5所示为系统(1)在反馈控制器()=ξ()时的状态误差轨迹,与图3的结果进行比较,可以发现,在相同时段内本文所设计的控制器可以实现更好的收敛性能。

(a)
(b)

(a)

(b)
(a)
(b)
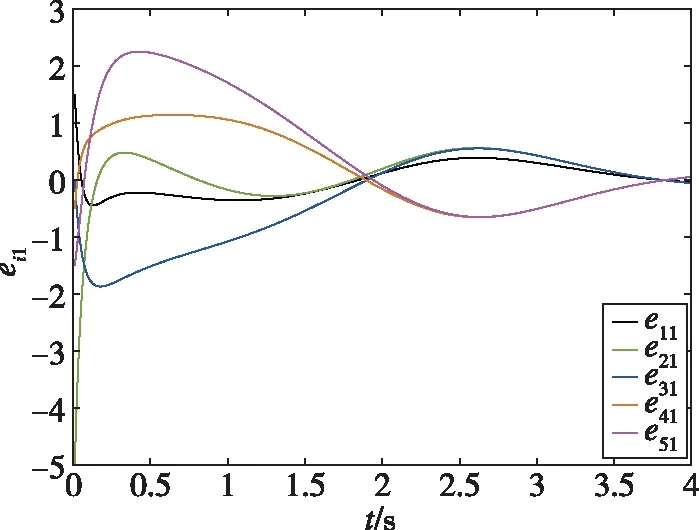
(a)
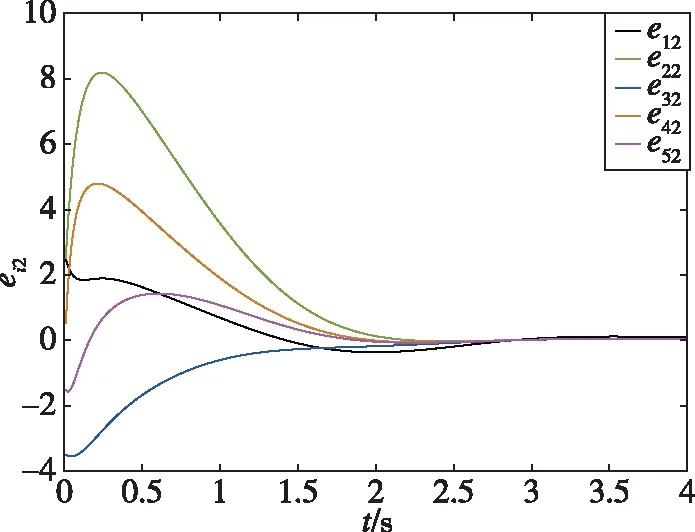
(b)
在一定的取值范围内,,选取的越大,则系统初始时刻的控制输入量越大,系统的收敛速度越快,控制量曲线越抖。因此,这里需要视情况折中处理,而在理论上选择的是满足条件的边界值。 事实上,存在不满足假设条件的参数也可以使系统稳定,因为定理1给出的是一个充分条件而非必要条件。
4 结论
本文研究了一类非线性多智能体系统的领导-跟随一致性控制问题。1)考虑领导者智能体具有非零控制输入的情况,基于邻居智能体的相对状态信息,设计了分布式控制器。2)仿真结果表明,本文设计的控制方案可以使得具有动态领导者的非线性多智能体系统在合作-竞争交互网络中实现分组-跟随一致性控制。3)未来的研究工作将考虑时滞影响,在有限时间内实现分组一致性控制。此外,本文设计的控制器是基于连续状态的,如何设计一个利用离散状态的脉冲控制器或事件触发控制器也是下一步的研究方向。

