GNSS多径抑制基带处理算法综述
邵 晨,曾庆化,2,3,邱文旗,许 睿
(1. 南京航空航天大学导航研究中心,南京 211106;2.先进飞行器导航、控制与健康管理工业和信息化部重点实验室,南京 211106;3.卫星通信与导航江苏高校协同创新中心, 南京 211106)
0 引言
全球导航卫星系统(Global Navigation Satellite System,GNSS)多径效应是指GNSS信号由于传输过程中存在遮挡,使接收信号中混有多径信号,造成信号幅值、载波相位和伪码延迟变化,引入定位解算误差,从而影响接收机定位精度的现象。根据伪随机噪声码(Pseudo Random Noise code,PRN)的自相关特性,当多径信号相对于直达信号的延迟在1个码片之内时,接收机接收的合成信号和本地产生信号之间的相关函数发生畸变,产生解算误差,这种由多径效应引起的误差称为多径误差。
随着GNSS现代化进程的推进,用户对于定位精度的要求也越来越高。影响GNSS定位精度的误差有很多,部分如钟差、对流层误差、电离层误差等可以通过改善模型、差分技术等方法进行抑制;而多径误差由于没有空间相关性,很难通过上述方法削弱,在误差源中的影响越来越大。因此,研究多径抑制技术对提高卫星导航定位精度具有重要意义。
由图1可知,多径误差产生的环境分为视距(Line-of-Sight,LOS)环境和非视距(Non-Line-of-Sight,NLOS)环境,视距环境下接收信号中含有直射信号,而非视距环境下的接收信号中没有直射信号。由于GNSS多径抑制基带处理算法仅适用于视距环境下多径误差的抑制,本文对非视距环境下的多径误差抑制技术不再详述。

(a) 非视距环境
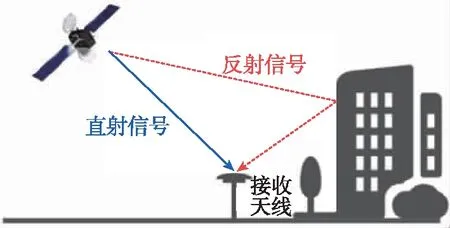
(b) 视距环境图1 多径误差生成过程Fig.1 Generation of multipath errors
视距环境下,多径误差抑制技术分为天线增强技术、基带处理算法和后处理技术三类,如图2所示。

图2 多径抑制技术Fig.2 Multipath mitigation technique
天线增强技术通过改进天线,使方向图主瓣对准直射信号方向,减少反射多径信号的接收,该方法主要在硬件层面通过天线选址、特殊天线、安装扼流圈等方式,抑制来自地面或低仰角的多径信号,但难以消除来自空中的多径信号。
基带处理算法主要通过分析信号结构,改进跟踪环,减小或消除多径信号对于自相关函数的影响,从而减小多径误差。
后处理技术通过对接收机测量数据进行后期处理以减小多径误差。如利用高斯牛顿方法跟踪多径增益及延迟参数,利用后期建筑信息协助多径判断进行选星,该类方法需要其他辅助信息和大量高精度测量数据,多径误差抑制效果好但实时性较差。
上述多径抑制技术中,基带处理算法受信号体制影响较大,卫星播发信号的不断改善和发展给多径抑制基带处理算法的研究带来了更大的机遇和挑战。本文从信号体制角度出发,对GNSS多径抑制基带处理算法的研究现状,典型算法的基本原理、优缺点和发展趋势做了较为详细的论述,其中部分典型算法如表1所示。
由表1可知,多径抑制基带算法目前的相关研究分为两类:第一类是对传统多径抑制算法进行研究,提高传统算法的跟踪精度和抗干扰性能,典型算法有窄相关技术、ELS、CCRW和MEDLL等;第二类是对新体制信号如北斗B1C、B2a信号等进行研究,充分利用多峰、数据导频分离、主瓣带宽大等信号结构特点来提高环路跟踪性能,如基于去模糊的多径抑制算法,能有效抑制或消除BOC信号的多峰特性从而避免误锁,同时获得更好的抗多径性能,典型算法有BPSK-like、Bump-Jump、ASPeCT、PCF等,下文对此进行详细讨论。

表1 GNSS多径抑制基带处理典型算法
1 传统多径抑制算法
GNSS多径信号对接收机信号处理的影响主要体现在两方面:
一方面,合成信号本身引入了载波和伪距测量值误差,直接影响跟踪环路对伪距等重要导航信息的解算。
另一方面,码跟踪环通过接收信号与本地参考信号的相关函数进行码相位识别,如图3所示,若接收信号中含有多径信号,会使得本地信号和接收信号的相关函数发生畸变,鉴相器在判断峰值位置时出现偏差,从而导致跟踪误差。
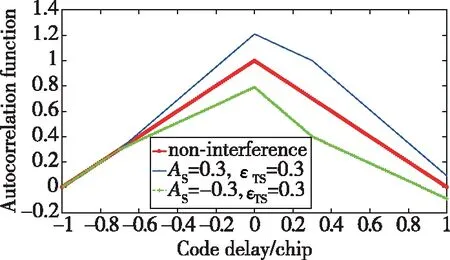
图3 合成信号和直达信号归一化相关函数Fig.3 Normalized correlation function of synthetic signal and direct signal
多径信号也会对载波跟踪产生影响,但由于多径信号对码环的影响远大于对载波环的影响,所以多径抑制算法研究多在码环。传统多径抑制算法从原理上主要分为参量式和非参量式,对于中长时延多径的抑制效果较好。
1.1 非参量式
非参量算法通过改进接收机的环路结构和鉴相器函数以降低对多径信号的敏感程度。1992年,文献[6]提出了窄相关技术,通过压缩码片间隔提高抗多径性能。1994年,文献[7]提出了ELS(Early Late Slope)技术,通过对相关函数两侧斜率进行估计,判断相关函数的畸变程度,跟踪精度比窄相关技术更高。1996年,文献[8]提出了Strobe相关器技术,文献[10]提出了脉冲间隙相关器(Pulse Aperture Correlator,PAC)技术。2002年,文献[11]提出了码相关参考波形(Code Correlation Reference Wavefo-rms,CCRW)技术,通过改变本地码波形获得理想的鉴相函数以抑制多径。2006年,文献[12]在CCRW的基础上提出了一种参考波形的设计方法,能够获得期望的相关函数。2009年,文献[13]提出了高分辨率相关器(High Resolution Correlator,HRC)。2012年,文献[14]提出了一种基于小波变换的多径抑制方法,利用小波变换判断伪码相关函数的奇异点,从而实现多径抑制。2013年,文献[15]在CCRW技术的基础上进一步研究了参考波形和闸宽对于多径抑制的影响。2018年,文献[16]提出了一种新的参考波形,对于高阶BOC信号具有良好的多径抑制效果。2020年,文献[17]提出了一种可满足多目标约束条件的参考波形设计方法。其中,Strobe相关器、PAC和HRC统称为Double-Delta技术,相关器间距相同时,该类技术的跟踪精度较窄相关技术更高。CCRW技术通过设计不同的参考波形可以达到本地相关器线性组合的效果,相较于Double-Delta具备更为优异的抗多径性能。非参量式算法的跟踪环路结构简单,跟踪速度较快,但多径性能受以下限制:1)受鉴相器性能和相关器间距的宽度限制等影响,不能完全消除多径影响;2)受前端带宽影响,前端带宽越窄时,相关峰越平,鉴相函数多径分辨率越低,需要增加带宽和信号采样频率,但会导致环路抗干扰和跟踪性能下降。
1.1.1 窄相关技术
卫星导航发展的早期,接收机码跟踪环的超前滞后相关器间距(Code Spacing)设置较大,一般为1个码片,能够减小初始捕获时间,但是会导致码环鉴相器函数单调范围较宽,跟踪精度较低,无法满足高精度定位需求。1992年,NovAtel公司提出了窄相关技术以提高跟踪精度。窄相关的码跟踪鉴相器是超前码与滞后码相减得到的,该技术通过减小相关器间距,提高鉴相器对峰值点的灵敏度,降低多径信号带来的误差,但是不能完全消除多径误差,具有一定局限性。一般而言,相关器间距越小,多径误差包络面积越小,抗多径性能越好,但随着相关器间距的减小,环路稳定性能变差,容易造成失锁等现象。
1.1.2 Double-Delta技术
Double-Delta技术通过两对相关器构建鉴相函数,主要包括HRC技术、Strobe相关器技术等。鉴相函数表达式为
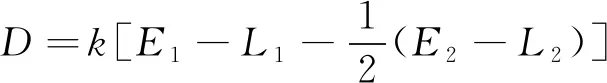
(1)
其中,、、、为两组超前滞后相关值,相距2,通过选取不同的值达到不同的效果。HRC技术选取的值为1,Strobe相关器则为2,两者抗多径性能相近。
图4中,表示伪码延迟,表示相关函数。由图4可知,相关器间距越小,Double-Delta的抗多径能力越强,相关器间距相同时,Double-Delta技术的抗多径性能要优于窄相关技术。
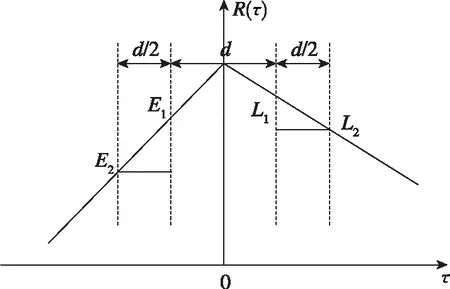
图4 Double-Delta技术Fig.4 Double-Delta technology
1.1.3 ELS技术
1994年,文献[7]提出了ELS技术,相较于Dou-ble-Delta技术,ELS技术同样是使用两组相关器,但是鉴相器设计的原理不同。ELS技术利用多径信号导致码相关函数在峰值两侧主瓣的坡度不同这一特性,对峰值两侧坡度进行估计,从而准确得出峰值的位置。
由图5可知,、、、为两组超前滞后相关值,ELS技术计算得到的多径误差为峰值两侧直线交点的横坐标,、、分别为相邻相关器之间的间隔,一般取==12,此时鉴相器表达式为
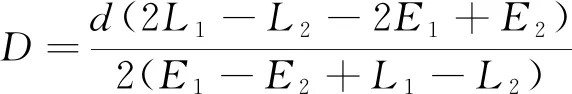
(2)
与窄相关技术类似,相关器间隔越小,抗多径性能越好。ELS技术依赖于两侧相关函数斜率估计的准确度,抗多径性能与窄相关技术相比有明显的提升,但是在信噪比较低时,斜率的估计往往不够准确,会造成较大的误差。
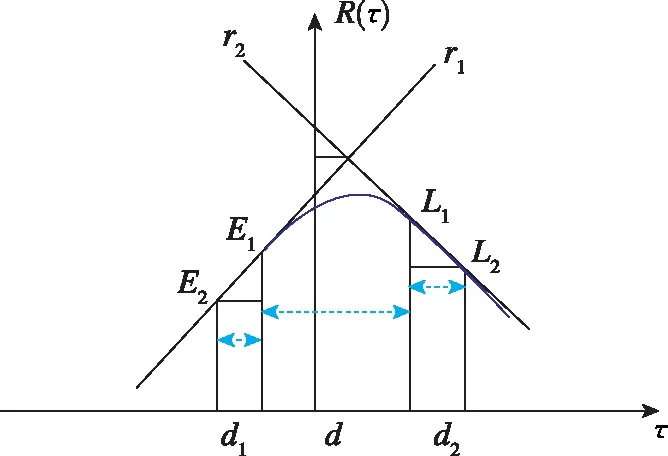
图5 ELS技术Fig.5 ELS technology
1.1.4 CCRW技术
2002年,文献[11]提出了CCRW技术,经过多次改进已较为成熟。该方法的原理是通过设计特殊的参考波形作为本地码,将其与接收信号相关后得到不同的鉴相曲线,抗多径性能与参考波形设计相关。基本参考波形主要有两类:第一类仅在码片变化处产生参考波形,第二类在每个码片边缘处产生并随之变化,部分波形的产生方式如图6所示。

图6 CCRW参考波形Fig.6 Reference waveform of CCRW
不同参考波形可以选择相同的鉴相函数,归一化表达式为

(3)
其中,、分别为同相、正交分量的即时相关值;、分别为同相、正交分量的参考波相关值。当参考波形为矩形码时,CCRW技术与窄相关技术等效,参考波形为时,CCRW技术与Double-Delta技术等效。通过选择不同的参考波,CCRW可以达到与其他非参量式算法类似的效果,无需增加额外相关器,环路简单。参考波的闸宽越小,多径抑制性能越好,参考波形为和时,抗多径性能比Double-Delta技术更优。
1.2 参量式
参量式算法的原理是通过大量的相关器获取多径信号的特征参数观测值,再通过估计算法得到多径参数最优估计值,最后剥离出直射信号。1995年,文献[20]提出了多径消除延迟锁相环(Multipath Estimation Delay Locked Loop,MEDLL)技术,通过估计多径参数有效抑制中长时延多径信号,但该方法计算量大,实时性较差。1997年,文献[21]提出了多径消除技术(Multipath Mitigation Technology,MMT),在MEDLL的基础上通过预先假设多径个数,简化多径模型,降低了计算量。2009年,文献[22]提出了Vision相关器(Vision Correlator)技术,通过精确测量码片过渡时刻的射频信号性能,提取清晰的码片过渡时刻波形,再剥离多径信号,多径性能相较于MMT得到进一步提高和优化。这类方法对中长时延多径误差的抑制效果好,跟踪精度高,但是由于需要估计多径信号并进行剥离,所以需要较多的相关器,跟踪环路结构较为复杂,计算量较大。除此之外,随着滤波和智能算法研究的深入,一些改进算法相继被提出。2017年,文献[23]采用遗传粒子滤波对多径信号进行估计,提高了多径估计的精度。2018年,文献[24]提出了基于差分进化(Differential Evolution,DE)改进粒子滤波的多径估计算法,提高了非高斯噪声下的估计精度。2019年,文献[25]提出了利用扩展卡尔曼滤波(Extended Kalman Filter,EKF)提高MEDLL的多径估计精度。同年,文献[26]利用信息论学习实现多径估计,该算法无需假设多径数目,能够快速实现参数估计。其他还有利用Newton法优化求解,加入TK算子降低计算复杂度等针对最大似然估计算法的改进。参量式算法需要估计多径信号的特征信息,跟踪精度相对于非参量式算法更高,但环路设计复杂,计算量较大。
接下来以MEDLL技术为例介绍参量式算法的实现过程,该技术是一种基于多径模型的参数估计方法,通过最大似然估计算法估计多径伪码延迟、载波延迟和幅值。
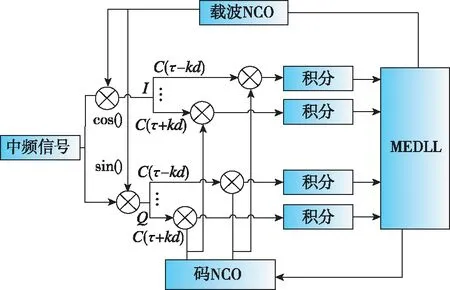
图7 MEDLL跟踪环Fig.7 Tracking loop of MEDLL
由图7可知,中频信号分别与本地载波sin()、cos()相乘分为(同相)分量和(正交)分量,之后分别进入2+1个相关器,每个相关器间隔为个码片。整个跟踪过程中含有大量待估参数,一般使用迭代求解。迭代过程分为参数估计、相关峰恢复和检测流程控制。其中,参数估计过程为假设输入仅有一路信号,估计该信号幅值、载波相位和伪码延迟;相关峰恢复过程为根据给定的幅值、载波相位和伪码延迟,输出估计的相关峰波形;检测流程为根据估计波形的残差预设多径路数,判断是否进行下一轮迭代。针对检测流程繁琐的问题,文献[29]提出了一种改进的MEDLL技术,该算法通过设定接收信号中最大路径数进行余量估计,能够有效提高直射信号的估计效率,但是依旧没有解决MEDLL需要大量相关器、计算量大的主要问题。MEDLL算法是目前最有效的多径检测和估计算法之一,跟踪精度较高,实时性较差,多径抑制性能主要受噪声影响。
1.3 传统多径抑制算法应用挑战:短时延多径
一般而言,以上方法可以在多数场合发挥较好的多径抑制作用,然而它们都有一个共同的缺陷,当面对短时延多径信号(多径延迟小于0.5码片)时,上述方法的抗多径性能会有一定的下降。短时延多径信号是多径信号中的一类特殊信号,两者具有相似的特性,但短多径信号的延迟更小。短多径抑制技术的难点在于短多径中直达信号的剥离和延迟的估计。关于短多径抑制算法的研究如下,2009年,文献[30]在HRC相关器中增加了修正因子以减小短多径误差。2010年,文献[31]提出了一种基于斜率的多径估计(the Slope-Based Multipath Estimation,SBME)方法,这种方法能够很好地抑制延迟小于0.35码片的短多径信号。2011年,文献[32]提出了一种新型码环路鉴相器(Short Multipath Insensitive Code Loop Discriminator,SMICLD),这种方法码环路简单,对短时延多径有较好的抑制效果。2012年,文献[33]在SMICLD的基础上进行改进,提出了MSMICD鉴相器,该方法计算量小,处理同相多径信号时性能优于SMICLD。2014年,文献[34]提出了改进窄相关的短多径抑制方法,在传统窄相关器的基础上,额外增加一个相关器用于对短时延多径误差进行定量估计并实时修正。同年,文献[1]提出了在Strobe相关器算法中引入修正因子,对码环鉴相器进行修正以抑制短多径。2019年,文献[35]提出了一种改进的对短多径不敏感的Strobe鉴相(Modified Short Multipath Insensitive Strobe Discriminator,MSMISD)算法,通过构造延迟相关值和设计反相多径补偿因子抑制短多径,相较于传统Strobe相关器抗多径性能更好。短延时多径抑制基带处理算法研究相对较少,大都是在传统长时延多径抑制算法的基础上进行改进,精度和抗干扰性能还有待提高。
2 新体制信号多径抑制算法
随着卫星导航定位系统的发展,现代化卫星导航系统通过采用二进制偏移载波(Binary Offset Carrier,BOC)调制和混合二进制偏移载波(Multiplexed Binary Offset Carrier,MBOC)调制解决频段拥挤的问题。BOC信号的数学模型表示如下
()=(-)cos(2π+)
(4)
=sign(sin(2π+))
(5)
其中,为信号幅值;为PRN码;为伪码延迟(单位是码片);为载波频率;为载波相位;为方波子载波;为子载波频率;决定子载波类型,取0时为sin-boc,取 12π时为cos-boc。
新体制信号从信号设计的角度减小多径误差,带来更高性能的同时提升了接收机设备的设计复杂度。现代化GNSS部分信号已采用BOC调制或在其基础上进行变形的调制方式,如北斗的B1C信号采用QMBOC调制,Galileo系统中E1信号采用CBOC调制和GPS中L1C采用TMBOC调制等。
新体制信号多径抑制算法针对于新体制信号设计,主要分为两类:一类是基于去模糊的多径抑制算法,另一类是针对不同信号特性设计的处理方法。
2.1 基于去模糊的多径抑制算法
BOC、MBOC信号虽然有着良好的抗多径性能,但是由于其自相关函数的多峰特性,容易导致跟踪环路发生误锁现象,在使用Strobe相关器、HRC等常用多径抑制算法时,在±0.5码片附近存在模糊点。为解决该问题,一般采用基于去模糊的多径抑制算法,这类方法由去模糊算法和传统多径抑制算法组成。首先通过去模糊算法解决BOC信号的模糊性问题,降低多径敏感度,再通过传统多径抑制算法进一步提高多径抑制性能。由于传统多径抑制算法上文已提及,接下来具体阐述去模糊算法的发展历程。
1999年,文献[38]提出了峰跳法(Bump-Jump),在传统BPSK跟踪方法的基础上增加了远超前和远滞后相关器,监测主峰两侧相关峰值,判断是否锁定在主峰,该方法需要积累较长的时间来完成失锁检测。2000年,文献[39]提出了非相干边带算法,通过对BOC信号进行单边带滤波消除多峰特性,但是该算法会造成信号能量的浪费,导致跟踪精度降低。2003年,文献[40]提出了一种基于子载波相关的去模糊算法。2004年,文献[41]提出了一种亚载波相位消除的去模糊算法,这类方法通过消除矩形波的方式获得单峰相关函数。2006年,文献[42]提出了BPSK-like算法,相较于非相干边带法的优点在于能够同时利用两个边带能量,提高接收机处理的卫星信号能量。2007年,文献[43]提出了信号相关边峰消除(Autocorrelation Side-Peak Cancellation Technique, ASPeCT)算法。同年,文献[44]提出了一种基于伪相关函数(Pseudo Correlation Function,PCF)的算法。2013年,文献[48]提出了一种MBOC信号去模糊算法,设计了双超前减滞后鉴相器去除MBOC信号的多峰性。2014年,文献[49]提出了一种基于PCF算法的CBOC信号去模糊算法,跟踪性能更优。2018年,文献[50]提出了一种基于CCRW算法的QMBOC信号去模糊算法,能有效消除多峰性,但由于闸波设计不便,具有一定局限性。
采用去模糊算法消除BOC信号的多峰性是后续使用鉴相器改进、参数估计等传统多径抑制算法的前提,同时可以通过构造特殊相关函数进一步提高整个算法的多径抑制性能。接下来对ASPeCT、PCF等典型去模糊算法进行介绍,这类方法通过多个互相关函数的非线性组合对原相关函数进行改进,重构的相关函数的多峰性大大减弱,从而减小了跟踪环路误锁的可能性。
2.1.1 ASPeCT算法
2007年,文献[43]提出了ASPeCT算法,经过多次改进已较为成熟。该算法是一种基于自相关边峰消除技术的跟踪算法,利用BOC信号与PRN码的互相关函数和BOC信号的自相关函数,对码环路相关结果进行重构,重构之后的相关函数为

(6)
其中,()是BOC信号的自相关函数;()是BOC信号和本地PRN序列的互相关函数;是调节因子,其取值影响ASPeCT相关函数中两个较小边锋的大小,需要根据应用的不同需求进行调整。
由图8可知,BOC(,)信号与本地伪码序列的互相关函数曲线关于原点中心对称,且存在两个峰值。这两个峰值的码相位延迟与BOC(,)信号自相关函数的两个边峰所在的码相位延迟相同,位于±0.5码片处。由于两侧峰峰值符号相反,ASPeCT算法利用平方运算消除符号对相关峰的影响,从而削弱侧峰对整个伪码跟踪环路的影响。ASPeCT算法构建的相关函数没有削弱主峰的幅值和宽度,保持了BOC(,)信号原有的特性,跟踪性能上优于传统的BPSK跟踪方法;但是该方法并不能完全消除自相关边峰,在主峰的两侧仍然留有两个较小的边峰,初始相位较大时可能会导致跟踪不稳定。针对该问题,文献[51]提出了改进ASPeCT算法相关函数,构建一个无边峰的相关函数,新相关函数的相关主峰相对于改进前更宽,这会导致环路的跟踪精度降低,但是新相关函数只有一个主峰,完全消除了边峰的影响,稳定性更好。ASPeCT算法构建的相关函数只能消除BOC(,)的边峰影响,对于BOC(,)信号和MBOC信号不适用。

图8 ASPeCT归一化相关函数Fig.8 Normalized correlation function of ASPeCT
2.1.2 PCF算法
2007年,文献[44]提出了PCF算法,经过多次改进已较为成熟,是一种通过构建伪相关函数实现无模糊跟踪的算法。PCF算法的主要原理为:在中频信号处理过程中构建两组本地参考信号()和(),分别与接收信号进行相关运算,相关函数为()和(),最后利用相关结果构建无相关边峰的伪相关函数,跟踪性能受宽度因子影响。相关函数为
()=|()|+|()|-
|()+()|
(7)
相关函数图像如图9所示。
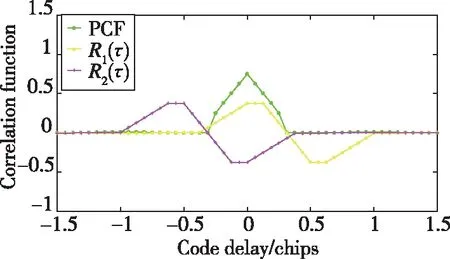
图9 PCF归一化相关函数Fig.9 Normalized correlation function of PCF
由图9可知,PCF算法能够彻底消除BOC信号的多峰性,同时利用合适的宽度因子获得更窄的相关主峰和更好的抗多径性能。2021年,文献[52]提出了一种子函数组合相关的无模糊跟踪算法,有效地适用于对BOC(,)和CBOC(6,1,1/11)信号的跟踪,但是与PCF算法相似,需要设计特殊的参考波形,组合函数在实现无模糊的同时会损失一部分跟踪性能。
2.2 其他处理方法
新体制信号多径抑制算法除了去模糊算法与传统多径抑制算法组合的方式之外,还可以根据信号结构特征设计特殊算法,提高信号利用功率和多径抑制性能。该类方法已实现工程应用的有联合跟踪、TM61跟踪算法和双重估计技术等。
2.2.1 联合跟踪
部分新体制信号为数据、导频分离的结构,数据分量包含电文信息,用于获取伪距和导航信息,导频分量仅有扩频码,不包含电文信息,从而增加了相干积分时间,精度更高。传统的多径抑制算法仅针对单路信号进行观测量的估计,这会造成有用功率的浪费,从而导致跟踪精度的降低,针对该问题,可以使用联合跟踪算法解决。2002年,文献[54]针对L5信号提出了鉴相器和滤波器层面的联合跟踪方法,并研究了该方法的适用性。2010年,文献[55]针对E1信号提出了数据/导频联合捕获跟踪算法,提高了捕获跟踪的稳定性。2011年,文献[56]提出了不同权重的非相干和相干数据/导频联合方法,提高了信号的利用率。同年,文献[57]针对L5信号提出了三种复杂度不同的联合跟踪方法,分别为相关器输出联合、鉴相器输出联合和滤波器输出联合。2013年,文献[15]提出了联合多径抑制算法,将CBOC信号的导频和数据通道利用码参考波形技术实现多径抑制,再进行非相干合并消除BOC(6,1)分量的影响,达到了该信号的多径抑制极限。2018年,文献[58]针对B1C信号,采用导频辅助数据联合跟踪和数据/导频幅值联合跟踪,提高了跟踪的精度和稳定性。2019年,文献[51]分析比较了三种联合跟踪算法的跟踪精度和抗多径性能,为以后的研究提供参考。2020年,文献[59]提出了一种B1C信号的无模糊捕获算法,采用数据/导频非相干组合的捕获策略,实现了B1C信号的无模糊捕获。同年,文献[60]提出了一种基于EKF的数据/导频联合跟踪方法,在联合跟踪模型的基础上引入卡尔曼滤波器,进一步减小跟踪误差。
由图10可知,联合跟踪方式分为相关器、鉴相器和滤波器三类。相关器联合通过数据和导频相关积分进行组合,需要判断电文与二次码符号,环路结构最简单,但是在低载噪比时符号判断受影响,从而导致精度下降。鉴相器联合通过信号发射功率比对数据和导频鉴相器输出进行加权组合,环路结构相比相关器联合更复杂,在低载噪比环境下精度更高。滤波器联合通过信号发射功率比对数据和导频环路滤波器输出进行加权组合,复杂度最高,在低载噪比环境下精度最高。

图10 联合跟踪结构Fig.10 Combined tracking structure
2.2.2 TM61跟踪算法
TM61跟踪最早是由ENAC的信号处理实验室针对于TMBOC(6,1,1/11)信号提出的。2007年,文献[61]将其用于跟踪CBOC(6,1,1/11)信号。2019年,文献[51]研究了TM61跟踪在QMBOC调制信号上的应用。
由图11可知,TM61算法中延迟锁定环P(即时)支路将BOC(1,1)分量与接收信号进行相关运算,利用BOC(1,1)信号的高功率特性获取接收信号的数据信息;E(超前)和L(滞后)支路采用接收信号与本地BOC(6,1)信号进行互相关,利用BOC(6,1)信号的高精度特性对接收信号进行跟踪。该算法充分利用了BOC(1,1)信号和BOC(6,1)信号的特性,抗多径能力强。但是该算法有两个缺点,一是TM61跟踪是仅适用于BOC(1,1)信号和BOC(6,1)信号复用调制的信号,具有一定局限性;二是由于该方法并没有充分利用MBOC信号的能量,跟踪精度低于使用复用信号的相关结果。
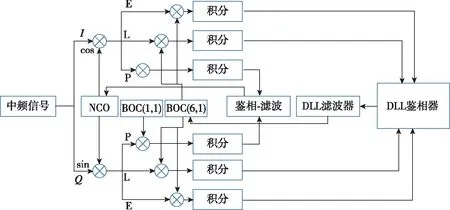
图11 TM61算法跟踪环路Fig.11 TM61 tracking loop structure
2.2.3 双重估计技术
由式(4)、式(5)可知,BOC调制的原理是在原有BPSK调制的基础上,加上一个二进制副载波对BPSK信号进行二次扩频。针对该类信号,2008年,文献[66]提出了双重估计技术(Dual Estimate Technology,DET),分别使用码环和副载波环对伪码和副载波进行跟踪。2018年,文献[67]提出了一种基于改善DET的多径抑制算法,设计了一种DET双环交互互相关函数,多径抑制性能高于传统DET算法。
DET方法的原理是将本地伪码信号和本地副载波信号分离,分别进行相关。从伪码层面看,相关函数与BPSK伪码相关函数形状类似,具有单峰性,但是精度较低。从副载波层面看,精度较高,但是具有模糊度。通过两者的非线性组合可以取得精度较高且无模糊度的结果,DET的性能由副载波跟踪精度决定。目前,副载波跟踪方式可以分为两种:一种是延迟锁定环跟踪(Subcarrier Delay Loc-ked Loops,SDLL)方式,该方式计算复杂度较低,要求的硬件资源少,考虑到应用实现难度,一般用于伪码速率较低或BOC阶数较低的信号;另一种是锁相环跟踪(Subcarrier Phase Locked loops,SPLL)方式,对软硬件要求较高,在跟踪精度和抗多径性能上相对于SDLL具有优势,一般适用于伪码速率较高或BOC阶数较高的信号。
3 结论与展望
目前,GNSS多径抑制基带处理算法相关研究如图12所示,按信号体制可以分为传统多径抑制算法和新体制信号多径抑制算法。传统多径抑制算法主要针对于BPSK信号,分为非参量式和参量式,其中非参量式算法通过改进鉴相器,降低其对于多径的敏感性,提高抗多径性能,该类方法环路简单,计算量较小;参量式算法需要估计多径信号的特征,跟踪精度较高,计算量较大。新体制信号多径抑制算法针对于BOC、MBOC信号,按实现方式分为两类:第一类是基于去模糊的多径抑制算法,这类方法适用范围较广,首先去除信号多峰性,然后改善传统算法的多径抑制性能,进一步提高跟踪精度;第二类是针对特殊信号结构的处理算法,此类方法根据不同的信号结构进行设计,提高信号在跟踪过程中的利用功率,从而提高跟踪精度,相较于第一类方法精度更高,但适用范围更窄。

图12 多径抑制基带处理算法框架Fig.12 Framework of multipath mitigation baseband processing algorithm
由上述分析可知,GNSS多径抑制基带处理算法相关研究面对的挑战主要有两方面:一方面是越来越复杂的应用场景对多径抑制算法鲁棒性、快速性、准确性提出更高的要求;另一方面是不断发展的卫星信号体制使得多径抑制算法需要向针对性、高效性的方向发展。随着卫星信号设计和信号处理技术的不断发展,多径抑制基带处理算法也需要随之不断进步,从而进一步提升卫星导航系统服务性能和服务质量。在此基础上,对GNSS多径抑制基带处理算法研究前景进行展望:
1)改善算法性能:
①提高多径抑制算法的性能,提高Double-Delta、MEDLL、ELS等算法的跟踪精度和计算效率,合理改进算法使其满足应用需求。对于新体制信号,一方面需要加强去模糊算法的研究,使其在达到无模糊的同时保留原信号的良好特性,如主峰宽度、信号强度等,从而进一步提升多径抑制性能;另一方面,针对信号结构进行新型跟踪算法的研究,如数据/导频联合跟踪、TM61跟踪算法等,提高新体制信号的能量利用率,发挥新体制信号的优秀性能。
②改善特殊多径的抑制性能,一是加强短多径抑制算法研究,随着卫星应用越来越广泛,特别在复杂城市环境中,多径信号往往是近距离和短时延的,使得短多径抑制技术具有较高的研究价值;二是加强高阶BOC信号多径抑制算法研究,目前BOC多径抑制技术多集中于低阶BOC信号,高阶BOC信号的研究相对较少,高阶BOC信号的带宽较大,其自相关函数的相关峰窄而且非常密集,有的甚至存在一定的非对称性,给跟踪和多径抑制带来挑战,如Galileo E1频点和北斗B3频点的BOC(12,2.5)等。
2)多源信息融合:结合卫星导航的发展趋势,将信息融合技术应用于基带处理算法解决多径问题,例如加强矢量跟踪技术的研究,矢量跟踪算法的原理是将各通道的鉴相器误差及其他辅助信息(如惯导)输入到导航滤波器,再生成环路控制量调节本地NCO,在高动态、遮挡和空旷的环境下,相较于标量跟踪算法具有更高的跟踪精度和多径抑制能力,目前应用主要受结构复杂和计算量大的限制,可以从滤波算法角度出发进行改善。
3)算法应用优化:加强新播发信号多径抑制算法的应用研究,通过改进与新播发信号结构类似的多径抑制算法,快速地实现新信号的精确跟踪,提高算法的适用性,如早期北斗B1C信号的多径抑制算法的研究可以借鉴GPS的TMBOC信号和Galileo的CBOC信号,加快产品化进程。

