基于PSO-ELM的卫星导航欺骗式干扰检测

周 彦，王山亮，杨 威，易 炯，张世仓，王冬丽，蔡成林

(1. 湘潭大学自动化与电子信息学院，湖南湘潭 411105；2. 长沙海格北斗信息技术有限公司，长沙 410003；3. 中国航空工业集团公司雷华电子技术研究所，无锡 214000)

0 引言

随着卫星导航系统的飞速发展，卫星导航系统业已成为人们日常生活和生产活动中不可缺少的一部分。如今，卫星导航系统已服务于交通、电力、金融、通信等各行各业，并赋能各行业提质升级，这显示出卫星导航系统巨大的应用价值。然而，卫星导航系统在使大众生活更加便利的同时，也带来了一定的潜在威胁。由于导航卫星距离地面2万～3万km，卫星信号到达地面时非常微弱。因此，接收机非常容易受到有意或无意的干扰。而正是由于干扰的存在，使得接收机无法工作,或者即使捕获、锁定卫星信号，解算出来的位置速度时间(Position Velocity and Time，PVT)精度也会很低。更甚者，当不法分子利用发射设备发射虚假的卫星信号并被接收机捕获时，接收机最终解算出虚假的PVT结果，严重情况下将导致社会关键基础设施瘫痪、军事行动失败等后果。

近些年，全球频频发生的卫星干扰事件也证明了卫星信号的脆弱性。2011年12月，伊朗军方利用全球定位系统(Global Positioning System，GPS)欺骗设备成功捕获一架美军隐形无人侦察机RQ-170。2017年6月22日～24日期间，在黑海作业的20多艘船只受到了大规模诱骗攻击，其GPS错误地将船舶定位在了距航行位置数英里外的机场。2019年11月，北约多国联合部队举办的三叉戟军事演习期间，芬兰北部地区以及东北部地区GPS信号出现了明显的干扰情况，使得大批民航客机上的航电设备受到干扰滞留机场无法起飞，芬兰空军原本的军事演习计划也受到了很大的影响。

以上案例说明，有针对性地进行卫星干扰，其后果往往不堪设想。而且随着软件定义无线电技术和开源导航模拟软件的不断发展，欺骗的实施成本和技术门槛也逐步降低。因此，卫星导航欺骗式干扰检测的研究对卫星导航安全、可靠地提供服务具有十分重要的意义。

国内外学者对卫星导航欺骗干扰检测进行了相关研究。常见的欺骗干扰检测方法有：对导航信号进行加密认证处理,如文献[3-4]采用扩频码加密技术，文献[5-6]采用导航电文加密技术，但是由于加密信息是一项庞大的工程，在短期内很难实现;基于空间处理的欺骗干扰检测，利用空间处理技术估计接收信号的空间特征，识别那些空间相关的信号，但是该方法增加了天线阵元，提高了系统硬件成本，且实时性差;基于基带数字信号处理的欺骗干扰检测，该类检测方法主要是对信号功率和信号质量进行检测,但是对于信号强度较大的欺骗信号检测效果不尽人意;基于定位导航结果的欺骗干扰检测，主要通过高精度的辅助设备(惯性导航系统、芯片级原子钟等)测得数据信息与全球导航卫星系统(Global Navigation Satellite System，GNSS)接收机测得数据信息进行一致性比较以实现欺骗检测，这大大增加了检测成本，不宜大规模应用。

上述几类检测技术仅利用一个参数检测欺骗干扰的存在，具有一定的局限性，综合考虑多个参数信息可以弥补单一参数的不足，将多个参数作为神经网络的特征输入，构建分类器，通过对信号分类达到检测欺骗干扰的目的。本文首先给出了信号模型，信号经接收机处理计算得到所用的特征参数，随后给出了检测欺骗干扰的方法和优化过程，最后通过实验验证了该方法的有效性。

1 卫星信号干扰模型

1.1 干扰建模

假设时刻，接收机接收到的信号为(), 则()可以写成

()=()+()+()

(1)

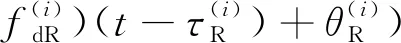
(2)

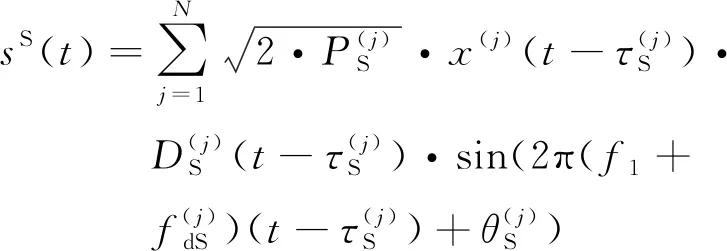
(3)

假设时刻，接收机解算出的伪距值为()，则()可以写成

()=()+Δ()

(4)

()=()+·(δ()-δ()+

δ()+δ())+

(5)

Δ()=()-()+·Δ()

(6)

其中，()、Δ()分别表示不存在欺骗干扰时测得的真实伪距值和存在欺骗干扰时附加的伪距偏差量；()表示卫星与接收机之间的真实距离；表示光速；δ()、δ()、δ()、δ()分别表示接收机钟差、卫星钟差、电离层时延和对流层时延；表示测量噪声；()表示卫星到干扰源与干扰源到接收机的距离和；Δ()表示转发过程中信号增加的时延。

1.2 特征参数选择

由1.1节可知，当欺骗干扰源发射欺骗信号并被目标接收机捕获、跟踪时，会造成载波相位、载波多普勒频移、信噪比等信息发生异常突变。在进行最终解算时，也会造成伪距等信息发生突变。本文将观测文件中的伪距信息、载波相位观测值、载波多普勒频移和信噪比作为特征输入参数，记为={，，，}。

(1):伪距

伪距(Pseudorange)是指在卫星导航定位过程中，地面接收机到卫星的大概距离。伪距定义为

()=·(()-(-))

(7)

其中，()表示伪距；表示光速；()表示GPS时间为时的接收机时钟；(-)表示卫星信号的发射时间。

(2):载波相位

载波相位是指在同一接收时刻基准站接收的卫星信号相位相对于接收机产生的载波信号相位的测量值。载波相位定义为

=-

(8)

其中，表示载波相位测量值；表示接收机复制载波信号的相位；表示接收机接收到的卫星载波信号相位。

(3):载波多普勒频移

当发射源与接收机之间存在相对运动时，接收机接收到的发射源发射信息频率与发射源发射信息频率不同，这种现象称为多普勒效应，接收频率与发射频率之差即为多普勒频移。载波多普勒频移定义为

(9)

其中，表示载波多普勒频移；、分别表示接收机速度和卫星速度；表示卫星在接收机处的单位观测矢量；表示载波波长。

(4):信噪比

信噪比就是信号功率和噪声功率的比值，常表达成分贝的形式，一般用于衡量信号的质量，信噪比定义为

(10)

其中，SNR表示信噪比；、分别表示信号功率和噪声功率。

2 算法原理

2.1 ELM算法

极限学习机(Extreme Learning Machine，ELM)是架构在单隐层前馈神经网络基础上的算法，其网络框架如图1所示，其输入权值和偏置均采用随机赋值的方式，并在最小二乘准则下，利用Moore-Penrose广义逆计算输出权值。因此，相较于传统的基于梯度下降学习理论的神经网络，ELM具有快速收敛、不易陷入局部极值等优点，适合对数据繁琐的导航观测数据进行检测。ELM算法描述如下。

图1 ELM网络结构Fig.1 ELM network structure

给定包含个样本(，)，=1,…,的数据集，其中，=[1,2,3,4]∈表示第个样本的特征参数，是跟样本对应的类别标签，类别标签标为“1”和“2”分别代表真实信号和欺骗信号。对于一个有个隐层节点的单隐层神经网络可以表示为

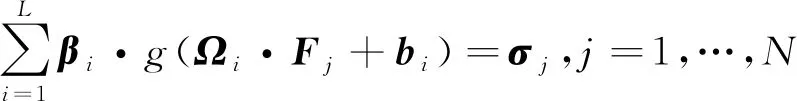
(11)

其中，()为激活函数；=[1,2,3,4]为输入权重；为输出权重；为第个隐层单元的偏置；·表示和的内积。

ELM的学习目标是使得输出的误差最小，可以表示为

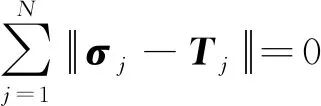
(12)

即∃,,，使得

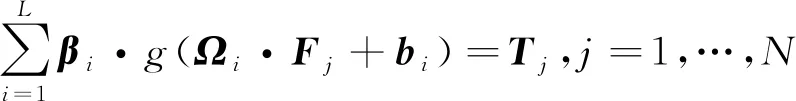
(13)

矩阵表示为

·=

(14)

其中，表示隐层节点的输出；表示输出权重；表示期望输出。

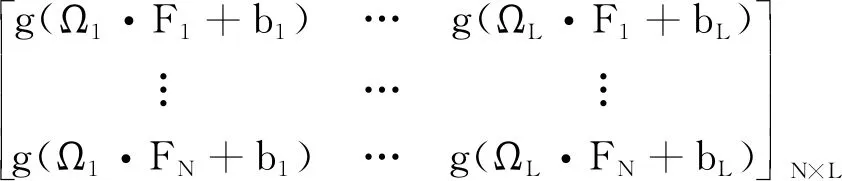
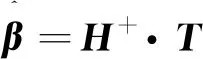
(15)

其中，是矩阵的M-P广义逆矩阵。

2.2 PSO-ELM算法

虽然ELM不需要迭代调整就可以解算出神经网络的输出值，但是由于随机生成输入权值矩阵和隐层节点阈值，这就不可避免会产生隐层节点冗余或不足、对未知输入参数识别能力较弱等问题，从而使得最终生成的网络模型产生较差的分类效果。故而，本文结合粒子群优化(Particle Swarm Optimization，PSO)算法对ELM中的输入权重和偏置进行寻优，建立PSO-ELM神经网络模型以提升分类效果。

PSO算法是一种模拟鸟群觅食行为的群体智能优化算法，其本质是基于粒子群中的个体对信息的共享特性来获得问题的最优解。假设在一个维空间中，每个粒子表示为=(1,2,…,),每个粒子的好坏通过适应度函数值进行判断，通过跟踪全局最优解和个体最优解来更新粒子位置和速度，并最终实现全局寻优的目的。若粒子的速度表示为=(1,2,…,)，那么粒子的速度和位置的迭代公式如下

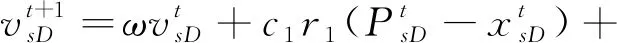
(16)

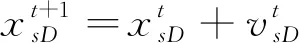
(17)

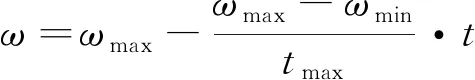
(18)

其中，、分别为惯性因子的最大值和最小值；、分别表示最大迭代次数和当前迭代次数。

将ELM中的输入权重和隐层节点偏置作为粒子群算法的粒子，将ELM训练集的分类错误率作为适应度函数，计算每个粒子的适应度值，比较并不断迭代更新粒子的速度和位置，直至错误率达到最小或达到最大迭代次数，最终获得经过PSO的ELM网络参数。

基于PSO-ELM的卫星导航欺骗式干扰检测流程如图2所示。

图2 基于PSO-ELM的卫星导航欺骗干扰检测流程Fig.2 Satellite navigation deceptive jamming detection process based on PSO-ELM

3 实验仿真

3.1 实验数据

本研究实验场景为湘潭大学信息楼顶楼，使用有源天线GNSS SMA通过软件定义无线电RTL-SDR V.3 RTL2832U和开源GNSS-SDR程序采集数据，设置RTL-SDR采样中心频率为1575.42MHz，I/Q支路的采样频率为2.048MHz，共采集43589组数据，每组数据有4个特征属性，将数据集中的80%作为训练集，用于训练模型，另外20%的数据作为测试集，用于测试其学习效果，具体如表1所示。

表1 实验数据集

此外，由于观测数据单位不一，有些数据变化范围较大，有些数据变化范围较小，这可能导致神经网络训练时间长、收敛慢，更有可能使得输入属性的作用权重不同，从而影响训练结果。因此，在将数据输入到ELM训练之前，先进行了标准化处理，从而将有量纲的数据转化为纯量，以保证数据间的可比性。本文采用Z-score标准化对特征数据进行处理，经过处理后的数据的均值为0，标准差为1，标准化公式如下

(19)

其中，和分别为标准化后和原始数据；和分别为数据均值和标准差。

3.2 参数优化研究

通过标准ELM搭建卫星导航欺骗干扰检测模型时，只需要在初始化时选择隐层节点个数和激活函数()便可以解算出输出权值矩阵。在实际应用中,一般远小于样本数，当过小时会使得神经网络模型的分类效果很差;当选取较大时，一方面会增加模型的时间和运算成本，另一方面也容易造成过拟合现象。图3对比了三种常见的激活函数sigmoid、sin和hardlim在不同的隐层节点下，对最终分类准确率的影响。

图3 不同激活函数下隐层节点数对ELM分类性能的影响Fig.3 Influence of the number of hidden layer nodes on ELM classification performance under different activation functions

由图3可以发现，sigmoid函数和sin函数的分类性能接近,且优于hardlim函数的分类效果，当隐层节点增至22时,分类准确率近似达到100%。故而，对于未优化的ELM卫星导航欺骗干扰检测模型，激活函数选择性能较好的sigmoid函数。同时为了方便比较，接下来的实验仿真都选择sigmoid函数作为激活函数。

与此同时，研究了3组不同粒子数目对PSO-ELM模型迭代过程的影响，如图4所示。3组粒子数目分别为20、50、100。

由图4可知，当粒子数为100时，随着迭代次数的增加，适应度值比另外两条曲线更快趋于稳定。

图4 不同PSO粒子数对PSO-ELM迭代过程的影响Fig.4 Influence of different PSO particle numbers on PSO-ELM iterative process

对于PSO-ELM分类器，设定粒子群数目=20，==2，=09，=02，=20,仿真结果如图5所示。

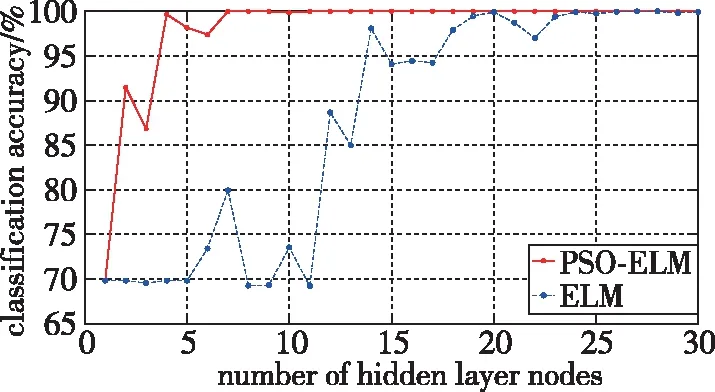
图5 PSO-ELM和ELM隐层节点数对分类准确率的影响Fig.5 Influence of the number of hidden layer nodes of PSO-ELM and ELM on classification accuracy

由图5对比可见，采用PSO-ELM的网络参数，能够以更少的隐层节点获得更高的分类准确率。

3.3 检测结果分析

首先仿真了在不同数量和不同特征组合输入下PSO-ELM模型的检测性能，如表2所示。从表2可以发现，随着特征参数输入数量的增加，PSO-ELM模型的检测性能总体上也越来越好。

表2 不同特征组合下PSO-ELM的检测性能

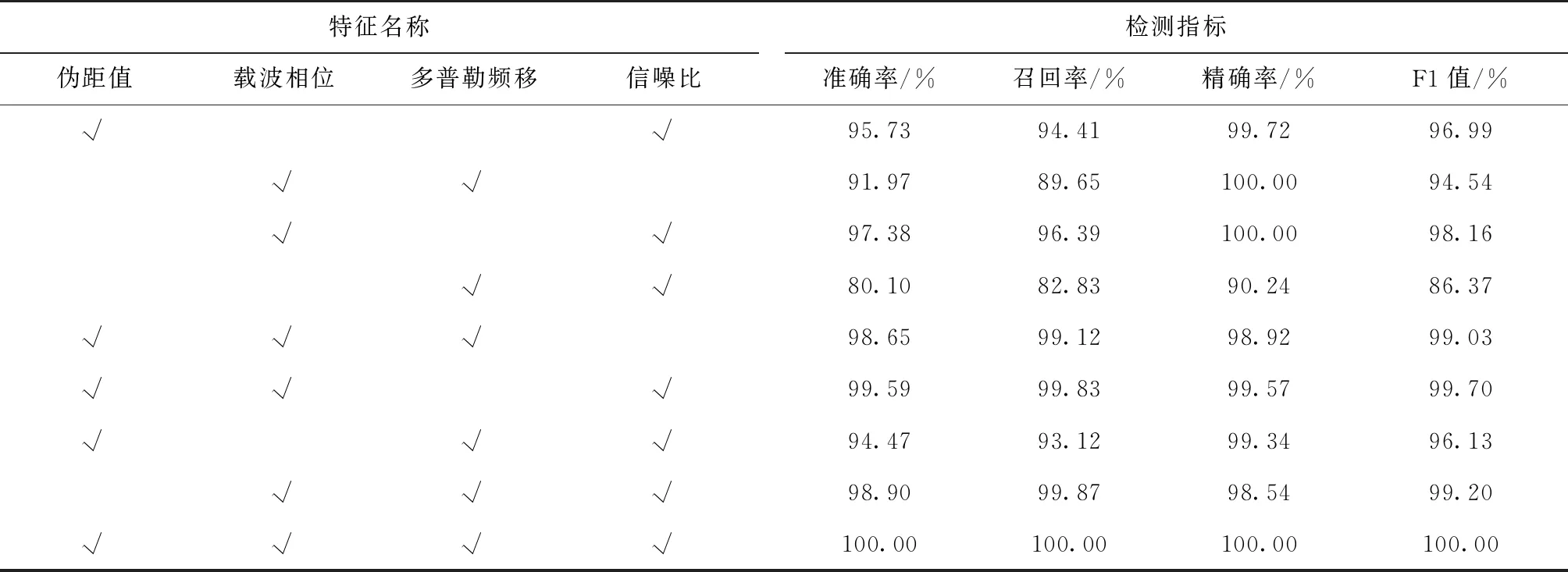
续表

经过对参数优化分析，同时为了方便对比，之后的实验将隐层节点数统一设为15，粒子群数目定为20，=1，==2，=09，=02，=20。由表1可以发现，卫星导航数据集正负类是不平衡的，故而为了更好地反映分类效果，分别给出了ELM和PSO-ELM的混淆矩阵，如图6和图7所示，并计算出了分类评价指标准确率、召回率、精确率和F1值如表3所示。由图6、图7和表3可以发现，ELM经过PSO优化网络参数后，神经网络模型的分类效果显著提升。

表3 ELM和PSO-ELM模型分类性能比较

图6 PSO-ELM模型混淆矩阵Fig.6 Confusion matrix of PSO-ELM model

图7 ELM模型混淆矩阵Fig.7 Confusion matrix of ELM model

图8给出了PSO-ELM模型的迭代曲线，结果可见，经过12次迭代后，PSO寻得最优解，此时的适应度值为0。

图8 PSO-ELM算法的迭代曲线Fig.8 Iterative curve of PSO-ELM algorithm

图9给出了测试集上逐个样本PSO-ELM分类结果与实际类别的对照，由于测试数据较多，为了测试结果在可视化后能够更明显地发现错误分类，对测试后的分类结果进行了升序处理。由测试结果图9可以发现，PSO-ELM网络模型具有100%的分类准确率，能够很好地满足卫星导航欺骗干扰检测的应用要求。

图9 PSO-ELM分类测试结果Fig.9 Classification test results of PSO-ELM

4 结论

针对卫星导航欺骗式干扰检测问题，本文提出了一种基于PSO-ELM的卫星导航欺骗干扰检测方法，通过PSO算法优化ELM模型的输入权值和隐层偏置，并利用采集的数据集对ELM和PSO-ELM模型进行仿真测试和参数优化研究。得到以下结论：

1)仿真结果发现，相较于ELM模型，PSO-ELM模型能够以更少的隐层节点数目达到更高的分类精度。

2)仿真结果发现，随着输入特征数量的增多，PSO-ELM模型的检测性能也随之提升。

3)PSO-ELM模型的分类准确率和精确率都为100%，表明本文提出的方法在卫星导航欺骗干扰检测上具有很好的可行性和适用性。