城市公共空间三维路径系统寻径方法与应用*——以淮安井神盐化工业区更新改造为例

1 研究背景

1.1 城市公共空间中的路径探索问题

随着我国经济社会的快速发展，城市空间需要提供更丰富多样的宜居空间[1]，不断涌现的大型商业综合体、大型游乐中心、大型博览园区等公众开放空间，成为宜居城市环境的重要空间载体[2，3]。随着购物、观景、休闲、交往活动等公共活动越发复合，城市公共空间的空间形式和交通流线亦趋于复杂，通达、便捷、安全的路径系统规划设计也就变得愈发重要。一方面，复杂而复合的公共空间中，路径系统应使人流便捷且不迂回地到达公共空间中的每一处节点，为人的活动提供便利；另一方面，路径系统应与各功能空间探访和使用的先后顺序相契合[4]；同时，路径系统还应具有安全疏导人流与组织交通流线的功能，以满足公共空间的使用安全需求。因此城市公共空间中的路径系统规划是一个需满足多目标需求的路径探索问题。复杂的空间形式与多目标的空间使用需求，强调了公共空间中路径系统合理规划的重要性，也引发了路径系统设计复杂度的成倍级增加。

面对高度复杂的路径系统设计问题，人工的设计方法会带来大量重复工作，效率较低，且难以寻求最优解。随着计算机技术在建筑学领域的发展[5]，路径规划这一建筑学典型问题的数理转化目标逐步明确，并有合适而清晰的算法支撑[6，7]，因此设计者开始运用程序算法来研究与解决部分简单的路径规划问题。

1.2 算法辅助下的路径规划研究

常见的寻径算法，例如计算机图形学中在网络范围内探索两节点之间最短路径的算法等，在交通导航、游戏地图寻径、机器人智能寻径等领域已多有应用[8]。近年来，在面对城市空间中的复杂路径系统问题时，此类算法同样为路径规划提供了一定的技术策略。周俊杰以Dijkstra算法为基础提出了一种改进的城市分层分区路径规划算法并将之应用于城市路径选择问题中[9]。马卡里耶（Makariye）用Dijkstra算法尝试解决城市交通的周期性变化带来的路径规划问题，拓展了最短路径算法的应用领域[10]。李昊则系统性地归纳了多种寻径算法在城市道路生成设计中的可能性，为相关研究做了方法性总结[11]。胡震宇在对西安碑林历史街区的研究中，结合高密度历史街区的现状和实际应用，利用A＊寻径算法解决了街区更新改造中的游览道路生成问题，并将其拓展至高密度历史街区的室外消防系统的生成设计中[12，13]。目前上述相关研究成果大都以二维路径探索的方法探讨平面上的最短路径问题，然而在实际的城市公共空间中，由于场地大都包含了复杂的地形条件和景观资源、众多建筑本身又具有复合的功能空间，使得其路径规划问题不再是二维层面上的最短路径问题，而是三维空间中需考虑多重影响因素的路径系统探索问题。

并且，以上研究仅尝试使用寻径算法解决了城市路径规划中的部分问题，未能结合实际的设计项目形成串联场地分析与路径方案的完整工作流程，场地分析无法为设计工作提供明确依据，设计成果也无法从场地分析中得到有效反馈。目前，已有研究者在面对设计问题时尝试通过数据的传递建立“数字链”闭环，以数据信息串联形态分析，方案设计乃至实际建造的全过程。李飚、郭梓峰等从算法理论、模型搭建和实际项目应用等多方面阐述了“数字链”系统在串联设计与建造的连续性上的特征与优势[14，15]。唐芃、王笑等则在宜兴丁蜀古南街这一传统聚落的保护与更新设计中，建立了“数据收集-特征提取-生成设计”的数字链闭环，并具体介绍了数据传递在二维立面风貌和三维空间肌理的研究中发挥的作用[16，17]。以上研究通过构建“数字链”工作流程，提升工作效率的同时，增强了分析与设计工作之间的联系，使设计工作能够以分析结果为依据。“数字链”系统思维应用于路径规划设计中同样能够建立场地分析到路径方案设计之间的数据衔接，并快速获得分析结果指引下的合理设计结果。

笔者在淮安井神盐化工业区城市更新设计中遇到了上述三维路径系统的探索问题。本研究即以这一实际设计项目为例进行了三维路径探索算法模型的搭建，并将路径探索结果与数字化建模工具进行数据连通，以支持设计师的深化设计。本研究的重点在于：1）提取该项目中路径规划设计的场地条件，转译为程序语言，建构了包含空间影响因素评价值的三维寻径网络，运用Java语言编程开发工具IntelliJ IDEA建构对应的三维寻径算法模型，实现了三维路径系统的寻径探索；2）将寻径结果与Grasshopper数字化建模工具之间进行数据衔接完成了实际项目的设计深化，形成了从场地分析到算法寻径到方案深化的完整的“数字链”工作流程。

2 寻径算法模型与“数字链”工作流程的构建方法

2.1 受场地空间要素影响的寻径算法模型

目前应用较为广泛的最短路径算法有Floyd算法，Dijkstra算法，Bellman-Ford算法，SPFA算法等[18]，这些算法在适用性和时效性上有着较大差别（表1）。

表1 目前应用较为广泛的最短路径算法的特征对比

由于城市大型公共空间中的三维路径系统可以看做是无负权网络中的多条单源最短路径，因此研究以Dijkstra算法为原型进行算法模型的构建。Dijkstra算法的基本原理为基于一个点阵网络，从起点开始每次遍历到起始点的总“移动代价”最小且未访问过的顶点的邻近点，直至找到终点后，所形成的起点与终点之间路径上所有点的移动代价之和最小的路径即为最短路径，其计算方法如公式1所示（其中，Ca为该路径上各寻径点的移动代价之和，Ci为第i个寻径点的移动代价，n为路径上寻径点的总数）：

因此建构算法模型的第一步，即如何将实际设计中的场地条件转译为可供算法运行的寻径网络。研究通过Java语言编程，在场地范围内建构了XYZ三坐标方向的三维网格，网格上的每个节点均为一个寻径点，形成寻径算法所需的点阵。同时通过DXFImporter工具包，读取项目所提供的场地dxf文件中的分图层信息，将场地中的建筑、地形、景观等要素转换到Java语言环境的数学模型中，为寻径网络中的每个寻径点赋予对应的地理信息。

避开场地中的建筑与其他障碍物是路径规划设计的基本要求，因此基于场地构建的寻径网络也应区分出场地中的障碍物。程序算法在为寻径网络中的每个寻径点赋予地理信息的过程中会判断该点与障碍物的相对位置，对于位于建筑体量中或其他不适宜路径通过位置的寻径点，算法会将这些寻径点的“移动代价”值设为无限大，以保证该点不会被路径选择，完成避障功能。

对于本研究所面临的城市设计问题，还需要将影响路径规划设计的多个空间影响因素融合进寻径网络中，使寻径网络中可以通过的每个寻径点的“移动代价”值能够反映多个空间影响因素的综合影响结果。在本研究中，每个寻径点的“移动代价”值Ci由三个影响因素评价值的加权和组成，分别是反映该点人的空间体验的评价值M1；反映该点建设成本差异的评价值M2；反映该点景观价值的评价值M3。其计算方法如公式2所示（其中，W1、W2、W3分别为空间体验、建设成本与景观价值评价值对应的权重，W1+W2+W3=1）：

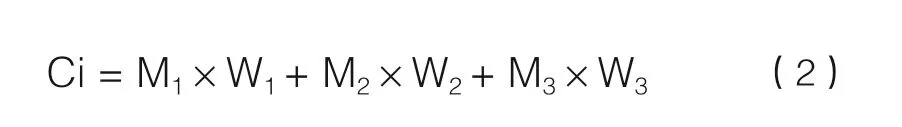
M1、M2、M3的评价值越高，反映了该寻径点在当前因素影响下越不利于路径通过。三个评价值均由对应的数个二级影响因素计算得来，如表2所示。例如对于建设成本，程序算法会根据寻径点所在的地形位置信息及高度判断建设的难易程度，所在位置不利于建设三维路径（例如水面上方）的寻径点，其建设成本评价值也就更高。对于空间体验与景观价值，同样采取类似的量化评价方法，将建筑学问题转化为可进行数学计算的二级影响因素，进而得到相应的评价值。

表2 寻径点综合“移动代价”的影响因素

在这个三维寻径网络中，寻径点的综合“移动代价”值不再仅仅以路径最短为目标，而是反映了三维路径能否通过该点以及通过该点时基于空间体验、建设成本、景观价值等影响因素的综合移动成本。同时，算法模型设定设计师可根据设计需要，调整各影响因素的权重，使寻径网络可用于寻找倾向性不同的寻径结果。

寻径网络构建完成后，还需对寻径算法进行改写。相比于传统的Dijkstra算法，本研究编写的寻径算法的两大不同之处在于：1）需要将算法拓展到三维层面上使其在三维寻径网络中合理运行，2）使新算法具有最佳优先搜索的高效性2），以应对算法拓展到三维层面后巨大的运算量。

沿用Dijkstra算法的基本原理，本研究通过对算法中选取后续点的函数进行改写，使任意点在三维方向上的临近点均可被纳入计算，从而使算法能够在已构建的三维寻径网络中探索综合“移动代价”值之和最小的路径系统。面对同一设计场地，三维寻径网络使寻径点的总数大量增加，给Dijkstra算法这类采取遍历方法的算法带来了巨大的运算量。因此本研究编写的算法在每次选取下一寻径点时，不仅以到起始点的总“移动代价”之和最小为依据，而且加入了该点到终点的直线距离并给予适当权重，使得算法在寻找下一寻径点时带有一定的趋向于终点的趋势，可减少总遍历次数，提高运算效率。

通过以上方法，研究将设计场地中的空间条件转译为多因素影响下的三维寻径网络，并通过改写寻径算法使其可在该网络中进行三维寻径，从而构建了适应城市公共空间设计问题的三维路径探索算法模型（图1）。

2.2 算法模型回归建筑与城市设计问题

面对实际设计问题的需求，算法模型构建完成后，仍需根据相关建筑设计规范和建设可行性进行改进。在路径系统中，对于地面上的道路来说，只需要保证平面方向变化的合理性，但对于三维路径来说，有诸多建设成本和设计规范上的问题需要考虑。例如人行天桥，其坡度、坡长、休息平台、上下平台之间的高差等需要符合设计规范，避免出现直上直下、锯齿形上升下降或不合理的交错重叠。为此，算法模型中置入了重叠避让范围的参数设定，路径探索过程中在寻找下一寻径点时会避开不合理的节点，避免了类似三维路径上下层之间高度不够这类问题。同时程序界面也设定了参数可调节模式，使设计者可针对寻径结果通过参数调节去满足特定的设计要求（图2）。

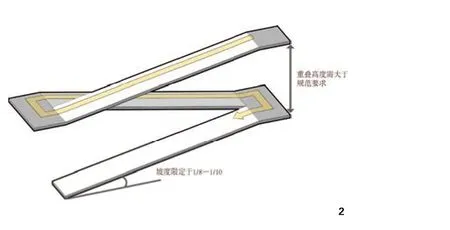
图2 算法模型寻径过程中的合理性判定条件

此外，在城市公共空间的实际设计中，场地内往往需要有多条路径交织成的一套路径系统。为此，如果需要探索多条路径，它们之间的关系也需要进行相互协调。例如过街天桥的位置及其底板距地面高度、天桥与天桥之间避免交叉重叠等。因此算法模型在每次寻径完成后，将基于现有路径系统对网络内的所有寻径点进行自查，将现有路径附近的寻径点的综合“移动代价”值调高，以保证后续探索到的其他路径不会与已有路径存在冲突。为确保算法模型在实际项目中的实用性，程序中加入了即时修改与即时反馈的环节。在路径探索结束后，设计者可依据结果对设计参数进行调整，快速获得修改之后的路径探索结果。本研究通过Java语言编程所建构的寻径算法模型的工作流程如图3所示3）。

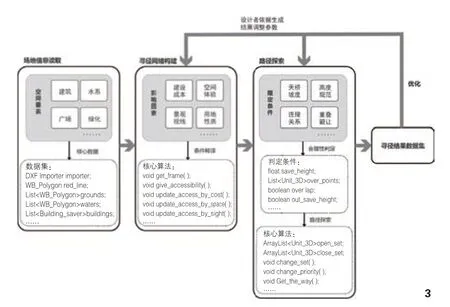
图3 本研究中寻径算法模型的工作流程

2.3 路径探索到规划设计的“数字链”流程

由算法模型得到的寻径结果是寻径网格模型内的一系列几何数据，提供的是路径规划方案的基本策略，尚未提供可用于实施的设计方案。本研究在寻径阶段结束后，通过编程方法打通数据从Java算法模型到Grasshopper建模软件的传递，以方便建筑师的进一步设计。首先在Grasshopper中建立应对寻径结果空间几何数据的运算器集合，桥面、扶手、结构柱与楼梯等细节均架构完成。随后利用iGeo作为数据导出的工具包，将Java算法模型中得到的三维路径数据导出为3dm模型。最后由Grasshopper建模工具读取模型中的路径数据，并进行数据控制下的路径系统的细节自动生成。

至此，本研究按照实际城市设计项目中路径系统设计的需求，完成了从读取场地信息并将其转化为数学模型并进行影响因素的分析与计算，到三维寻径算法完成路径寻径，再到将寻径数据结果传递到建模工具中完成方案深化设计的“数字链”工作流程（图4）。在这一流程中，场地分析与路径探索在算法模型中完成，方案深化则在Grasshopper中完成，每个环节之间均通过数据进行信息传递，提升了路径规划设计工作的方案科学性与工作效率的同时，又具有高效的反馈机制，可以在设计结果输出之前通过反复修改调节参数，快速获得修改后的方案直至满意。

图4 从场地信息读取到详细设计方案的“数字链”工作流程

3 数字链工作流程下的路径探索和设计实践

3.1 淮安井神盐化工厂周边城市空间更新设计

淮安井神盐化工厂周边城市空间更新设计项目位于江苏省淮安市，占地面积约52ha。规划中井神盐厂将搬离城市中心区，地块将从工业用地转变为城市公共绿地和商业用地组成的城市公共空间（图5）。项目区位紧邻淮安老城，位于大运河与里运河所夹江心洲地带，周边为密集的住宅区和教育设施，改造后将展示当地盐业和漕运业的变迁和未来发展。规划方案将原有的九个街区重新定位为工业遗址景观公园和核心商业区，设计保留了众多富有工业特征的盐厂设备与建筑，进行了建筑的改造与新建建筑布局设计（图6）。在这一空间中具有复合的功能空间、复杂的建筑形体和建筑风貌，其外围则有沿里运河和大运河的不同景观，因此一套满足人们观光、购物、运动、休闲的三维步行路径系统的设计是项目成败的关键。

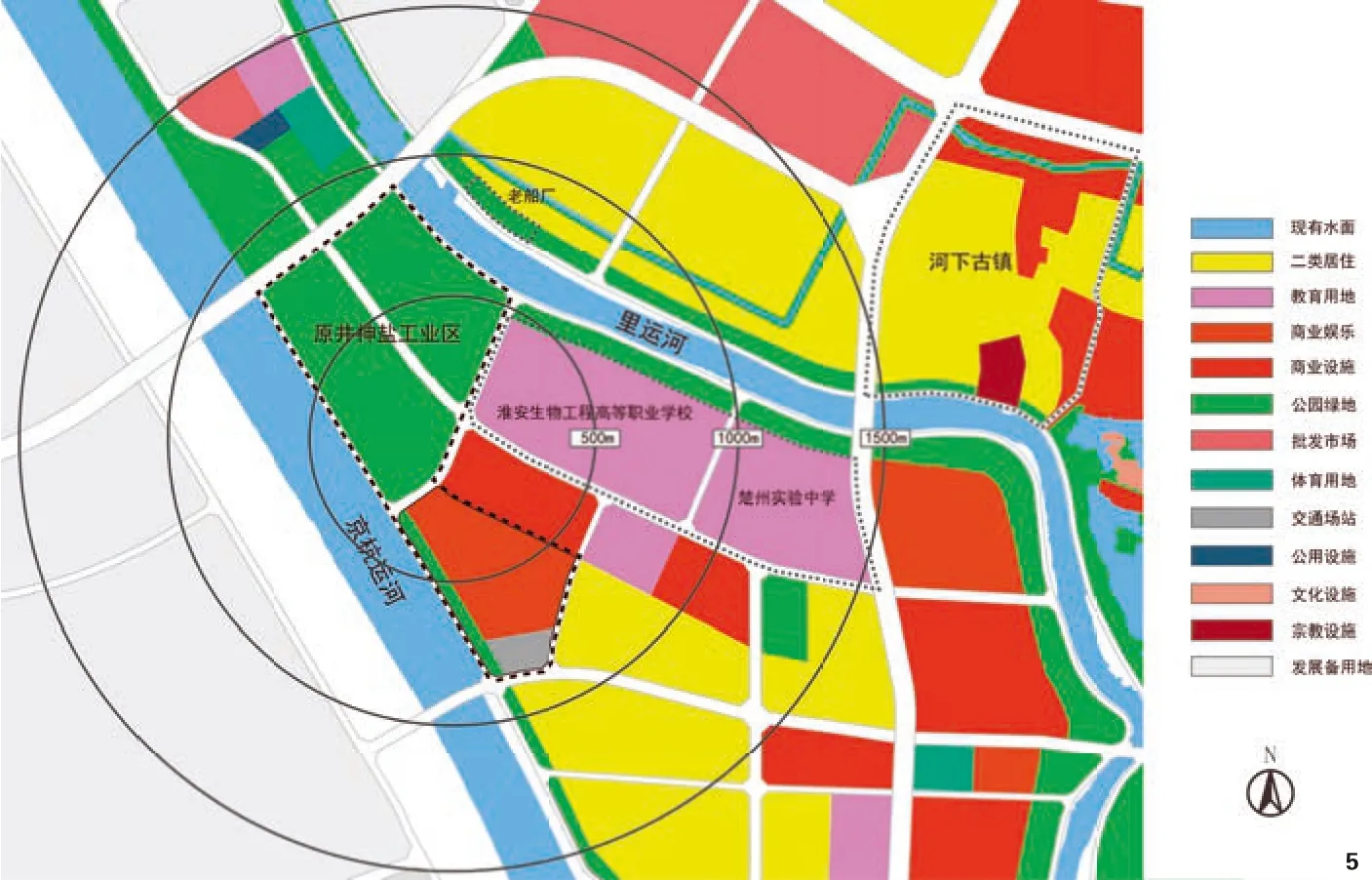
图5 井神盐工业区区位及周边用地总体规划

图6 更新改造后井神盐厂地块功能划分与建筑布局

3.2 “数字链”工作流程在实际问题中的应用

该项目中的三维巡游路径系统通过本研究构建的“数字链”工作流程完成初步规划设计，并在此支持下完成最终方案。

首先利用笔者开发的三维路径算法模型读取场地内的信息。由于场地范围较大，因此将场地内的9个地块独立作为分析对象，同时根据该方案所需的寻径结果精度与计算量的综合考虑，分别为9个地块建构了各寻径点在xyz三个方向上的间距为1m的三维寻径网络。随后设计师在算法模型的程序界面内手动选取了各地块内的核心功能节点与核心观景节点（图7），算法模型依据已经读取到的场地地形地貌信息以及各寻径点与上述功能、景观节点之间的关系，赋予三维寻径网络中每一个寻径点以综合“移动代价”值。

图7 场地范围内选取的功能节点与景观节点

之后由设计师在算法模型的程序界面内手动选取各地块内机动车需要通达的道路节点以及景观天桥需要经过的公共交通节点，这些节点将作为路径系统中的必经点。算法模型的程序界面可切换二维和三维两种模式，分别运行即可得到相应的节点之间地面车行道路和景观天桥路径（图8）。经过多次运行，可得到各个地块内基于空间体验、建设成本、景观视线、建设规范等条件综合价值判断后的路径系统（图9）。使得路径系统一方面能够通达地块中沿大运河和里运河的滨水景观，满足休闲和工业遗迹游览的功能；另一方面又能满足未来商业街区的人行购物和车辆交通的需求。

图8 算法模型的程序界面内的二维与三维寻径算法运行效果

图9 路径探索结果的整体与局部效果

最后，将算法模型得到的路径数据导入Grasshopper建模工具中，实现了道路与景观天桥面向实际建造的细节生成（图10）。设计师在此基础上进行了方案深化，不满意之处回退到寻径算法模型中进行了修改并重新快速获取路径探索结果，直至设计完成。

图10 场地中景观天桥的详细方案设计（局部）

3.3 路径探索结果的探讨

本次淮安井神盐厂大型城市公共空间的更新改造设计采用了“数字链”的工作流程，将三维寻径探索与方案设计实践进行了结合。从设计结果来看，本研究的工作方法在城市公共空间三维路径探索上达到了预想的目标。

但必须看到，本研究开发的工作流程依托经典寻径算法进行深度改写，其局限性在于算法运行过程基于特定的寻径网络，其结果不可避免地以像素化的方式呈现，因而路径探索结果不完全自由。部分路径弯道较多，路径系统在人为调整之前整体效果欠佳。在算法模型中，笔者虽然对公共空间的路径预设了部分合理性限定条件使其更接近实际问题的解决，但寻径算法本质上仍以起点与终点之间总“移动代价”趋于最小为寻径目标，获得的路径系统更多反映了移动代价的高低，无法控制整体路径布局的优美性，需要在下一步的方案设计中予以调节和细化。

4 总结与展望

城市公共空间中多元共存与交融的可能性越来越被城市和社会学者所重视[19]，也就需要城市设计的手段能满足多元使用群体产生的日益复杂的需求。在城市设计中由于路径规划问题的量化和计算依据较为明确，且设计目标有合适的算法支撑，适合运用程序算法建立能反映多因素影响的设计工具。本研究以此为研究目标并在完成基本数据提取和建立程序算法的基础上，将算法的寻径结果与既有数字化建模工具之间进行数据衔接，拓展出从场地分析到路径探索到方案深化的一体化工作流程。该设计方法解决了三维路径设计中的复杂计算问题，整合了多种影响因素，使城市公共空间的路径规划设计不再仅仅依靠主观判断；同时“数字链”设计流程的应用提升了城市公共空间设计的合理性，推动城市公共空间向更通达、更便捷、更安全、更宜居的方向发展。

数字技术的快速发展为城市设计的技术创新提供了多种可能[20]。本研究以路径规划为切入点，在城市设计的实际过程中证实了数字技术贯穿分析到设计全流程的可行性和有效性。该技术思路同样可以应用在城市设计工作中的其他复杂问题中，通过对设计问题进行深入细致的研判和梳理，将设计问题合理转为程序算法，以数据链接解析、判断和生成设计的各个阶段，从而实现形态到数据的逆向建模过程与数据到形态的正向设计过程的连接，形成数据驱动的设计与分析的良性互动，能够为城市设计提供更多更好的解决方案[21]。这也是本研究所揭示的数字技术在城市设计中进行深度应用的另一层技术意义。

致谢：衷心感谢东南大学建筑学院李飚教授，博士研究生蔡陈翼、王笑、李金泽对本文的贡献。

图、表来源

图5：来自淮安市自然资源与规划局；其余图片、表均由作者绘制。

注释

1）对于表中提到的四种寻径算法，其时间复杂度（以O表示）与寻径网络的总点数（以N表示）及总边数（以M表示）相关。Floyd算法运行时会找到所有顶点对之间的最短路径的长度，其时间复杂度为O(N3)，因此在解决寻径点较多的网络中的问题时会产生较大的运算量。Bellman-Ford算法相对Floyd算法效率有所提高，其时间复杂度为O(NM)。SPFA算法是Bellman-Ford算法的队列优化算法，其效率不稳定，在面对同一问题时最不理想的情况下与朴素Bellman-Ford算法时间复杂度相同。因此为避免最坏情况出现，在面对点数较多但无负权的网络时应使用堆优化后时间复杂度为O((M+N)logN)的Dijkstra算法。

2）将Dijkstra算法与最佳优先搜索结合以提高运行效率即A*算法的策略。A*算法本质上是为Dijkstra算法提升运行效率的一种拓展，其算法原理与Dijkstra算法类似。

3）三维路径探索的算法模型源代码均为笔者通过Java语言编写。由于篇幅原因，此处仅列出中的部分核心数据集与关键方法。