量化分析方法在康泽恩城市形态学中的运用探索*——以广州传统街区为例

引言

康泽恩学派是西方城市形态学的主要流派之一，近年来被介绍到中国，显示出在研究中国城市发展和历史保护[1]等方面有着切实的适用性[2]。该学派的核心目标是形态区域（morphological region）的划分，是平面类型、建筑类型、土地或建筑利用三个要素综合叠加整合形成的[1，3-5]。但是，多年以来，这种方法以感性成分居多，量化分析不足，使形态区域的客观合理性受到了一定程度的影响。

当代信息技术的发展和学科的交叉融合，使得像组构学这样的形态研究方法快速发展，统计学和计算机新技术也被应用至城市研究当中[6]。康泽恩城市形态学也应当积极利用这些新的技术手段来提高研究水平和实践的应用效率。因此本研究旨在结合空间句法、类型指标量化、城市大数据，应用统计学方法，在GIS平台上进行整合，对康泽恩学派的形态区域划定方法进行量化改良。

1 经典形态学和近年的量化探索在单一要素和整合方法上仍然存在不足

康泽恩1960年在安尼克镇（Anlwick）的平面格局分析当中就有意识量化形态，以平面类型的单一要素为主，对地块、建筑的尺寸以及数量、占比等进行了一定的量化研究，但是由于时代局限性，人工效率和计算工具的限制使其停留在较小范围的描述性统计分析，对街道和平面形状则是抽象地描述；在对多个量化指标进行综合判断、划分单元时，缺少有效量化整合的工具，只能以归纳的方式得出平面类型单元和形态区域[3]。

时至今日，康泽恩学派的单一要素分析融入了能更精细量化形态的方法。

改进集中于平面类型，如黄慧明[7]、郑剑艺[8]等以分形维度量化描述街道系统和街区的形态，但是分形维度仅能计算、表达已有区域的形态特征，不能对整体区域进行形态的细分。空间句法却能一定程度上弥补这一缺点，它计算所得的组构值能在研究范围内不同等级和结构的道路之间形成有效区分，这已经得到了普遍认知，因此也能在UNA、Morpho和Form Syntax等多要素整合叠加工具中占一席之地[6]；部分康泽恩学派研究者也已经尝试融合空间句法，验证了组构值可帮助划分平面类型单元[9，10]，但令人意外的是，尽管较早的研究已经将空间句法的改良进行了总结[11]，他们在模型构建和组构值计算上依然采用了局限性较大的旧方法，因此仍有必要进行比较和辨析。

经过量化的形态指标却只作为比较与归纳整合的参考，数据的客观性未被充分利用，缺少量化整合的方法。参考其他多要素整合的研究，Form Syntax尝试回应了平面、建筑和功能三要素，建立量化体系并通过分项到综合评级的方式进行了整合[6，12]；Gil等人[13]和赵雨薇[14]的研究则从建筑类型学的角度采用了数据挖掘的方法对各指标进行了综合判断和分区。但是以上两种研究均以街区为基本研究尺度，无法达成微观尺度下的形态区域细分；而建筑尺度的量化整合研究[15]则对形态层面的要素考虑不周，使得成果离散，未形成有机的形态区域。

2 康泽恩学派视角下的形态量化模型构建

以地块为基本尺度，分别提取形态区域要素的量化指标，再使用数据挖掘的方法进行整合、优化，如此能结合经典学派与前沿研究的优点，是量化划分形态区域的基本思路，本文基于该思路构建了以下形态量化研究模型。

2.1 形态要素量化

首先是分别提取形态区域三要素的代表性指标，利用GIS平台计算并赋予形态分析单元——产权地块，统一分析对象，构成城市形态数据库。

2.1.1 平面类型

被分作街道系统、产权地块和建筑基底三个层级进行考虑[16]，在实际分析过程中，这三个层级本身及其相互之间的关系都是量化分析的难点。

关于街道系统，不同于经典学派将道路形态归纳为“方格网状”、“鱼骨状”等抽象类别，空间句法能以近似于视觉结构[17]的方式，客观描述道路或者开放空间的形态并数值化；地块序列（产权地块的组织关系）也在路网模型足够细致的条件下，体现在计算结果中，达到区分不同街道的层级结构、空间逻辑和地块序列的目的。

产权地块和建筑基底本身的量化取决于二者的平面几何性质，如形状、尺寸和方向。而针对地块与基底之间的关系，目前的技术并没有很好的量化方法，一般采用建筑密度等占有率指标来概括。

2.1.2 建筑类型

康泽恩学派对于建筑类型的考虑包括建筑的结构、材料和层数等，而地方性的建筑类型划分常常不止于此。建筑的历史风貌、平面尺寸、功能或是特色构造，都会成为建筑类型划分依据，实际上透支了其他形态要素，平面类型和功能混入其中，造成了一定的混淆。因此在建筑类型这一要素的指标提取时，应当甄别并提取独立的建筑类型指标，如结构、层数等。

2.1.3 土地利用或建筑功能

这一要素实际上已经有了较为成熟的分类规则，可优化之处在于大范围的数据采集效率。而网络开放数据（以POI为代表）的逐步发展，提供了快速途径。

2.2 量化指标整合

其次是多维度指标（变量）的量化整合，SPSS平台的K均值聚类分析1）提供了较为合适的解决办法。各种不同纲量的指标经过Z-score标准化2）后得以计算个案相互间的距离，划分出基于数据本身特征的类别，经由GIS的可视化和对K值（即聚类数）的多次调整，完成对形态区域的划分和优化。而建筑结构、建筑历史风貌以及土地利用等分类变量3），则可以通过分级、有序化后再进行聚类（图1）。无法有序化的变量则可拆分为虚拟变量4）来代替类别属性。

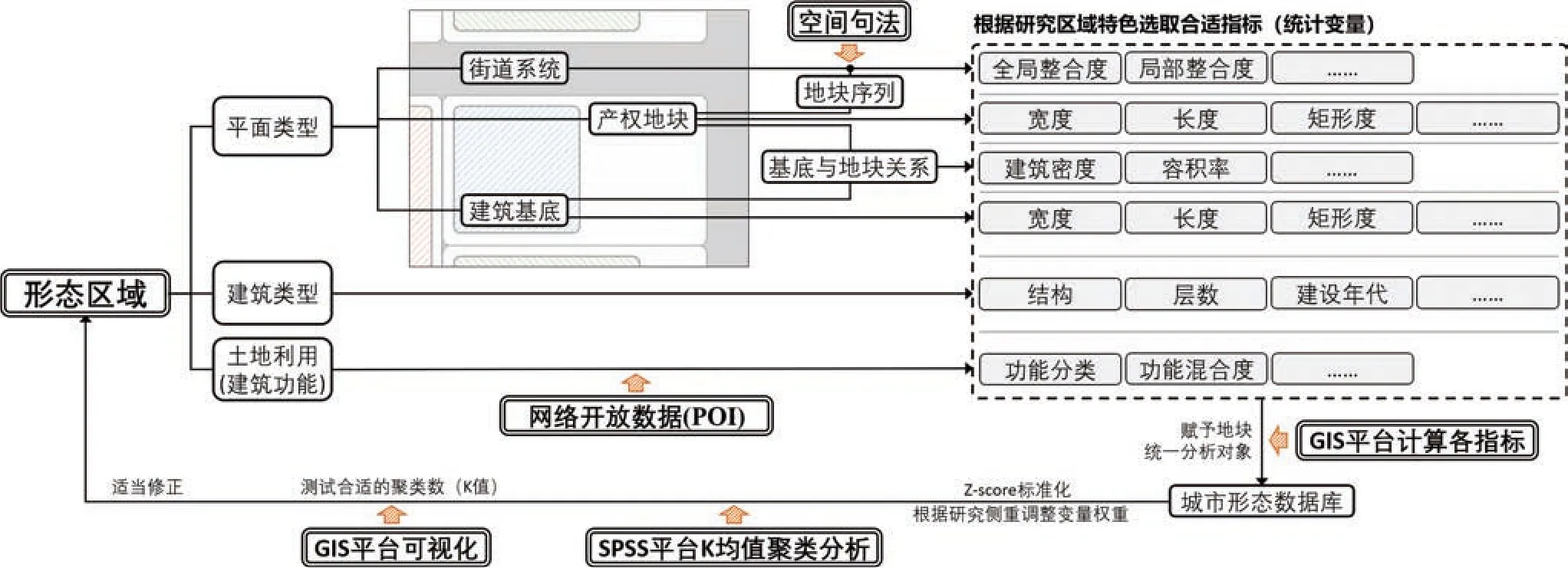
图1 康泽恩城市形态学量化研究模型示意图

3 以广州传统街区为例的指标体系构建及其计算方法

特定的研究区域有各自合适的指标体系，应当结合地方特色和现状数据，选择在特定区域内能明显区分不同类型、形态的指标。由于K均值聚类方法的限制，也应尽可能选择有序且连续的变量。下文以广州传统街区为例，选取和辨析量化指标。特别地，由于中国的城市形态研究缺少准确、大范围的产权地块数据，而且广州的传统建筑有建筑基底与产权地块几乎重合的特点，在本例中以建筑作为基本分析单元。

3.1 平面类型指标

3.1.1 街道系统、地块序列——空间句法

空间句法的理论和计算方法在不断发展过程中不断被改良，而目前被康泽恩学派研究者应用的路网模型和计算方法都还存在一定的局限性。

（1）路网模型构建：轴线法与线段法

宋明星等人的研究[10]中对道路模型的构建采用了轴线法，而线段法作为轴线法的改良方法，相较于轴线法有着更为客观、准确的路网绘制原则，结合测量半径，能有效区分类似的路网布局，也接近于传统的道路交通分析[11]，更符合康泽恩学派对道路系统关注的重点。

（2）计算加权方式：米制距离和转弯角度

城市分区源于不同尺度城市空间的互相影响，有必要测度全局和局部两个尺度的组构值并进行综合考虑[18]。角度加权法已被证明能更加有效捕捉城市空间布局细微差别[11]，从全局角度来说已基本达成共识。但从局部来说，Li xiaoxi等人使用米制整合度5）（MMD）以回应局部空间的米制特征[9]，而MMD在Hillier等人的研究中被指出仍有诸多缺陷[19]，不适于直接量化空间。笔者在广州传统街区也进行了测试，表明大测算半径下的MMD无法进行有效细分，而小测算半径作出的区分也仅能表达路网密度的分异，地块序列并不明确（图 2）。事实上，线段模型的测量半径已经涵盖对米制特征考量，在全局和局部尺度都使用角度加权的线段模型就能较好地区分不同的街道结构和等级。

图2 米制整合度未能良好辨别平面类型上的分异（示例范围为广州南华东地区），组构值经由后文方法赋值建筑

（3）具体组构值选型：选择度与整合度

空间句法计算所得组构值较为多样化，用于描述街道空间层级的多为整合度与选择度[9，10，12]。笔者从全局尺度针对整合度和选择度（均经过后文方法赋值建筑）进行了分类效果对比（图 3上、中），可见整合度和选择度都可以表达可达性、区分不同的街道段的等级，但是整合度的数据分布更为均匀，利于聚类。而选择度，即使经过标准化，它的计算逻辑决定了无论道路等级如何，尽端路的选择度均为“0”，不能进一步相互区分（图 3下）。

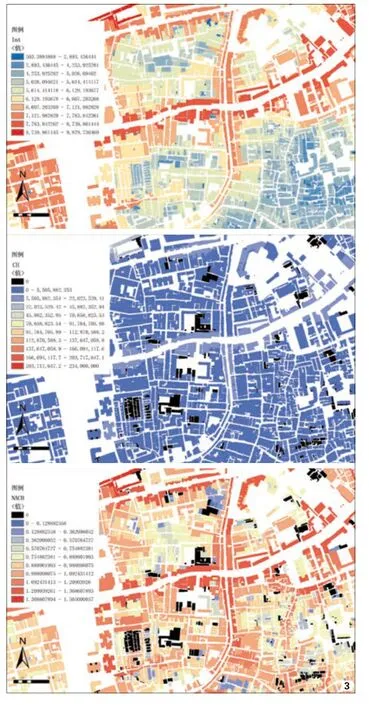
图3 同福西路地区建筑全局组构值分类图，上为整合度，中为选择度，下为标准化的选择度，黑色区域组构值为0，组构值经由后文方法赋值建筑

因此本研究采用线段法构建路网模型，在全局和局部尺度都选择角度加权计算的整合度，其中局部尺度测算半径的选择，根据文献[20]对广州北京路历史街区的研究，鉴于其地域和尺度的相似性，取其研究结论——400m，对应步行者自然活动的最大距离，该半径既能与全局尺度分析形成区别，也能满足广州传统街区尺度的形态识别（图 4）。

图4 状元坊传统街区的全局角度整合度和400m测算半径局部整合度（经过下文方法赋值建筑）

路网模型的精度和广度都会影响组构值的准确性，现有的康泽恩学派相关的量化探索都存在路网精度上的不足之处[9，10，12]，这也是平面类型划分未能细分到街区内部的原因之一。本研究以2010年广州1∶2000的地形图为基础结合局部实地调研勘误、更新的方式绘制了整个历史城区范围的细致路网，并根据“30分钟测试”经验法则[21]73-74扩展到了如图 5（左）所示的范围。可见路网模型囊括大街小巷（图 5（右）），为街道系统和地块序列层面的平面类型细分打下了基础。

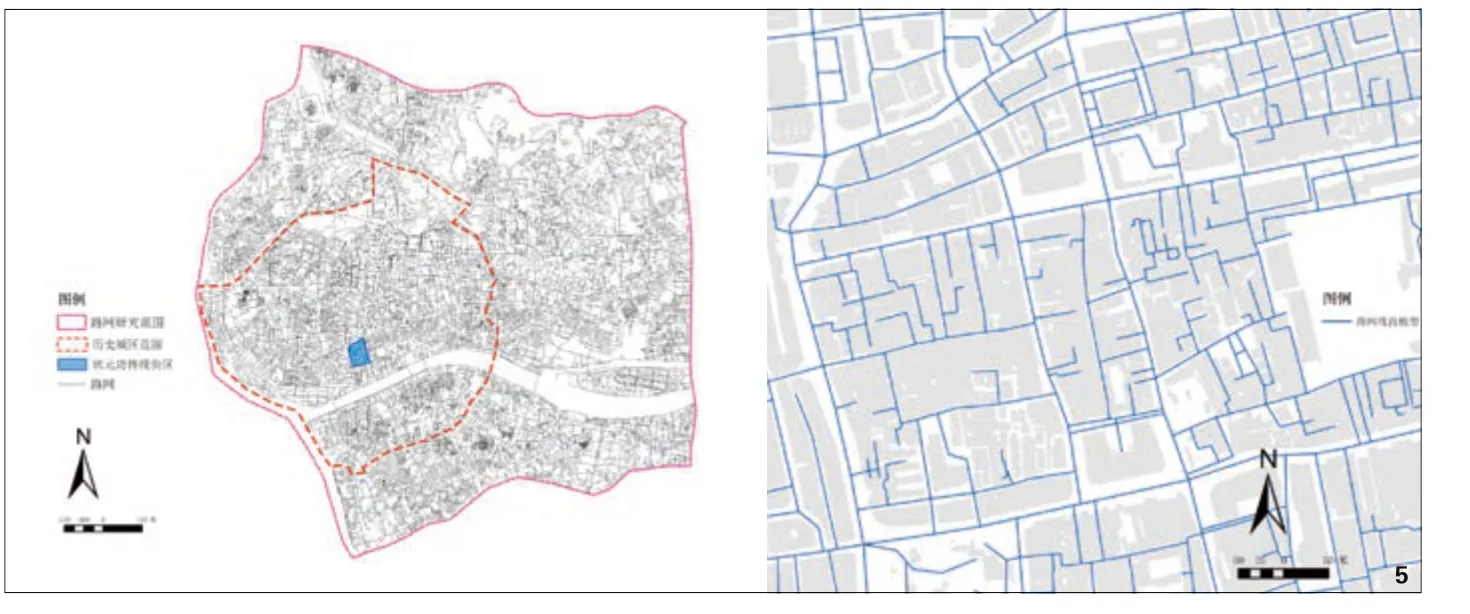
图5 路网模型范围、历史城区范围、状元坊范围（左）；路网线段模型细节（右）

经过DepthmapX软件的计算，结果以线要素形式呈现，需要统一分析对象，赋予建筑。如果以直线距离赋予，会造成部分可达性较差但是距离主要道路直线距离短的建筑赋值不合理（图 6、图 7上）。本研究提供一种方法使路网的组构值更为合理地赋予建筑要素：在GIS中为开敞空间、灰空间6）、实体建筑依序赋予不同的成本值，将组构值以成本分配的方式划分给整个研究区域，设置距离衰减，最后在建筑内取最大值。

该方法能弥补空间句法在线段绘制时未顾及到的细节，并加强对空间局部米制特征的描述。而且，取组构最大值，相较于平均值，能将地块出入口的模式体现在组构值当中，利于地块序列的识别（图 6、图 7中、下）。因为多边临街的建筑，往往在可达性高的街道上设置主出入口。

图6 组构值赋予建筑示意图

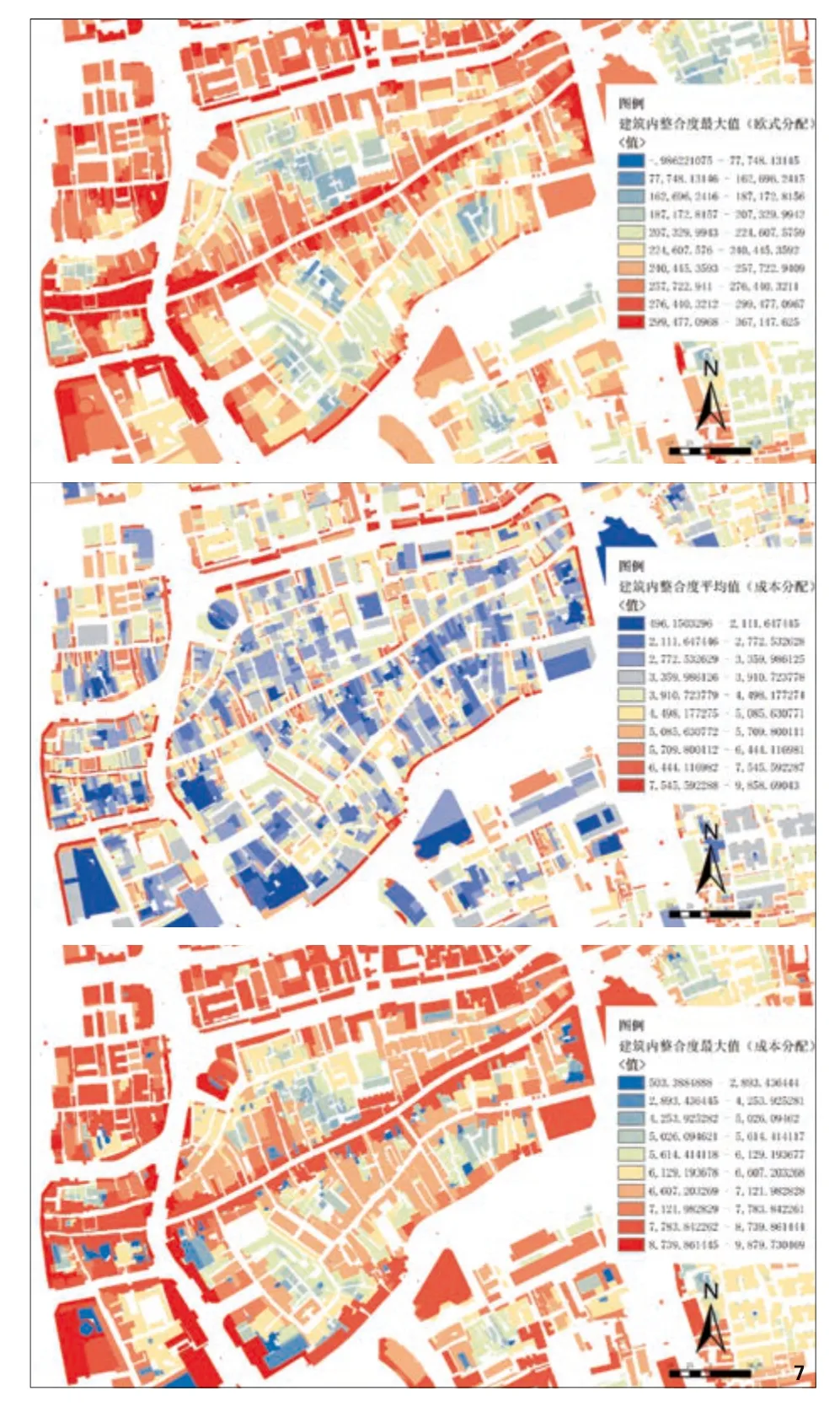
图7 直线距离赋值（上）赋值后于建筑内取平均值（中）赋值后于建筑内取最大值（下）

3.1.2 产权地块和建筑基底

广州传统街区有高密度、低强度、均质化的特点[22]，建筑能被以群组的方式划入“亚街区（图 8）”，用于计算建筑密度和容积率（图 9），概括建筑基底与产权地块的关系，是产权地块资料缺失条件下的近似替代方法。同样，由于地块与基底几乎重合，基底的几何属性也能近似表达地块形态，选用朝向7）、基底最小外接矩形8）长度和宽度、基于面积的矩形度9）和基于周长的矩形度10）等。

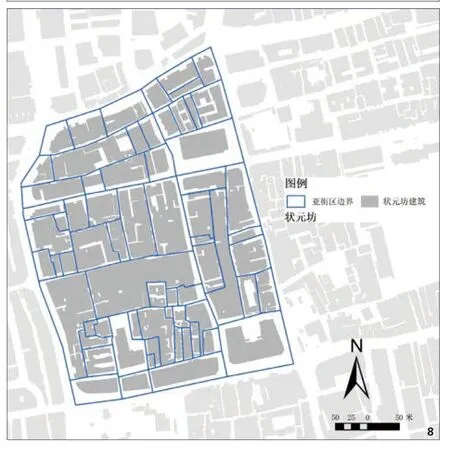
图8 状元坊的“亚街区”划定

图9 状元坊基于“亚街区”的建筑密度（左）和容积率（右）

3.2 建筑类型指标

广州传统街区的建筑以竹筒型大进深的建筑为主[22]，其惯常的建筑类型根据建筑的开间、进深和功能等被划分为“竹筒屋”、“明字屋”、“西关大屋”等[23]，而这种分类方式与康泽恩城市形态学的另外两个要素产生了交叉，在量化指标的提取时，应当先回避平面类型和功能相关的指标，形成分类独立的指标体系，以免聚类时被重复计算。

本研究选用如建筑层数、结构的常规类型指标以及建筑年代（来源于文献[9]）、风貌等级（来源于文献[23]）这样能反映建筑的历史分层、体现康泽恩城市形态学中对形态时期的考虑的指标，并加入“是否骑楼”这一地方特色建筑构造指标，帮助划分区分明显的形态区域。

3.3 土地利用或建筑功能指标

土地利用和建筑功能的数据一般有两种来源：一种是规划勘测部门提供或实地调研得到的土地利用图；另一种是基于网络开放数据（如高德地图POI）处理得到。大尺度下，网络开放的新数据比传统的规划用地数据能更精准地反映城市空间的使用情况，且分类更细，但是在微观尺度应用时也存在一定的误差[21]100。由于传统街巷内部的功能数据缺失、POI的坐标也无法精确配准到建筑上，与实际功能产生了较大偏差（图 10），因而在数据准确度有限的广州传统街区，功能数据仍应通过规划勘测部门或实地调研获取。

图10 状元坊街区的高德地图POI点密度（左）、实际土地利用（右）

4 状元坊传统街区的实证研究和分析示例

状元坊街区位于广州历史城区范围内，是广州知名商业内街，其所在区域有多种传统商业空间、居住空间的历史遗存，建筑类型和城市形态多样[24]，特别是广州传统民居的原型——竹筒屋，在其中有着各种变体[25]。也已有多项学术研究和规划编研对该区域进行了深入细致的城市形态和建筑类型研究[24-29]。因此，状元坊街区是非常适合形态量化研究的方法验证、对比的典型案例。

如前文所述构建指标体系如表 1并可视化为图 11，形成了城市形态数据库。

图11 状元坊量化指标可视化总览

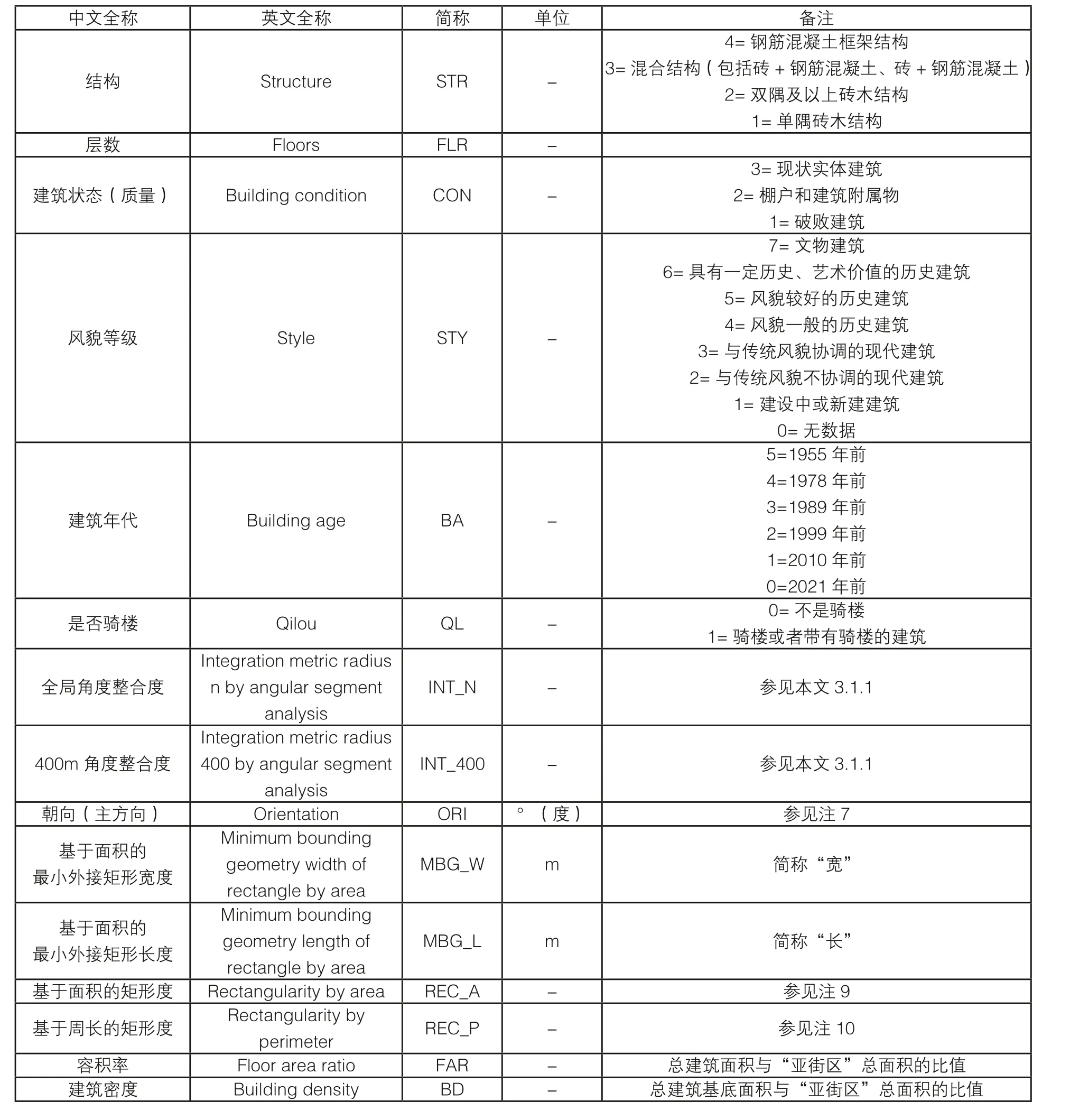
表1 量化指标（变量）总览表

4.1 平面类型与建筑类型的聚类

针对功能相对单一的研究区域，形态区域的划分可相对忽略对功能的考量[4]，而且整合度本身与商业的分布呈现较高的相关性[30]，已经能一定程度上代表功能对形态的影响。因此本研究先对平面类型与建筑类型指标进行一次整合。

在SPSS软件中对指标进行了K均值聚类分析，经过多次试验，当K=12时能呈现较好的可视化分类结果（图 12），排除异常的个案后聚类数与研究者在状元坊划分的建筑类型数接近[27]，足够支持与功能指标进一步叠合为形态区域，分析报告如下（原始数据均已作Z-score标准化处理）：

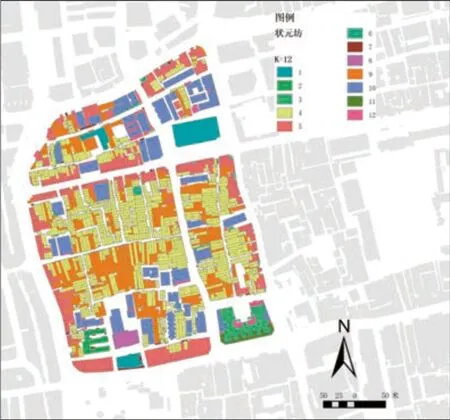
图12 K=12时平面类型和建筑类型指标聚类分析图

本次聚类分析在第25次迭代时，所有聚类中心的最大绝对坐标变动为0.001以下，因此算法已经实现了收敛。同时表 2 ANOVA显示各变量的显著性（Sig.）显示除建筑性质（CON）以外的其他变量均在聚类分析中有贡献11）。而建筑性质在本实证研究范围内几乎都为“3”（实体建筑），无法产生区分，因而在本次聚类中未产生贡献，该变量可忽视，本次聚类结果仍可保留。

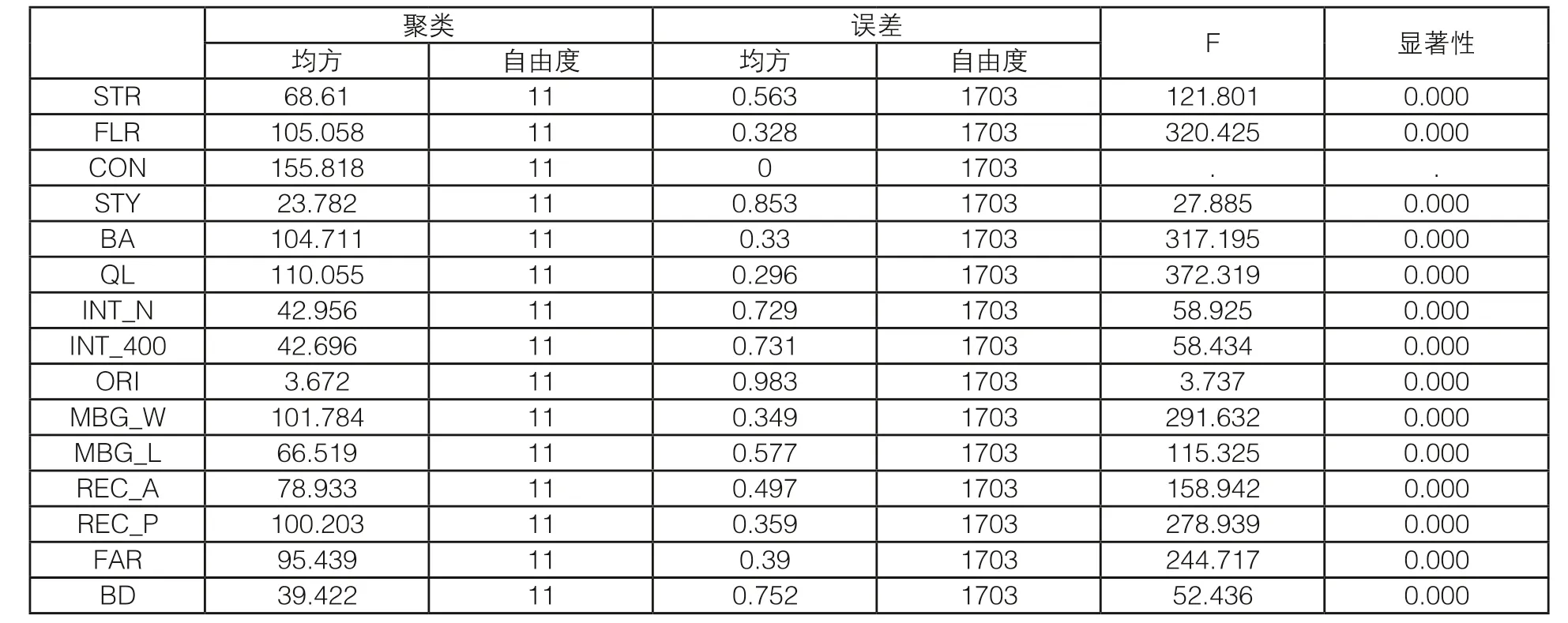
表2 ANOVA

表 3反映的是各最终聚类中心的各变量均值，表中加粗标识了每个聚类中明显区别于其他指标的值。

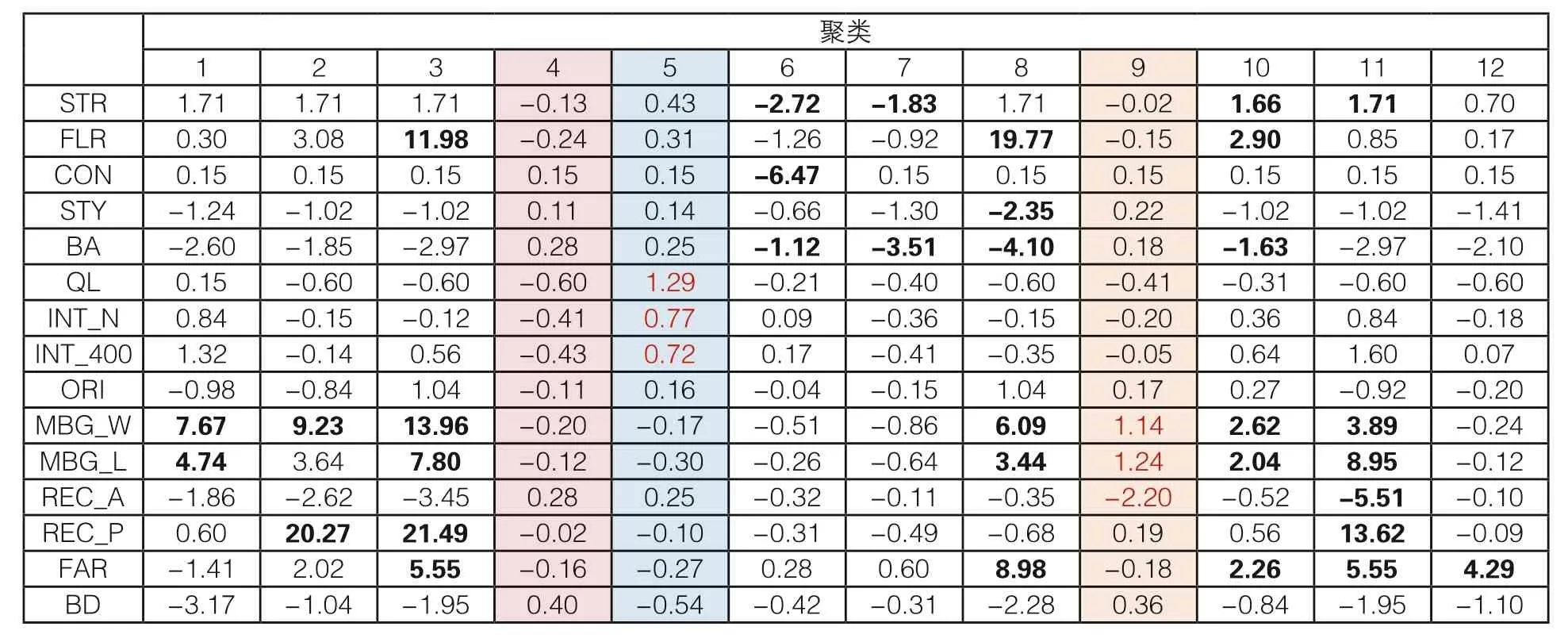
表3 最终聚类中心

从聚类观察指标，可以判断聚类的主要特征，对形态区域进行归纳。聚类3的建筑层数、长和宽和矩形度的数值显著，结合可判断该聚类为基底不规则的中高层建筑。同理，聚类10则是长宽稍大、建筑年代较新的低层建筑。而聚类4的各项指标均接近于0，是整个研究区域内数量最多，形态最普遍的常规竹筒屋。

从指标观察聚类，可以区分聚类在各指标上分异，帮助理解形态区域的划分原因。聚类4和5各个变量的均值比较接近，但是在“是否骑楼”和整合度上出现明显区别。实际上，骑楼街屋从竹筒屋演进而来，在基底和建筑结构等方面的确相近，区别在是否有柱廊和是否临街（可达性）；而聚类4和9，分别在长、宽和基于面积的矩形度上有明显区别，这表明这两个聚类建筑的开间进深以及基底规整度不一样，可以区分多开间的传统民居和形状不规则的特殊竹筒屋。

4.2 叠合土地利用/建筑功能

在完成平面类型和建筑类型相关指标的聚类分析后，将建筑功能也加入聚类分析。由于篇幅限制，在此省略聚类的详细报告，仅对可视化结果进行展示：

从图 13～15 可以看出由于缺少历史演进的视角和对地块序列的细致探究，本方法对形态区域的亚区细分还有提升空间。但是通过图 14与图 15的对比能明显看出该方法的划分结果仅需经过连接和填补，第一等级的区域划分就能与经典方法几乎一致。总的来说，仅基于现状数据能做到图 14的划分结果，作为快速的结果或是深入研究的基础都是可靠的。

图13 左为K=12时的形态区域，右为K=30时的形态区域

图14 K=12作为形态大区和亚区的划定依据，K=30作为最低层级单元划定依据的叠合图

图15 研究者通过经典形态学方法划定的形态区域图

结论与讨论

本研究方法分别基于形态区域要素构建了量化指标体系，结合了空间句法对平面类型的量化、GIS技术对图形指标的计算和可视化、数据挖掘方法的整合分析，并对城市大数据于土地或建筑利用的识别进行了尝试。以广州状元坊为案例，方法达成了与经典康泽恩学派研究方法近似的结果，证明了方法在微观尺度的可行性，并为分析结果的归纳提供了思路，能为城市形态研究的继续深入提供数据支撑和可个性化调整的研究路径，也能为规划编制提供更客观的形态区域化成果。

由于网络开放数据在微观尺度上的失准，在功能的量化时效果不佳，因此在功能多样的区域，需要获取更准确的数据。但是在某些功能较为单一的研究区域，如住区，即使不考虑功能要素，仅以平面类型和建筑类型作整合，该方法也能达到不错的分区效果[4]（图 12）。

本研究的量化方法基于现状数据，缺乏对历史演进的细究，构建的方法在中低层级的形态区域划分上与经典方法出现了差异。同时，K值的选择较为主观，需依靠多次试验和经验判断，有所局限；但是K值也可以根据研究的深度和侧重进行对应调整，较为灵活。例如，形态区域各要素有着稳定性的差别，对形态的影响力不同[31]，那么在聚类之前，可以根据研究区域的主要特征，为变量赋予权重；或是研究侧重于某一要素，也可以提高对应的变量权重。

受限于研究领域，在指标的选择、整合的方法上还有不少提升的空间。随着信息技术的不断发展，人工智能也应在城市形态研究中发挥更重要的作用。已经有学者应用机器学习进行图像识别来综合评价街道空间品质[32]。同理，可以期待在城市形态的量化过程中，将建筑基底与产权地块的关系、建筑风貌等判断难度大且不同研究者的评判标准难以统一的指标经过由专家训练的人工智能统一辨识、量化。

致谢：感谢黄慧明、姚圣在研究资料上的支持；感谢邓可欣、何思亮、罗思仪在研究资料的调研和整理上的支持；感谢孙华伟、孙永生、李晔、杨舒雅、赵雨薇在研究方法上的指导和讨论；感谢李晨阳在空间句法的理论与应用上的讨论与建议；感谢邱亭谕、廖韬在数据挖掘和图形特征识别上的指导和建议。

图、表来源

图 10（右）、15：引自参考文献[27]；其余图、表均由作者绘制。

注释

1）K均值聚类法，或 K-means聚类法，可以将各自包含大量数据的个案快速分为 K 个类别，同时尽可能地最小化每个类别的均值与该类别中所有对象之间的差异性，有计算快速、结果便于理解的优点，且能根据研究需求调整分类数量和权重。

2）Z-score标准化，也叫标准差标准化，这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，均值为0，标准差为1。

3）分类变量（Categorical Variable）是说明事物类别的一个名称，值没有数量的特征，仅区分类别。

4）虚拟变量（Dummy Variables）又称虚设变量、名义变量或哑变量，通常取值为0或1，可用于拆分并数值化分类变量的各个类别。

5）米制整合度，平均米制深度（MMD）的倒数，能有效捕捉有相似组构特征的街道段，并能形成马赛克分区（patchwork pattern）现象，区域数值上类似，具有相近的色彩（参见参考文献[33]），体现了街坊的大小和形状在不同的城市功能空间之间的变化（参见参考文献[34]）。

6）灰空间，指建筑与其外部环境之间的过渡空间，比如骑楼、甬道等，也包含周边的绿地和半开放场所。

7）朝向，建筑基底以正北方向作为起点，顺时针旋转的角度。

8）最小外接矩形，在ARCGIS软件中由最小边界几何工具（minimum bounding geometry）计算得到，计算规则为基于面积（by area）。

9）基于面积的矩形度（rectangularity），建筑基底面积与其最小外接矩形面积的比值，可以衡量基底与规整矩形的近似度。值域为(0,1]。

10）基于周长的矩形度，建筑基底周长与其最小外接矩形周长的比值，可以衡量基底建筑图形近似于矩形或正交扭曲后的矩形的程度，如“L”形。

11）统计分析中一般认为显著性（Sig.）值在0.05以下的变量对聚类有显著贡献，聚类结果可以保留。