基于时间序列模型的上证A股指数实证分析

宋雅晴，康晴晴，刘 兮

(合肥师范学院 数学与统计学院，合肥 230601)

自沪深两市交易所1990年开市之后，规模日益扩大，上市公司数量与日俱增，A股市场机制不断健全与完善，成为重要的资本市场。2019年科创板规则正式落地，为创新驱动打开了空间，股市发展进入了一个新阶段。股市中的某些规律性隐匿于市场内部，对股价历史轨迹形态的描绘与演绎，可为未来价格趋势预测提供重要线索，因而构建精准的模型兼具理论与实际意义。鉴于此，丰富完善股票指数内容，创新股价指数预测方法，能够使投资者、政府决策者、企业决策者准确地把握股市波动的规律性，在瞬息万变的股市中做出明智选择。

1 文献综述

20世纪80年代起，国外学者将时间序列分析研究视野转向了多变量、异方差、非线性场合，有效补充了ARIMA模型的不足。Black(1976)发现股价波动的杠杆效应，即利空消息与利好消息对波动的影响是非对称的[1]；Bollerslev(1986)提出了GARCH模型，刻画了金融市场风险的变化过程[2]；Nelson(1991)等提出了TARCH和EGARCH两个非对称模型[3]。近年来，鉴于中国股市的特殊性，国内学者提出了多种股市走势分析方法。刘红梅(2008)对鞍钢股份建立了ARIMA模型，进行了短期分析[4]；吴朝阳(2010)利用改进的灰色模型与ARMA模型进行股指预测[5]；郭海樱(2010)基于ARCH模型实证分析了上证A股指数收益率的波动情况[6]；符一平(2015)等利用ARCH簇模型对上证综指进行实证研究，得出上证综指具有明显的尖峰厚尾性、波动聚簇性、信息不对称性[7]。钟立新(2020)等基于GARCH-MIDAS模型分析了政策因素对股市波动长期成分的影响[8]。基于此，对2017-2021年的上证A股指数进行时间序列分析，筛选出最优模型，为加强我国股市的合理性提出一些建议。

2 模型简介

2.1 Box-Jenkins模型——ARIMA模型

Box-Jenkins方法利用外推机制描述时间序列，能达到最小方差意义下的最优预测。ARIMA(p,d,q)模型结构如下：

(1)

其中，p表示自回归阶数，d表示差分阶数，q表示移动平均过程的阶数，{et}为零均值白噪声序列，∇d=(1-B)d,Φ(B)=1-φ1B-…-φPBP是p阶自回归系数多项式，Θ(B)=1-θ1B-…-θqBq是q阶移动平均系数多项式。

2.2 GARCH簇模型

Bollerslov基于ARCH理论，提出GARCH模型，增加了对异方差函数p阶自相关性的考虑，可拟合具有长期记忆性的异方差函数；为提高预测精度，可采用GARCH的衍生模型。具体模型有以下几种形式：

①GARCH模型：

(2)

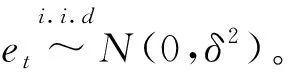
②AR-GARCH模型：

(3)

③EGARCH模型：

(4)

④GARCH-M模型：

(5)

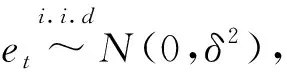
2.3 水平——波动综合模型

鉴于全面性考虑，采用ARIMA模型与GARCH簇模型分别提取序列水平与波动信息，既可对序列未来水平进行预测，又可绘制波动置信区间图，完成对序列更完整的认识。

3 实证分析

3.1 选取数据

为了确保科学性和实效性，以2017年3月20日-2021年3月19日的上证A股指数收盘数据为样本数据，预测时间为2021年3月22日-26日；通过与真实数据对比，评价预测精度，选出最佳模型。

3.2 数据预处理

第一，原始序列平稳性检验。为了判断数据的平稳性，首先进行单位根检验如表1所示，ADF检验统计量为-2.11，P=0.24>0.05，即具有非平稳性。因此，为了消减序列波动，对原序列作一阶差分运算。

表1 上证A股ADF检验结果表Tab.1 Shanghai A shares ADF test results

第二，差分序列性质考察。对差分序列进行ADF检验，结果表明差分序列具有平稳性；由图1、图2可知，偏自相关系数具有明显拖尾性；同时通过对差分序列进行白噪声检验，得到P值小于0.05，即为非白噪声序列。因此，在下一步建模中，应分别提取水平和波动信息。

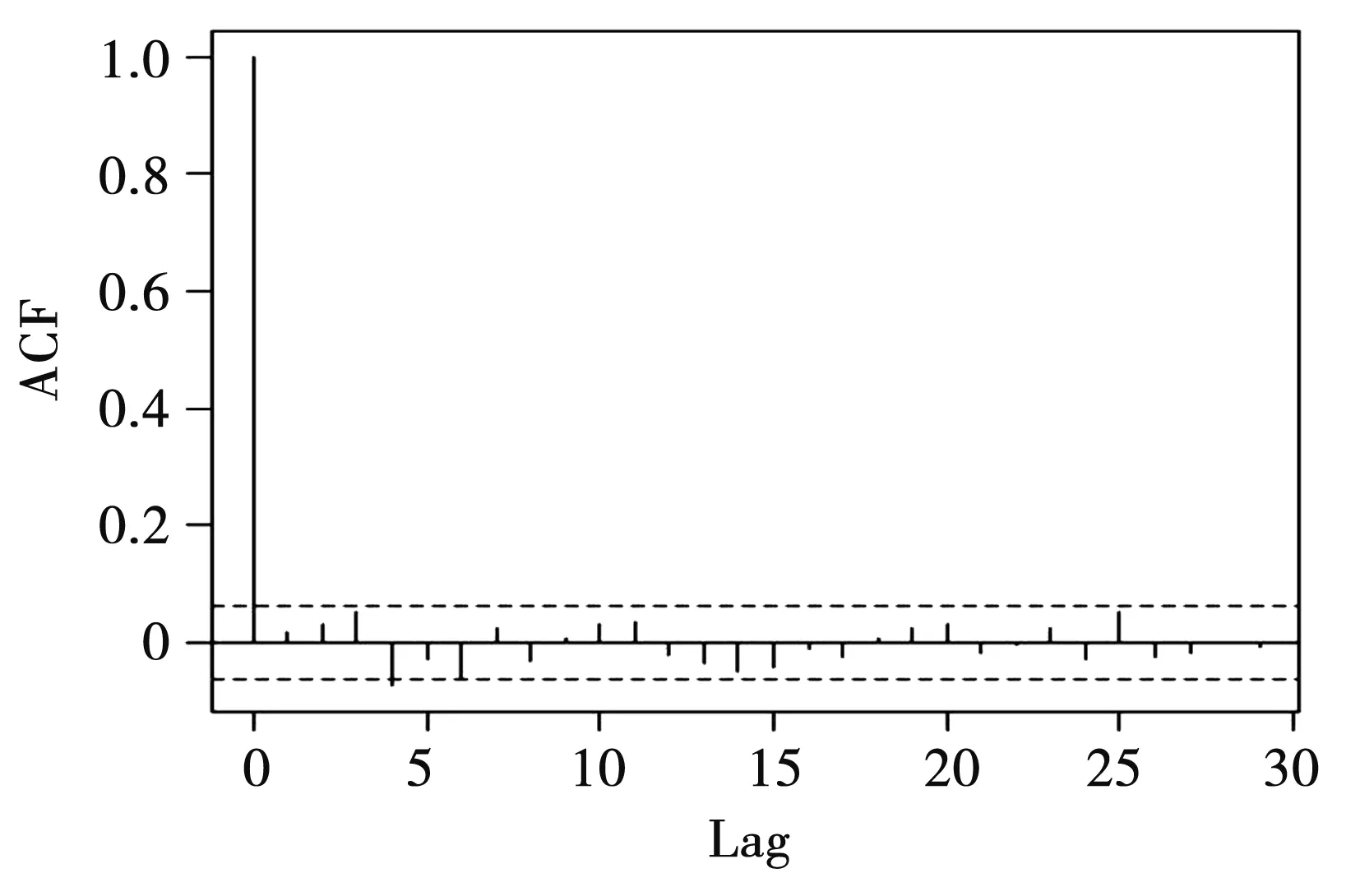
图1 差分序列自相关图Fig.1 Autocorrelation diagram of difference sequence

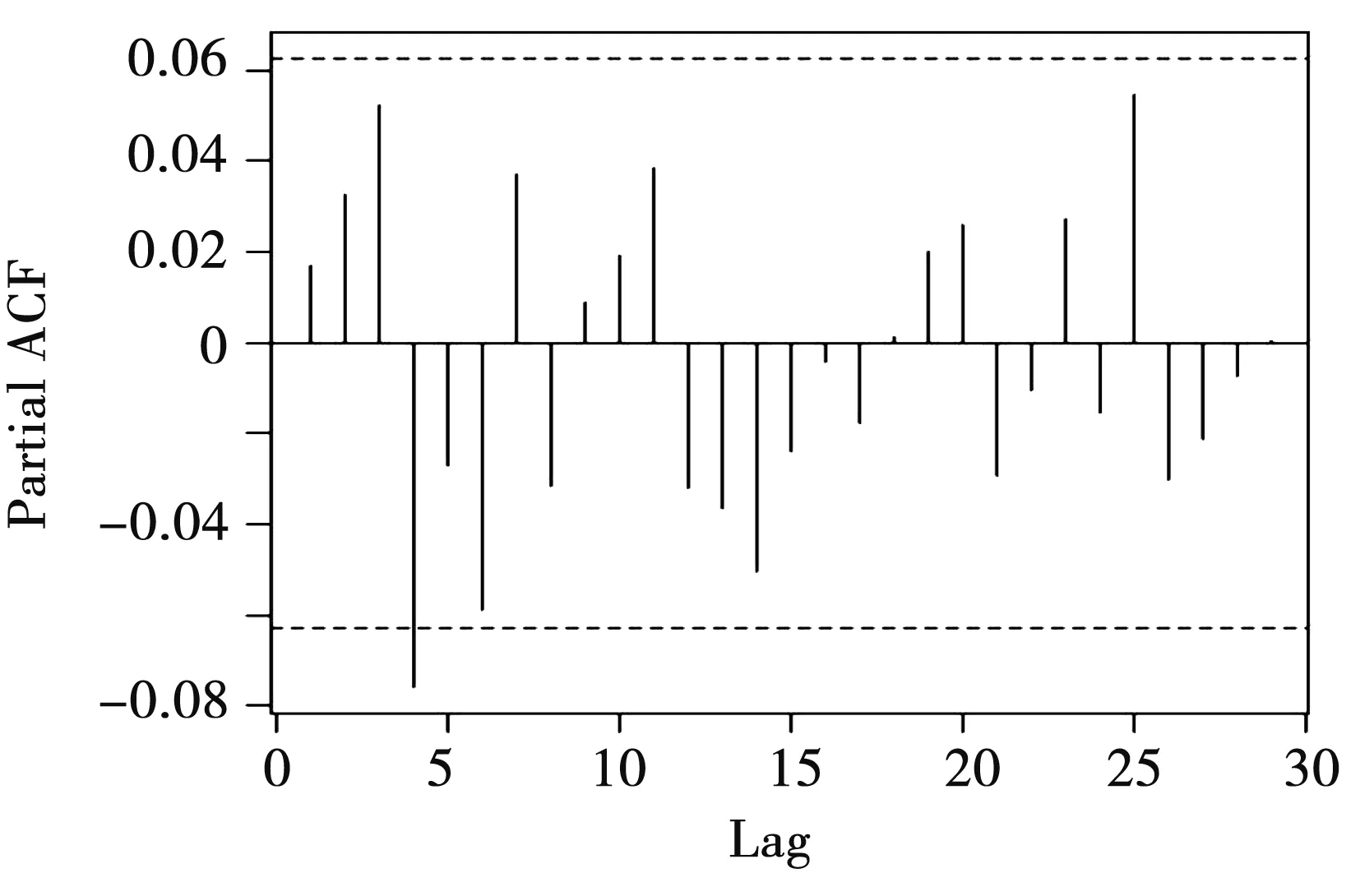
图2 差分序列偏自相关图Fig.2 Partial autocorrelation diagram of difference sequence

3.3 建模分析

第一，水平信息提取。通过对比分析与模型识辩，建立最终模型为ARMA(2，1，2)，表达式如下：

xt=0.375 1xt-1-0.892 2xt-2+et+0.374 3et-1-0.932 7et-2

(1)

残差白噪声检验显示，P=0.66>0.05，即残差序列具有随机性，且各参数通过检验，模型显著有效。运用ARIMA(2，1，2)模型，估计出2021年3月22日-26日共5个交易日的收盘价如表2所示。

表2 上证A股收盘价预测表Tab.2 Closing price forecast of Shanghai A shares

比较ARIMA(2，1，2)模型的预测值与真实值，发现相对误差均很小，且真实值基本都落在95%预测区间之内，说明该模型精度较高、预测效果良好，能够用来预测上证A股指数的走势。

第二，波动信息提取。为了检验模型的残差是否具有ARCH效应，进行异方差检验，根据LM检验，可知χ2=31.199，P=0.002<0.05，即残差序列呈现出异方差、长期相关的特征。拟合GARCH模型，经过调试得到EARCH(1，1)模型中参数对应的P<0.05，说明模型拟合效果较好。为了进一步检验序列的“杠杆效应”，拟合非对称的EGARCH模型，模型中参数均显著，存在杠杆性。通过对比分析可知，EGARCH(1，1)拟合效果最优。如表3所示。

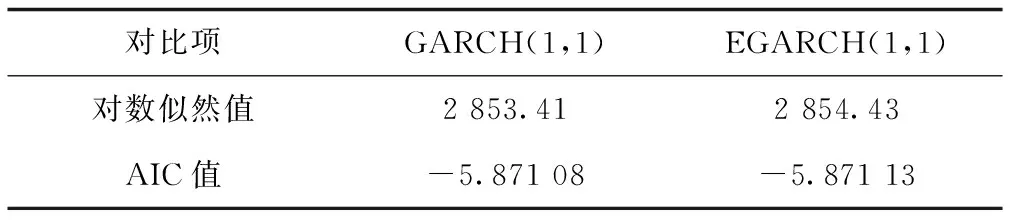
表3 GARCH(1，1)与EGARCH(1，1)模型检验比较表Tab.3 Comparison of GARCH(1，1) and EGARCH(1，1) model

EGARCH模型为：

(2)

在各种lag值下，F统计量对应的P<0.05，模型无ARCH效应，拟合效果良好。根据以上分析，可以得出最优模型——ARIMA-EGARCH模型如下：

(3)

4 结论与建议

以上证A股指数为对象，建立了ARIMA模型和GARCH簇模型，评价分析预测结果，最终筛选出最优模型。得出结论：上证A股指数的波动具有持续性、非平稳性的特点，差分序列具有平稳性；ARMA(2，1，2)模型残差序列存在异方差性，具有ARCH效应，EGARCH(1，1)模型拟合效果最优。为了加强我国股市的效用性与合理性，规避股市风险，提出以下建议：国家应完善法律法规，规范股市运营手段，真正实现依法治“股”；政府应建立健全股市机制，转变职能地位间接调控股市；企业应合理优化资源配置，加强自身创新能力与竞争力；投资者应加强对股市的洞察力，提高自身防御风险的能力。