零彗差自由点条件下的失调光学系统波像差特性分析*
吴 伟,于乃辉,罗自荣,白向娟,尚建忠
(1. 国防科技大学 智能科学学院, 湖南 长沙 410073; 2. 国防科技大学 前沿交叉学科学院, 湖南 长沙 410073;3. 中国人民解放军31636部队, 云南 昆明 650300)
光学系统的成像质量不仅受到设计过程中残余像差的影响,还受到加工误差、装调误差、温变、振动等因素的综合影响。波像差作为光学检测过程中评价系统成像质量的一个重要指标,其特性直接反映了光学系统的工作性能[1]。在光学系统的装调过程中,通过分析失调系统的波像差特性,可为评估实际的装调状态提供有效指导,众多学者针对该领域进行了研究[2-10]。Hopkins等[2]建立了旋转对称光学系统的经典像差理论,揭开了光学系统波像差特性分析的帷幕;文献[3]回顾了矢量像差理论的发现历程,指出对于失调的光学系统,并没有增加新的波像差,只是系统的像差场特性发生了改变;Thompson[4]在其博士论文中对这一特性进行了详细的介绍,基于矢量像差理论分析了偏心和倾斜两种失调误差引入的像差场特性:三阶彗差和三阶像散分别在全视场范围内存在一个和两个视场节点(零点),且节点的位置与失调状态直接相关。因此,对于失调的光学系统,轴上彗差和像散一般不为零,所以在光学系统的传统装调过程中,经常以轴上视场的三阶彗差是否为零作为系统是否完善装调的依据。但Mcleod[5]发现两反式光学系统中存在一个特殊的点,当次镜绕该点转动时,不引入额外的三阶彗差,揭示了传统装调评估方法的弊端,并指出还需检测轴外视场的像差才能准确评估系统的装配性能。随后,Schmid等[6]以Ritchey-Chrétien两反式光学系统(简称RC系统)为研究对象,基于矢量像差理论定性分析了该现象,指出该系统像散的一个节点会位于轴上视场附近。同期,Thompson[7-8]将博士论文的研究成果重新总结并发表到期刊上,基于矢量像差理论分别分析了两反系统和三反系统在失调情况下的像差场特性,为失调状态计算提供了理论依据。庞志海等[9-10]也基于矢量像差理论对两反和三反系统失调情况下的像差场特性进行了研究,指出由于零彗差自由点的存在,需要测量多个视场的波像差来确定系统的装调状态。徐少雄等[11]通过分析同轴三反系统失调后的彗差变化特性,提出了一种通过次镜偏心补偿三镜失调引入像差的方法。徐春梅等[12]则通过分析透镜横向失调对像差的影响,提出了一种考虑像差特性影响的失调校正方法。综上可知,对失调光学系统的像差特性分析是光学系统设计和装调过程中的重要环节,目前对常见失调的研究已经较为全面,但是对满足零彗差自由点这一特殊失调状态的研究还存在不足,大多停留在定性研究,缺乏理论解析模型的指导;此外,大多数研究虽然指出了要根据多视场的波像差才能判断系统是否完善装调,但是基于多视场的像差评估法无疑会增加人力物力,降低系统的装调效率,亟待更有效的评估方法。
因此,本文基于矢量像差理论,深入分析满足零彗差自由点这一特殊失调状态下光学系统的波像差特性,建立像散双节点位置的解析计算公式,量化分析该特殊失调对双节点位置的影响,并在此基础上寻求一种仅通过轴上视场的波像差评估系统是否完善装调的方法。由于失调主要引入三阶波像差,并且在装调过程中也主要根据三阶像散和三阶彗差评估系统的装调状态,因此本文主要针对这两部分波像差展开研究。
1 理论基础
1.1 矢量像差理论
20世纪80年代以前,主要采用几何分析法[13]分析装配误差对失调光学系统波像差特性的影响,直到文献[3]通过引入矢量乘法的概念,将Hopkins[2]建立的旋转轴对称光学系统波像差的标量形式改成矢量形式,从而建立起矢量像差理论,揭开了像差解析分析方法的序幕。随后,Thompson[4,6-8]通过总结前人的工作,发现对于失调的光学系统,并没有增加新的像差类型,而是系统的像差场特性发生了改变,在视场矢量H中应该引入额外的偏心向量σj,从而得到失调光学系统波像差的矢量形式,如式(1)所示,并将矢量像差理论推到新的高度,随后众多学者开始采用该理论进行失调计算和波像差特性分析。

(1)


图1 光瞳矢量、视场矢量和视场偏心矢量示意Fig.1 Conventions for the pupil vector, field vector and field decenter vector
对于失调的光学系统,其三阶彗差和三阶像散的矢量形式[14]分别如式(2)和式(3)所示。
(2)
(3)
其中
(4)
(5)
(6)
(7)
(8)
(9)
因此,对于三阶彗差和三阶像散未校正的系统,即W131≠0,W222≠0,可推导其各自节点位置的计算公式,即
(10)
(11)
其中,A131,a222和b222与失调误差直接相关,因此节点位置也受到失调误差的影响。综上,针对三阶彗差和三阶像散是否被校正的光学系统,总结其在存在失调和不存在失调时的全视场像差场特性,如表1所示。

表1 光学系统的全视场像差场特性
根据表1可以得出以下四点规律:
1)对于三阶彗差未校正的系统,三阶彗差与视场呈线性关系,在全视场范围内只有1个视场节点,并且节点的位置与失调状态有关,不存在失调时,节点位于中心视场。
2)对于三阶彗差校正的系统,三阶彗差在全视场范围内为恒定常数,不存在失调时,该常数为零。
3)对于三阶像散未校正的系统,三阶像散与视场成二次关系,且最多只有2个节点。存在失调时,具有双节点特性,节点位置与失调状态有关,不存在失调时,双节点位置重合,则只体现出1个节点,位于中心视场。
4)对于三阶像散校正的系统,存在失调状态时,三阶像散与视场呈线性关系,存在一个与失调状态相关的节点,不存在失调时,三阶像散在全视场范围内恒为零。
1.2 零彗差自由点
根据式(2)可以看出,对于失调的光学系统,存在一类特殊的失调状态,即当失调误差使得A131=0时,由失调引入的三阶彗差恒等于零,此时失调系统的三阶彗差场特性与不存在失调时的情况一致。
对于光阑位于主镜的两反式光学系统,以主镜作为基准,对次镜进行装调,只有次镜存在失调误差。通过求解式(5)即可得到这类特殊的失调状态应满足的条件,即
(12)
根据文献[14]中偏心矢量的计算公式,将其代入式(12),进而可以求解得到次镜的失调误差应满足如下公式:
(13)
其中
(14)
式中,XDE和YDE分别表示次镜沿X、Y轴的偏心误差,ADE和BDE分别表示次镜沿X、Y轴的倾斜误差,d1表示主次镜之间的间隔,rsm表示次镜的曲率半径。
对于确定的两反式光学系统,可知比例系数m是唯一确定的,因此,次镜偏心和倾斜的失调状态组合可以转化为次镜绕某点的转动,即对两反式光学系统,存在一个固定的点,当次镜绕该点转动时,其失调状态引入的偏心矢量始终满足式(12),则该失调引入的三阶彗差恒等于零,该固定点即为零彗差自由点,如图2所示,该点与次镜顶点之间的距离即为m,如式(14)所示。

图2 零彗差自由点示意Fig.2 Conventions for the coma-free pivot point
综上可知,对于两反式光学系统,存在一类特殊的失调状态,当失调满足绕零彗差自由点转动的条件时,即使失调没有校正,轴上视场的三阶彗差仍然为零。因此,传统装调过程中仅靠轴上视场彗差是否为零来判断系统是否完善装调是不充分的。
此外,对于多反式光学系统,当每个镜片的失调状态都满足式(15)时,可知即使系统还存在失调,也不会引入三阶彗差,每个镜片都存在着一个零彗差自由点。
(15)
两反式光学系统是目前天文观测、空间遥感的重要结构形式,为该类光学系统装调过程中提供有效指导,以解决实际装调过程中由于零彗差自由点的存在导致单视场像差难以评估系统完善装调状态的问题,下面对该类特殊失调状态下的波像差特性展开深入分析。
2 零彗差自由点对系统波像差特性的影响分析
2.1 三阶彗差特性分析
当存在的失调使镜片满足绕零彗差自由点转动时,根据式(2)、式(4)、式(5)和式(12),推导得到系统三阶彗差的计算公式为:
(16)
此时,失调系统的三阶彗差场特性与完善装调时完全一样,且彗差在设计之初是否因被校正而呈现全视场内恒定为零或者与视场呈线性关系的特性,因此无法仅根据三阶彗差的状态评估系统是否存在失调误差。
2.2 三阶像散特性分析
根据矢量乘法法则[7],联立式(6)~(9),可以得到:
(17)

(18)
进而根据式(3)、式(9)和式(11)推导得到该特殊失调情况下三阶像散双节点位置的解析计算公式为:
(19)
不同两反系统的设计参数不同,计算得到的t值也不同,根据式(18)可以定量分析三阶像散的双节点位置,下面结合具体的光学系统进行分析。
3 实际案例分析
3.1 RC系统的波像差特性分析
本节以RC系统[14]为例,分析基于零彗差自由点失调情况下的像差场特性。该系统的光学设计参数如表2所示,系统口径为3 m,F数为20,全视场为±0.12°,计算主、次镜三阶彗差和三阶像散的系数如表3所示。从表3可以看出,该系统在设计阶段校正了三阶彗差,其主、次镜的三阶彗差系数之和为零,由表1可知,该系统完善装调情况下三阶彗差在全视场范围内恒为零。

表2 RC系统的设计参数
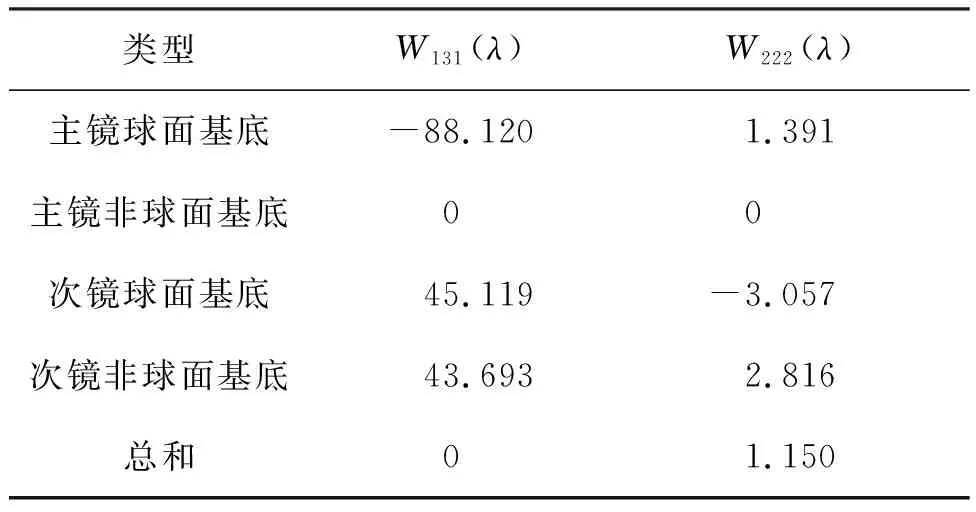
表3 RC系统的波像差系数
根据表3和式(18)计算得到t=0.001 75,将其代入式(19)计算得到该特殊失调情况下三阶像散的双节点位置(0,2a222)。
显然,一个节点位于零点,另一个节点的位置则与具体的失调状态有关。下面根据零彗差自由点条件设置三组不同的失调状态组合(如表4所示),对其波像差进行仿真分析。

表4 引入的三组失调状态组合情况
基于CODE V对该RC系统进行建模,并通过像差全视场分析功能(full-field-display, FFD)分析表4中三组失调状态下的三阶像差特性,如图3所示。
根据图3,对于该RC系统,分析其在存在满足零彗差自由点这一特殊失调状态时的像差场特性,可以得到以下规律:
1)与2.1小节的理论分析一致,该特殊失调情况下三阶彗差的全视场分布与完善装调时的情况完全一样,如图3(a)、图3(c)、图3(e)所示。
2)对于三阶像散的双节点特性,当完善装调时,双节点重合,位于中心视场,如图3(b)所示;而存在失调时,一个节点仍然位于中心视场,另外一个节点偏离中心视场,且其位置与失调状态直接相关,如图3(d)、图3(f)所示。
3)对三阶像散,存在失调时,虽然中心视场的像差依然为零,但是可以看出不同失调状态的像散在全视场的分布特性是不同的,这也是为什么部分文献[5,8-10]中提到,由于零彗差自由点的存在,仅仅通过轴上视场评估系统完善装调是不充分的,还需要检测轴外或边缘视场的像差。然而在实际像差检测过程中,实现轴外多视场需要耗费较大的成本和较长的时间,因此,亟待一种高效的装调状态评估方法。

(a) 彗差(失调状态1)(a) Coma (misalignment case 1)
3.2 两反系统完善装调的轴上视场像差评估法
评估光学系统是否完善装调的本质在于获取系统当前的装配误差,而对于两反系统,在光学检测过程中,三阶彗差和三阶像散由四项泽尼克系数表征,正好可以计算出四个侧向失调误差(XDE/YDE/ADE/BDE),但由于零彗差自由点的存在,导致在该类误差求解的过程中,存在满足特殊失调状态的奇点,因此部分学者通过获取额外视场下的波像差来增加方程约束,从而提高失调状态的计算精度。
随着柔性高精密夹持机构[16]的出现,使得光学系统的装调朝着自动化、智能化的方向发展。在大型望远镜的建造过程中,为了补偿重力、振动、温度、冲击等因素引入的形变对系统像质的影响,也设计有精密六维调整机构,以通过调整次镜位姿进行补偿校正,如VST望远镜[17]、TMT望远镜[18]、HST望远镜[19]等。
因此,在两反系统的装调过程中,通过高精度装调机构实现镜片位姿的精确调整是切实可行的,也是未来智能制造的发展趋势。基于此,本文提出一种仅基于轴上视场像差的装配性能评估方法,具体的操作步骤为:当两反系统轴上视场的三阶彗差和三阶像散都为零时,借助精密装调机构对失调参数(一般选择偏心误差)引入特定的失调量,通过评价指标(merit index, EI,如式(20)所示)计算引入失调前后轴上视场的像差变化,从而评估系统的失调状态,如图4所示。
(20)


图4 基于轴上视场像差的装调状态评估法Fig.4 Method of assembly condition assessment based on the aberrations in axial FOV
还是以RC系统为例,当轴上视场的三阶彗差和三阶像散都为零时,先不管当前失调状态的具体值,假设当前的失调误差为表4中三组状态中的一种,直接对次镜再引入Y向1 mm的偏心误差,通过CODE V仿真三组状态引入失调前后轴上视场的像差结果,并计算评价指标EI值,如表5所示。

表5 引入定量失调前后的波像差及评价指标
由表5可以看出,虽然三组失调状态的初始像差都为零,但是在引入1 mmY向偏心误差后,三组状态的像散都发生了变化,并且存在明显的差异,从失调状态1到状态3,原始误差越大,预置一定失调后引入的像散也越大,这是因为失调误差对三阶像散的影响存在耦合性[20]。根据表5中的EI值可知,只有状态1是完善装调的,因此,在轴上三阶彗差和三阶像散为零的情况下,通过引入确定的失调量,并根据引入失调前后的像差数值变化来评估初始的失调状态是切实可行的。
4 结论
基于矢量像差理论,总结了失调光学系统中三阶彗差和三阶像散的全视场波像差特性:三阶彗差与视场呈线性关系,在全视场范围内只有1个节点,三阶像散与视场成二次关系,在全视场范围内存在2个节点;并在此基础上重点对一类特殊的失调情况——满足零彗差自由点条件的失调状态进行了深入研究,建立了该特殊失调下像散双节点位置的解析计算公式。研究表明,该特殊失调不引入三阶彗差,并且会使像散的一个节点位于中心视场附近,揭示了装调过程中不能仅基于轴上视场三阶彗差为零作为系统完善装调的标志,并基于波像差特性的分析结果,提出了一种基于轴上视场引入定量失调前后的波像差变化来评估系统完善装调的方法。以RC系统为研究对象,通过仿真验证了所建立解析计算公式和完善装调评估方法的可行性。本文对于理解反射式光学系统在失调状态下(特别是满足零彗差自由点条件)的波像差特性和提高反射式光学系统的装调效率具有重要意义。现有试验条件无法实现失调量的精确定量调节,但是文中的理论分析和仿真结果已经验证了所提方法的有效性,下一步将基于现有的一套76 mm口径的同轴两反系统,研制一套面向精密装配的试验平台,从试验上探究该方法的可行性,并研究基于单视场波像差的装配误差计算方法。

