分布式异构集群中节点优先级调优算法*
胡亚红,邱圆圆,毛家发
(浙江工业大学 计算机科学与技术学院(软件学院), 浙江 杭州 310023)
Spark是专为大数据处理而设计的快速通用的计算引擎,但是它原生的资源调度策略建立在集群同构的基础之上[1-3]。随着硬件的更迭及高性能部件的引入,集群节点的性能逐渐变得各不相同,集群的异构性日渐凸显[4-5]。Liang等[6]研究发现,同构环境下的资源分配策略不能考虑负载的特性,从而导致原生的Spark调度策略在异构环境中不能充分发挥集群的性能。
目前学者们针对如何提升Spark和Hadoop异构集群性能进行了许多研究[7-9]。郑晓薇等[10]指出Hadoop集群采用原生的任务调度方法,负载不均衡问题常有出现,因此提出了基于节点能力的Hadoop集群自适应任务调度方法,即根据节点的历史和当前负载状态,以节点性能、任务特征等作为节点任务量调度分配的依据,自动地调整任务量。Gunasekaran等[11]考虑Hadoop异构集群特性,提出使用时间约束启动模型策略以减少任务的等待和启动时间。Xu等[12]研究了异构的Hadoop集群下集群节点的动态变化和负载情况,提出采用动态调整的调度算法以实现集群性能优化。虽然都是大数据处理框架,但是Spark和Hadoop在性能研究方面存在着较大差异,Hadoop集群中所采用方法不完全适用于Spark集群。因此,对于提升异构Spark集群性能的研究非常重要[13-14]。
樊森[15]考虑异构Spark集群下的Task调度问题,提出以最小化最大完工时间为优化目标,针对具有DAG偏序关系的Job和Stage以及同一Stage中并行Task之间的问题特点和特征建立数学模型,优化了Task调度算法。基于Spark on Yarn模式,Wang等[16]提出了考虑作业截止日期和值密度的硬实时调度算法以提升集群性能。Kuzmanovska等[17]则基于多个数据处理框架,提出用Mesos反馈控制器动态调整框架权重以进行任务调度。杨志伟等[18]指出Spark集群默认的任务调度在异构环境中未考虑节点能力差异,提出了异构Spark集群下自适应任务调度策略。该算法监测节点的负载及资源利用率,利用监测得到的参数动态地调整节点的任务分配权重。徐家俊等[19]指出现有的调度策略对于异构Spark集群效果不佳,提出了综合考虑任务复杂度、节点性能及节点资源使用情况等因素的分层调度策略。基于集群异构导致计算资源不均衡、Spark现有的任务调度未考虑集群的异构性以及节点资源的利用情况,胡亚红等[20]提出了基于节点优先级的Spark动态自适应调度算法。
神经网络在特征提取和建模方面具有独特优势[21-24]。Zhang等[25]将BP神经网络(back propagation neural network)应用到云计算环境中以进行实时调度,实验证明了算法的有效性。文献[26-27]分别在Spark环境中使用神经网络完成了电压偏差预测和交通网络流量预测,均取得了很好的效果。越来越多的研究将Spark和深度学习连接在一起,譬如Moritz等针对现有流行的批处理计算框架不支持分布式深度学习系统和密集型工作负载的问题,提出了专用于训练深度网络的Spark框架SparkNet[28]。SparkNet能够大幅提高深度网络的训练效率。
现有研究工作在进行集群资源分配和任务调度时多是基于节点的性能优先级进行。为了得到合理有效的节点优先级,通常需要建立集群节点优先级评价指标体系,并确定各评价指标的权重。指标的权重对于计算节点优先级起着至关重要的作用。理想的指标权重能够赋予节点适合的优先级,有助于进行有效的集群资源调度,从而提升集群性能,减少用户作业执行时间。为了更直观地展示评价指标的权重对于集群性能的影响,本文采用文献[20]中的算法,进行了一组对比实验。实验仅调整了节点性能指标体系中静态因素和动态因素的权重,其他实验配置完全一致。实验结果如表1所示。

表1 节点评价指标权重变化对任务完成时间的影响
从表1可以看出,当节点评价指标权重发生变化时,集群完成相同用户作业的时间差距较为明显。因此非常有必要研究如何更为合理地确定节点优先级评价体系中各指标的权重,从而完成节点优先级的优化。
目前对于优先级评价指标体系中各指标的权重进行优化的研究相对较少。层次分析法[29](analytic hierarchy process,AHP)是一种经典的权重计算方法,但是它的计算结果存在主观性较强的缺点。节点优先级评价指标权重的确定是比较繁杂的非线性工程,需要建立权重的学习机制,可以通过具有学习、记忆、归纳、容错及自适应能力的人工神经网络[30-31](artificial neural network, ANN)予以解决。因此,本文实验平台基于中央处理器(central processing unit, CPU)异构进行验证和说明,文中将层次分析法和BP神经网络[32-33]有机地结合在一起,提出了基于AHP-BP神经网络模型[34]的集群节点优先级的优化算法。该算法首先采用AHP确定节点优先级的评价指标体系,并计算出各指标的初始权重。然后建立BP神经网络评价模型并进行网络训练。训练好的BP神经网络能够提供更加科学有效的指标权重以优化节点的优先级。
1 构建Spark集群节点优先级评价指标体系
AHP是一种解决多因素多目标问题的决策方法,由美国运筹学家Saaty教授于20世纪70年代首先提出[35-36]。它是将定性与定量相结合的系统分析方法,是一种能将复杂系统的决策思维过程模型化、数量化的方法。AHP根据系统多目标要求,把多目标分解成多层次因素,依据因素间关系建立层次结构,进行因素间重要性的两两对比,结合专家打分进行各因素重要性排序从而确定各因素的权重。
1.1 建立递阶层次结构
AHP的工作流程如图1所示。

图1 层次分析法的工作流程Fig.1 Workflow of AHP
根据前人文献进行综合分析,本文建立了集群节点优先级评价指标体系,包括2个评价因素、8个评价指标(属性)。
1)静态因素(B1):
①CPU速度(C1) : CPU的时钟频率。计算机的运行速度一般可以由它决定。
②CPU核数(C2):一个CPU核心的数目。在其他配置相同的条件下,核心数目越多,CPU的运转速度越快,机器的性能越好。
③内存容量(C3):节点内存的大小会对Spark的运行效率起到决定性作用。
④磁盘容量(C4):集群运行过程中进行数据的存储及软件的存储。
2)动态因素(B2):
①CPU剩余率 (C5):表示节点核心的忙闲情况。CPU剩余率过低则该节点可用资源很少,需要等资源释放后才可以继续任务的运行。
②内存剩余率 (C6):内存对于集群运行起着极其重要的作用。
③磁盘剩余率 (C7):磁盘用于数据存储。
④CPU负载 (C8):在一段时间内CPU正在处理及等待CPU处理的进程数之和,即CPU使用队列长度。
节点优先级评价指标体系为三层结构模型:目标层(A)、一级指标层(B)和二级指标层(C),如图2所示。

图2 节点优先级评价指标递阶层次结构Fig.2 Hierarchical structure of node priority evaluation
1.2 计算权重
1.2.1 构造判断矩阵
经过专家打分,得到各判断矩阵,如表2~4所示。表2给出了一级指标判断矩阵A-B。

表2 一级指标判断矩阵A-B
二级指标的判断矩阵分别为B1-C(如表3所示)和B2-C(如表4所示)。

表3 二级指标判断矩阵B1-C

表4 二级指标判断矩阵B2-C
计算指标单权重,求得二级指标层C对一级指标层B1的权重向量为:

=[0.113,0.173,0.641,0.073]T
(1)
为进行矩阵的一致性检验,计算出一致性指标CI=0.015 3。表5给出了不同阶数的矩阵所对应的平均随机一致性指标RI的标准值。

表5 平均随机一致性指标RI
四阶判断矩阵对应的RI为0.90,则一致性比率CR=CI/RI=0.017<0.10,满足一致性检验。同理可求得另外两个权重向量如下:
(2)
(3)
这两个向量都满足一致性检验。
1.2.2 计算综合权重
使用式(1)~(3),可以得到各评价指标对目标层的综合权重向量为:
W=[0.033 9, 0.051 9,0.192 3,0.021 9,
0.109 2,0.295 4,0.054 6,0.241 5]T
(4)
此向量也满足一致性检验。
2 建立Spark集群节点优先级评价神经网络模型
由于需要通过专家打分确定判断矩阵,AHP存在一定的主观性和误差。可以利用人工神经网络对AHP得到的权重进行优化,从而获得更加客观有效的节点优先级评价体系。
2.1 BP神经网络
人工神经网络[37-38]是非线性、自适应、自组织的网络系统。本文采用的神经网络模型为BP神经网络[39-42],它是一种误差反向传播的多层神经网络,是理论研究比较成熟、应用最为广泛的神经网络之一。图3给出了BP网络模型。

图3 BP网络模型Fig.3 BP network model
2.2 BP神经网络的学习算法
BP网络的学习算法框架如图4所示。

图4 BP网络学习算法框架Fig.4 Framework of BP network learning algorithm
Step1:设置初始参数wij和θ。wij表示输入层与隐含层的权系数或隐含层与输出层的权系数,i表示输入层或隐含层输入节点,j表示输出节点,θ表示隐含层各神经元偏置或输出层各神经元偏置。初始设置范围为[0,1]。设定计算精度值ε和最大迭代次数M。
Step2:将数据样本添加至网络中,利用式(5)计算输出值yj:
yj=(1+e-x)-1
(5)
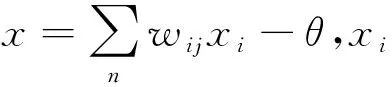
Step3:将已知输出数据dj与计算得到的输出数据进行差值计算,得到两者之间的误差Δj=dj-yj,再根据式(6)计算调整权系数的调整量:
Δwij=ησjxi
(6)
其中,η为比例系数,即学习率,范围为[0,1],一般设置为0.01或者0.05,具体取值根据实际情况决定。在神经网络中可通过逐步提高η的值进行训练,以得到稳定且精度较高的网络。σj表示输出误差相关值。
σj=ηj(1-yj)(dj-yj)=ηjΔj(1-yj)
(7)
BP神经网络的反向误差传播使用式(8)进行:
(8)
其中,m表示输出层神经元数。
各层神经元的权重调整后结果用式(9)计算得到(其中t表示学习次数):
wij(t)=wij(t-1)+Δwij
(9)
BP学习算法不断迭代,对wij值进行调整,直到输出的误差小于允许的误差值ε或是达到迭代次数M,则网络模型训练成功。BP算法通过迭代算法求得权重。
2.3 AHP-BP神经网络模型
基于AHP-BP神经网络模型的Spark集群节点优先级评价算法包括三个部分:数据获取和处理、三层BP神经网络模型的建立、神经网络训练和节点优先级评价指标权重的计算。
2.3.1 数据获取和处理
1)节点优先级的初步计算:利用AHP计算评价指标体系中各指标的初始权重。
2)节点实时数据的获取:在Spark集群中进行任务运行,同时利用Ganglia[43-45]实时获取集群节点的资源数据。

4)初始节点优先级的计算:使用初始权重和归一化后的节点数据计算出节点对应的优先级,此优先级作为神经网络训练样本的输出。
2.3.2 三层BP神经网络模型建立
本文建立的BP神经网络模型分为三层结构,即输入层、隐含层和输出层。通过不断迭代训练使其收敛可以得到稳定的网络结构和参数。
1)输入层节点的选择:输入节点个数与评价指标的个数相对应。由图2可知,评价指标体系共有8个评价指标,因此神经网络的输入层节点数n=8。
2)输出层节点的选择:节点的优先级数值是网络的唯一输出,因此输出层节点数为1,即m=1。使用式(4)给出的权重可以计算得到对应的神经网络输出值。
3)隐含层节点的选择:隐含层节点的选择非常关键,因为它会极大影响BP神经网络的精确度和学习效率[46]。然而,到目前为止并没有可指导的理论,只能在总结前人文献知识的基础上,根据经验和问题的实际情况而定。通常可以使用式(10)和式(11)来获得隐含层神经元数的大致范围进而确定隐含层的神经元数S。
(10)
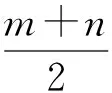
(11)
其中,n是输入层神经元数,m是输出层神经元数,α是[1,10]之间的整数。通过计算,本文建立的神经网络模型中隐含层神经元数S的取值范围为[5,8]。
决定系数R2能够评判神经网络模型预测能力的好坏,因此可用来确定隐含层神经元的数目。R2的计算方法如式(12)所示。
(12)

使用式(12)和实际样本的实验测试结果,就可以确定合适的隐含层神经元数。隐含层神经元数取值范围为[5,8],因此设定隐含层神经元数分别为5、6、7、8,依次进行数据训练得到对应网络的R2。实验结果如表6所示。

表6 隐含层神经元数和对应的R2
由表6可知,当隐含层神经元数为5时,R2=0.89,相比其他神经元的取值效果最好,所以本文模型最终选择5作为隐含层神经元数。图5(a)为节点优先级评价BP网络模型,图5(b) 给出了可视化的网络模型搭建过程。

(a) BP网络模型(a) BP network model
2.3.3 网络训练和权重计算
网络模型搭建完成后,需要收集学习样本以进行网络训练,样本的选择对于网络的训练很重要。一般需根据实际情况和网络大小来确定合适的样本数,过多或过少都会影响训练结果。依据本文中BP网络结构及Ganglia得到的节点性能参数进行实验,再根据R2的值即可确定最适合的样本容量。实验结果如表7所示。

表7 样本容量和对应的R2
从表7可以看出,样本数取160时BP神经网络具有较好的网络模型预测能力,因此本文中选取160个样本进行BP网络训练。读取160个样本数据进行量化后随机产生训练集和测试集,两者比例为15 ∶1,即150个训练样本和10个测试样本。设置训练参数迭代次数为6 000,训练要求精度即目标误差为0.001,学习率为0.01,最小梯度要求为e-10。进行网络训练达到收敛状态后获取网络训练权重数据,用矩阵表示如式(13)所示。
式(13)中,权重矩阵的前8列分别对应输入层的8个神经元,最后1列对应输出层神经元;矩阵的各行分别对应隐含层的5个神经元。Wij(i=1,2,…,5;j=1,2,…,8)表示第j个输入神经元与第i个隐含层神经元之间的权重;Wi9表示输出神经元与第i个隐含层神经元之间的权重。
获取的数据需要进行计算以得到最终权重。神经网络训练后得到的神经元权重表示各神经元之间的关系,为了得到输入因素和输出因素之间的关系,需要对得到的权重系数进行分析处理,利用以下指标[39-40]进行输入因素和输出因素关系的描述。

(13)
1)相关显著性系数:
(14)
2)相关指数:
Rij=|(1-e-rij)(1+e-rij)|
(15)
3)绝对影响系数:
(16)
其中:i为神经网络输入层神经元,i=1,2,…,n;j为神经网络输出层神经元,j=1,2,…,m;k表示神经网络隐含层神经元,k=1,2,…,p;ωjk表示输出层神经元j和隐含层神经元k之间的权重系数。通过上述公式求出绝对影响系数Sij,即为优化的节点优先级评价指标的权重。
使用式(14)~(16),得到本文中各指标的权重,如表8所示。

表8 优化后的节点优先级评价指标权重
2.4 SDASA算法简介
实验采用文献[20]中提出的基于节点优先级的Spark动态自适应调度算法(Spark dynamic adaptive scheduling algorithm, SDASA) 进行任务调度,其中集群中各个节点的优先级使用BP神经网络优化后的节点优先级评价指标权重计算。为方便读者,简要对SDASA算法进行介绍。
SDASA算法[20]的架构如图6所示,图中RPC为远程过程调用协议,是Spark使用的通信框架。

图6 SDASA算法架构[20]Fig.6 SDASA algorithm architecture diagram[20]
具体算法描述如下:
输入:任务集TaskSet,任务个数为m;集群节点集合WorkerOffer,节点个数为n。
输出:返回任务列表,即第i个任务分配到第j个节点。
Step1:启动集群,触发监控启动心跳。
Step2:利用Ganglia获取Slave节点动静态因素信息。
Step3:Master对集群每个节点进行轮询,将得到的节点的动静态因素数据存入轮询数据库中。
Step4:Master对收到的信息进行处理,计算出各节点的动静态指标值。
Step5:Master根据每个节点的动静态指标值计算得到各节点优先级。
Step6:根据各节点优先级对节点集合WorkerOffer进行排序,节点优先级越高,排序越靠前;反之,排序越靠后。
Step7:从优先级最高的节点开始,依次遍历每个节点。在每个节点轮流遍历TaskSet中的每个Task,循环执行Step 8。
Step8:获取Task在节点上的本地化参数并进行判断,如果参数是最大,执行Step 9。
Step9:分配该任务Task给该节点。
3 实验结果与分析
为了验证本文提出的节点优先级优化算法的有效性,进行了相应的实验。
3.1 实验环境
基于Spark on standalone模式,搭建两个集群进行实验。集群1中有3个节点,分别为主节点Master、从节点Slave1和Slave2。集群2中有5个节点,分别为主节点Master、从节点Slave1、Slave2、Slave3、Slave4。集群1和集群2的节点静态因素指标值分别如表9和表10所示。

表9 集群1节点静态因素指标值

表10 集群2节点静态因素指标值
3.2 BP神经网络优化的性能评价体系之权重
利用AHP计算得到的各指标初始权重如式(4)所示。实验中通过BP神经网络优化后的节点优先级计算的各影响因素权重分别为:
1)各因素综合权重如表8所示。
2)静、动态因素权重为0.371 5和0.628 5。
3)各静态因素CPU速度、CPU核数、内存容量和磁盘容量的权重分别为0.135 7、0.268 1、0.549 9和0.046 3。
4)各动态因素CPU剩余率、内存剩余率、磁盘剩余率、CPU负载的权重分别为0.284 6、0.507 0、0.145 4和0.062 8。
表11和表12分别给出了集群2中各节点的动态因素指标值随着任务运行的变化情况。实验使用了数据量为4 GB的工作负载Sort,表中CPU负载显示的是该节点任务队列的长度。优先级计算使用的是BP神经网络优化后的权重。由表可以看到,随着任务的执行,各个节点的优先级均发生了变化。
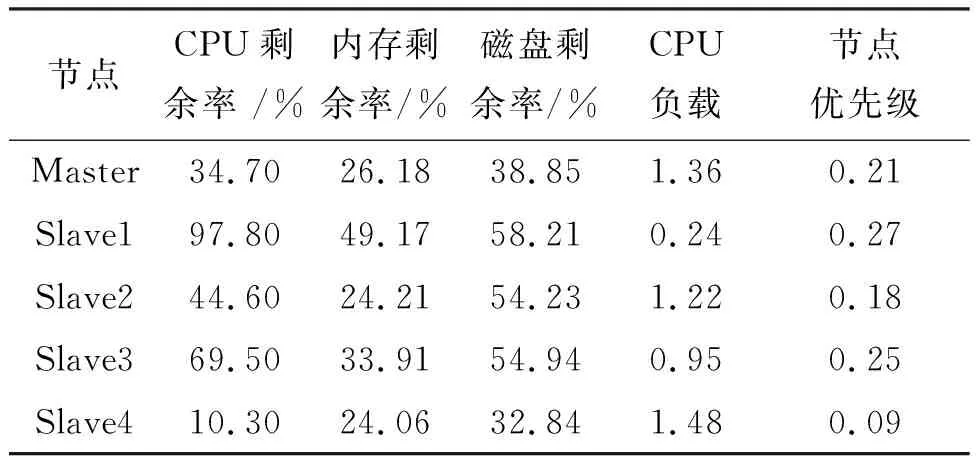
表11 任务开始时动态数据采集及节点优先级初始状态

表12 系统运行28 s后采集的各节点动态数据及节点优先级
3.3 BP神经网络权重优化调度算法实验结果及分析
本节展示节点权重优化算法的有效性,对比算法为Spark默认调度算法[47-49]和2.4节描述的基于AHP权重的SDASA算法。采用的负载是中国科学院计算技术研究所研发的基于大数据基准测试的开源性程序集BigDataBench[50-51]。实验选择了三种工作负载,分别为WordCount、Sort和K-means。
实验分别在包含3个节点的集群1和包含5个节点的集群2上进行。选取两个集群进行实验的目的是考查随着集群中节点数目的增多,节点权重优化算法对于集群性能提升的影响。两个集群上所进行的实验相同,均为相同数据量不同工作负载实验和相同工作负载不同数据量实验。为了实验数据的准确性,每种实验进行5次并记录时间,以5次的平均值为最终实验结果。
3.3.1 相同工作负载不同数据量的实验
本实验处理的工作负载是WordCount,实验使用不同数量的数据集,分别为2 GB、4 GB、6 GB、8 GB和10 GB。图7给出了集群1上的实验结果,图8给出了集群2上的实验结果。

图7 集群1上不同数据量执行时间对比Fig.7 Comparison of execution time under different data sizes for Cluster 1

图8 集群2上不同数据量执行时间对比Fig.8 Comparison of execution time under different data sizes for Cluster 2
由图7和图8可以得到,运行相同工作负载时,使用BP神经网络优化权重的SDASA与使用Spark默认算法和AHP初始权重的SDASA相比,任务的执行时间大幅缩减。表13给出了具体的对比结果。
从表13可以看到,负载相同、工作量不同时,集群1环境下,与Spark默认算法相比性能平均提升12.72%;与SDASA算法相比平均提升6.57%。集群2中,与Spark默认算法相比性能平均提升16.64%;与SDASA算法相比平均提升9.76%。随着集群中节点数目的增加,节点优先级优化后,集群的性能提升也更加显著。
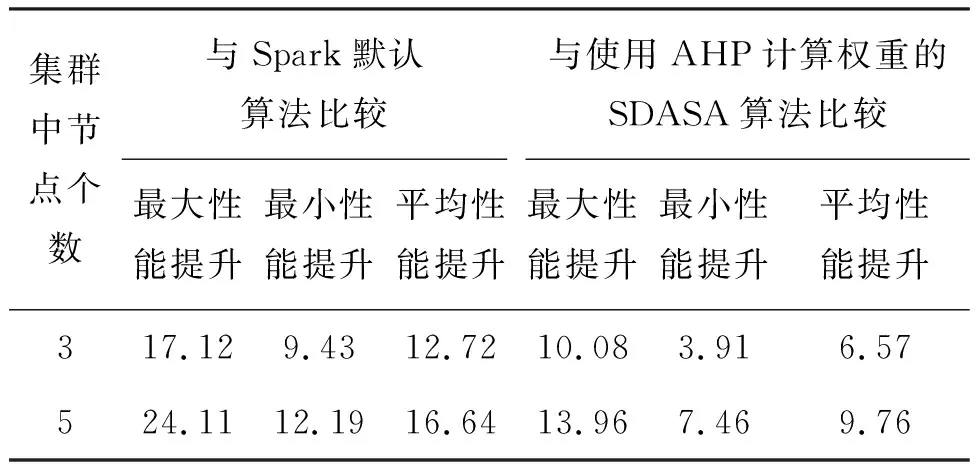
表13 不同数据量时集群性能对比
3.3.2 不同工作负载相同数据量的实验
为了考察节点性能优先级评价指标的权重对于不同性质任务的影响,对三种不同工作负载进行了实验,所选负载分别为WordCount、Sort和K-means,实验使用的数据量均为2 GB。使用Spark默认的任务调度算法、基于AHP权重的SDASA和本文基于AHP-BP权重的SDASA得到的实验结果分别如图9和图10所示。

图9 集群1上不同工作负载执行时间对比Fig.9 Comparison of execution time under different workloads for Cluster 1

图10 集群2上不同工作负载执行时间对比Fig.10 Comparison of execution time underdifferent workloads for Cluster 2
由图9和图10可以看出,进行节点优先级优化后的SDASA与Spark默认调度算法和使用AHP初始权重的SDASA相比,运行WordCount、Sort和K-means三种工作负载时,系统性能都有提升。具体数据见表14。

表14 不同工作负载时集群性能对比
从表14可以看到,当处理相同工作量的不同负载时,集群1环境下,与Spark默认算法相比性能平均提升11.90%,与SDASA算法相比平均提升4.30%;集群2中,与Spark默认算法相比性能平均提升12.49%,与SDASA算法相比平均提升6.54%。同样地,集群的性能提升会随着集群中节点数目的增加而增加。因此可以看出,随着集群规模的进一步加大,本文提出的优先级调优算法能够更好地提高集群性能。
4 结论
为了解决分布式异构集群性能优化问题,本文对集群节点的优先级进行了优化。本文建立了AHP-BP神经网络模型,利用AHP和BP神经网络来确定集群节点优先级评价指标体系中各因素的权重。实验结果表明,使用所提出的节点优先级调优算法能够得到合理的集群节点优先级,提升Spark集群系统性能。
下一步的研究工作将从以下几个方面展开:
1) 本文模型考虑的异构集群的复杂度主要体现在同一集群的多个节点之间在磁盘容量、CPU核数和速度以及内存容量等方面存在较大差异,从而导致节点计算能力的不同。本文提出的基于AHP-BP神经网络的节点优先级评价模型具有较强的通用性。目前文中的AHP层次结构是针对上述的异构模型所建立的。当考虑更为复杂的异构集群,如CPU-GPU-NPU等不同类型的异构时,可以将GPU及NPU的速度、核数、剩余率、负载等因素也作为影响节点性能的因素加以考虑,建立新的AHP层次结构模型。同时根据新的节点性能影响因素调整BP神经网络的输入,训练符合新AHP模型的BP网络模型。因此后续将研究本文提出的算法对于其他种类异构集群的有效性。
2) 研究更好的学习样本选择方法。
3) 选用更合适的神经网络或深度学习方法进行实验研究。
4) 搭建大型集群,针对大数据量和多种负载进行更多的实验,以进一步验证优先级优化算法的有效性。

