基于胡聿贤谱的带支撑广义Maxwell 阻尼隔震结构随机响应分析1)
邹万杰 刘美华 李创第 葛新广
(广西科技大学土木工程学院,广西柳州 545006)
引言
减隔震联用技术已广泛应用于桥梁、铁路、建筑结构等土木工程领域,隔震装置可以延长结构自振周期,阻尼器消耗地震能量,在基础隔震层设置阻尼器能抑制隔震层和上部结构可能发生的过大位移,有效减小建筑结构地震响应[1-3].黏弹性阻尼器耗能能力强,为了精确模拟黏弹性阻尼器的本构关系,国内外研究人员提出了各种黏弹性阻尼器力学模型,包括Maxwell 模型[4]、一般积分模型[5]、分数导数模型[6-7]、广义Maxwell 模型[8]等.其中广义Maxwell 模型由多个Maxwell 单元和一个弹簧单元并联组成,各Maxwell 单元有不同的弹簧模量和黏壶黏度,因而具有不同的松弛时间,能更完善地模拟黏弹性阻尼器的力学松弛行为[9-10].阻尼器常通过消能支撑连接于建筑结构,支撑是保证结构有效耗能的重要构件,当地震作用时,阻尼器和支撑都能起到消能减震作用[11-13].
地震地面运动具有随机性,时域法和频域法是目前求解随机地震响应的两种主要方法[14-16].当地震动功率谱根据Fourier 变换转化为其相应协方差函数表示时,用时域法分析有时更容易获得随机地震响应的解.在工程中常用的地震动随机激励模型中,白噪声模型由于在数学上的简单性,更容易获得协方差函数[17],白噪声模型假设在整个地震过程中地震动各频率成分强度是恒定的,并不能准确反映地震动的频谱特征.Kanai-Tajimi 模型过分夸大低频地震动能量,不适用于低频结构的随机地震响应分析.胡聿贤模型[18]通过引入低频减量参数,将Kanai-Tajimi 谱的特低频部分进行合理弱化处理,从而使功率谱密度函数在零频处不再有奇异点,且满足连续两次可积的条件,保证了导出的地面速度方差和地面位移方差有界,因此,采用胡聿贤模型模拟随机地震作用更具有合理性.胡聿贤模型协方差函数比较复杂,但可通过滤波方程将胡聿贤谱激励等效转化为白噪声激励求解地震响应,从而解决胡聿贤模型直接用于时域分析难于求解的问题,再由Dirac 函数的性质,应用时域法分析基于白噪声激励的动力响应将得到极大简化[19-20].
复模态法是常用的时域分析方法,复模态法可以将系统精确解耦为独立的复模态变量方程[21-23],虚拟激励法和传递函数法是频域分析的两种代表性方法.虚拟激励法计算结构响应需对功率谱从零到无穷大范围内进行积分[24-25],传递函数法利用拉普拉斯变换,获得结构特征值与特征向量,从而在非扩阶系统中得到瞬态响应的解析解[26].谱矩和方差是结构抗震设计的重要参数[27-29],利用复模态法求解结构地震响应需要扩阶,扩阶之后会因变量个数剧增而使计算效率变低,虚拟激励法和传递函数法计算得到的谱矩表达式含积分项,需逐步积分计算确定谱矩值,会因积分步长和积分区间选择不唯一导致计算结果具有不确定性,从而会影响计算精度.
为此,本文为了同时提高在胡聿贤谱激励下带支撑广义Maxwell 阻尼隔震结构动力响应分析的精度与效率,基于复模态法的精确性,并且兼顾扩阶之后的计算效率,通过重构结构运动方程,再运用复模态法解耦该联立方程,最后通过简化系统响应协方差表达式,得到系统响应功率谱和谱矩表达式,从而提出了一种扩阶之后简明的结构响应解析分析方法.与虚拟激励法结果进行对比,验证了系统响应功率谱和0~2 阶谱矩的正确性.
1 隔震系统的运动方程
1.1 结构运动方程
设上部n层结构的质量、刚度、阻尼矩阵分别为M,K,C,每层层间质量、刚度、阻尼分别为mi,ki,ci(i=1,2,···,n);隔震层的质量、刚度、阻尼分别为mb,kb,cb;隔震层设置带支撑广义Maxwell 阻尼器PG(t),隔震层相对地面位移为xb,上部结构相对隔震层的位移为x.在随机地震激励x¨g(t) 作用下,基础耗能隔震结构力学模型如图1 所示,上部结构与隔震层的运动方程分别为
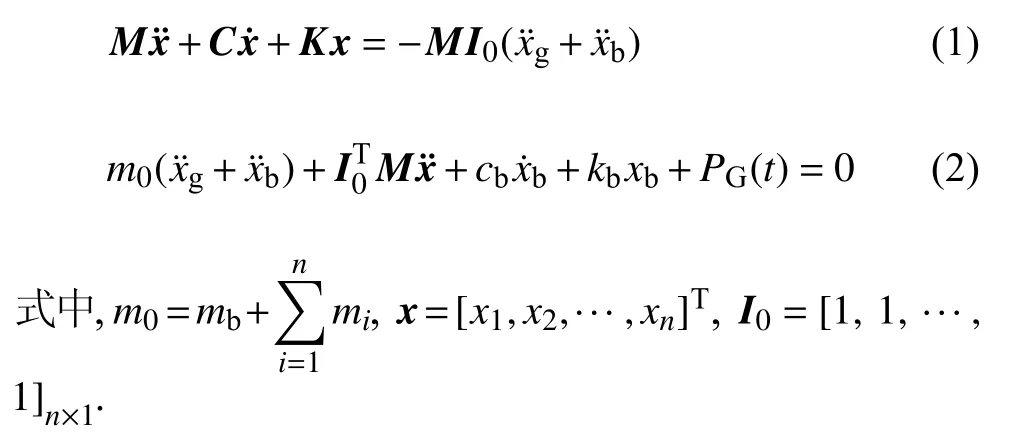
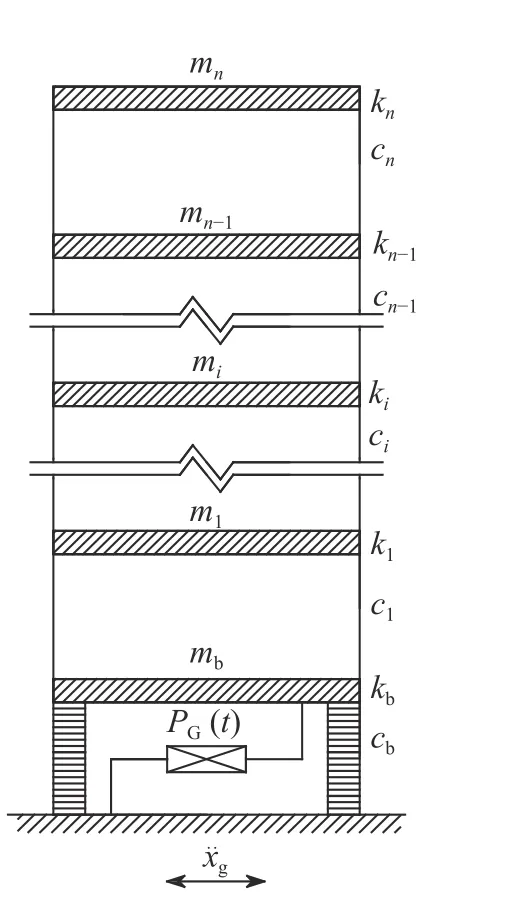
图1 基础耗能隔震结构力学模型Fig.1 Mechanical model of base energy dissipation isolated structure
1.2 带支撑广义Maxwell 阻尼器等效本构关系
广义Maxwell 阻尼器由一个线性弹簧单元和多个Maxwell 阻尼单元并联组成,该模型参数足够多,对黏弹性阻尼器本构关系试验拟合精度高.广义Maxwell 阻尼器与支撑串联设置在隔震层,将整体串联系统作为等效阻尼器,以考虑支撑刚度对结构响应的影响,带支撑广义Maxwell 阻尼器力学模型如图2 所示.由于阻尼器与支撑串联连接,故支撑受力Pd(t)、广义Maxwell 阻尼器受力PQ(t)[8]与等效阻尼器受力PG(t) 三者相等,力的平衡关系为
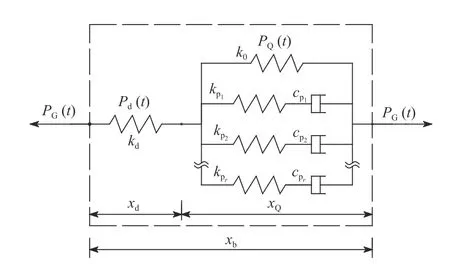
图2 带支撑广义Maxwell 阻尼器力学模型Fig.2 Mechanical model of generalized Maxwell damper with braces

式中,kd和k0分别为支撑刚度和广义Maxwell 阻尼器平衡刚度;xd和xQ分别为支撑位移和广义Maxwell 阻尼器位移;pj为第j个Maxwell 阻尼单元的阻尼力;j=1,2,···,r,r为广义Maxwell 阻尼器中标准Maxwell 阻尼单元的个数.
阻尼器位移xQ与隔震层位移xb和支撑位移xd之间满足如下关系

由式(3)、式(5)和式(6),得阻尼器位移为

将式(7)代入式(4),得等效阻尼器受力PG(t) 为
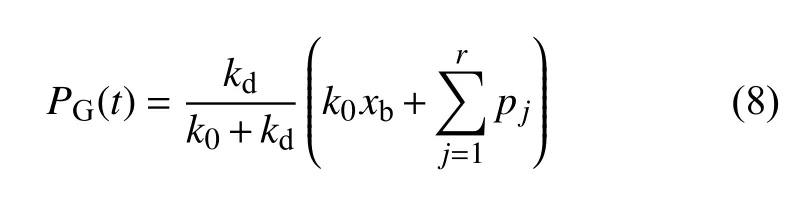
将式(8)代入式(7),阻尼器位移xQ可改写为
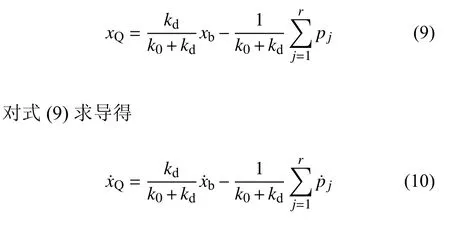
广义Maxwell 阻尼器中,各Maxwell 阻尼单元微分本构关系为[8]
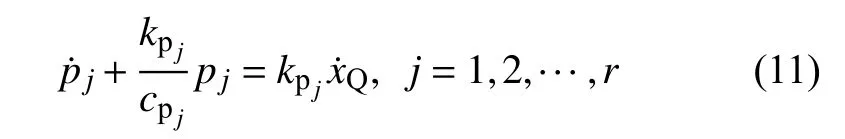
将式(10)代入式(11),将式(11)改写为
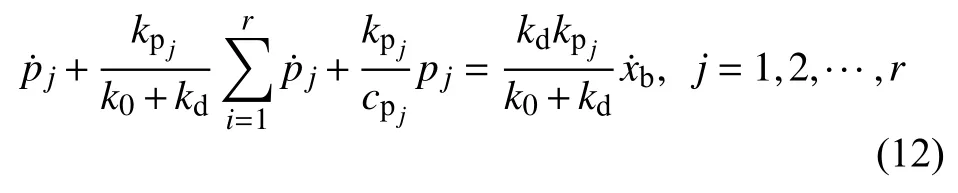
为了便于后续复模态扩阶,将式(12)写成矩阵形式
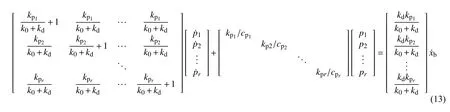
将式(13)进一步简写为

1.3 重构运动方程
胡聿贤谱在零频处不存在奇异点,因此,导出的地面均方速度和均方位移有界,胡聿贤谱滤波方程描述如下[18]
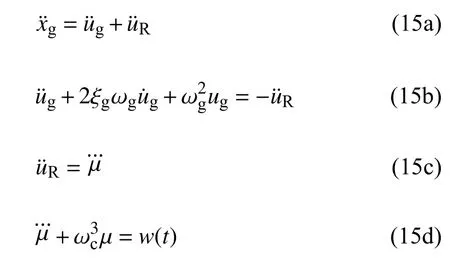
式中,为基岩运动的绝对加速度分别为地面相对基岩运动的加速度、速度和位移; ξg和ωg分别为基岩以上场地土的阻尼比和卓越频率;μ为中间变量为对 μ 求三次导数; ωc 为低频截止频率; w(t) 为白噪声随机过程.根据式(15),将原上部结构运动方程式(1)改写为式(16);根据式(8)和式(15),将原隔震层运动方程式(2)改写为式(17)
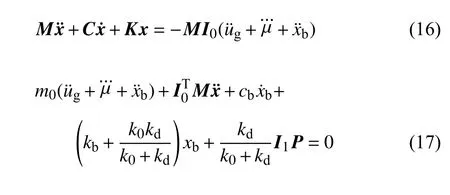
式中,I1=[1,1,···,1]1×r.
引入状态变量
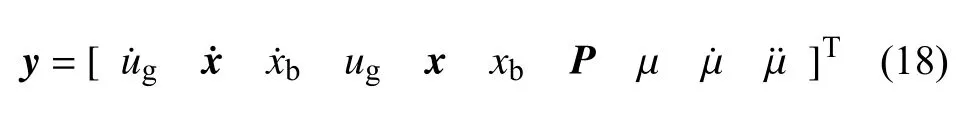
联立阻尼器微分本构方程式(14),胡聿贤谱滤波方程式(15)、结构运动方程式(16)和式(17),得到非经典阻尼系统
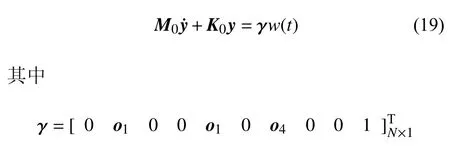
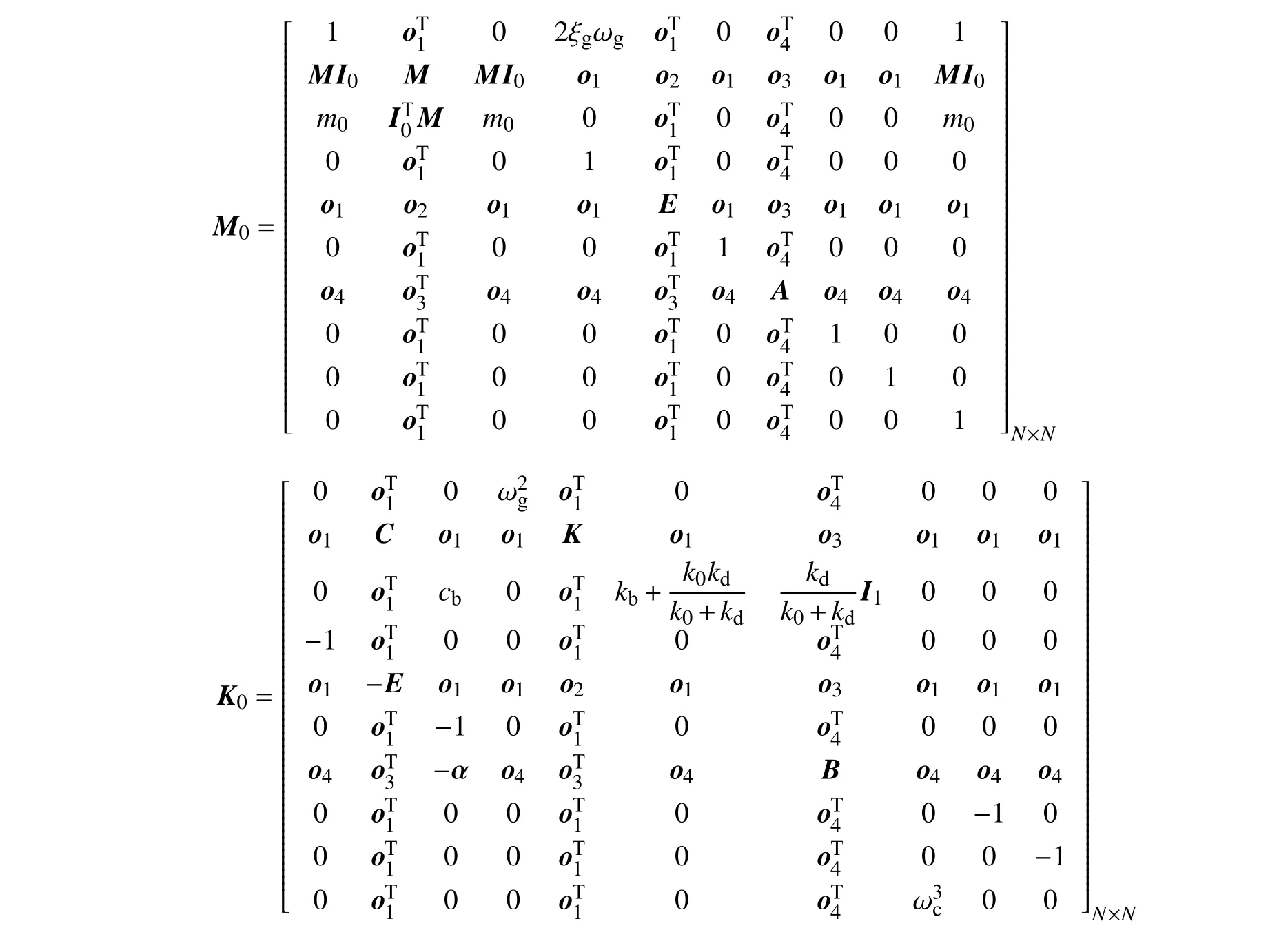
式中,o1为元素均为 0 的n×1 阶向量;o2为元素均为0的n×n阶矩阵;o3为元素均为 0 的n×r阶矩阵;o4为元素均为 0 的r×1 阶向量;E为n阶单位矩阵;N=2n+r+7,N为矩阵M0和K0的阶数,n为楼层总数,r为标准Maxwell 阻尼单元的个数.
2 系统响应的Duhamel 积分表达式
采用复模态法求解式(19),矩阵M0和K0可由右特征向量矩阵U和左特征向量矩阵V对角化,系统的特征值构成一个对角矩阵q,q满足关系
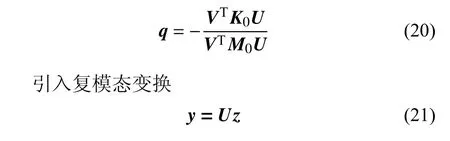
式中,z为广义复模态变量.
将方程(19)化为如下形式
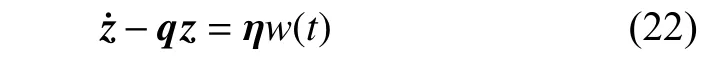
式中,η=(VTM0U)-1VTγ.
由于q为对角矩阵,且z中的元素相互独立,式(22)可以写为具有独立复模态变量的一阶方程分量形式
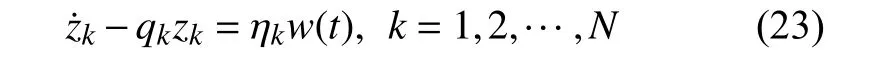
式中,zk,qk和 ηk分别为z,q和 η 的第k个分量.
已经通过滤波方程式(15)将胡聿贤谱激励等效转化为基于白噪声激励来表示,由于白噪声激励功率谱表达式简单,更容易获得协方差函数,当地震动激励相关函数可以用解析函数表示时,用Duhamel积分法求解更易于得到系统动力响应的解析解.因此,用Duhamel 积分法求解式(23),式(23)的Duhamel积分表达式为
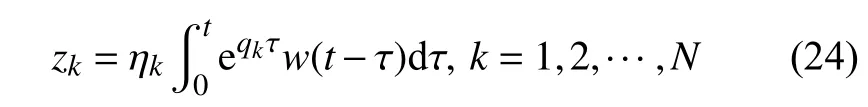
根据式(18)、式(21)和式(24),通过状态变量y中不同行对应的响应模态uj,可求得上部结构、隔震层、阻尼器以及支撑系列响应的Duhamel 积分表达式,如式(25)~式(35)和式(37)~式(39)所示.
上部结构第i层相对于隔震层的位移xi和速度x˙i的Duhamel 积分表达式为
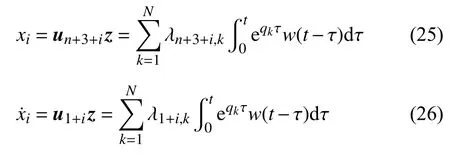
式中,ul(l=n+3+i,1+i)为右特征向量矩阵U的第l行向量; λl.k为系统响应的模态强度系数,λl,k=ul,kηk;i=1,2,···,n,n为上部结构的楼层总数.
隔震层相对于地面的位移xb和速度的Duhamel积分表达式为
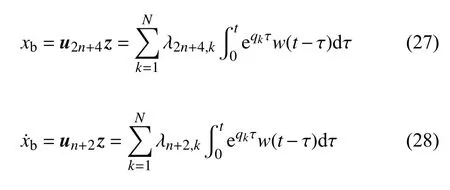
上部结构第i层的层间位移 Δxi和层间速度Δx˙i的Duhamel 积分表达式为

上部结构第i层的层间位移角 θi和层间位移角变化率的Duhamel 积分表达式为
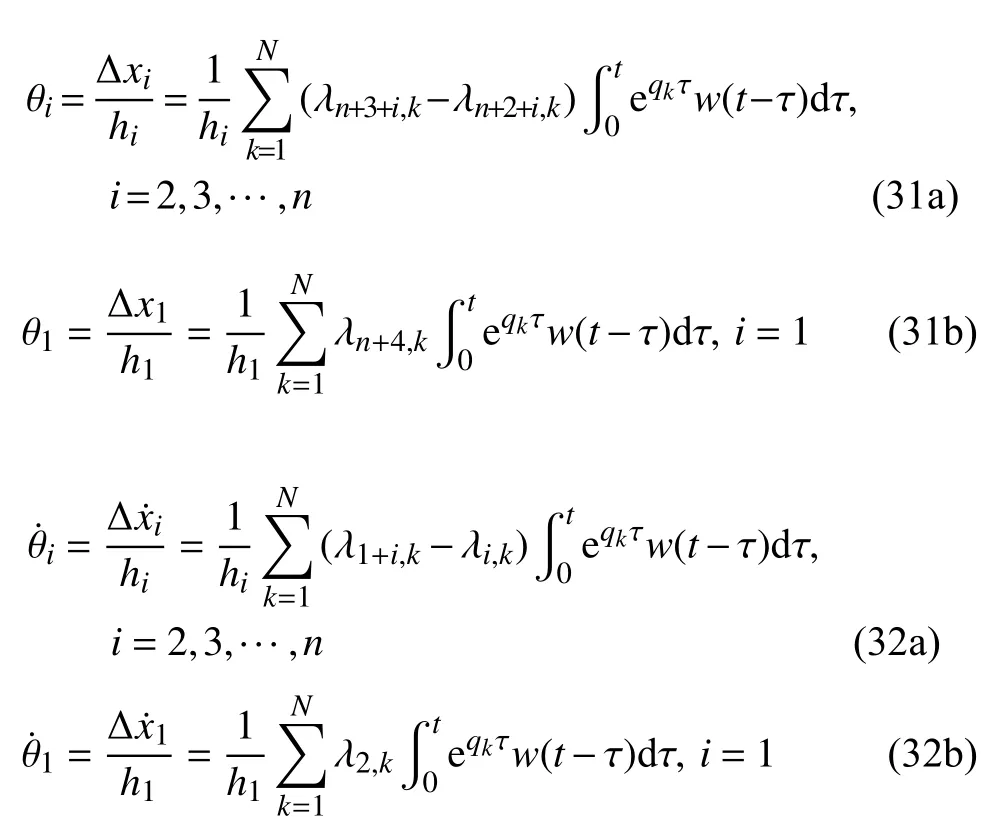
式中,hi为结构第i层的楼层高度.
由式(8),等效阻尼器阻尼力PG的Duhamel 积分表达式为
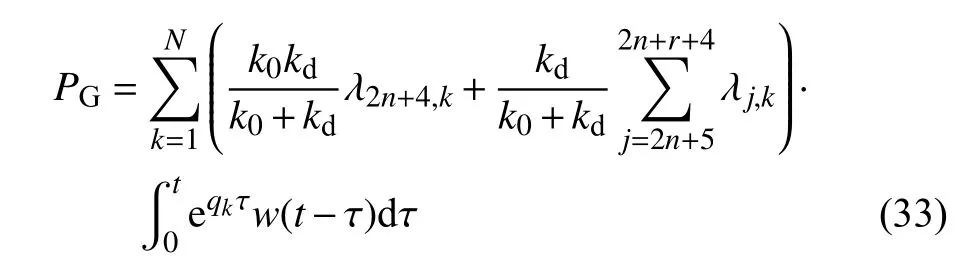
由式(3)、式(5) 和式(33),支撑位移xd的Duhamel 积分表达式为
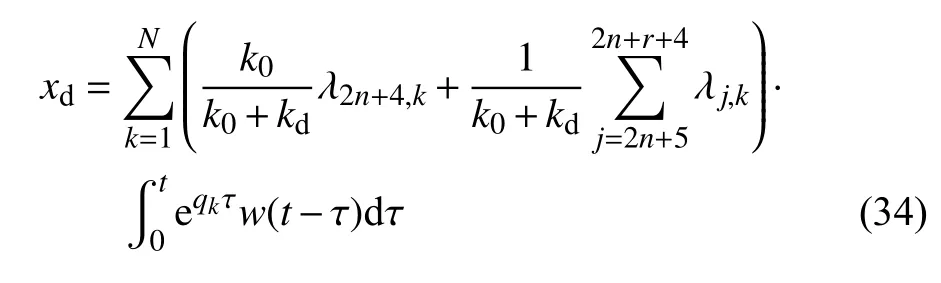
将式(27)和式(34)代入式(6),得阻尼器位移xQ的Duhamel 积分表达式为
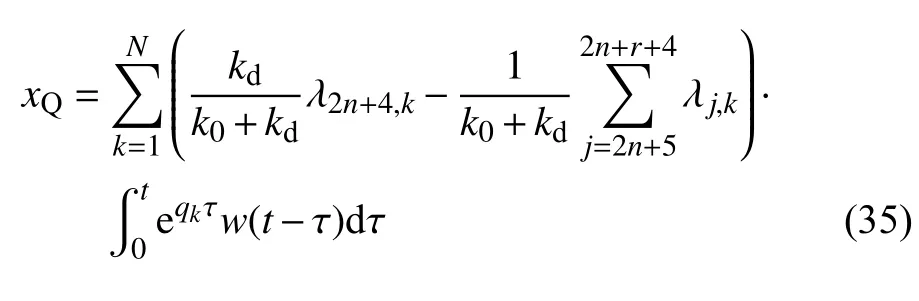
将式(11)代入式(10),阻尼器位移变化率可表示为
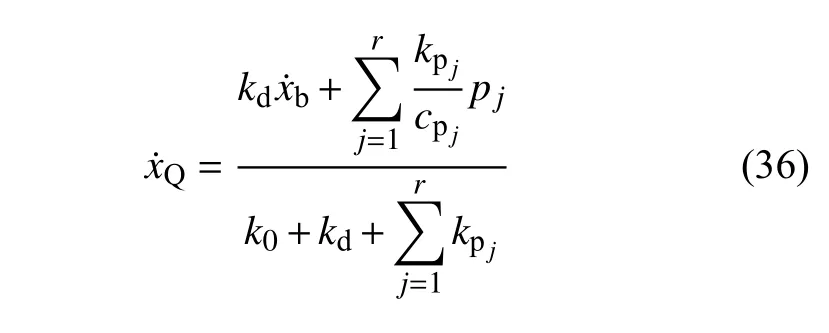
将式(36)写成Duhamel 积分形式
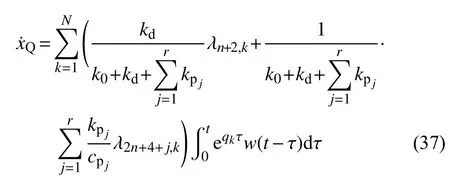
由式(6)、式(28)和式(37),支撑位移变化率的Duhamel 积分表达式为
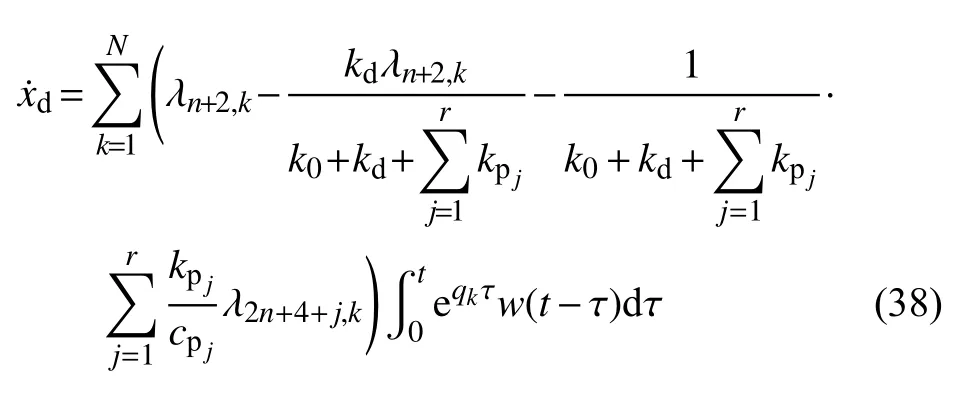
由式(3)、式(5)和式(38),阻尼力变化率的Duhamel 积分表达式为
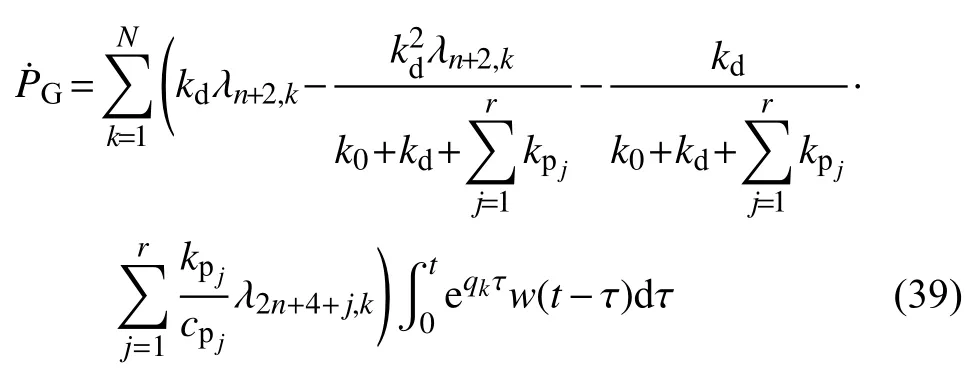
上述系列响应式(25)~式(35)及式(37)~式(39)均为Duhamel 积分形式,仅各个响应模态强度系数不同,故将它们写成统一表达式
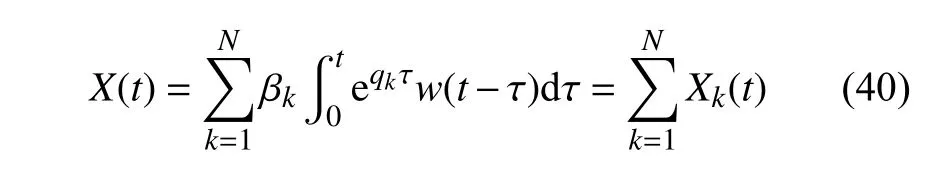
式中,Xk(t) 为X(t) 的响应分量,其表达式为
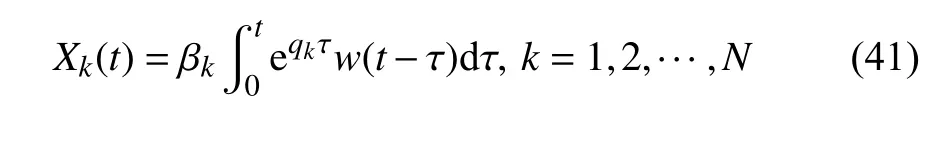
式中,βk为系统响应X(t) 对应的模态强度系数,系统系列响应模态强度系数 βk的具体解析表达式如式(42a)~式(48b)所示.统一变量符号 βk可分别指下文的
上部结构第i层相对隔震层位移xi和速度的模态强度系数分别为
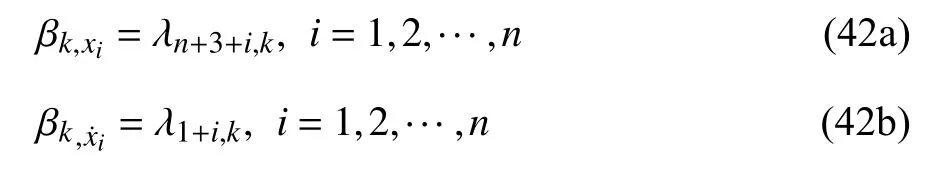
隔震层相对地面位移xb和速度的模态强度系数分别为
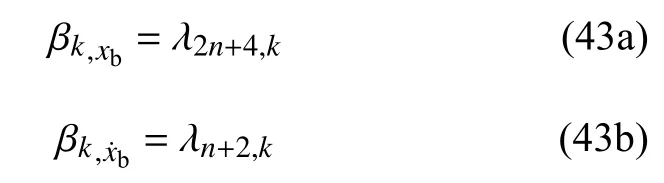
上部结构第 层层间位移 Δxi和层间速度的i模态强度系数分别为
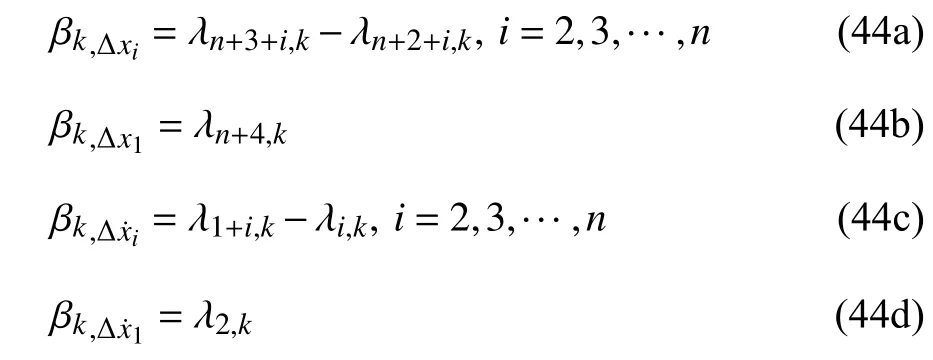
上部结构第i层层间位移角 θi和层间位移角变化率的模态强度系数分别为
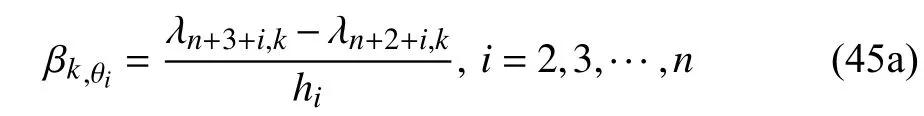
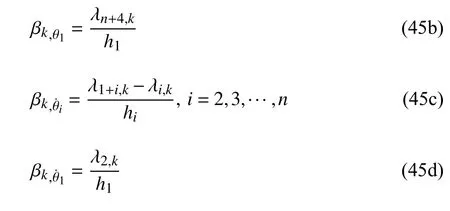
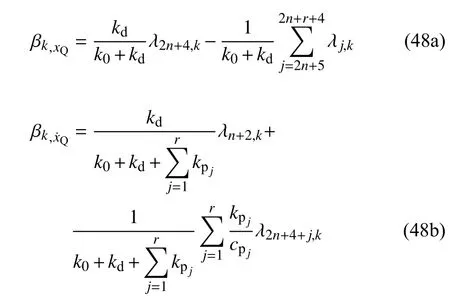
阻尼器阻尼力PG和阻尼力变化率的模态强度系数分别为
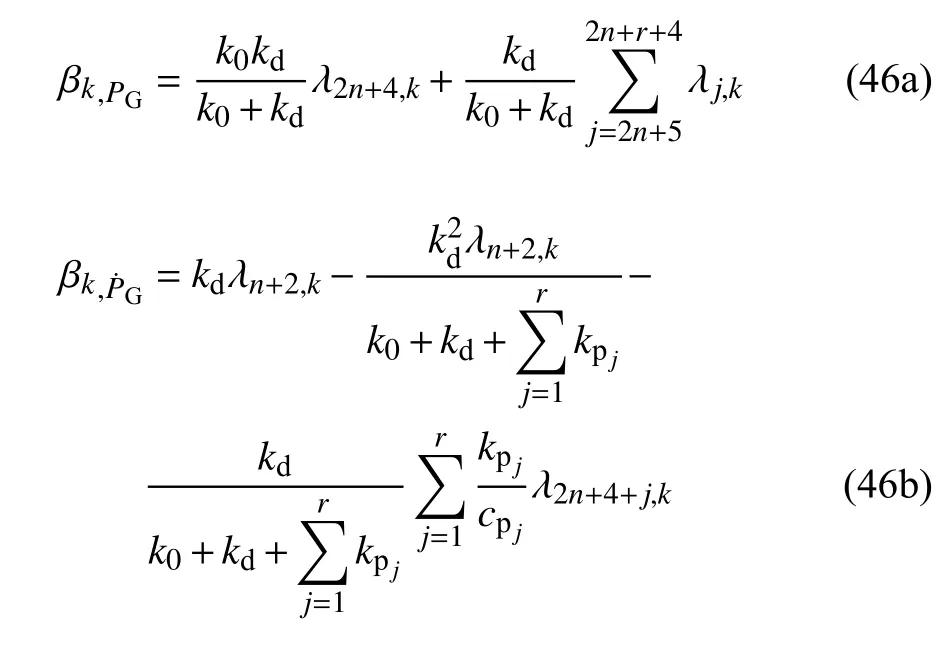
支撑位移xd和支撑位移变化率的模态强度系数分别为
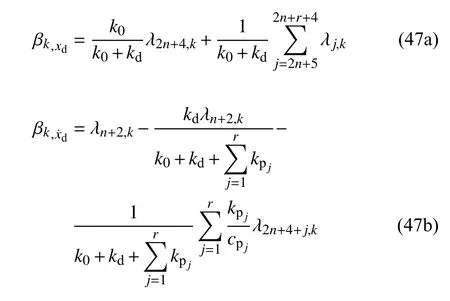
阻尼器位移xQ和阻尼器位移变化率的模态强度系数分别为
3 响应方差
根据随机振动理论[17],响应X(t) 的协方差可表示为
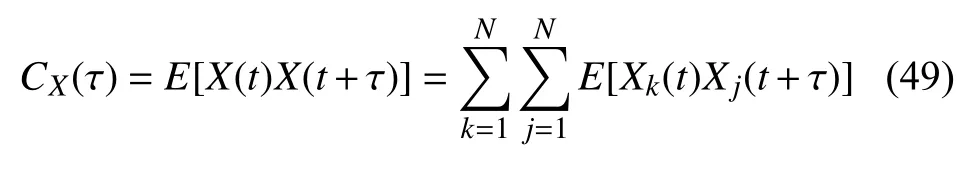
式中,E[·] 为数学期望.
将式(41)代入式(49),得系统响应分量的协方差为
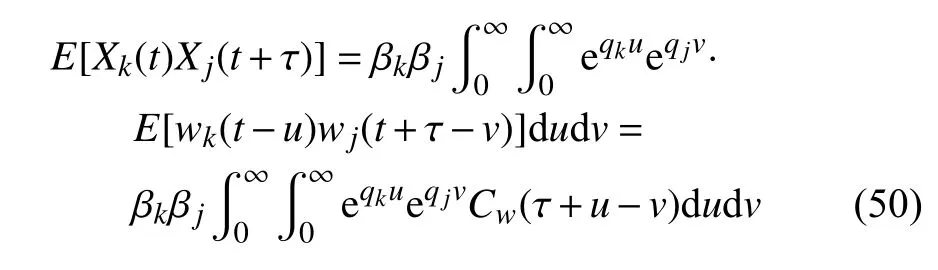
要进一步对式(50) 求积分,必须先得到激励w(t)的协方差表达式,由于w(t) 是白噪声随机过程,故其协方差函数可表示为

式中,δ(·) 为Dirac 函数.
将式(51)代入式(50),可将式(50)重写为
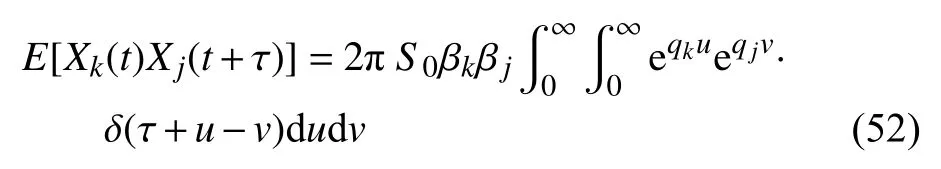
利用Dirac 函数的性质,对式(52)的积分部分进行运算可得
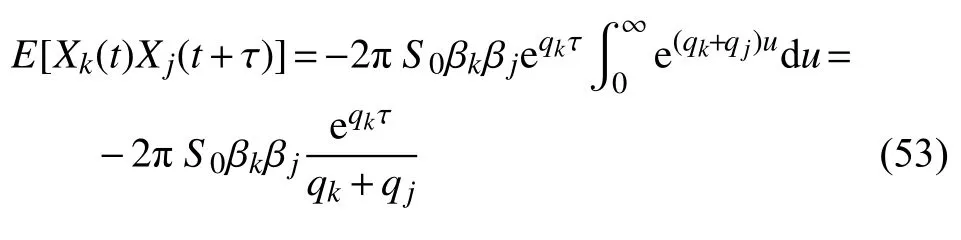
将式(53)代入式(49),系统响应X(t) 的协方差最终可简化为
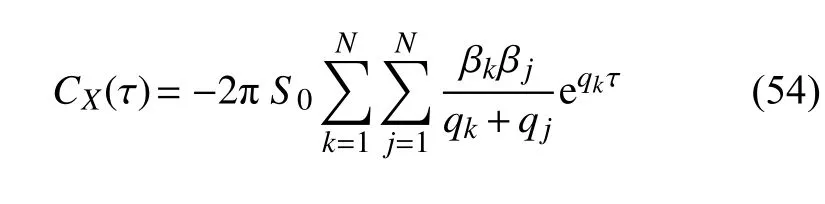
令式(54)中 τ=0,即得系统响应方差
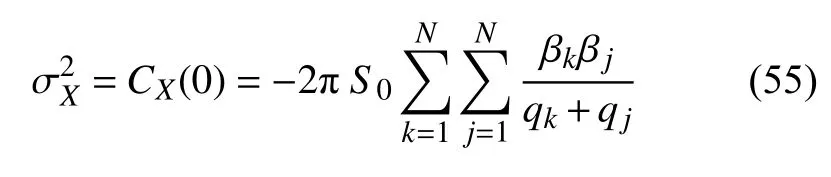
式中,βk与 βj的具体表达式详见式(42a)~式(48b).将式(42a)~式(48b)分别代入式(55),可得系统系列响应方差.
4 响应功率谱与谱矩
根据Wiener-Khinchin 关系[17],平稳随机过程功率谱密度是其相应协方差函数的Fourier 变换,即
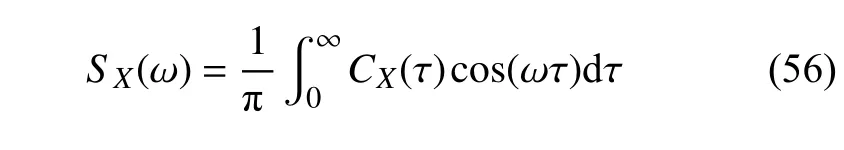
将式(54)代入式(56)并对积分部分进行运算,得系统系列响应功率谱SX(ω) 为
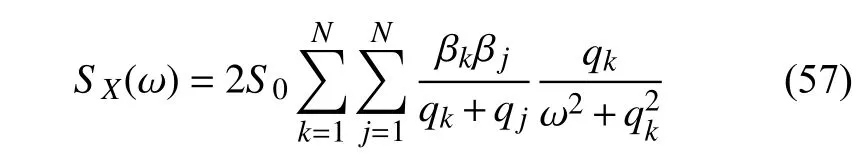
式中,βk与 βj的具体表达式详见式(42a)~式(48b).将式(42a)~式(48b)分别代入式(57),可得系统系列响应功率谱函数,例如,将式(42a)代入式(57),可得上部结构第i层楼的位移功率谱表达式为:Sxi=
系统响应的i阶谱矩 κX,i定义为[17]
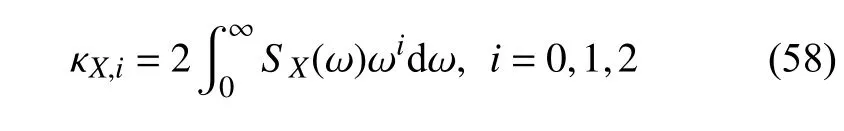
令式(58)中i=0,并对积分部分进行运算,得系统响应的0 阶谱矩为
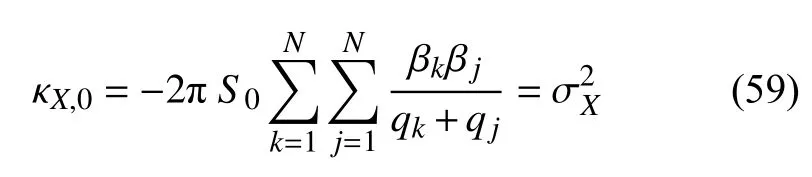
根据随机振动理论[17],系统响应的方差等于0 阶谱矩,式(59)验证了本文方法的正确性.系统响应的2 阶谱矩等于相应变化率的0 阶谱矩,因此,系统响应的2 阶谱矩可表示为
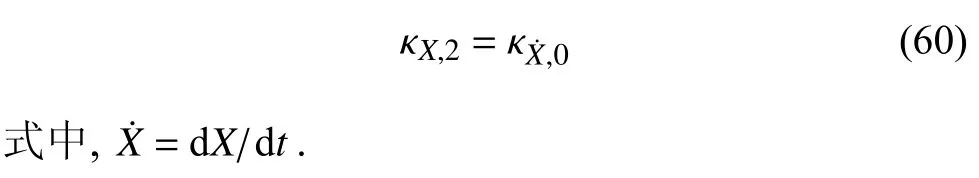
令式(58)中i=1,可得系统响应的1 阶谱矩为
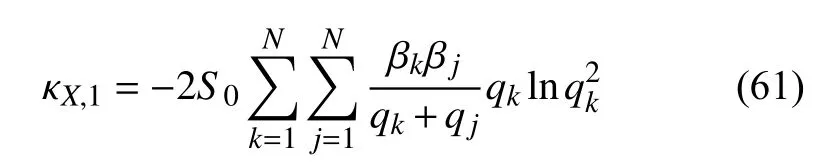
计算0 阶谱矩和1 阶谱矩时,βk与 βj的具体值由式(42a)、式(43a)、式(44a)、式(44b)、式(45a)、式(45b)、式(46a)、式(47a)以及式(48a)确定.计算2 阶谱矩时,βk与 βj的具体值由相应系统系列响应变化率式(42b)、式(43b)、式(44c)、式(44d)、式(45c)、式(45d)、式(46b)、(47b)以及式(48b)确定.
5 算例
为了验证本文方法求解地震响应的正确性,将其和虚拟激励法对一栋10 层钢筋混凝土基础耗能隔震结构进行对比分析.基础耗能隔震结构力学模型如图1 所示,上部结构各层的层高h1,h2,···,h10=3.6 m,各层质量m1,m2,···,m10=310 t,各层的层间刚度k1,k2,···,k10=170 MN/m,结构阻尼比 ξ=0.05,结构的阻尼采用Rayleigh 阻尼,两个比例系数分别为a0=0.262和a1=0.007 2.隔震层质量mb=440 t,隔震层刚度kb=30 MN/m,隔震层阻尼比 ξb=0.1,支撑刚度kd=1.5kb.隔震层设置广义Maxwell 阻尼器,广义Maxwell 阻尼器中Maxwell 阻尼单元的个数r=2,阻尼器平衡刚度k0=1.2 MN/m,两个Maxwell 分支单元的刚度和松弛时间分别为抗震设防烈度为8 度,Ⅱ类场地,胡聿贤谱中低频截止频率ωc=2 rad/s,根据文献[30],胡聿贤谱激励的其他参数为:场地频率 ωg=15.71 rad/s,场地阻尼比 ξg=0.72,功率谱强度因子S0=61.93 cm2/s3.
5.1 激励与响应功率谱验证
由式(15a)和式(15b),地面运动加速度可表示为

根据式(18)、式(21)和式(24),将地面加速度表示为Duhamel 积分形式
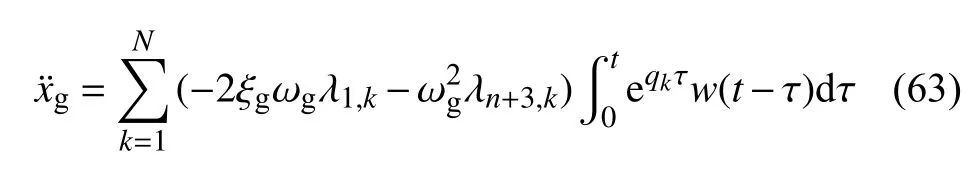
地面加速度的模态强度系数为
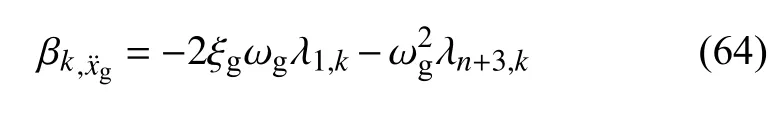
将式(64)代入式(57),得本文方法地面加速度功率谱为
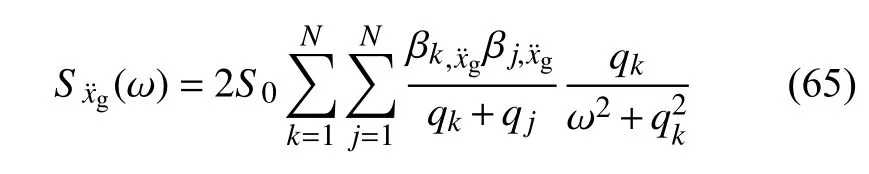
胡聿贤地震动模型的传统功率谱表达式为[13]
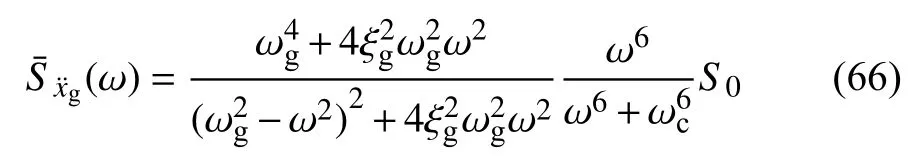
本文方法与虚拟激励法都是根据各响应功率谱求解地震响应,因此,有必要验证激励功率谱与各响应功率谱的正确性.根据式(65)和式(66),绘制本文方法和传统胡聿贤地震动模型功率谱曲线,如图3所示;根据式(57)和附录式(A16)、附录式(A17),绘制本文方法和虚拟激励法得到的各响应功率谱曲线,如图4~图11 所示.

图3 地面加速度功率谱Fig.3 Power spectrum of ground acceleration
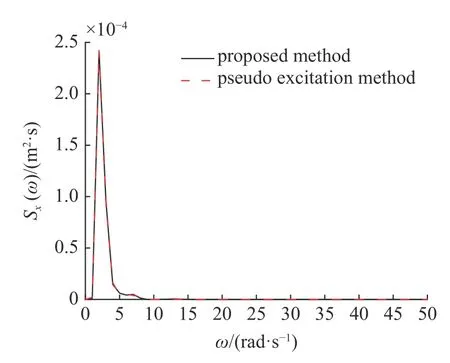
图4 第 5 层绝对位移功率谱Fig.4 Power spectrum of absolute displacement of 5th floor
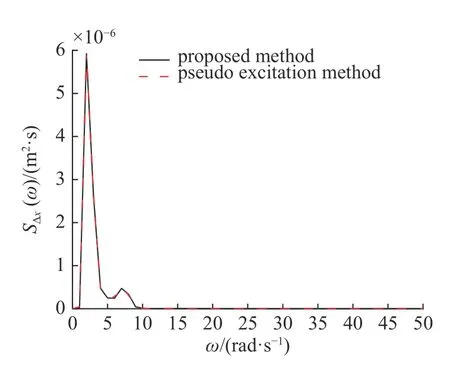
图5 第5 层层间位移功率谱Fig.5 Power spectrum of inter-storey displacement of 5th floor
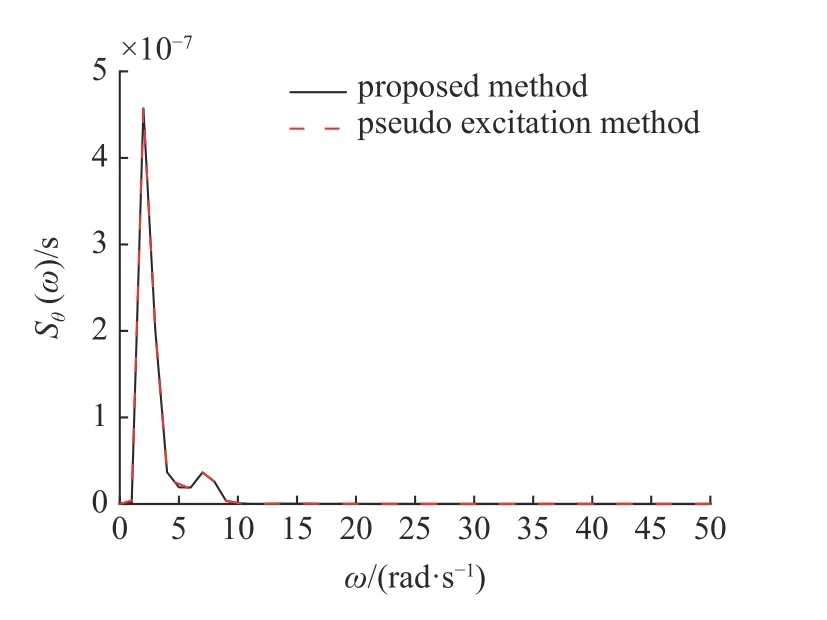
图6 第5 层层间位移角功率谱Fig.6 Power spectrum of inter-storey drift angle of 5th floor

图7 隔震层位移功率谱Fig.7 Power spectrum of isolated displacement
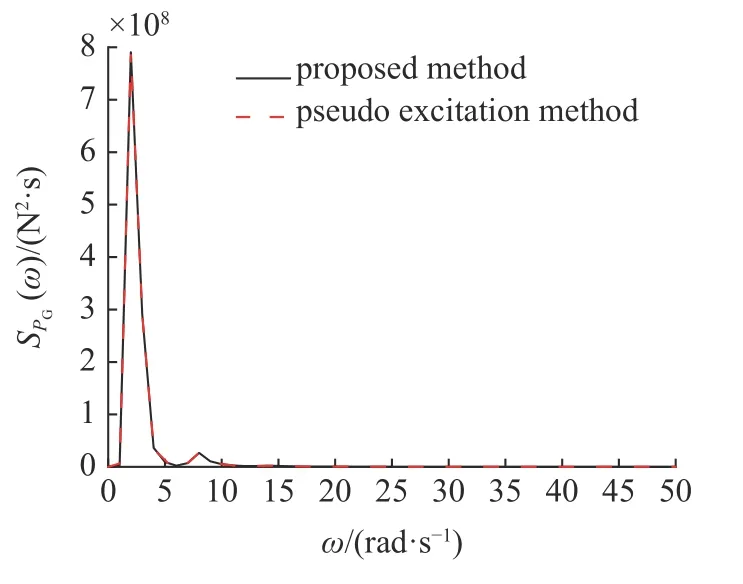
图8 阻尼力功率谱Fig.8 Power spectrum of the damping force
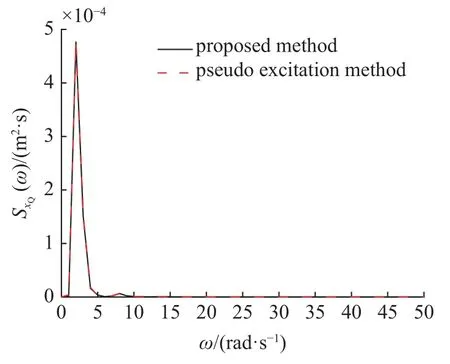
图9 阻尼器位移功率谱Fig.9 Power spectrum of damping displacement
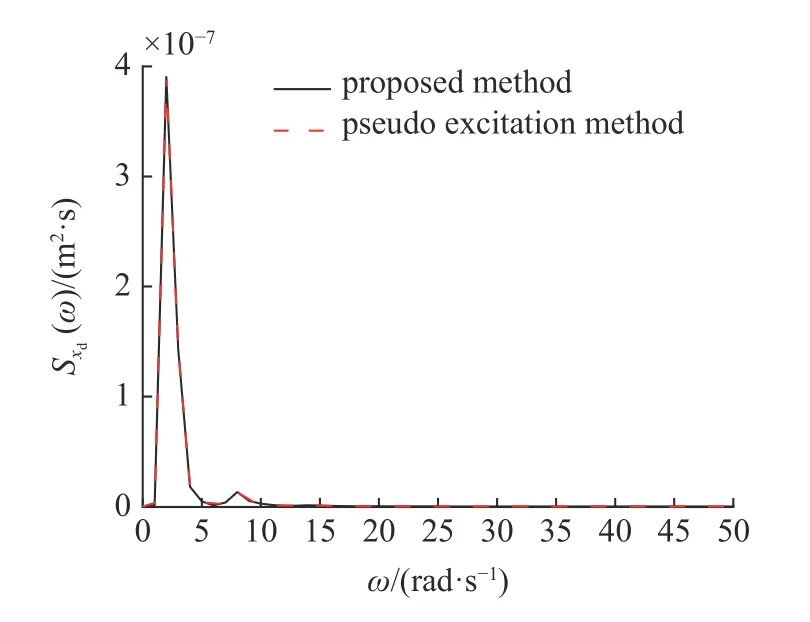
图10 支撑位移功率谱Fig.10 Power spectrum of bracing displacement
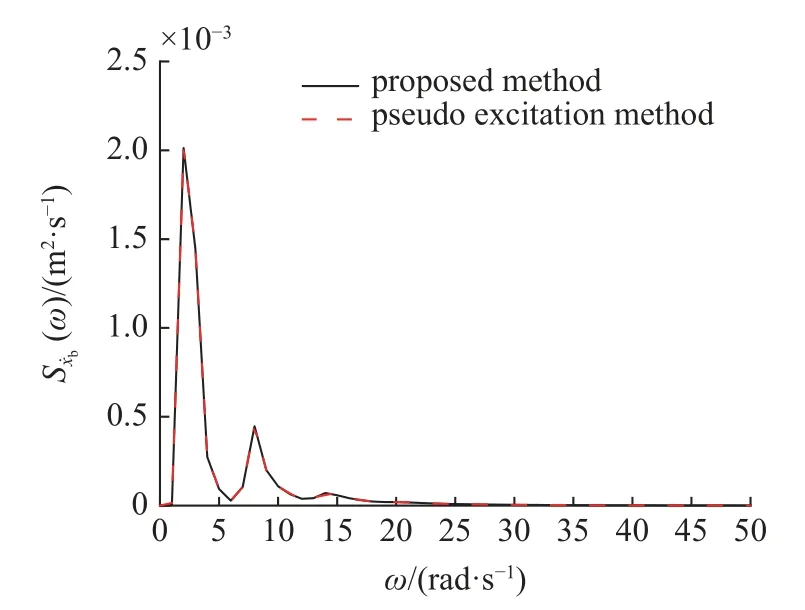
图11 隔震层速度功率谱Fig.11 Power spectrum of isolated velocity
由图3 可知,本文方法与传统表达式绘制的胡聿贤地面加速度功率谱曲线完全吻合,验证了本文方法计算地面加速度功率谱的正确性,表明通过滤波方程将胡聿贤谱激励等效转化为白噪声激励进行求解,只是物理上的转换,并不会改变地震激励的相关特性.由图4~图11 可知,本文方法与虚拟激励法绘制的系统系列响应功率谱曲线完全吻合,验证了本文方法计算系统系列响应功率谱和模态强度系数的正确性.由式(57)可知,本文所得系统系列响应功率谱表达式均为模态强度系数 βk、系统特征值qk、功率谱频域变量 ω 以及谱强度因子S0相同规律的组合,其中项为二次正交形式,功率谱的二次正交化可使系统系列响应功率谱形式保持一致,只是各响应模态强度系数不同,式(57)体现了本文功率谱表达式的简洁性,并且从功率谱表达式可直观看出功率谱强度大小和峰值随 ω 的变化情况.
5.2 谱矩计算精度和效率
为了验证本文方法计算系统系列响应0~2 阶谱矩的正确性,与虚拟激励法计算的系统系列响应0~2 阶谱矩进行对比分析.因为虚拟激励法计算谱矩是对其功率谱进行数值积分,谱矩计算精度与选择的积分步长和积分区间密切相关,积分区间越大同时积分步长越小,所得谱矩值就越精确.由系统系列响应功率谱图4~图11 可知,功率谱的卓越频率均在50 rad/s 以内,因此,将频域积分上限取为 300 rad/s,已足够高过响应功率谱的卓越频率.在积分区间[0,500]内,通过逐步缩小积分步长确定谱矩值,为提高计算结果的精度,虚拟激励法积分步长分3 种情况取值,分别为: ①Δω=0.01 rad/s ;② Δω=0.15 rad/s ;③Δω=0.25 rad/s.图12~图14 为上部结构和隔震层绝对位移的0~2 阶谱矩值,其中,隔震层谱矩值为隔震层相对于地面的谱矩值,上部结构谱矩值为上部结构相对于隔震层的谱矩值;图15~图17 为上部结构层间位移角的0~2 阶谱矩值.
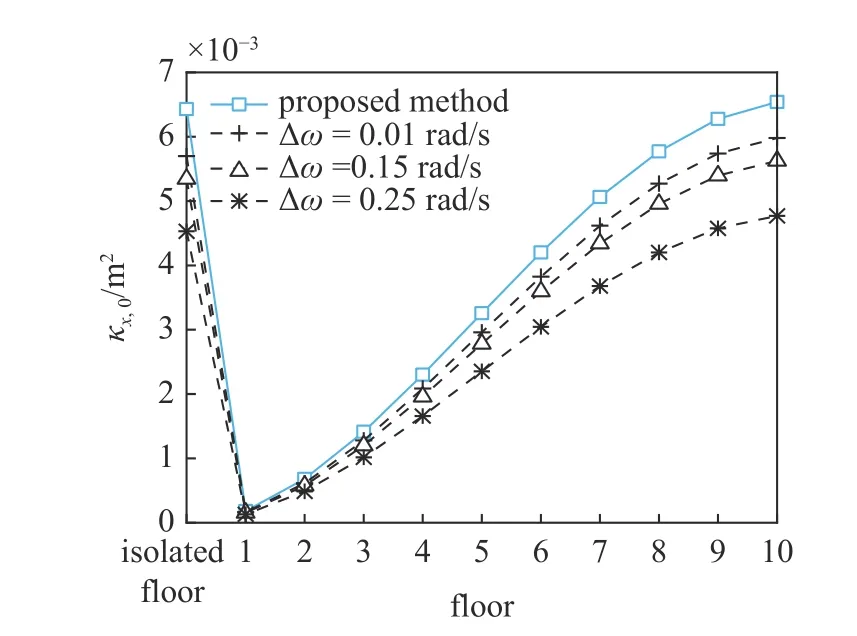
图12 结构位移0 阶谱矩Fig.12 Zero-order spectral moment of displacement
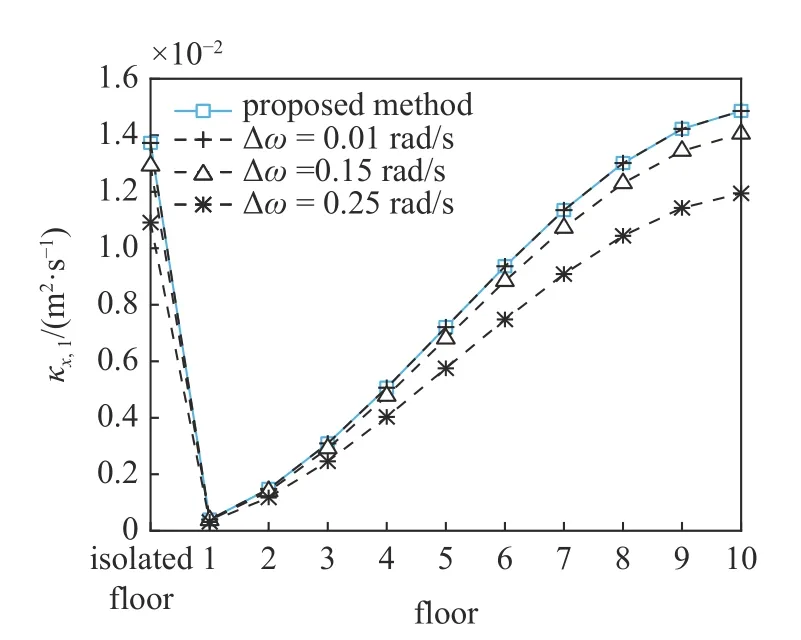
图13 结构位移1 阶谱矩Fig.13 First-order spectral moment of displacement
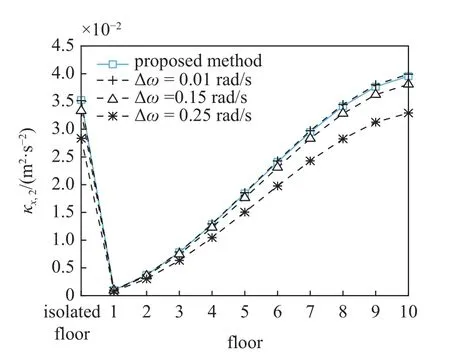
图14 结构位移2 阶谱矩Fig.14 Second-order spectral moment of displacement
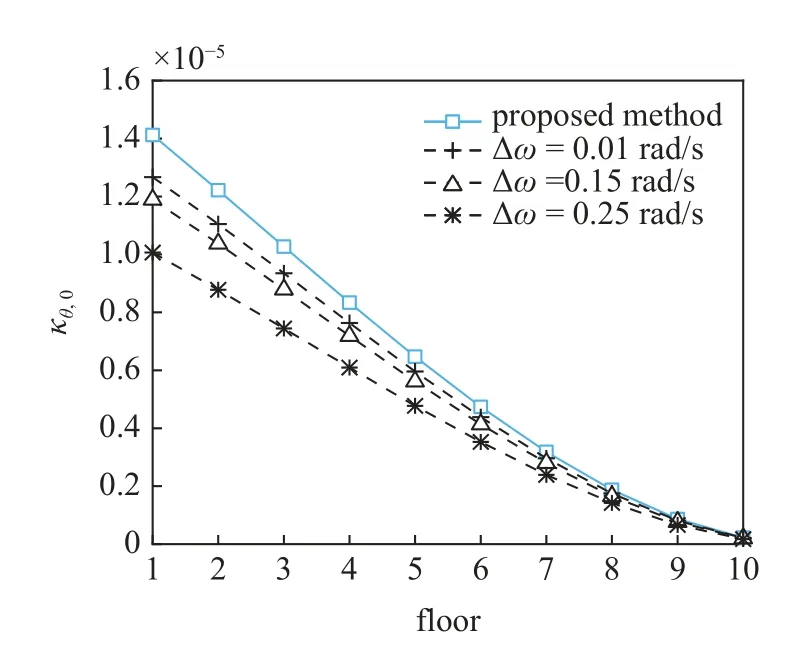
图15 层间位移角0 阶谱矩Fig.15 Zero-order spectral moment of inter-storey drift angle
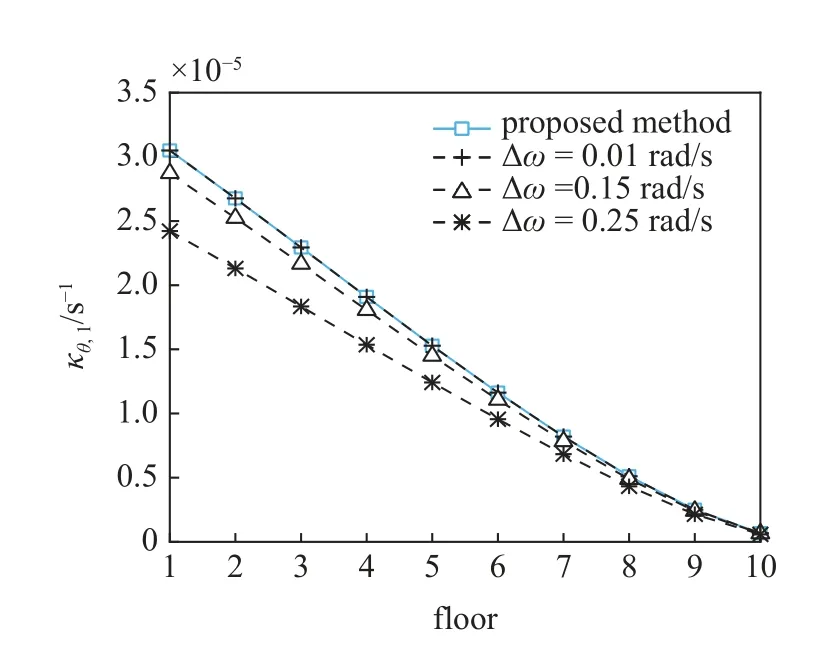
图16 层间位移角1 阶谱矩Fig.16 First-order spectral moment of inter-storey drift angle
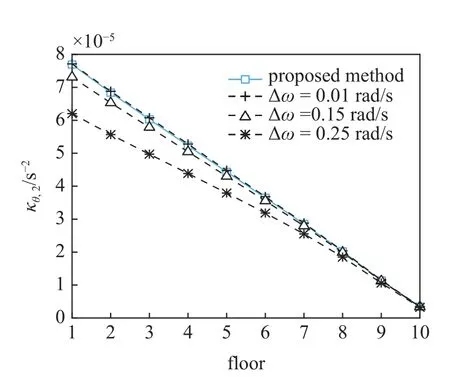
图17 层间位移角2 阶谱矩Fig.17 Second-order spectral moment of inter-storey drift angle
为了与虚拟激励法取不同积分区间的0~2 阶谱矩值进行对比,以计算阻尼器位移谱矩值为例,将频域积分步长统一取为 Δω=0.001 rad/s,通过逐步增大积分区间确定谱矩值,虚拟激励法积分区间分3 种情况取值,分别为: ④ [0,100]; ⑤[0,200];⑥ [0,300].表1 为阻尼器位移0~2 阶谱矩值,表中的误差为虚拟激励法与本文方法谱矩值的绝对误差,反映的是虚拟激励法随着积分区间的增大,所得谱矩值与本文方法谱矩值的变化情况.
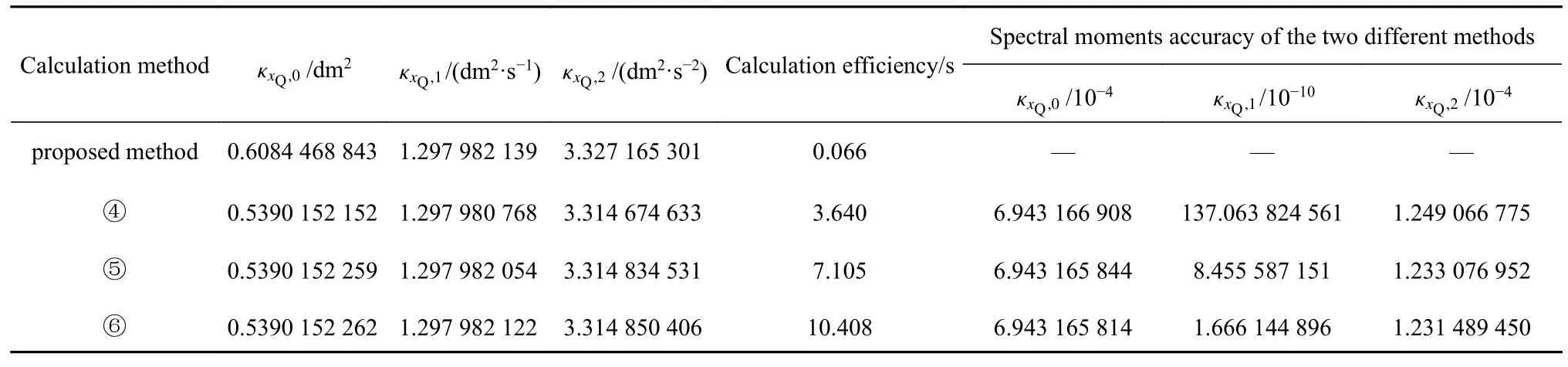
表1 阻尼器位移0~2 阶谱矩计算效率及误差Table 1 Calculation efficiency and accuracy of 0~2 spectral moments of damping displacement
由图12~图17 可知,随着频域积分步长 Δω 的减小,虚拟激励法计算得到的结构位移和层间位移角的0~2 阶谱矩值更逼近本文方法得到的谱矩值;由表1 可知,随着积分区间的增大,虚拟激励法计算得到的阻尼器位移0~2 阶谱矩值同样更逼近本文方法得到的谱矩值,这逼近的变化趋势表明了本文所得谱矩值的精确性.基于同一CPU 计算结构位移和层间位移角的0~2 阶谱矩值,本文方法一共耗时0.188 s,虚拟激励法3 种情况分别耗时: ①0.499 s,② 0.839 s,③4.305 s,虚拟激励法随着频域积分步长的减小耗时逐渐增加;由表1 可知,虚拟激励法随着频域积分区间的增大,谱矩计算精度越高,但耗时也基本成相同数量级增加,积分区间每增大 100 rad/s,耗时就增大 3 s 左右.本文方法耗时均低于虚拟激励法6 种情况耗时,由此可见,尽管本文通过复模态扩阶求解,但由于所得响应为不带积分的解析解,计算效率得到极大提高.
5.3 阻尼器减震效果
为研究随支撑刚度变化耗能系统的系列响应方差,令支撑刚度kd=rbkb,rb为支撑刚度与隔震层刚度的比值,rb按照以下6 种工况取值,分别为0.1,0.5,1.5,5,10,50.表2 为6 种工况下得到的阻尼力方差阻尼器位移方差支撑位移方差隔震层相对地面位移方差、最大层间位移角方差以及结构相对隔震层总位移方差
由表2 计算结果可知,随着rb的增大,阻尼器所提供的阻尼力和阻尼器位移增大,支撑位移、隔震层位移、最大层间位移角以及结构总位移减小,也即: 通过适当增加支撑刚度,能有效减小结构的地震响应.对于本算例,当比值rb超过1.5 时,隔震层位移、最大层间位移角和结构相对隔震层的总位移不再改变,也即: 当支撑刚度增加到一定限度时,结构的耗能减震效果基本趋于稳定.进行消能支撑结构设计时,在结构变形满足抗震规范要求的情况下,支撑刚度可以最小化以提高经济性.
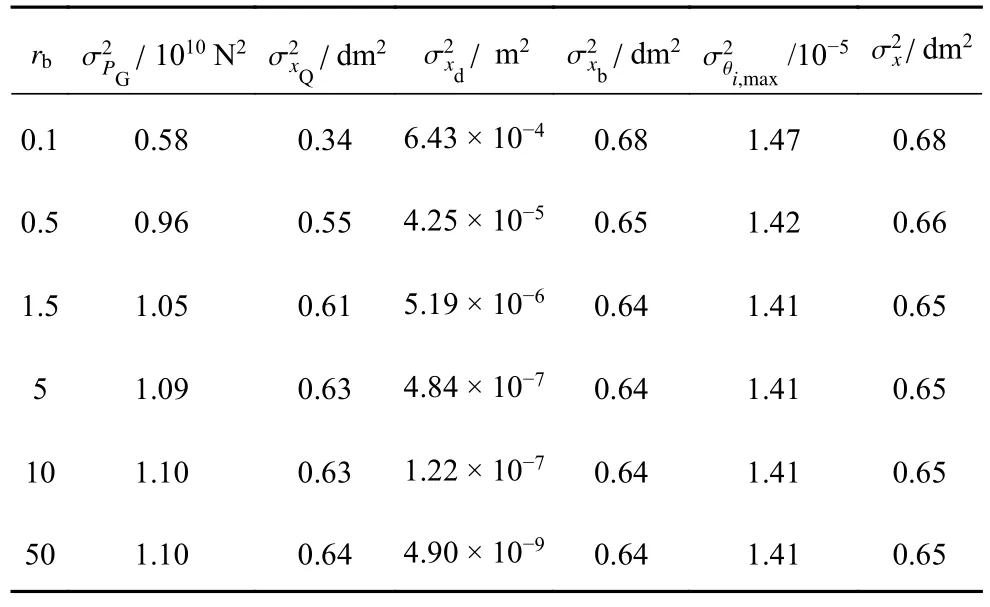
表2 系统系列响应方差Table 2 System series response variances
6 结论
本文对带支撑耗能隔震系统进行研究,以胡聿贤谱为激励做了一个完整的求解过程,为同时提高响应分析的精度与效率,提出求解带支撑耗能隔震系统随机地震响应的简明解析解法,得出以下结论.
(1)通过对比地面加速度功率谱密度函数,验证了地面激励等效转化(通过滤波方程将胡聿贤谱激励转化为白噪声激励)的正确性.
(2)本文所得谱矩解和方差解为无积分运算的解析解,对于给定相应参数,计算的0~2 阶谱矩值是精确解,虚拟激励法最精确的谱矩值和本文方法最为接近,验证了谱矩表达式的精确性,同时有显著的计算效率优势,所得谱矩解可应用于结构动力可靠度分析.
(3)支撑刚度对阻尼器减震效果有重要影响,支撑刚度越大,阻尼器减震效果越好,当支撑刚度大到一定程度时,阻尼器减震效果基本趋于稳定.
附录 耗能隔震系统的虚拟激励法
根据虚拟激励法[31],式(1)和式(2)可分别表示为
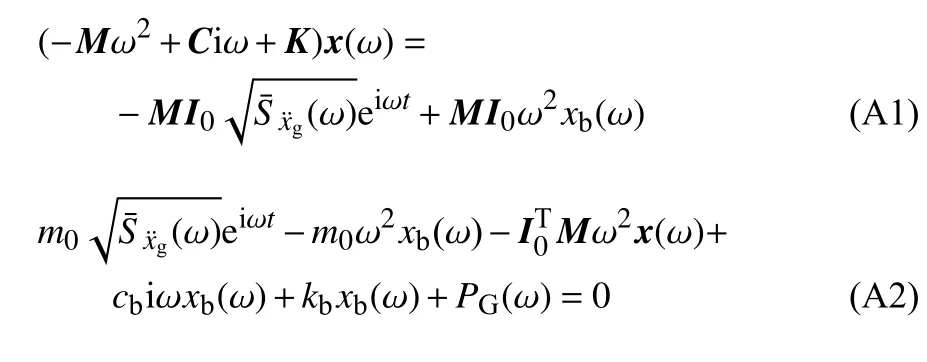
式(A1)和式(A2)中,需要求解的未知数有3 个,分别是xb(ω),x(ω) 和PG(ω).将通过等效阻尼器力的平衡关系和Maxwell 阻尼器微分本构关系,将PG(ω) 转化为用xb(ω) 表示,变换过程如式(A3)~式(A10)所示.
由式(4)和式(8)阻尼力的平衡关系,可得
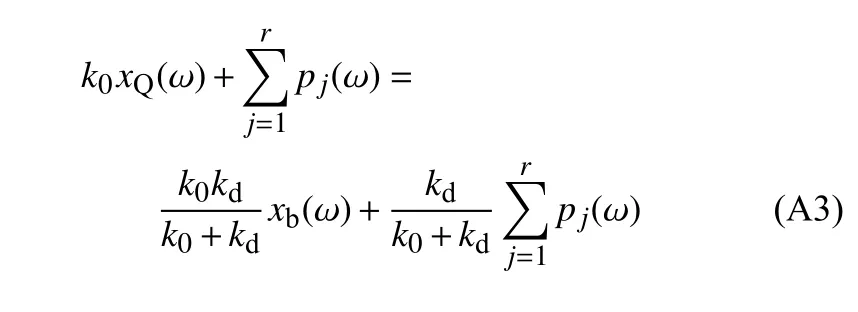
由式(11)Maxwell 阻尼微分本构关系,可得
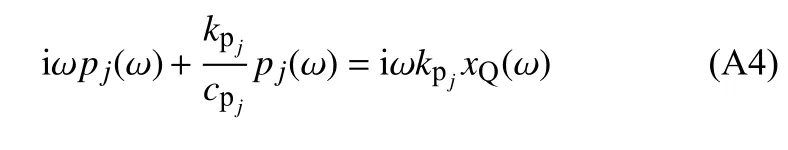
由式(A4),得p j(ω) 与xQ(ω) 的关系为
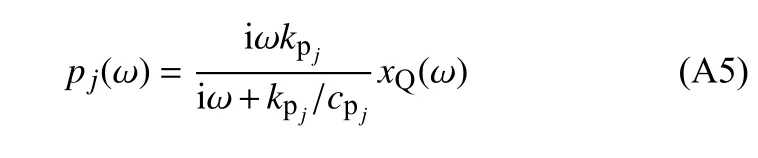
将式(A5)代入式(A3),得xb(ω) 与xQ(ω) 的关系为
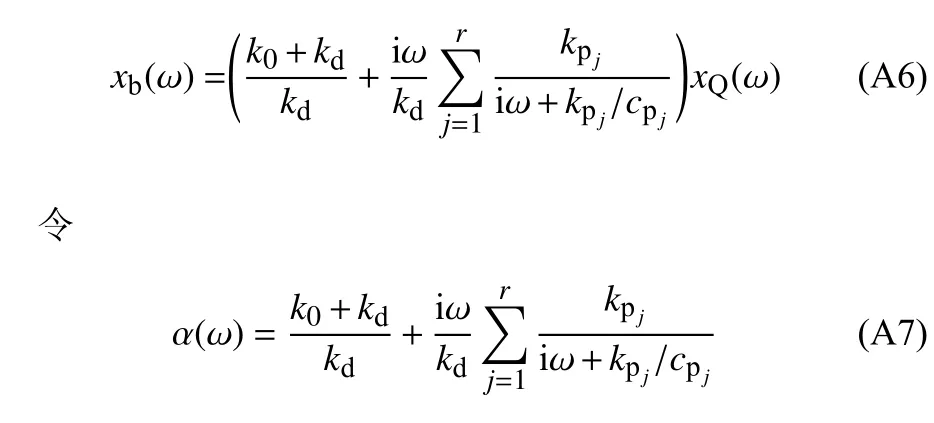
将式(A6)改写为
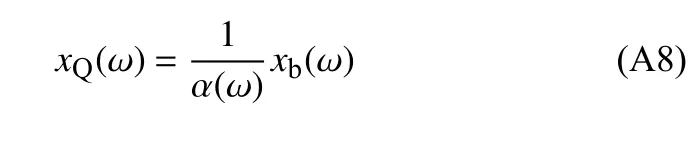
将式(A8)代入式(A5),得p j(ω) 与xb(ω) 的关系为

将式(A9)代入式(A3),得等效阻尼器受力PG(ω) 为
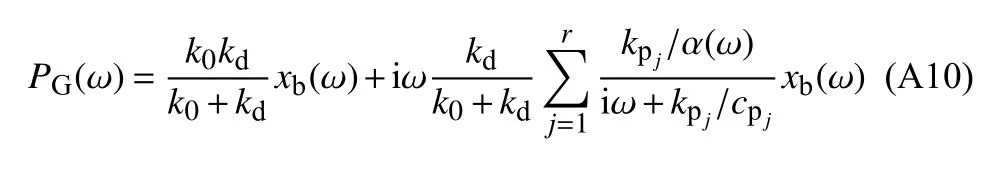
联立式(A1)、式(A2)和式(A10),即可求出xb(ω),x(ω)和PG(ω) 的频域解.
隔震层位移频域解xb(ω)为
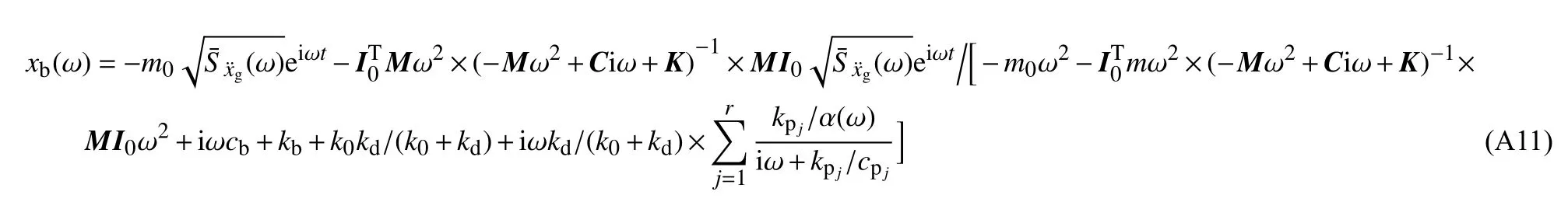
将式(A11)代入式(A8),即得阻尼器位移频域解xQ(ω)的表达式;将式(A11)代入式(A10),即得等效阻尼器受力频域解PG(ω) 的表达式.
上部结构位移频域解x(ω) 为
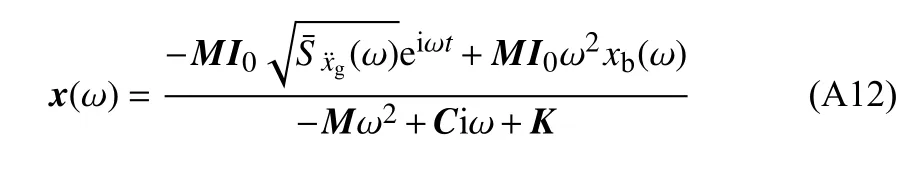
式中,xb(ω) 是已知项,其具体表达式详见式(A11).
由式(3)、式(5)和式(A10),支撑位移频域解xd(ω) 为
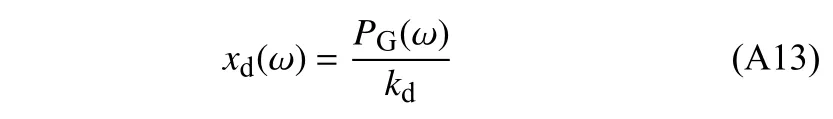
第i层的层间位移频域解 Δxi为
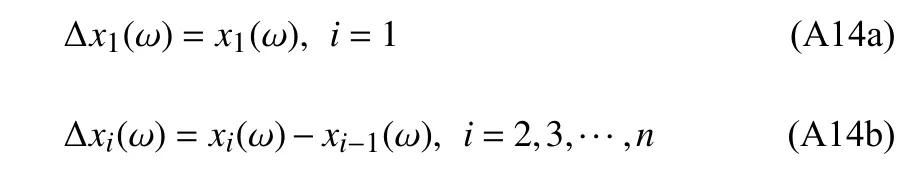
式中,xi(ω) 可由式(A12)计算得到.
第i层的层间位移角频域解 θi(ω) 为


至此,系统系列响应频域解可由式(A8)、式(A10)~式(A15) 计算得到,将频域解xQ(ω),PG(ω),xb(ω),xi(ω),xd(ω),Δxi(ω),θi(ω) 用统一符号X(ω) 表示.
系统系列响应功率谱可表示为
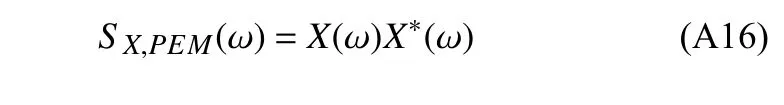
式中,X*(ω) 是X(ω) 的共轭项.
系统系列响应速度功率谱可表示为
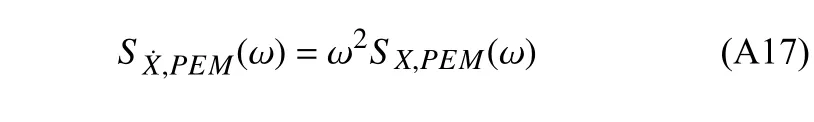
谱矩的定义如式(60)所示,对于虚拟激励法,将功率谱密度乘以 ωi并积分即可求得谱矩.将式(A16)代入式(60),系统系列响应的0~2 阶谱矩可表示为
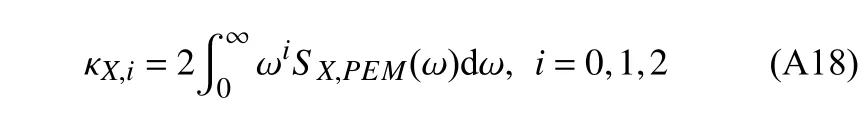
式中,i=0,1,2 分别表示系统响应的零阶、一阶和二阶谱矩.

