大型空间结构热-动力学耦合分析方法综述1)

薛明德 向志海

(清华大学航天航空学院,北京 100084)

引言

航天器中有很多可展开附件,比如太阳翼、天线、桅杆等等,这些结构大多由薄壁杆件构成.随着我国航天事业的进步,这类结构逐渐向大型化和柔性化方向发展.在轨展开之后,它们在太空失重环境中就主要受到热载荷的作用,可能产生影响结构功能的热致响应.比如准静态热变形会改变天线的形状,导致其聚焦能力下降.而本文主要关注发生在低轨航天器上的热诱发振动(thermally induced vibration)现象.因为低轨的地球半影区很窄,所以航天器只需要几秒钟就能进出地球阴影,从而使这类轻柔结构受到急剧变化的太阳热流作用.对于这类低热容和低刚度的结构,快速变化的热流会迅速改变其截面温差,并进一步激发振动响应,甚至产生不稳定的热诱发振动,即热颤振(thermal flutter)现象.

热诱发振动现象在人类早期的航天活动中就已经出现.美国的第一颗卫星Explorer I 于1958 年发射入轨后很快就发生了姿态偏转,其原因就是柔性天线的热诱发振动耗散了能量[1].加拿大于1962 年发射的第一颗卫星Alouette 1 也出现了类似的事故[2].随着航天事业的发展,热诱发振动现象也随着各种大型柔性结构的使用而陆续被观测到[3],甚至出现过热颤振现象.其中最著名的是1990 年发射的哈勃太空望远镜的柔性太阳翼弯扭耦合的热颤振事故[4],直接影响了望远镜的成像精度.后来人们只能借助航天飞机将其太阳翼更换成半刚性结构,才使望远镜能正常工作.经过多次在轨维护后,目前的哈勃太空望远镜使用的是刚性太阳翼[5].哈勃热颤振事故对国际航天工程产生了深远的影响[6],对我国相关航天器的研制也具有重要的借鉴价值.

其实在人类开展航天活动之前,Boley[7]已从理论上预测了热诱发振动现象,并引入了一个无量纲参数B来衡量发生弯曲型热诱发振动时的动态位移dmax和稳态位移dst之间的比值,即热诱发振动的剧烈程度[8]

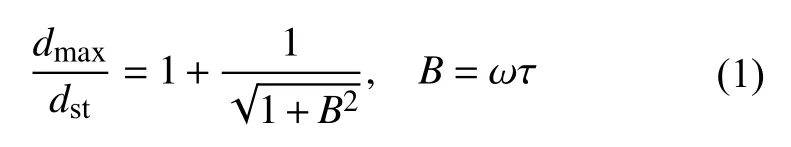
式中,ω是结构的第一阶固有振动圆频率,代表了机械振动的快慢程度;τ称为结构的热特征时间,代表了截面温差随时间变化的快慢程度.该公式简洁明了地解释了为什么轻柔结构容易出现热诱发振动.参数B也因此被称为“Boley 参数”[9].不过式(1)只适用于突加热流所产生的杆件弯曲型热诱发振动,本文的第3 节将给出复杂的空间薄壁杆系结构任意形式热诱发振动剧烈程度的度量公式,并讨论它在渐变热流作用下的准确性.

热颤振机理的研究最早见于Augusti[10]对于一根同时受到轴力和热流作用的杆模型的分析工作.他指出热颤振是一种热-对结构[11]强耦合效应所产生的自激振动现象.Donohue 和Frisch[11]也通过讨论开口薄壁杆件的扭转振动解释了OV1-10 卫星桅杆的扭转热颤振现象.Yu[12]曾试图建立悬臂杆弯曲热颤振的判断准则: 当变形前的悬臂杆指向太阳时就会发生热颤振.但Graham[13]发现Yu[12]论文中的边界条件有误,并将该热颤振准则修正为: 当变形前的悬臂杆背离太阳时就会发生热颤振.该准则也被Thornton 和Kim[4]用来解释哈勃太空望远镜的热颤振事故.不过,人们在实验中发现当热流垂直于悬臂杆入射时也会发生热颤振[3,14],并不符合Graham准则.造成理论预测和实验结果不一致的原因是: 稳定性是非线性问题,必须针对变形后的平衡状态进行分析,而Graham 热颤振准则却是基于变形前构型建立的.于是文献[15]将Graham 热颤振准则修正为: 当变形后的悬臂杆背离太阳时就会发生热颤振.本文的第4 节将对此准则进行具体的介绍,并进一步推广至复杂工程结构的热颤振分析.

明确了物理机理后,人们更关心如何分析复杂工程结构的热诱发振动和热颤振响应.由于实际航天结构大多由开口和闭口薄壁杆件构成复杂的空间杆系,需要一体地分析该复杂结构中的传热学与动力学及其互相耦合问题,这种分析工作往往需要借助于有限元程序才能开展.Mason[16]于1968 年就开始用有限元程序计算简支杆和板的热诱发振动响应.但他的有限元模型中直接采用了温度场的解析解,回避了辐射换热条件下的瞬态温度场分析这个高度非线性的难题.由于考虑辐射换热的温度计算工作量很大,用当时的计算机很难分析复杂结构的热诱发振动问题.该状况一直持续到20 世纪90 年代,特别是哈勃太空望远镜的热颤振事故之后,人们才更加重视相关的研究.Namburu 和Tamma[17]直接采用三维有限元进行热诱发振动分析,导致计算工作量非常大.为了提高计算效率,为文献[18]将闭口薄壁杆的横截面温度场分解为平均温度和摄动温度两部分,从而发展出一种谱单元来分析杆件横截面的稳态温度场,并可求出结构的准静态热变形.不过这种单元的平均温度和摄动温度相互耦合,计算工作量也不小.Thornton 和Kim[4]采用Ritz 法分析哈勃太空望远镜太阳翼的热诱发振动问题时,将薄壁圆管杆件横截面的温度场表示成平均温度加余弦摄动温度的形式,简化了热传导控制方程.而文献[19-20]进一步将任意形式(闭口或单支开口)薄壁杆件横截面的温度场展开成一般的Fourier 级数形式,发展出一种全新的一维薄壁杆件单元.该单元的每一个节点包含一个平均温度自由度和若干摄动温度自由度.利用Fourier 级数的正交性,可将瞬态热传导方程解耦为仅包含平均温度的非线性方程组和同时包含平均温度和摄动温度的线性方程组.因为有限元模型中的平均温度自由度少,因此可以很快地求解该非线性方程组,然后再高效地求解含有摄动温度自由度的线性方程组,从而提高了计算效率.另外,采用该瞬态温度单元可以与结构动力学分析的杆件单元共用节点,因此非常有利于进行热-结构的耦合分析[20-21].本文的第1 节将详细介绍Fourier 温度单元,并分析了平均温度和摄动温度时变特性的差别.本文的第2 节将介绍基于Fourier 温度单元的热诱发振动分析方法,主要强调在开口薄壁杆件、复杂结构中瞬态热传导-动力学耦合和几何非线性分析方面需要注意的问题.

到20 世纪末,国际上对热诱发振动的研究已经比较完整[22],但是分析精度尚不能完全满足蓬勃发展的太空望远镜等具有高指向精度要求的航天器的需要[6,23].近年来,NASA 还进一步开展了在轨热诱发振动实验[24],相关成果已经应用于2021 年的“双小行星重定向测试 (Double Asteroid Redirection Test,DART)”任务[25].我国的相关研究始于1997 年的国家高技术研究发展计划.和其他国家的研究相比,虽然起步很晚,但是一直立足国情致力于发展能解决复杂工程问题的高效分析方法,并在热颤振准则方面做出了有特色的工作.该研究工作断断续续地持续了二十多年,最近几年才因我国航天工程的迫切需求而引起重视,并通过地面测试验证了所发展的理论和方法[26-29],也在工程中得到了应用.在本文的后续小节中,将详细地总结这个领域的研究成果,并展望未来的工作,以期为我国航天事业的发展做一些微薄的贡献.限于篇幅,本文只强调解决这种强非线性问题(辐射换热、几何大变形、热-动力学耦合)的思路,而略去了很多具体的数学推导.有兴趣的读者请在参考文献中寻找更多的细节.

1 辐射换热下薄壁杆件的瞬态温度场分析

航天器可展附件通常包含由许多薄壁杆件组成的复杂构件.它们在太空中受到太阳和地球热流照射,同时向空间辐射散热.研究这类结构的热诱发振动问题,就必须发展高效的瞬态温度场分析算法,以及能与之协调工作的结构动力学分析算法.虽然有限元方法特别适合分析这种复杂结构,但是传统温度杆件单元的节点自由度只有平均温度,无法刻画杆件横截面内的温度分布,从而无法算出对热诱发振动至关重要的热弯矩和热双力矩.采用温度壳单元或温度实体单元虽然可以解决上述问题[17,30-31],但是需要在薄壁杆件横截面内划分很多单元,从而在求解辐射换热这种强非线性方程时会花费较多的计算工作量.另外,这些温度单元和结构单元往往不能共用一套有限元网格,不利于分析复杂工程结构的热-动力学耦合响应.针对这些问题,提出了一种Fourier 薄壁杆件温度有限单元,通过增加节点摄动温度的方法来刻画杆件横截面的温度分布,并利用Fourier 级数的正交性来提高计算效率.该温度单元可以和结构动力学分析的杆单元共用节点,因此采用一套有限元网格就可以高效而准确地计算出复杂工程结构的热诱发振动响应.

1.1 薄壁杆件温度单元[19-20]

如图1 所示,薄壁杆件单元的几何尺寸中包含轴线长度l、横截面周长Sh和壁厚ts三个尺度.由于壁厚远小于其他两个尺度,所以可以忽略温度沿壁厚的变化.于是在分析随时间t变化的温度场T时只考虑它在杆件轴线和截面周向的变化,即T=T(θ,ξ,t),其中ξ=x/l(0 ≤x≤l) 和θ=2πs/Sh(0 ≤s≤Sh) 分别是单元轴向和周向的参数坐标.

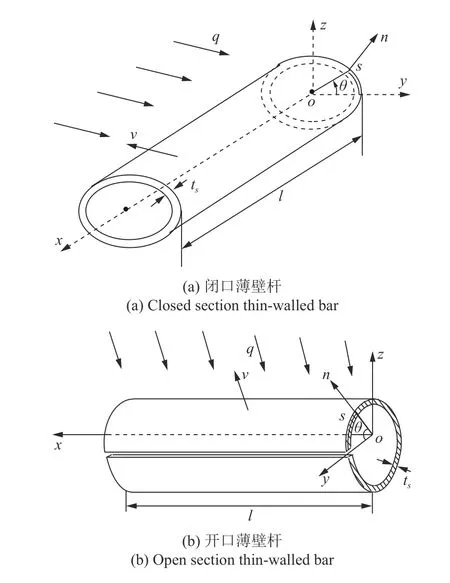
图1 薄壁杆件温度单元及其单元局部坐标系Fig.1 thin-walled bar temperature element and its local coordinate system

忽略薄壁杆件内壁的辐射换热,仅考虑其外壁向外辐射散热.根据单位长度内“体内存储的热量 +体内传导出去的热量+表面辐射出去的热量=表面吸收的热量”可在单元局部坐标系中建立控制方程

式中,c是比热容;ρ是密度;kξ和ks分别是杆件轴向和横截面周向的导热系数;αs和ε分别是杆件表面的热流吸收率和辐射率;σ=5.67×10-8W/(m2·K4)是斯蒂芬-玻尔兹曼常数;Tbk是环境背景温度.在轨环境中的太阳热流非常均匀,不沿杆件轴线发生变化(除非其他结构的遮挡产生了阴影,但分析过程并不发生实质性的改变),所以有效热流为

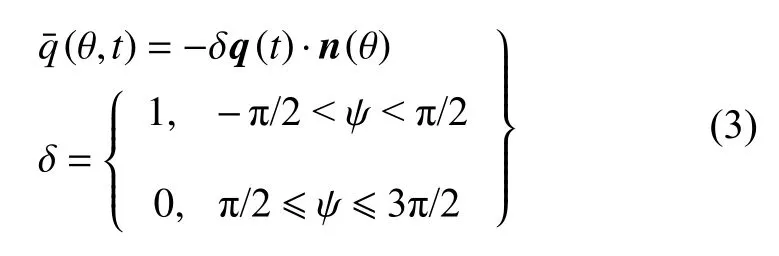
式中,n是外法线方向矢量;q=-qν 是入射热流矢量(方向矢量 ν 从杆件表面向外为正方向);吸收热流角 ψ(θ) 为 ν 和n之间的夹角,它沿薄壁杆件横截面周向的变化规律取决于杆截面形状.所以特定形状薄壁杆件所吸收的有效热流取决于各时刻入射热流q(t)与该杆件横截面各点的相对位置.

假设单元温度沿轴向线性分布,则可采用两节点Lagrange 形函数Ni(ξ) (i=1,2)在轴向插值.杆件横截面内的温度场可分解为平均温度T¯ 和摄动温度两部分,并将沿周向进行Fourier 级数展开

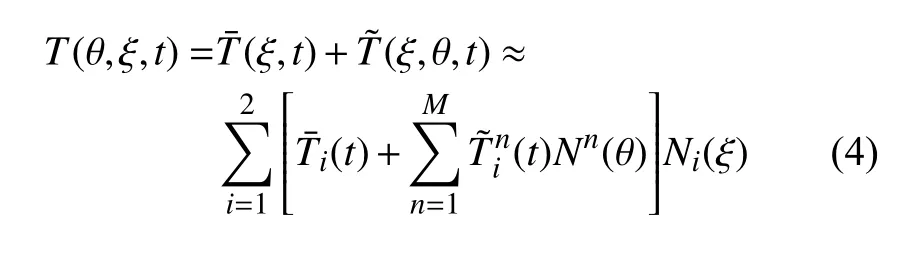
因为闭口截面的温度场在周向呈周期性分布,而开口的断面几乎为绝热边界(即 ∂T/∂θ=0),所以上式中的周向插值函数Nn(θ) 为

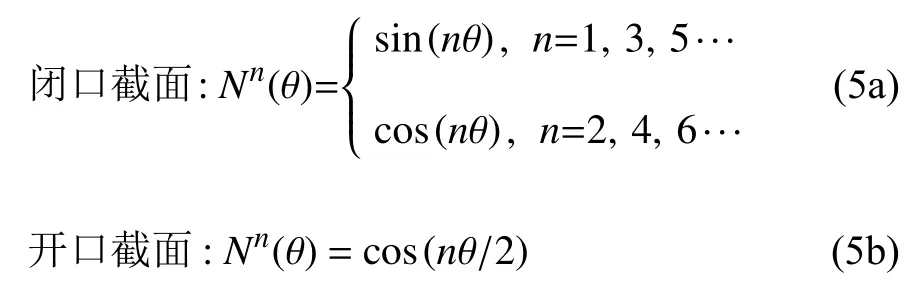
根据式(4),每个单元节点包含1 个平均温度和M个摄动温度,其中摄动温度反映了沿杆件横截面的温差.因为杆件横截面的温差(100量级)远小于其平均温度(102量级),所以方程(2)中

再注意到式(5)中的三角函数均满足正交性条件[19-21],于是可以通过方程(2)和(3)得到将平均温度和摄动温度解耦的单元有限元方程.

单元方程经过组集后[19-21]得到的整体有限元方程仍然是解耦的,其中的平均温度方程是非线性的

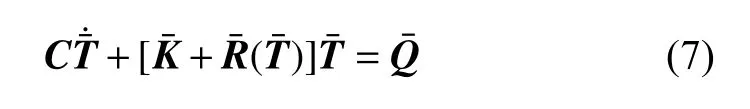
根据该方程解出平均温度后,再求解如下线性方程

就可以得到摄动温度.

基于上述理论框架,可以针对不同截面形状的薄壁杆件开发出具体的单元[32-34],甚至可以考虑入射热流被部分遮挡[33]等实际工程状况.在某些特殊的热流入射情况下,该方法还可以推广至不等壁厚的薄壁杆[34].

1.2 热特征时间

特定变形模式的热诱发振动的剧烈程度和其对应温度随时间变化的快慢相关.通常沿杆件轴线方向的入射热流分布是比较均匀的,所以只需要分析杆件横截面内的平均温度和摄动温度随时间变化的特性就能揭示热诱发振动的机理.忽略方程(2)中沿杆件轴线方向的变化项后,再注意到式(6),可以得到解耦的平均温度和摄动温度的齐次方程

上述分析表明1.1 节中利用Fourier 级数正交性得到解耦的有限单元方程的方法不仅是一种数学技巧,而且符合热传导问题的物理特性.这种方法避免了同时求解慢变量(平均温度) 和快变量(摄动温度),既保证了求解精度又提高了求解效率.具体来说,方程(7) 仅包含了少量的慢变量成分,是“浓缩”后的纯非线性部分.该方程可以用Galerkin 两点差分格式进行时间积分,在每一时间步内用Newton-Raphson 法求解.而方程(8)虽然包含了大量的快变量成分,但由于已经从方程(7)中解出,所以该方程是线性的,可以高效求解.

1.3 温度单元验证算例[33]

算例1如图2(a)所示,一根两端绝热、长度为100 mm 的闭口梯形薄壁杆受到被电池片部分遮挡的太阳热流q(1)和地球热流q(2)的照射并向外层空间辐射散热.在初始温度为290 K,环境温度为0 K 的情况下,分别用ANSYS 软件的四节点薄壳温度单元和Fourier 杆件温度单元计算其温度场.在杆件横截面周向均匀划分了21 个薄壳单元,而Fourier 杆件单元中取M=6.如图2(b)和图2(c)所示,在此复杂情况下Fourier 杆件单元和薄壳单元的计算结果非常吻合.另外,同一截面上薄壳有限元模型一共有21 个温度自由度,而Fourier 杆件有限元模型只需7 个广义温度自由度,从而减少了计算工作量.

图2 薄壁梯形杆的温度计算结果Fig.2 Temperature of a thin-walled trapezium cross-section bar

算例2如图3(a)所示,将文献[4]中哈勃太空望远镜的伸展杆由闭口圆管改为开口薄壁圆管,它受太阳热流q的照射并向外层空间辐射散热.初始温度为290 K,环境温度为0 K,分别用ANSYS 软件的薄壳温度单元(沿截面周向划分24 个单元)和Fourier杆件温度单元(M=3)计算其温度场.图3(b)和图3(c)表明Fourier 有限元的结果有足够的精度.图3(d)给出各谐摄动温度的时变历程,和图3(b)相比,可以明显地看出摄动温度的变化速度远大于平均温度的变化速度,验证了本文1.2 节的分析结果.

图3(c)显示当入射热流方向与开口薄壁杆件的几何对称面不重合时,沿杆件横截面周向温度分布不对称,因此不仅造成弯曲变形,还引起非对称的截面翘曲变形,从而产生热双力矩使杆件发生扭转.

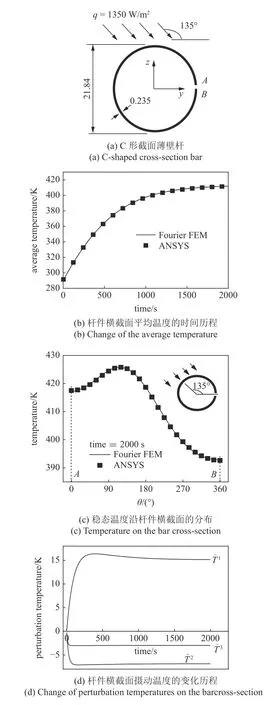
图3 薄壁C 形杆的温度计算结果Fig.3 Temperature of a thin-walled C-shaped cross-section bar

2 热-动力学耦合有限元分析

Fourier 温度杆件单元可以和常规的结构动力学杆件单元协调工作,从而便于分析热诱发振动问题.热-动力学耦合效应分为弱耦合和强耦合两种情况.弱耦合只关心瞬态温度场所产生的结构动态热变形,而强耦合还需考虑结构热变形改变了它所吸收的有效热流后对温度场造成的影响.分析热颤振问题时,必须考虑热-动力学强耦合效应[10].

柔性可展开附件的结构动力学分析应该考虑几何大变形的影响.对于刚性太阳翼等比较刚硬的结构,则完全可以采用线性方法进行分析.

2.1 热-动力学耦合有限元分析的一般框架

最一般的情况,需同时考虑辐射换热、几何非线性和热-动力学强耦合三种非线性问题.此时应采用迭代法逐步求解[20-21,33].如图4 示,设t时刻的所有场变量都为已知,则可在全局坐标系(X,Y,Z)中求解t+Δt时刻的节点温度t+ΔtTg和节点位移t+Δtug.

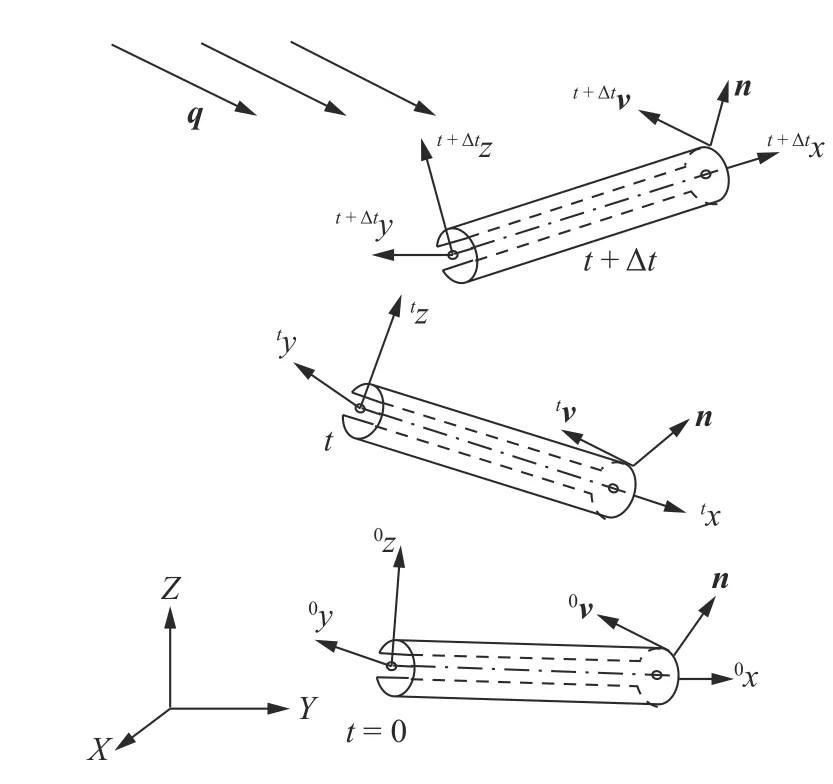
图4 杆单元的变形过程Fig.4 Deformation of the bar element

首先用第1 节的方法求解t+ΔtTg.为表述方便,可认为是求解方程(7)和(8)的合并形式

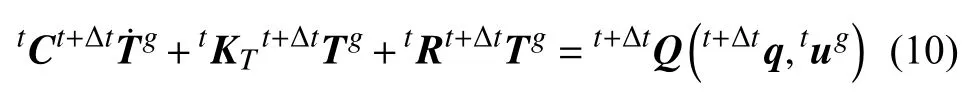
上式中的热流载荷向量是先在t时刻单元局部坐标系(tx,ty,tz)中根据式(3)计算,然后再转换到全局坐标系(X,Y,Z)中的.

在假设薄壁杆件的横截面是刚周边的前提下,定义在单元局部坐标系中的杆件外表面法向矢量n沿杆件横截面周向的分布只和杆件横截面形状有关[37-38],不随杆件变形而改变.但是,由于太阳热流方向是恒定的,定义在单元局部坐标系中的入射热流方向矢量tν 将随着杆件的变形tug而改变(具体可见2.2 节).

根据t+ΔtTg可计算结构所受的热载荷向量t+ΔtF(包括了由平均温度产生的热轴力,摄动温度产生的热弯矩和热双力矩),然后通过如下更新拉格朗日格式的非线性动力学方程求解t+Δtug

其中,t f是内力向量;tM和t D分别是质量矩阵和阻尼矩阵.由于热诱发振动是典型的小应变大转动问题,所以就是常规的线弹性刚度矩阵.而几何刚度矩阵包含了初应力的贡献,也考虑了温度变化的影响.方程(11)可用Newmark 法进行时间积分,并在每一时间步内用Newton-Raphson 法迭代求解.

结构变形后其所受热流会发生变化,从而导致温度改变,并进一步影响热变形.这种热-变形的强耦合效应在热传导方程(10)中体现为t+ΔtQ和位移tug相关,动力学方程(11)中t+ΔtF和温度t+ΔtTg相关.为保证解的正确性,需要迭代求解方程(10)和(11),直至t+ΔtQ的变化量小于预设值.迭代过程中,这些方程中的矩阵和向量都需要根据构型的变化进行更新.

在求解过程中还需要注意以下几个问题.

(1) Newton-Raphson 法的切线预测步骤所用的斜率是比较灵活的,所以在KNL中只考虑杆件轴力引起的非线性效应即已体现关键物理特征[33].

(2) Newton-Raphson 法的路径修正步骤需要正确地计算不平衡力.若直接用积分方法计算内力向量,会因构型转换而非常繁琐.而根据刚体转动准则[39],考虑到Cauchy 应力在随体坐标系下不会因为刚体转动而改变,就可以直接将k-1 构型单元局部坐标系中的内力k-1fe(而不需要转换到k构型)加上表达在k构型局部坐标系中的增量内力 Δfe,得到k构型单元局部坐标系中的内力

(3) 对于开口薄壁杆需要考虑截面翘曲位移所产生的约束扭转效应,以及杆件横截面形心和扭心之间的坐标转换关系[33-34,40-41].

(4) 应采用2.2 节介绍的Rodrigues 公式来描述杆单元的空间大转动关系,以保证求解精度.

2.2 大转动情况下的构型转换关系[33]

方程(10)和(11)中的矩阵和向量是首先在某个构型的单元局部坐标系中建立后,再转换到全局坐标系(X,Y,Z)中的.这些坐标转换会直接影响求解精度,特别是热-变形强耦合分析的准确性.

如图4 所示,以位移为例,因为初始构型单元局部坐标系(0x,0y,0z)是已知的,所以可以用常规的坐标转换矩阵将初始构型中的向量0ue表达为全局坐标系(X,Y,Z)中的向量0ug

将初始构型的单元局部坐标系(0x,0y,0z)进行刚体转动后就可以得到t时刻构型的单元局部坐标系(tx,ty,tz),从而可以用相应的正交矩阵建立0ue和tue之间的关系.但是对于热诱发振动这种小应变大转动问题,若用Euler 转动公式来计算(tx,ty,tz)不但失去了保内积的性质,而且所得结果还依赖于绕坐标轴的转动顺序,因此必须使用精确的正交矩阵进行计算.如图5 所示,此时认为(0x,0y,0z)是先绕正交矩阵的轴方向矢量teβ旋转tβ 角度到达(tx,坐标系后,再绕tx轴旋转tγ 角度到达t时刻单元局部坐标系(tx,ty,tz).相应的转换关系为

图5 杆单元的构型转换Fig.5 Configuration change of the bar element

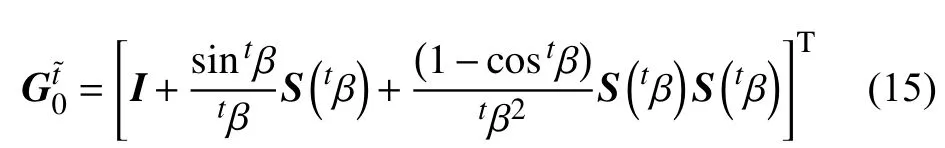
式(15)是精确的,和绕坐标轴的转动顺序无关.当tβ 很小时,式(15)就退化为Euler 转动公式.根据式(13)和式(14),就可以实现在全局坐标系和任意时刻单元局部坐标系之间的转换.

2.3 热-动力学强耦合算例[21,34]

采用上述全耦合方法分析图6 所示哈勃太空望远镜的热颤振事故.文献[4]所建立的传热学和力学模型是闭口薄壁圆杆,只能模拟热诱发弯曲振动现象,无法回答“热为什么会引起扭转振动”的问题.实际上该太阳翼的Bi-Stem 支承梁是开口薄壁杆件,在轨展开后其开口方向是随机的.为了更加接近这种实际情况,在有限元模型[24,40-41]中采用开口C 型圆杆来模拟支承梁,并假设左右梁的开口方向有θ=20°的偏差.太阳翼中部的柔性太阳毯采用等效的闭口薄壁圆杆单元网格模拟.模型中还考虑了在轨展开后太阳毯受到的29.5 N 的预张力,以及左右梁受到的14.75 N 预压力.模拟时取太阳热流为1350 W/m2,沿 ψ=80°角入射.

图6 哈勃太空望远镜太阳翼模型Fig.6 The model of the HST solar array

从图7 可以看出,热诱发振动包含了弯曲(0.097 Hz)与扭转(0.004 0 Hz)两种不同模式的振动.大约在1200 s 时太阳翼开始失稳,此时梁的压缩轴力达到了压杆失稳的临界值.图7(c)显示的失稳后的弯扭耦合变形图和实际照片非常相似.由此证明了本文方法的有效性.图7(a)还说明,虽然采用线性分析可以模拟出弯扭耦合热诱发振动,但是无法得到热颤振和热屈曲的正确结果.可见对于柔性大型空间结构,必须采用非线性分析.

图7 哈勃太空望远镜太阳翼的模拟结果Fig.7 The simulation results of the HST solar array

3 产生热诱发振动的必要条件

式(1)只适用于评价突加热流作用下纯弯曲梁的热诱发振动剧烈程度.而实际工程结构的振动模式是非常复杂的,所受热流也不是理想的阶跃函数.故需讨论一般情况下产生热诱发振动的必要条件.

3.1 理论分析[37]

为了能得到类似于式(1)的解析定量结果,本节和Boley[7-8]原始论文一样,只采用线性结构模型且不考虑热-结构强耦合效应.为得到一般的结果,采用了有限元模型进行分析,此时方程(13)退化为

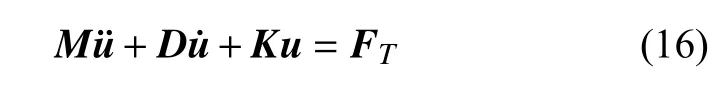
式中的刚度矩阵K可以包含预应力.热载荷FT包含了热轴力、热弯矩和热双力矩.其中热轴力和杆件横截面平均温度有关,是慢变量;其他和杆件横截面的摄动温度有关,是快变量,可能导致热诱发振动.为评估产生热诱发振动的必要条件及剧烈程度,用模态叠加法求解由摄动温度引起的位移[37].

记为产生的热诱发振动位移,它在振动模态空间表达为分别是系统的第i阶振动模态和模态坐标.将热载荷转换至振动模态空间,于是方程(16)可以解耦为I个独立的方程

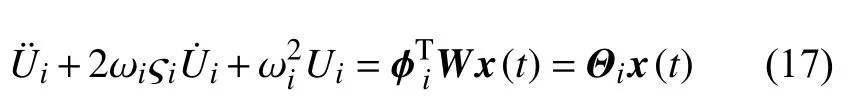
式中,ωi和 ςi分别为系统的第i阶(i=1,2,···,I)振动圆频率和阻尼比,而 Θix(t) 可以表示为

于是可知在突加恒定热流并忽略阻尼的条件下,第i阶模态热诱发振动的剧烈程度为

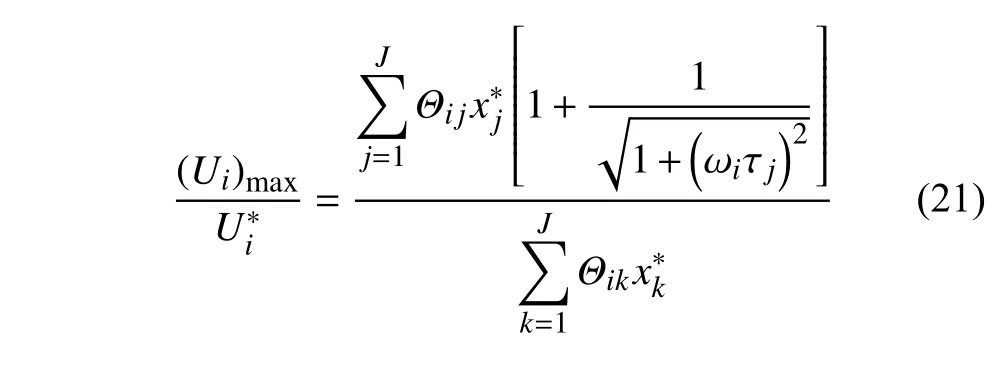
上式说明第i阶模态热诱发振动的剧烈程度不但和 ωi有关,而且和各阶热特征时间 τj都有关.若只考虑第一阶热特征模态(J=1),则式(21)退化为式(1).式(21)对具有复杂模态的工程结构仍成立,而Boley[6-7]所给出的热诱发梁弯曲振动只是一特例.

式(21)成立的条件也是非常理想的.实际结构中会存在阻尼,可能是非线性的,所受热流也不是理想的阶跃函数.此时式(21)的估计往往是保守的.

3.2 算例说明

算例1文献[4]将哈勃太空望远镜太阳翼的Bi-Stem 梁(见图6)简化为闭口薄壁圆管,给出了其热诱发振动的理论估计.文献[43]改变帆板伸展梁的厚度和传热参数,用本文数值解得到不同的Boley参数与帆板端部最大位移占准静态位移之百分比的关系(见图8),和理论预测非常吻合.

图8 杆端部的热诱发振动剧烈程度随B 的变化Fig.8 The bar tip TIV intensity changes with B

算例2图9 是一个典型的半刚性太阳翼力学模型,主要由受18.9 N 预张力的张紧网、受预压力的支承梁、顶板以及边框等组成.整个结构由10 块太阳能帆板展开而成,每块帆板分为4 个700 mm ×750 mm 框.帆板框由薄壁正方形管构成,支承梁为薄壁圆管.帆板框和支承梁固结于卫星舱体上.有限元分析时将电池片质量计入由凯夫拉纤维构成的张紧网纤维上,略去舱体运动对帆板的影响并假设二者之间绝热.从0 时刻开始,结构受到垂直于帆板平面的太阳热流照射,并向太空辐射散热.太阳翼各构件的尺寸和材料见表1.

图9 突加热流作用下的半刚性太阳翼Fig.9 A semi-stiff solar panel subjected to suddenly applied heat flux

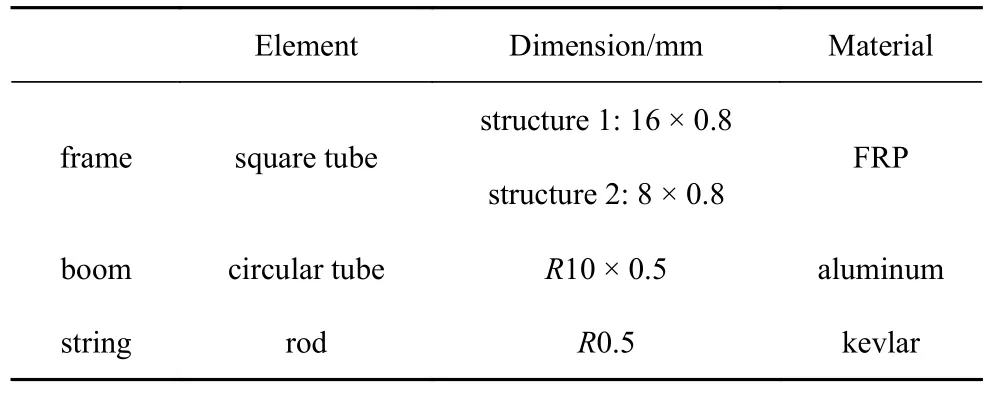
表1 太阳能帆板各构件的尺寸及其材料Table 1 Dimension and material of the solar panel

文献[43]采用杆件Fourier 有限元对该太阳翼模型进行离散,总计682 个节点,1052 个单元.其中支承梁采用薄壁圆管单元,张紧网绷弦采用实心圆杆单元(其材料参数已经等效了电池片的质量和热容量),帆板框和顶板为薄壁矩形管单元.分别用直接积分法和基于Lanczos 方法的模态叠加法计算温度场,所得摄动温度吻合得很好(见图10).用Lanczos 方法得到结构1 边框的热特征时间为10.47 s,而对摄动温度时程曲线以指数函数拟合得到的热特征时间约为10.5 s,二者一致.

图10 帆板框(结构1)和支承杆的摄动温度时间历程Fig.10 Change of perturbation temperatures of the frame and boom

图11 是采用弱耦合方法得到的A点(见图9)热诱发振动响应.其中的结构1 和结构2 可见表1.表2 显示,对于这个比较复杂的结构实际的热诱发振动剧烈程度比式(1)的估计低.这是因为该结构的第一阶模态不是理想的纯弯曲梁形式(帆板是板振动模式,和支承梁的弯曲模式不同),热特征时间也不能完全由边框代表.

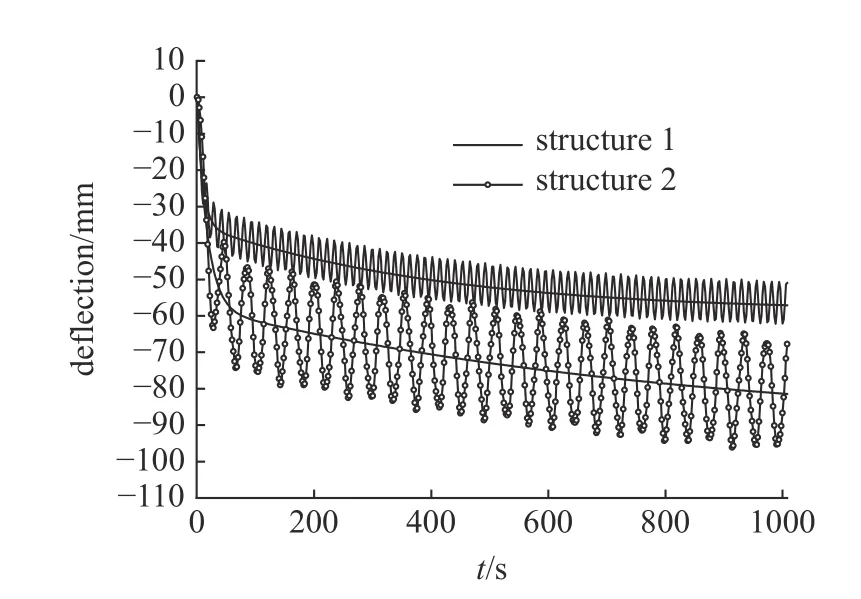
图11 突加热流作用下太阳翼端部的法向位移Fig.11 Tip displacement of the solar panel subjected to suddenly applied heat flux

表2 A 点的主要特征量 (t=2000 s)Table 2 Main features of point A at t=2000 s

算例3实际的入射热流总是经过一段时间后才逐渐稳定的,不可能是阶跃函数.因此经典的热特征时间总是小于实际温差趋于稳定的时间,热诱发振动的剧烈程度也会小于式(1)或式(21)的估计值.比如,在轨航天器在进出地球阴影时,总会经过一段半影区,轨道越高半影区越宽,热流变化越慢,越不容易产生热诱发振动[3].另外,柔性结构由于发生了大转动,吸收的热流会比只发生小转动的刚性结构少一些,热诱发振动也会小一些(没发生热颤振时).文献[28]根据1.5 m 长和2 m 长之柔性悬臂梁的热诱发振动试验的测量数据,进一步讨论了这些因素,并根据温差变化情况拟合出等效的热特征时间τeff和相应的等效Boley 参数Beff=ω1τeff.从图12 的比较结果来看,经典理论预测的热诱发振动最剧烈,等效理论的预测结果和实测结果接近.

图12 经典理论、等效和实测振动比的比较[28]Fig.12 Comparison among the original,effective and actual ratio of dmax/ dst[28]

4 热诱发振动的稳定性

热诱发振动发生不稳定的物理机制是结构振动变形使结构所吸收的有效热流q¯ 因结构振动变形而震荡变化(见式(3)),从而产生热-结构系统的运动稳定性问题.稳定性是系统略微偏离平衡状态后表现出的性质,所以应该在结构变形之后的构型上进行讨论.另外,结构发生失稳说明产生了不唯一的解,意味着这一定是非线性问题.但根据里雅普诺夫关于运动稳定性问题的一次近似判别准则[44],可用系统方程在变形之后构型的一阶Taylor 展开项的性质来判别是否失稳.本节先借助悬臂杆件热颤振这个简单问题说明研究热颤振的基本方法,然后再将它推广至复杂的工程结构.

4.1 悬臂梁热颤振准则

以图13 所示模型来解释引言中介绍的热颤振准则.以半径为R的闭口薄壁圆管为例,根据第1 节的理论可得到解耦的平均温度和一阶摄动温度的控制方程

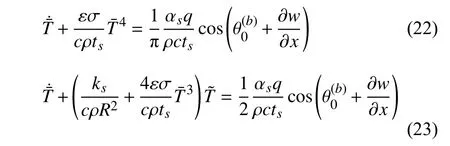
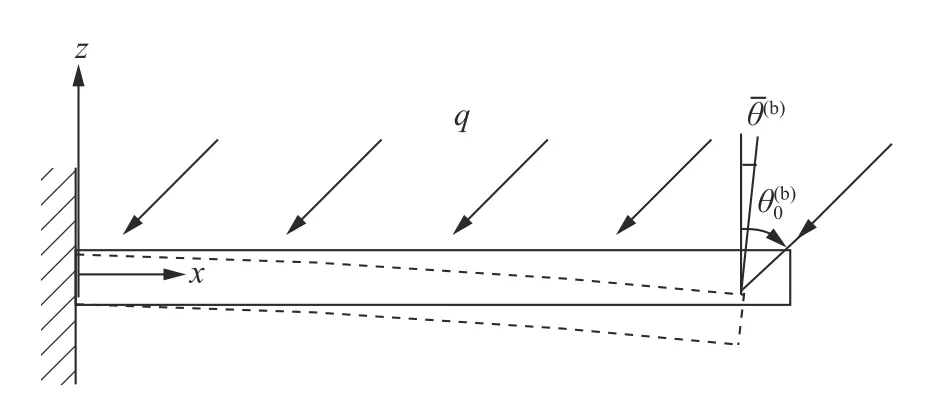
图13 悬臂梁受突加热流作用Fig.13 A cantilever beam subjected to suddenly applied thermal flux

对无阻尼的悬臂杆,令z方向位移w的插值形式为w(x,t)=N(x)W(t),方程(16)变为

采用同样的思路,也可以得到太阳帆的热颤振条件[45],甚至在考虑开口方向的影响后还可以进一步得到开口杆件的热颤振准则[34,46].

4.2 热颤振的能量解释

发生热诱发振动时,入射热流的方向ν并未改变,所以这是一种典型的自激振动.当系统从外界吸收的热量超过发散的热量时,就会发生热颤振.因此,也可以从能量的角度推导出悬臂梁的热颤振准则[29,47].

围绕着稳态平衡位置,梁的转角是振荡的θ(b)(t)≈相应的法向有效热流为

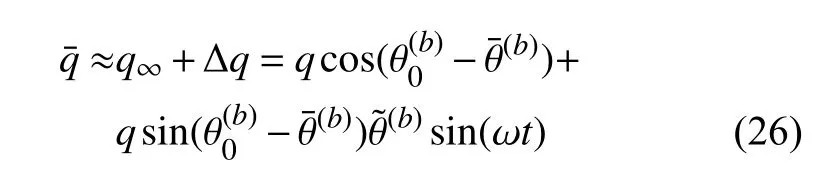
将式(26)代入式(23)并注意到ks/R2≫4εσT¯3/ts,可得

一个周期T=2π/ω 内,热弯矩做的功为

4.3 复杂结构的热颤振分析[38]

对复杂工程结构可先计算其低阶固有频率和对应的热特征时间,按照第3 节“发生热诱发振动的必要条件”,初步判断是否会发生热诱发振动.

对于柔性结构,需按第2 节,计算结构振动随时间的变化,判断会否发生热诱发振动与热颤振.

若结构刚度较大,可按有限元方程直接分析热诱发振动的稳定性区间[34].将式(17)写成矩阵形式

并在式(8)中考虑振动耦合项BIU的影响

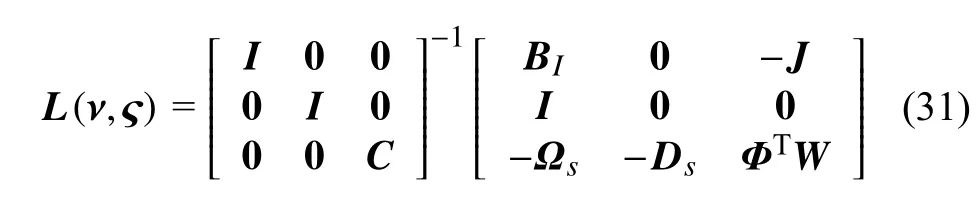
式中,J为相对于稳态的一阶近似;ν为入射热流的方向矢量; ς 为阻尼比向量.

根据常微分方程理论,当矩阵L(ν,ς)的最大特征值的实部α＜ 0 时,系统是稳定的;当α＞ 0,则系统不稳定;当α=0,则系统处于临界状态.

现以一个典型的环形天线(见图14)在突加太阳热流作用下的稳定性分析[38,48]来说明本文方法的实际应用.环形天线由主杆、圈杆、竖杆和上下反射网构成,其截面尺寸以及材料见表3.天线各构件都采用薄壁圆管单元模拟,总计748 个单元.假设天线通过主梁固结于卫星舱体,并忽略与卫星之间的传热,只研究环形天线本身的热-动力学问题.

表3 环状天线的单元类型,尺寸与材料Table 3 Dimension and material of the circular antenna

该天线系统的稳定性取决于三个参数: 入射热流矢量的方位角φ1和φ2和系统阻尼系数ς.根据式(35)矩阵的最大特征值实部α(φ1,φ2,ς)=0 的条件,可解得临界曲面,它将三维参数空间划分为稳定区和不稳定区(见图15).

利用图15 所给分区,分别在稳定区、临界面和不稳定区计算环形天线的热诱发振动响应,可进一步验证本节运动稳定性分析的可靠性.图16 是在给定热流方向时阻尼比和α的关系.可见阻尼小于临界值ςcr后系统就不稳定,此结论也可通过图17 中A点(见图14)的Z向振动情况得到印证.

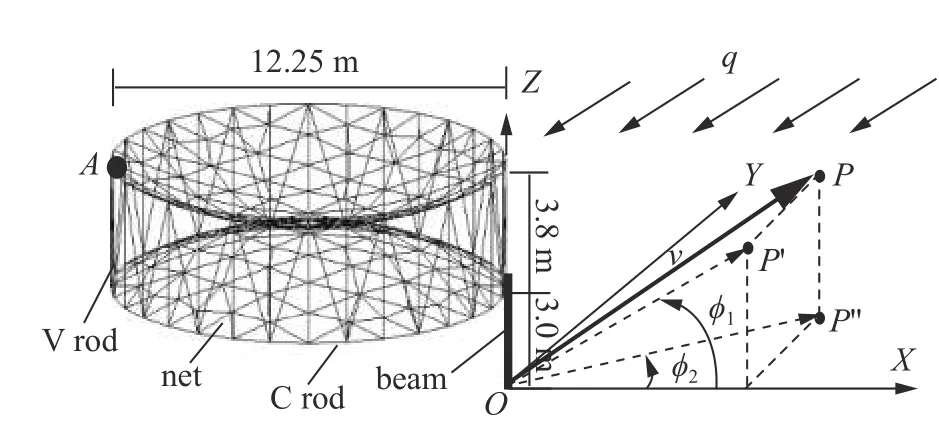
图14 突加太阳热流作用下的环状天线Fig.14 Circular antenna under the incident heat flux

图15 环状天线的稳定性边界Fig.15 Stability boundary of the circular antenna

图16 α 的根轨迹图Fig.16 The locus of α

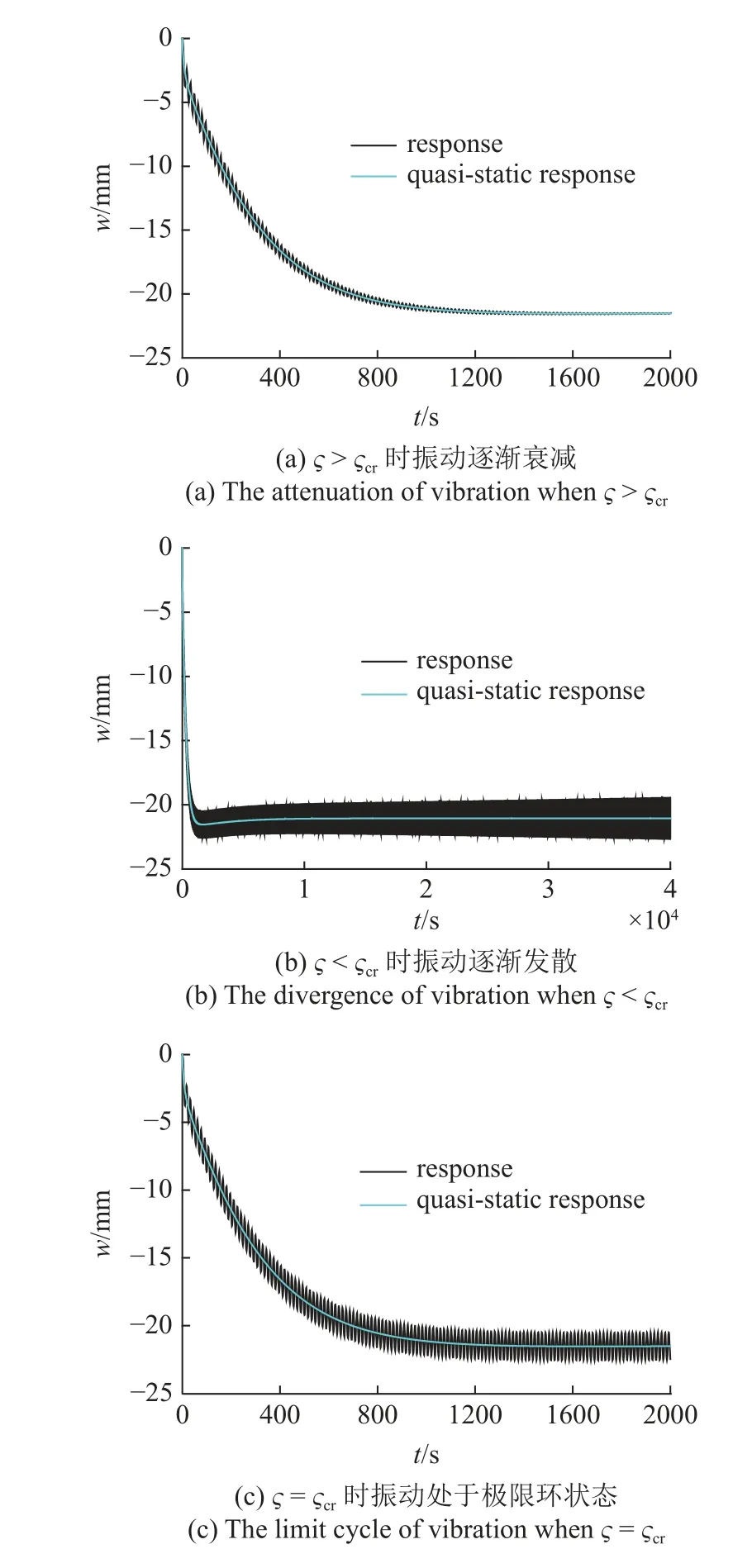
图17 A 点Z 向振动Fig.17 The vibration in Z direction at point A

5 其他实际问题

前文已经将热诱发振动和热颤振的机理、特性和分析方法做了详细的介绍,其关键在于理解慢变量和快变量性质,并采取相应的应对措施.本节将进一步讨论分析复杂工程结构时需要注意的问题.

工程结构往往由很多不同种类的构件组成.对于不同截面形式的杆状构件,需要用不同的Fourier杆件温度单元.另外,还有一些构件不是杆状的,比如太阳翼的电池板.为了能和Fourier 杆单元配合使用,可以采用等效的梁格模型[34,49],即用Fourier 杆单元网格来等效电池板.此时不但要求所有力学特性(比如频率)等效,还要求热学特性(比如热特征时间)等效.

现代航天器的可展开结构不断向大型化和柔性化方向发展.当它们的转动惯量和航天器舱体相比不再是一个小量时,就必须考虑和舱体的耦合动力学问题[38,49].此时可以采用强耦合方式进行分析.但稳定性分析的结果表明,空间结构和航天器舱体的转动惯量比越大,系统越容易失稳,此时需要再考虑和姿态控制系统的协调关系[44].

工程中还特别关心怎样避免产生热诱发振动,或者怎样抑制热诱发振动.由于热诱发振动的频率很低(通常在0.1 Hz 左右甚至更低),被动隔振方法效果不明显,主动控制不但难度很大而且还要付出高能耗和可靠性方面的代价[50-51].所以采用优化设计方法,从源头上尽量避免发生热诱发振动,更便于工程应用.最简单的措施就是通过增加反射涂层来减小输入热流.另外,也可以根据特定的需要做更复杂的优化设计[52-53].当然,最根本的解决办法是采用零膨胀材料来制造空间结构[24].但是在轨航天器的表面温度的变化范围在正负一百多度之间,怎样保证在这么大的温度范围内材料都有稳定的零膨胀性能,也是极具工程挑战性的任务.

由于热诱发振动产生的条件非常苛刻,所以验证试验的难度非常大.理想情况应该进行在轨试验[24],但要付出巨大的代价.所以通常还是开展地面试验,即便如此其难度和花费都是很高的[26-29].这种试验需要在热真空罐中开展,用红外灯阵模拟太阳热流,并最好用抽取遮阳板的方式来模拟从阴影到光照区的加热过程.此外在试验过程中要特别注意以下几点.

(1) 和空间太阳热流相比,在有限距离内红外灯阵产生的热流方向不是平行的,其分布密度还随灯与试件的距离而变化.因此需要考虑这些因素对试验结果的影响[3,27-29].

(2) 直射在热电偶上的热流会影响对试件表面温度测量的准确性,从而降低了薄壁构件截面温差测量结果的精度.因此需要精心设计热电偶的安装和温度补偿措施.

(3) 瞬态热流很难直接测量.通常是用测量温度根据热传导方程反算出热流随时间变化的曲线.但是由于热电偶测量的延迟效应,反演的热流变化速度会比真实情况慢.此时可通过热诱发振动的幅值对输入热流进行修正[28].

(4) 重力对柔性结构地面试验结果的影响很大.但由于要求试验必须在真空中进行,因此不能采用气浮装置消除重力.通常可采用侧向悬挂或竖直悬挂的方式来部分解决此问题.但是竖直悬挂试件的振动幅值会因为重力产生的恢复力而远小于真空中的幅值.侧向悬挂受重力的影响会小一些,但是因为悬挂装置不可能无限长,所以也会产生额外的约束,导致试验结果失真[28].

总之,由于热环境和重力等各种条件的影响,地面试验结果不能完全和在轨的真实结果吻合.在无法开展在轨试验的情况下,现在只能采用数值模拟和地面试验相结合的方法来预测在轨的热诱发振动响应[28].即,用地面试验的结果修正有限元模型,然后用有限元方法分析在轨真实环境下(比如失重状态)的结构响应.因此有限元模型和试验测试的精度就至关重要.

材料参数的准确性对数值模拟结果有很大的影响[54].但是一些热学参数测量的分散性比较大(特别是复合材料),而且力热参数通常是随温度变化的.采用随机有限元方法可以考虑材料参数的不确定性,但计算工作量很大,此时可以采用响应面方法来提高分析效率[53].若要在模拟过程中考虑参数随温度的变化,则需要增加额外的计算工作量.比如在隐式算法中增加额外的迭代步骤,或者直接采用时间步长较短(保证数值稳定性)的显式算法.不过,考虑到材料参数随温度变化的因素也是一个慢变量,而且热诱发振动往往是在进出地球阴影的较短时间内发生的(此时平均温度还没有发生太大的变化),那么也可以取所关心的温度范围内的参数平均值进行分析.但是材料参数的不确定性所造成的误差是否小于空间望远镜等高精度设备的要求,还是需要进一步讨论的.

6 结论

经过几十年的努力,人们虽然已经理解了热诱发振动现象的机理,但是在工程应用时还是面临着诸多挑战[6,23].特别是在研制空间望远镜等对指向性要求特别苛刻的航天器时,应该综合考虑光-热-结构-控制系统的一体化耦合分析[54].此时,将多个现有软件系统集成的方式已经不能满足这种高精度的要求,而应该发展专门的一体化数值模拟方法和与之配套的地面试验和验证技术.这正是未来需要努力的方向.

致谢

20 多年来,清华大学先后有多位老师与博士、硕士研究生参加了本课题组的工作或给予了宝贵的建议,他们是胡宁、任革学、岑章志、曹阳、丁勇、程乐锦、姚海民、黄彦文、李军、张晓东、张逸凡、唐羽烨、段进、李伟、范立佳、张军徽、樊孝清、袁小德和金邓格.他们的创造性研究和辛勤劳动,为课题的顺利完成做出了重要贡献,作者谨在此致以衷心的感谢.