考虑非线性本构的非刚性折纸结构动力学建模与分析1)

袁婷婷 任昆明 方雨桥 刘锦阳

(上海交通大学工程力学系,水动力学教育部重点实验室,上海 200240)

引言

折纸(origami)起源于传统艺术活动,泛指将平面二维材料通过折叠转变为空间三维结构的过程[1-3].近年来,折纸已发展成为一门新兴的学科,在航天[4-6]、生物医学[7-9]、建筑[10-12]、机器人[13-16]、材料科学[17-19]等诸多领域中发挥重要作用,这些研究利用了折纸结构良好的可折叠性、形状多样性、轻量小型等优点[20],与现代科学有机结合,表现出交叉性和复杂性的特点.随着信息技术、生物技术、新能源技术、新材料技术的交叉融合,折纸结构的研究得到了长足的发展,主要表现在几何设计、运动学分析和准静态分析等方面[21-23],但迄今为止,对折纸结构动力学研究尚未成熟,在动力学建模方法和理论分析上仍面临较大的困难和挑战[24].为了深度挖掘折纸结构的潜藏价值,开展折纸结构的动力学研究势在必行.

刚性折纸作为折纸的一个特殊子集,其数学模型的建立通常基于以下假设: 折痕是直线折痕,折叠面视为刚性,即不会发生拉伸或弯曲[25].目前,对刚性折纸的研究已经较为成熟,并已开发了多个软件[26-27].随着材料科学技术的不断发展,折纸结构在工程中的应用更为广泛,在很多情况下,折纸结构的折叠面会发生拉伸、弯曲或剪切等变形,甚至在展开过程中还会诱发接触碰撞等问题.因此,针对这类非刚性折纸结构,用刚性折纸模型进行模拟将无法反映非刚性折纸特有的力学性能.

考虑非刚性折纸结构的柔性效应,采用基于壳单元的有限元方法分析[28-30],是最为直接的一类建模方法.Yuan 等[6,31]基于绝对节点坐标的薄板单元,对具有大变形的折纸结构展开动力学中接触碰撞问题进行了研究,给出了折纸结构展开过程中的动力学响应和应力分布情况.有限元方法虽然能够给出包括应力分布在内的局部特征,但建模复杂度高,计算耗时长,较难推广到折纸结构动力学的性能优化和控制等工作.为此,有必要根据研究目的简化折纸结构的次要特征,建立出等效的非刚性折纸结构的动力学模型.近年来,国内外学者针对等效非刚性折纸结构开展了相关工作.文献[32]将折纸结构简化为弹簧–质点系统,即折叠面顶点为质点,折痕用弹簧代替.复旦大学方虹斌等[33-36]采用非线性弹簧等效动力学建模方法,并结合实验,开展了不同折纸结构和折纸超材料的动力学研究.对于另一类等效空间桁架模型,Yasuda 等[37]将非刚性折纸结构简化为一维运动的连杆结构,并结合最小势能原理,揭示了三角形圆柱折纸结构的双阱势能的特征.文献[38]较早提出杆–链模型,将折纸结构三角化为受旋转铰约束的桁架结构,开展运动学分析.在杆–链模型基础上,分别给杆和旋转铰分配恒定刚度,Wei 等[39]采用显示时间积分算法来模拟三浦折纸结构的弯曲.Fuchi 等[40-41]采用线性杆–链模型,实现对折纸超材料的拓扑优化.为了模拟折纸结构的大变形和位移,文献[42]基于超弹性本构的杆单元,提出了一种非线性杆–链模型,并对多种折纸结构进行准静态分析.Filipov 等[43]进一步细化离散方式,提升了非线性杆–链模型对非刚性折纸结构面外变形描述的精度.Dong 等[44]提出了一种将粒子–杆–弹簧模型与有限粒子法相结合的动力学模型,由折痕存储的能量驱动折纸结构展开.目前针对非线性本构的非刚性折纸结构动力学工作较少.为了分析超弹性非刚性折纸结构的动力学特性,需要建立一种通用且高效的动力学模型.

本文的工作重点是建立一种非刚性折纸结构的杆–链动力学模型,可适用于大变形和作大范围运动的折纸结构.第一节详细给出了非刚性折纸结构动力学建模过程.首先推导具有超弹性本构的杆单元的弹性内力阵.提出一种改进的卷簧本构模型,推导非线性卷簧单元的弹性力阵.最后,考虑阻尼效应,建立非刚性折纸结构多体系统动力学方程.第二节,将本文提出的非刚性折纸结构动力学模型分别应用于单菱形折叠、叶内折叠和Kresling 折叠这三种折纸结构中,并依次进行数值模拟,验证了杆–链动力学模型的准确性和高效性.在此基础上开展多稳态、瞬态动力学和波动力学特性分析.第三节对本文的研究工作进行总结,并对未来工作提出展望.

1 非刚性折纸结构动力学建模

本文将非刚性折纸结构简化为带卷簧的空间桁架结构,建立了杆–链模型,即将折痕和虚拟折痕等效为杆单元,杆单元相交的节点处用球铰连接,卷簧沿着杆的方向,如图1 所示.杆–链模型将折纸结构板面的拉伸和压缩用杆单元的变形来描述,采用卷簧来表征折痕的抗弯作用和折叠面的弯曲作用,该模型能够缩减计算规模,可高效地对非刚性折纸结构进行仿真,研究其丰富的力学行为.

图1 杆–链模型示意图Fig.1 The bar-and-hinge model

1.1 超弹性本构的杆单元

任意一个非刚性折纸结构均可简化为由一系列柔性杆件通过铰链组合起来的多体系统.为了表述方便,定义在惯性基下任一节点p的位置矢量坐标阵为xp,变形前的位置矢量坐标阵为Xp,节点位移矢量坐标阵为up=xp-Xp.

如图1 所示,杆单元e的广义坐标阵为

其中,xi和xj分别表示i节点和j节点在惯性基下的位置矢量坐标阵.取杆单元未变形时长度为Le,单元横截面积为Ae,则在局部坐标系下杆单元的弹性变形能[42]为

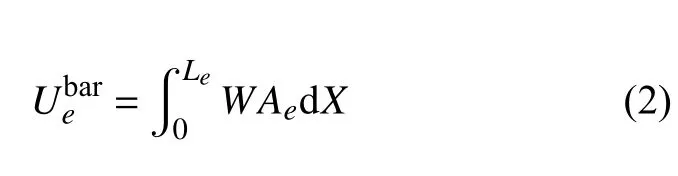
其中,W为应变能密度.由于杆单元是一维的,只需要考虑应力张量和应变张量的轴向分量.采用线性形函数,可以得到一维格林–拉格朗日应变 εx与单元节点位移ue的关系式[45]为

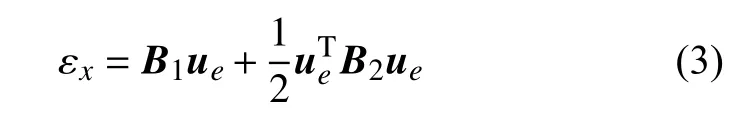
式中,ue,B1,B2可分别表示为

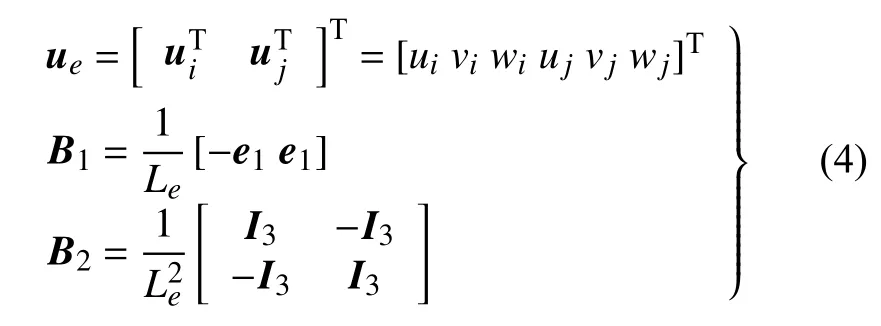
其中,e1=[1 0 0],I3是3×3 的单位矩阵.

设σx为沿x方向的Piola-Kirchhoff 应力分量,应变能密度的变分可表示为 δW=σxδεx.杆单元弹性变形能的变分为

将上式代入式(5),并得到杆单元的内力阵为

定义一维线性模量为

本文采用具有超弹性本构的杆单元,可适用于非线性材料,例如橡胶、硅胶等,能够处理大变形问题.本文采用Ogden 超弹性模型[46,42],其应变能密度为

其中,λ1,λ2,λ3分别代表右应变张量的三个特征值,F是变形梯度.N,μi,αi是材料参数.对于一维杆单元仅与λ1相关,且有

一维二阶P-K 应力σx和一维切线模量C由下式给出

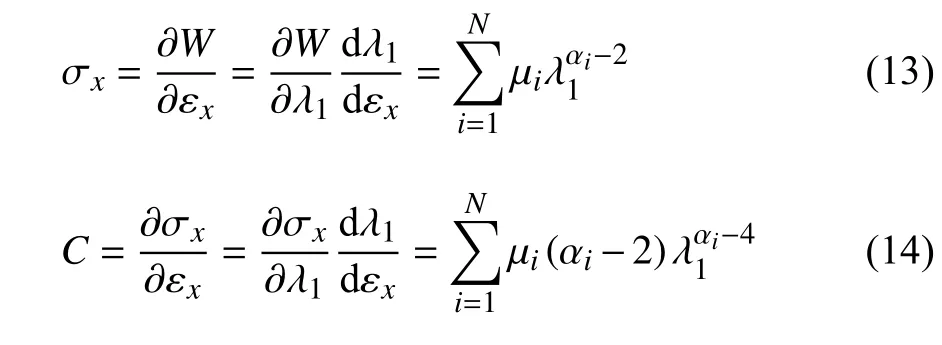
考虑到材料未变形时(λ1=1)为无应变无应力状态,有如下约束关系

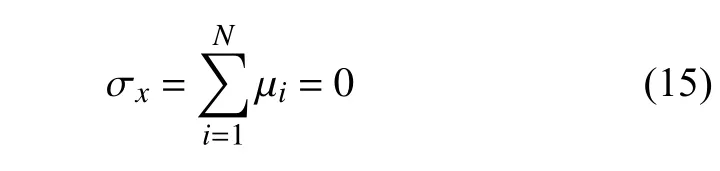
将式(15)代入式(14),可得未变形时一维模量为

在本文模型中,取N=2,给定α1,α2和C0,可根据式(15)和式(16)确定材料参数μ1和μ2.

假设杆–链模型中的杆单元为无质量杆,则将三角形折叠面的质量m均匀分布到三个节点上,即每个节点的质量为m/3,如图1 所示.三角形单元的质量阵为

其中,I9是9×9 的单位矩阵.

1.2 非线性卷簧单元

非刚性折纸结构的折痕,以及为描述折叠面弯曲添加的虚拟折痕,均采用非线性卷簧单元来建模.如图2 所示,卷簧沿着杆的方向,采用二面角进行度量[42],一个二面角至少需要三个向量才能描述,因此一个卷簧单元包括4 个节点和5 根杆.卷簧单元的广义坐标坐标阵为

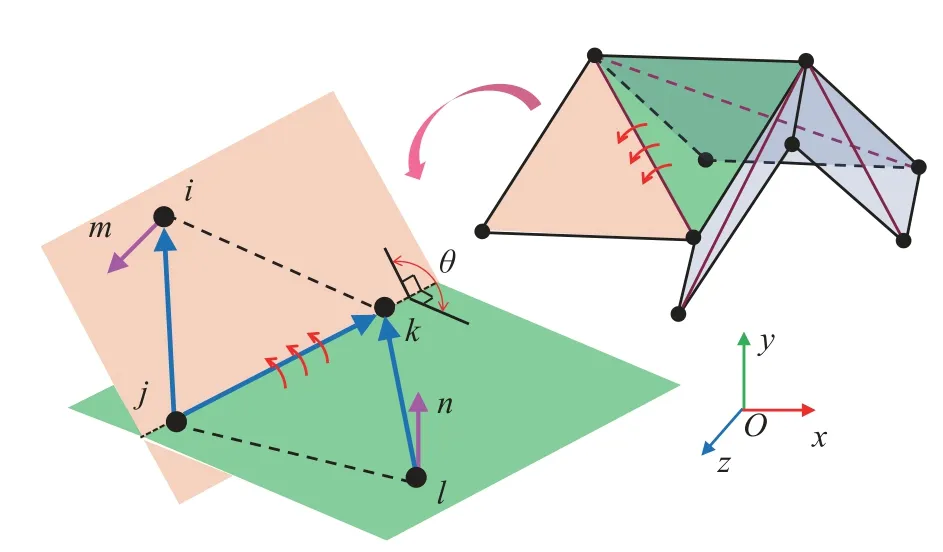
图2 卷簧单元示意图Fig.2 Rotational spring element

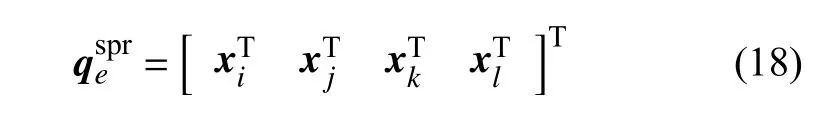
其中,xk和xl分别表示k节点和l节点的位置矢量坐标阵.则两个平面的法向量分别为

其中,定义rpq=xp-xq为相对位置矢量坐标阵,为rpq对应的坐标方阵.二面角 θ ∈[0,2π),可以表示为

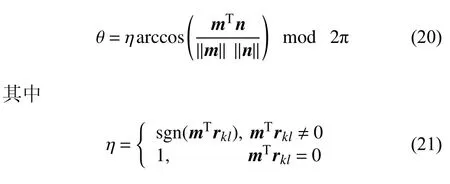
式中sgn 为符号函数.

将卷簧单元变形能对卷簧单元广义坐标阵进行变分,可以得到卷簧单元的内力阵为

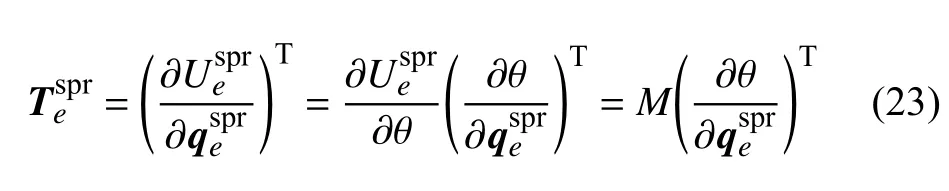
对卷簧单元的内力阵求变分,可得卷簧单元切向刚度阵

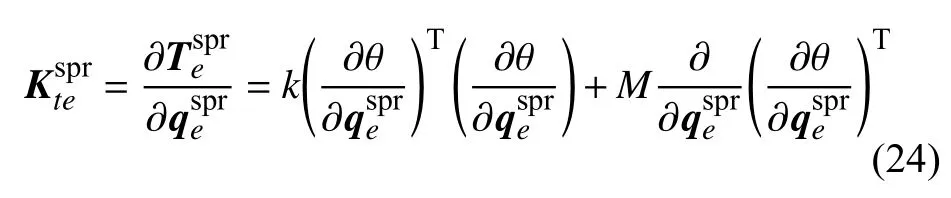
其中,k=∂M/∂θ 为卷簧切线刚度.

本文采用的卷簧为非线性卷簧,其特点是当二面角 θ →0,2π 时,力矩M→∞,能够避免折叠面的穿透问题.相较于传统的接触时施加约束的方法,此种考虑接触的方法更简洁方便,在数值仿真时不需要做其他调整,只需要建立合适的卷簧单元数学模型即可.

考虑到卷簧力矩的连续性,本文改进了非线性卷簧的本构模型,相较于传统的卷簧本构模型[42],该改进的本构模型在临近接触时延长了过渡区,如图3 所示.采用改进的本构模型求解动力学接触问题时,能够有效避免因时间积分步过大导致的穿透问题,则改进的本构模型中卷簧弯矩的具体表达式如下

图3 非线性卷簧单元的本构模型: 力矩与二面角的关系Fig.3 Nonlinear constitutive model of rotational spring: Dihedral angle θ versus moment M

其中,Ls为卷簧单元未变形时的长度,k0为卷簧线性部分的切线刚度.本文的数值算例中,均取a=100,b=0.4,c=0.8.

1.3 非刚性折纸结构动力学方程

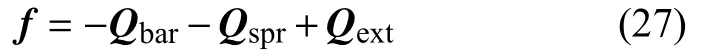
结合多体系统的约束条件 Φ=0,引入拉格朗日乘子阵λ,整理得到约束多体系统的动力学方程

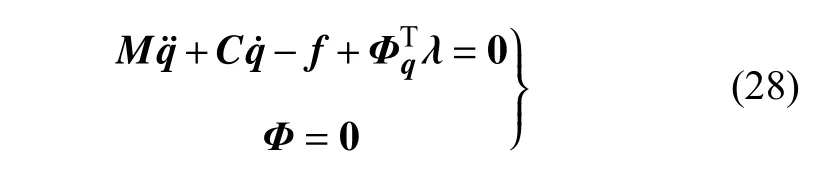
其中,系统的结构阻尼阵为C=αM,Φq=∂Φ/∂q为约束雅克比矩阵.

本文采用广义-α法[47]对式(28)的指标3 微分–代数方程组进行隐式求解.考虑到材料和卷簧的非线性本构,为了提高计算效率,采用了变步长[48-49]与预条件处理等计算策略.

2 数值算例仿真

将本文提出的非线性杆–链模型应用于三种经典的非刚性折纸结构的动力学分析中.第一个算例是进行单菱形折纸结构的动力学仿真,将杆–铰链模型分别与解析解、准静态以及有限元绝对节点坐标法ANCF[31]进行对比,验证杆-铰链模型的准确性和高效性.第二个算例是对叶内折叠折纸结构进行动力学仿真,并将刚性模型和非刚性模型的动力学结果进行对比分析.第三个算例是对Kresling 折纸结构进行仿真,揭示了折纸结构的多稳态和动力学特性.

2.1 单菱形折叠

为了验证杆–链动力学模型的正确性,选取的研究对象是一个简单的菱形折叠,包含四个节点,两个三角形面板和一条折痕,如图4 所示.菱形折叠中各节点的初始位置分别为:A(-0.07,0,0) m,B(0,-0.025,0) m,C(0,0.025,0)m,D(0.07,0,0) m,初始折叠角θ0=180o.此外,节点A,B,C均与惯性基固结,D点受到竖直向上的外力Fext,三角形板BDC会沿着折痕向上翻折.

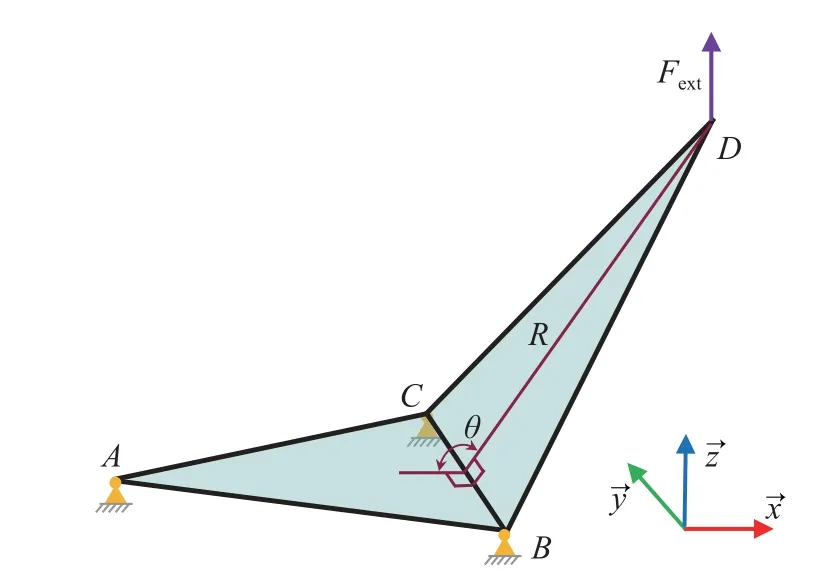
图4 单菱形折叠示意图Fig.4 A rhombus fold

采用杆–链模型,超弹性杆单元的材料参数分别为: 未变形时一维模量C0=1×107Pa,横截面积A=3×10-5m2,材料本构选取Ogden 超弹性模型,N=2,α1=5,α2=1.非线性卷簧单元的参数为:k0=0.012 5 N·m/rad,θ1=45o,θ2=135o.三角形面板的密度为1×103kg/m3,厚度为1 mm,忽略系统的结构阻尼.根据算例工况,在忽略重力的情况下,仅D点受到竖直向上的外力作用时,通过受力分析,得到外力载荷Fext与折叠角度θ的解析关系式为

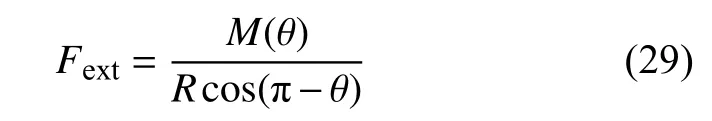
图5 给出了折叠角θ与外力载荷Fext的关系曲线.通过对比理论解和杆–链准静态的结果,Fext由0 逐步加载至1 N,可以观察到两组数据完全吻合,验证了杆–链模型的准确性.

对于动力学仿真,采用外载荷Fext=t2/9(N),计算0 s～3 s 时间内单菱形折叠的运动过程.观察图5发现,杆–链动力学模型的结果在准静态结果附近振荡较为明显,说明在动载荷作用下,对折纸结构进行动力学仿真揭示真实的动态特性的必要性.为了验证杆–链动力学模型的准确性,将该模型的结果与基于绝对节点坐标法的动力学结果进行对比,可以观察到两种方法的结果曲线基本重合.需要指出的是在本算例给定的参数下,折叠面不会发生明显的弯曲变形.接下来对比两种模型的计算效率,发现在相同计算机设置下,杆–链动力学模型的计算时间仅是ANCF 动力学模型的1/3,体现了杆–链动力学模型的高效性.

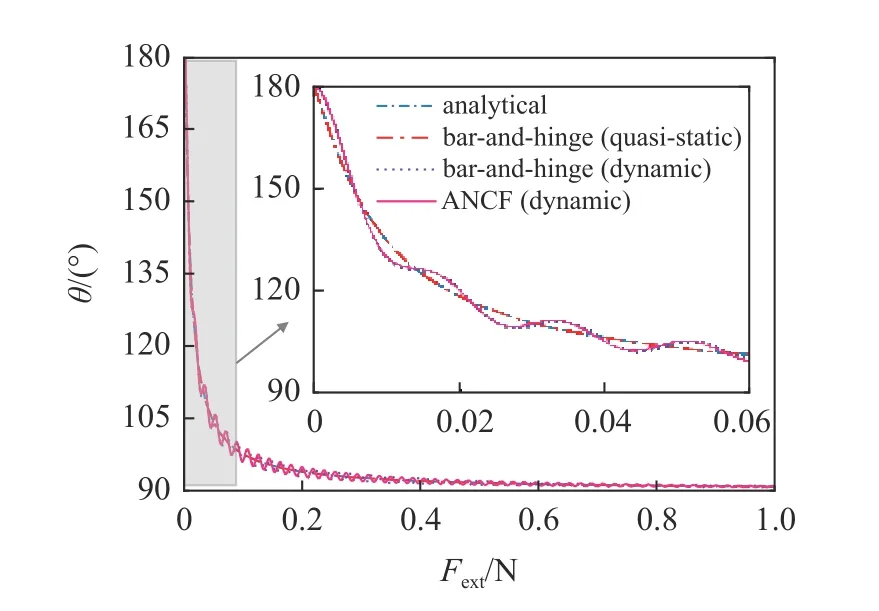
图5 单菱形折叠: 折叠角与外力的关系图Fig.5 A rhombus fold: Fext versus θ

综上所述,在折叠面未发生大变形的情况下,本文提出的杆–链动力学模型的精度足以反映折纸结构的动力学特性.此外,杆–链动力学模型的计算效率较高,有利于开展非刚性折纸结构的优化和设计等工作.

2.2 基于叶内折叠的折纸结构

大部分折纸的折叠方式灵感来源于自然界,De Focatiis 等[50]通过观察树叶的展开纹理,提出了叶内折叠的折叠法,该折叠图案的特点是具有很大的拉伸比,能够有效减少体积,可节省存储空间.本节将对基于叶内折叠的折纸结构动力学进行研究.

图6 所示为叶内折叠的折痕分布,其中直线表示山折,曲线表示谷折.将纸面固定在O-xy平面上,山折是将纸的两侧向z轴负方向折,折痕形成凸起;谷折是将纸的两侧向z轴正方向折,折痕形成凹陷.图6 右侧给出了叶内折叠折纸展开过程的实物图.

图6 叶内折叠的折痕分布Fig.6 Crease pattern of leaf-in origami

2.2.1 刚性折纸结构动力学分析

为了突出本文提出的非刚性折纸模型的优势,可以先对刚性的叶内折叠结构进行动力学分析,其中刚性折纸模型可参考笔者前期的工作[31],本文不再赘述.对于方型的叶内折叠,当施加沿着正方形对角线的大小相同的驱动约束时,考虑对称性,仅对1/8 构型进行研究即可.

根据叶内折叠的几何关系,以及刚性面任意两点的等距约束,可知系统的自由度 δ=-1,可判断出叶内折叠具有刚性不可展特征,因此需要释放至少2 个约束才能保证刚性展开.基于该前提,对叶内折叠添加2 条虚拟折痕,使得自由度 δ=1.其中折痕方式有四种,如图7 所示.

图7 叶内折叠添加虚拟折痕的方式Fig.7 Methods of adding virtual creases in leaf-in origami

设方型叶内折叠的边长为6cm,在G点施加的速度驱动,保证恰好在5 s 时从完全收拢到完全展开.在计算过程中,发现添加折痕的I,II 和III 方式在展开过程中均存在自锁现象,导致计算中止,得到的锁定构型如图8 所示.只有IV 方式的虚拟折痕添加方式,叶内折叠能够顺利展开.

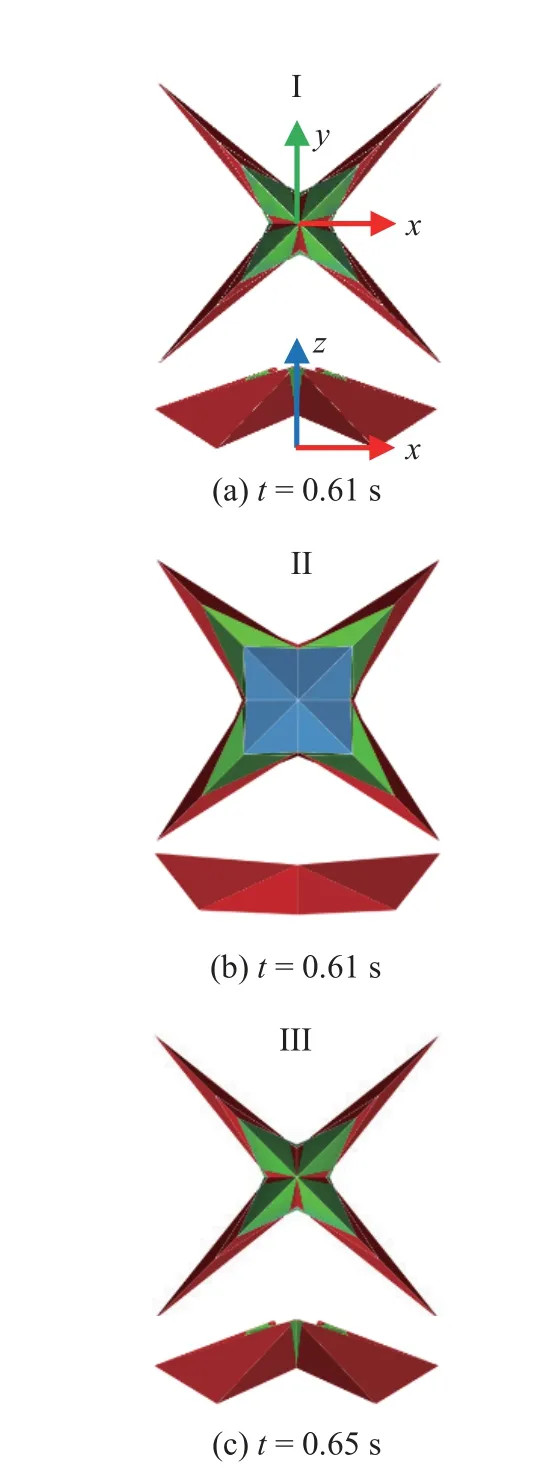
图8 I,II,III 方式下叶内折叠展开过程的奇异构型Fig.8 Singular configuration of leaf-in origami during the deployment in I,II,III cases

分别对叶内折叠展开和收拢过程进行数值仿真.采用IV 折痕添加方式,叶内折叠虽然在展开和收拢的计算过程中均未锁定,但是完全展开的构型是奇异构型,从而导致无法以该构型作为初始构型进行收拢计算.为此将t=4.99 s 时刻作为收拢计算的初值,避开奇异构型,实现叶内折叠收拢过程的计算.

如图9 所示,将数值求解的结果与ADAMS 仿真的结果进行对比,验证了刚性折纸动力学模型的准确性.在Step1 展开过程中,即t∈[0,5] s,刚性叶内折叠的zA并不是随时间单调递增的,而是呈现先增加,再减小,最后再增加的趋势.通过观察展开过程的构型图发现,最内层向下翻折,zA减小,这是因为第三层在展开时受刚性折纸的等距约束的影响.对于Step2 收拢过程,即t∈(5,10] s,由于对收拢过程与展开过程施加的驱动大小相等,仅方向相反,可以观察到刚性叶内折叠的zA与展开过程呈对称分布.

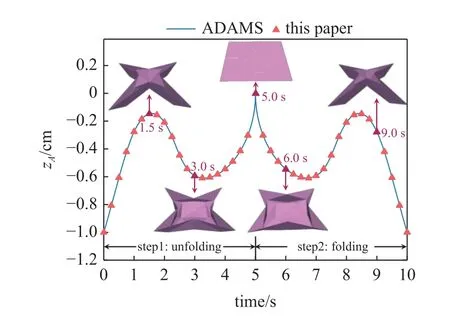
图9 叶内折叠展开和收拢过程中A 点z 坐标时域图Fig.9 Time history of z coordinate of point A of leaf-in origami during unfolding and folding process

针对刚性不可展问题,本文给出了添加虚拟折痕和修正初始构型的方法,有效解决了展开和收拢过程的锁定问题.本文对刚性折纸结构的可展性和动力学研究,为工程问题中折纸结构的运动控制和设计优化提供理论指导.

2.2.2 非刚性折纸结构动力学分析

本节将基于杆–链模型,对非刚性叶内折叠折纸结构的展开过程进行动力学仿真.如图10(a)给出了叶内折叠的初始收拢构型,并且四个角点P1,P2,P3,P4均受到沿对角线方向向外的位移驱动d(t),具体表达式为

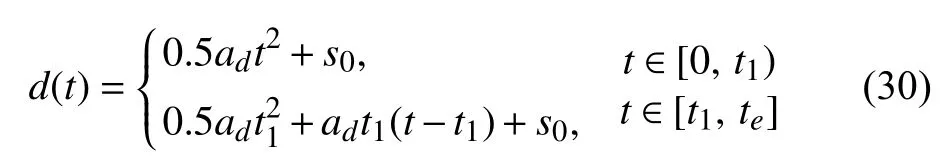
其中,ad=0.276 cm/s2,s0=3 cm,t1=1 s,te=10 s.该参数能够保证在t=5 s 时,叶内折叠的刚性折纸模型恰好完全展开.

针对非刚性杆–链动力学模型,超弹性杆单元的材料参数分别为: 未变形时一维模量C0=1×107Pa,横截面积A=1×10-5m2,材料本构选取Ogden 超弹性模型,N=2,α1=5,α2=1.如图10(b)所示,添加了弯曲折痕以描述折叠面的弯曲.设弯曲卷簧的折痕刚度为折痕卷簧刚度为0.001 N·m/rad,为了避免穿透现象发生,即要求二面角不能出现0 和2π,取θ1=ε,θ2=2π-ε,ε=0.000 5 rad.折叠面的密度为1420 kg/m3,厚度为0.5 mm,取系统的结构阻尼系数为α=1.5.

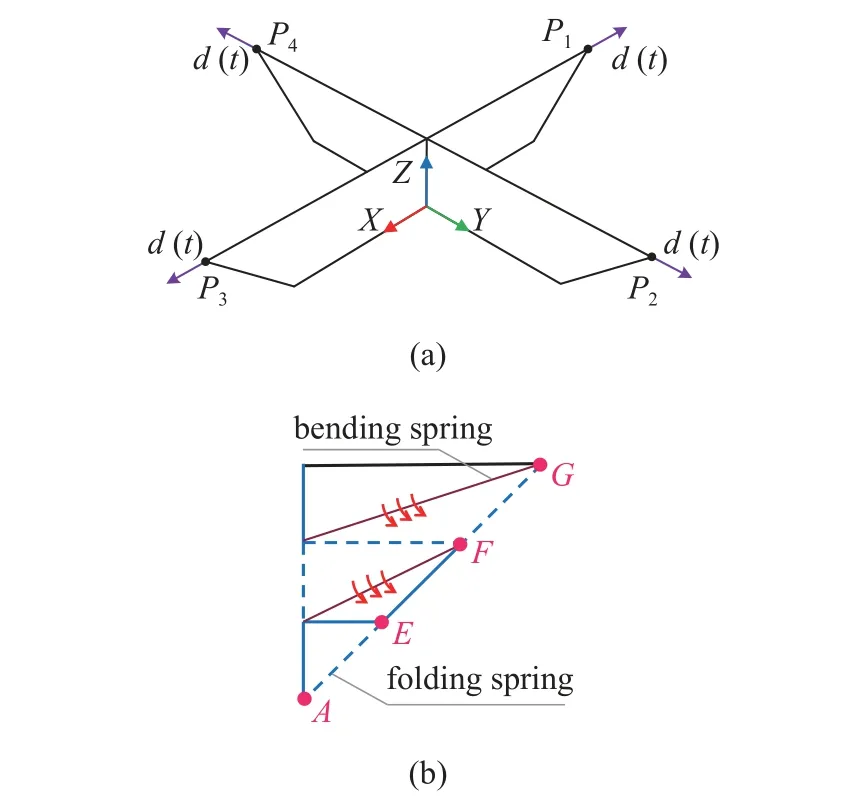
图10 叶内折叠: (a)初始构型;(b) 1/8 模型卷簧分布Fig.10 Leaf-in origami: (a) Initial configuration and (b) spring patter in 1/8 model

图11 给出了在相同驱动下,分别采用刚性和非刚性折纸模型模拟的叶内折叠展开过程的构型图.可以观察到,刚性折纸模型在t=5 s 时,恰好能够完全摊平,但受限于完全展开时处于奇异位置,计算中止.在非刚性折纸模型中,由于考虑了折叠杆的轴向变形以及折痕处卷簧刚度,展开过程有所滞后.在叶内折叠完全展开后,持续施加位移驱动,非刚性的叶内折叠的各杆单元发生明显的轴向拉伸变形,并且变形程度由中心向外逐渐变大.

图11 叶内折叠: 刚性与非刚性折纸模型展开过程构型图Fig.11 Leaf-in origami: Configuration of the rigid and non-rigid origami models during the deployment

图12 分别给出了A点z坐标的位置、速度和加速度时间历程图.图12(a)显示,刚性折纸模型在展开过程中,会出现最内层向下翻折的现象,即zA呈现先增加后减小的趋势.但在非刚性折纸模型中,叶内折叠因柔性效应能直接拉开,zA单调增加到0,而后发生振动,最后振荡逐渐衰减直至为0.由图12(b)和图12(c)可知,刚性折纸模型在接近t=5 s 时,速度与加速度会突增,无法收敛,临近自锁状态.对于非刚性折纸模型,观察到在展开的初始阶段数值出现振荡,这是由于叶内折叠在初始构型时,折面存在接触.由此可知,非刚性折纸模型相较于刚性折纸模型具有更好的数值模拟通用性,不仅能够避免自锁问题,揭示刚性折纸无法给出的动力学特性,还能给出具有大变形的张紧构型,更贴合实际情况.

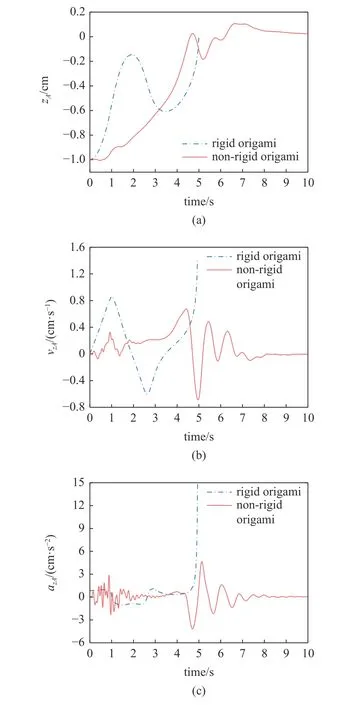
图12 叶内折叠: A 点z 坐标的 (a)位置;(b)速度;(c)加速度时域图Fig.12 Leaf-in origami: Time histories of z coordinate of point A of(a) position,(b) velocity and (c) acceleration

为了进一步分析非刚性叶内折叠折纸结构展开过程的动力学特性,选取了1/8 模型中对角线上的A,E,F,G四个点为观测点,分别给出z坐标位置的时间历程图,如图13 所示.可以观察到,点G作为驱动作用点,在运动过程z坐标保持不变.在叶内折叠展开过程中,点A,E,F在z方向都会存在不同程度的振荡,并且距离中心点越近,其展开过程振荡就越为显著.由此可知,叶内折叠在展开过程中,中心点发生振荡的振幅很明显,采用本文提出的杆–链动力学模型,能够揭示折纸结构的丰富的动力学行为.

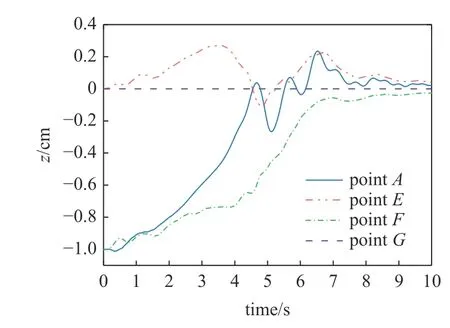
图13 叶内折叠: 点A,E,F,G (图10) z 坐标时域图Fig.13 Leaf-in origami: Time history of z coordinate of points A,E,F,G (see Fig.10)

2.3 基于Kresling 折叠的折纸结构

Kresling 折叠是一类具有多稳态特性的柱状折纸,已广泛应用于工程中,如爬行机器人、机械臂、人造肌肉驱动器等,因此对其力学性能的探究很有现实意义.

图14 给出了Kresling 平面折痕分布和柱状结构,满足以下几何关系

图14 Kresling 折叠: (a)折痕分布;柱状结构: (b)主视图,(c)俯视图Fig.14 Kresling origami: (a) crease pattern.Columnar structure:(b) front view and (c) top view

其中,m表示柱状结构的胞元数,n表示圆柱的边数,a和R分别为n边形的边长和外接圆半径.在此基础上,再给定单胞高度h和相邻胞元的错位角θ,则能够确定Kresling 折叠的几何结构.

2.3.1 不同多边形Kresling 结构的准静态分析

采用杆–链模型对非刚性Kresling 结构进行准静态分析,超弹性杆单元的材料参数分别为: 未变形时一维模量C0=5×107Pa,横截面积A=1×10-5m2,选取Ogden 超弹性模型,N=2,α1=5,α2=1.非线性卷簧单元的参数为:k0=1 N·mm/rad,θ1=45o,θ2=315o.将Kresling 底部的各个节点与惯性基固结,在顶层各节点施加竖直向下的轴向载荷,不计重力的影响.

为了分析多边形边数对Kresling 柱状结构力学特性的影响,分别取双胞(m=2) 的正六边形(n=6)、正八边形(n=8)和正十边形(n=10)进行分析.已知外接圆半径R=0.05 m,错位角θ=45o,胞元高度h=0.05 m.本文采用改进的广义位移控制法[51]解准静态过程,能够较为平滑地过渡极值点,并揭示结构的多稳态现象.

图15 分别给出了在正六、八、十边形Kresling折纸压缩过程势能和力随位移变化的曲线.由图15(a)可以看出,这三条势能曲线都包含两个阱,即state(0)和state(1),对应的力–位移曲线(图15(b))出现两次正向穿越Fext=0 的水平轴,呈现出了Kresling 结构的双稳态特征.可知,多边形边数n对Kresling 结构的稳定性特征很敏感.其中,三种折纸结构的稳态state(0)和state(1)对应的构型分别在图15(a)中给出.

在图15(b)中,A为未加载荷时的初始构型.B1,B2,B3,D1,D2,D3为外力极大值点;C1,C2,C3为外力极小值点;E1,E2,E3为准静态仿真过程中所能到达的位移最大点.针对于上述特殊点,给出了对应的Kresling 构型图,如图16 所示.

图16 Kresling 折叠: 不同多边形中特殊点处(见图15(b))构型图Fig.16 Kresling origami: Configuration of special points (see Fig.15(b)) in different shapes

通过对比图15(b)中的三条力–位移曲线,可知在加载过程中(阶段①和③),边数与斜率呈正相关关系,说明随着边数的增加,Kresling 构型的轴向刚度越大.观察到正六边形的曲线相较于正八和正十边形呈现更复杂的非线性关系.综上所述,不同多边形改变了Kresling 的几何设计,这些差异会对结构的刚度有着显著影响.增加边数n,Kresling 结构的刚度就越大,在不同稳态构型(三角形标记)切换过程中所需的外力越大,因此可以通过改变边数来调整结构的稳定性,可为折纸结构的设计提供参考.

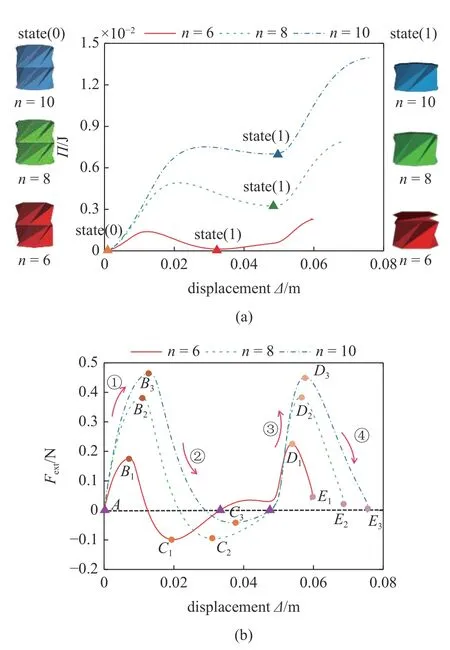
图15 Kresling 折叠: 不同多边形下,(a)势能曲线,(b)力–位移曲线Fig.15 Kresling origami: (a) Potential energy curve and (b) forcedisplacement curve in different shapes

2.3.2 位移驱动下Kresling 结构的动力学分析

在上一节中采用准静态模型研究了Kresling 的双稳态特性,并分析了不同边数下柱状Kresling 结构的力学特性,接下来将采用非刚性杆–链模型对Kresling 结构进行动力学分析.如图17 所示,本节选取双胞正十边形Kresling 折叠的折纸结构作为研究对象,底层的十个节点与惯性基固结,顶层的十个节点受到相同的位移驱动d(t),方向竖直向下.取系统的结构阻尼系数为α=1.5.引入Kresling 胞元应变的概念,则胞元e的应变定义为 εe=(he-h0)/h0,其中he和h0分别表示胞元e当前时刻和初始时刻的高度.非线性杆–链模型的参数选取与2.3.1 一致,采用广义-α法求解动力学方程,计算时间te=4 s.

图17 正十边形Kresling 折纸结构Fig.17 Kresling origami structure in regular decagon

取P1,P2,P3为观测点,分别描述顶层、中间层和底层的动力学特性,其中h1和h2分别为上、下两个胞元的高度.图18(a)给出了z坐标的时间历程图,点P1的曲线为施加在顶层各节点的位移驱动,即在0～1 s 为加速阶段,加速度为0.03 m/s2,随后以0.03 m/s 的速度匀速下压,有zp1=h1+h2.此外,点P3为约束点,限制z=0.为了比较本文提出的卷簧本构模型与传统的卷簧本构模型[42]的区别,图18(a)给出了在两种模型下点P2的运动轨迹,可知在采用传统的卷簧本构模型时,会出现明显的单元穿透问题,即h2出现跨单元情况.选取t=3.5 s 时刻下两种模型在state C 和state D 处的构型图,可观察到本文提出的卷簧本构模型能够保证Kresling结构在压缩过程中不会出现穿透.这说明了在接触碰撞动力学问题中,改进的卷簧本构模型更具鲁棒性.

通过观察图18(a)中点P2的运动轨迹,发现不论是本文的卷簧本构模型还是传统的卷簧本构模型,都在h2=0.023 m 处出现不稳定的振荡,对应的state A 和state B 的构型图如图18(b)所示.观察曲线可知,本文模型的振荡振幅会逐渐衰减直至达到完全压缩状态,然而传统的卷簧本构模型会发生明显的振荡,并伴随单元穿透问题.为了解释这一振荡现象,图19 给出了Kresling 压缩过程的应变能云图.观察到应变能云图关于对称轴h1=h2对称.在位移驱动作用下,应变能逐渐增大,Kresling 结构的压缩路径趋向于最小应变能的方向.在h2=0.045 m 处,最小应变能路径出现拐角,偏离对称轴,此时压缩主要体现在顶层单元压缩.由于惯性的存在,点P2的压缩运动滞后于点P3,因此压缩路径在对称轴上方.由2.3.1 节可知Kresling 结构具有多稳态特性,初始时刻应变能最小,对应稳态state(0),另一个稳态state(1)则存在于压缩过程中.因此,在未到达state(1)前,应变能减少,但外驱动力仍在做功,为满足能量守恒定律,则动能增大出现振荡.此外,在压缩过程中,原路径方向会遇到高应变能区域的阻碍,导致路径发生转向,这也是发生振动的诱因之一.

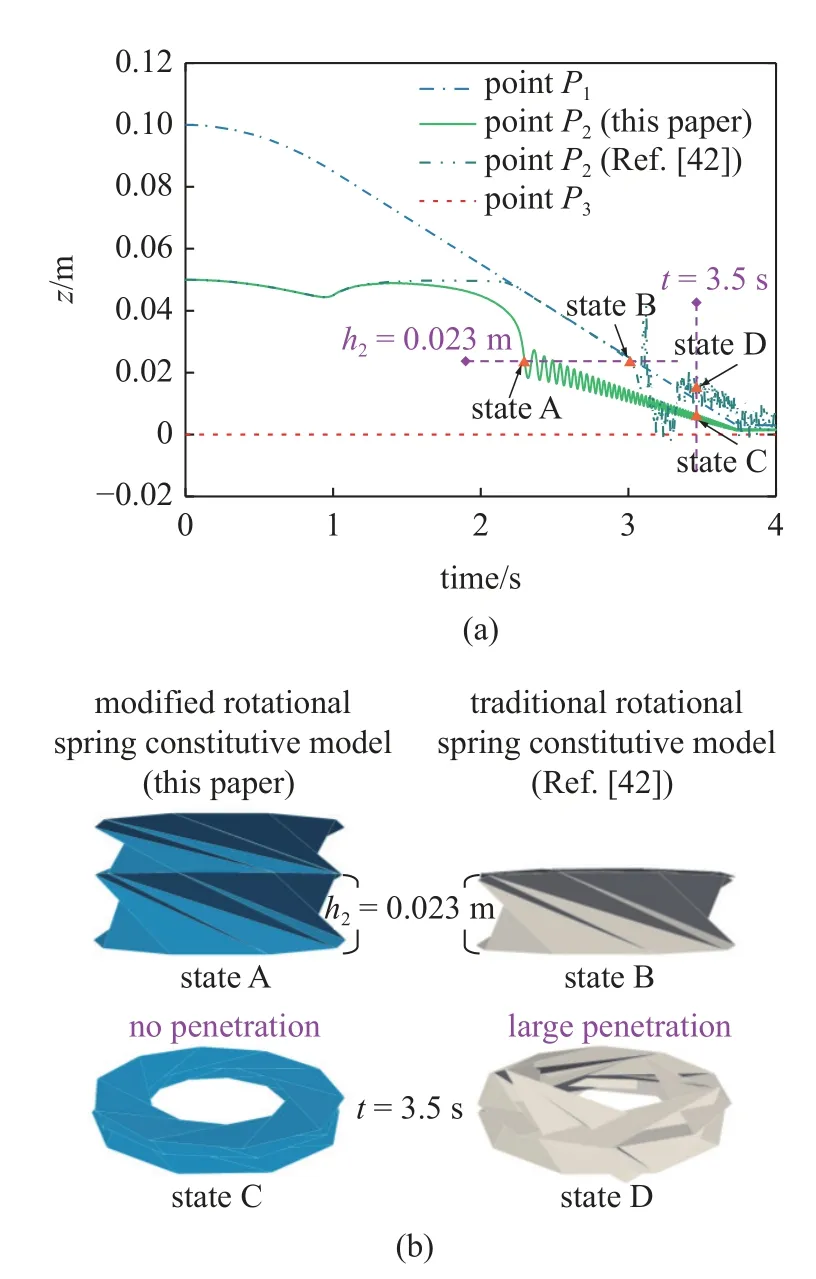
图18 正十边形Kresling 折叠: (a) z 坐标时域图;(b) 不同卷簧本构模型中特殊点处(见图18(a))的构型图Fig.18 Regular decagon Kresling origami: Time histories of (a) z coordinate;(b) configuration of special points (see Fig.18(a)) in different rotational spring constitutive models

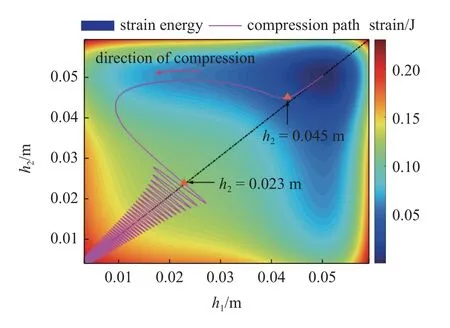
图19 正十边形Kresling 折叠: 应变能云图Fig.19 Regular decagon Kresling origami: Strain energy cloud map

为了进一步分析压缩过程的动力学特性,图20给出了底层点P3处法向约束反力FN的时间历程图.由图可知,Kresling 折纸结构在未达到稳态State(1)前,FN的变化曲线较为稳定,但是随着外驱动的不断加载,临近稳态State(1),FN开始抖动,并且振幅与数值都在不断增加.此外,在接近于完全压缩时,会发生折叠面的接触碰撞,从而导致FN数值振荡的加剧.综上所述,由动力学仿真的结果可知,Kresling 的双稳态直接影响了结构的稳定性.并且在接近于极限折叠(完全压缩)时,由于接触碰撞,其力学本构呈现非光滑的特征,进而伴随出现复杂的非线性问题.

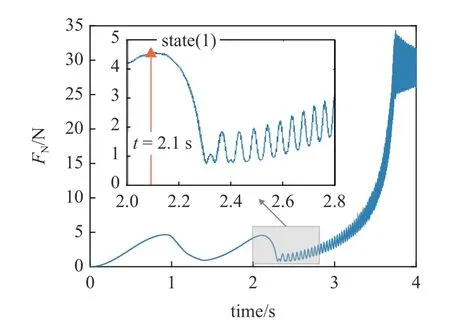
图20 正十边形Kresling 法向支座反力FN 时域图Fig.20 Time history of the normal support reaction force FN of the regular decagon Kresling origami

2.3.3 正弦激励下多链Kresling 折纸结构的波动力学分析

在2.3.1 和2.3.2 节中,对双胞Kresling 折纸结构的准静态和动力学进行了研究,揭示了其双稳态特性和复杂的动力学行为.在本节中,采用非刚性杆–链动力学模型,对一种由Kresling 胞元组合成的多链超材料折纸结构进行动力学分析.将该多链折纸结构视为波传播的媒介,讨论其在正弦激励下的波动力学特性.

如图21 所示,选取30 胞元(m=30)的正六边形(n=6)多链Kresling 结构为研究对象,其中外接圆半径R=0.03 m,错位角θ=45o,胞元高度h0=0.03 m.在杆–链模型中,超弹性杆单元的材料参数与2.3.1 一致,非线性卷簧单元的参数为:k0=0.02 N·m/rad,θ1=5o,θ2=355o.将单层Kresling 结构作为多链超材料折纸结构单胞,胞元的应变表达式见2.3.2 节.取系统的结构阻尼系数为α=1.5,忽略重力作用.将底层各节点与惯性基固结,顶层各节点受到相同的正弦位移激励d(t)=0.02sin(5πt) (m),方向沿着z负方向,激励时长为0.05 s.采用广义-α法求解系统的动力学方程,计算时间te=0.4 s.

图21 多链Kresling 折纸结构波动力学Fig.21 Wave dynamics of multi-chain Kresling origami structure

图22 给出了不同时刻多链Kresling 折纸结构的应变–构型图,其中蓝色代表压缩,红色代表拉伸.初始时刻应变为0,右端受到挤压正弦位移激励作用.很明显地观察到,在t=0.15 s 之前,压缩应变逐渐从右端传递到左端,经历过主压缩后的胞元,会出现出不同程度的拉伸应变.因左端约束作用,在主压缩应变传递到单元30 后,会被吸收和反射后再次作用于多链中,可观察到胞元的应变呈现无规律的交替压缩和拉伸.由上述现象可知,压缩正弦激励会产生应变波,在多链Kresling 折纸结构中传播,并发生多重应变波的叠加,导致胞元产生压缩和拉伸的波动变化.

图22 多链Kresling 折纸结构的应变–构型图Fig.22 Strain-configuration of multi-chain Kresling origami structure

为了更直观地分析多链Kresling 结构的波动力学行为,图23 给出了应变波传播过程的时空变化图.观察到主压缩波沿着单元数递增的方向传播,在到达单元30 后,主压缩波会被反射,并且振幅会出现衰减.此外,在主压缩波区域外,出现多条拉伸应变波,其波峰数值小于压缩波,并且在传播过程中呈现不连续现象.随着压缩和拉伸波在多链Kresling 结构中的传播和叠加,结构的波动力学行为更为复杂,揭示了折纸超材料中波传播的特性.

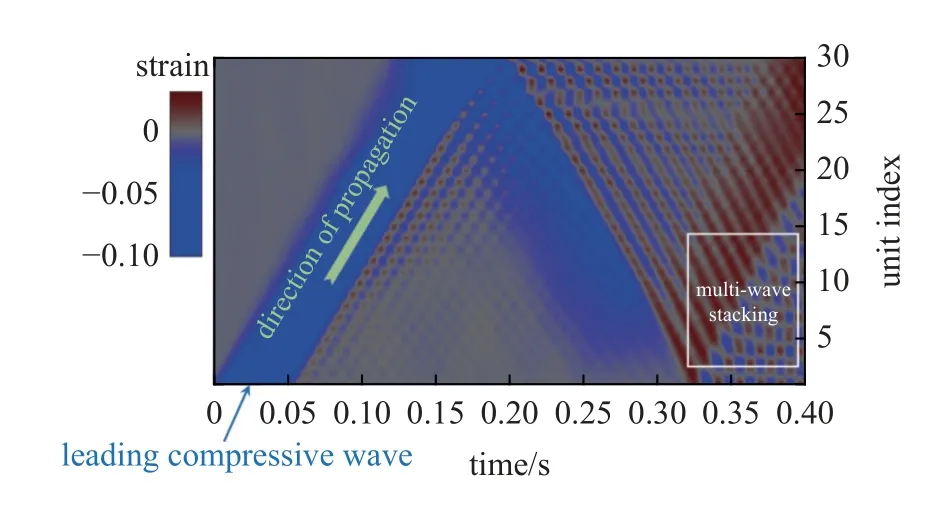
图23 多链Kresling 折纸结构应变波传播的时空图Fig.23 Space-time of strain wave propagation in multi-chain Kresling origami structure

图24 描绘了多链Kresling 折纸结构中不同单元的应变时间历程图.初始时刻,在正弦压缩冲击下产生主压缩应变波,随着时间推移,逐渐向后续的折纸胞元传播.从图中观察到,胞元在经历主压缩波后,会出现拉伸与压缩的振荡,并且拉伸的幅值越靠近约束段越大,伴随多重应变波的叠加,应变曲线呈现出复杂的非线性特性.

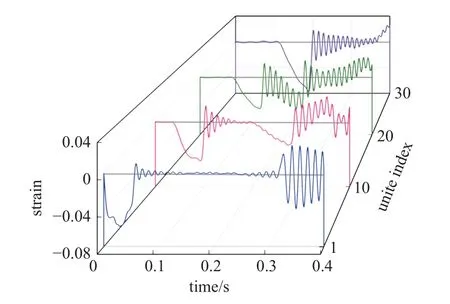
图24 多链Kresling 折纸结构: 不同单元的应变时间历程图Fig.24 Multi-chain Kresling origami structure: Strain versus time curves in different unites

为了进一步对多链Kresling 折纸结构吸能特性进行研究,将仿真时间延长至1 s,图25 给出了能量–时间曲线图.在t=0.05 s 时,位移激励释放,外力将不再做功,系统总能量保持不变.很明显地观察到,结构的弹性势能和动能的振幅逐渐减少,耗散能逐渐增大.一般地,耗散能主要包括结构阻尼耗散能、摩擦耗散能、黏性耗散能等.观察弹性势能和动能的曲线,发现这两条曲线的振荡频率与振幅大小衰减的基本一致,并且相位相反.由结果可知,在位移激励释放后,系统能量耗散较为明显,说明了Kresling折纸结构具有较好的吸能和减震的功能.

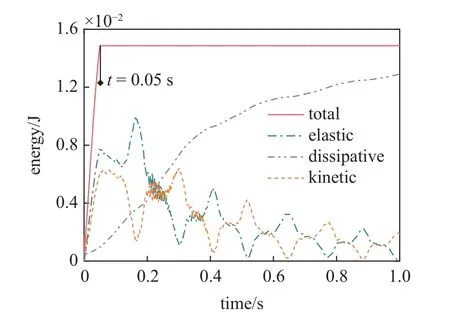
图25 多链Kresling 折纸结构的能量–时间曲线Fig.25 Energy-time curves of multi-chain Kresling origami structure

综上所述,采用本文提出的杆–链模型,能够揭示非刚性多链Kresling 折纸结构的波动力学特性,描述应变波在折纸结构中的传播过程,并揭示波的传播与叠加规律.通过能量分析,体现了Kresling折纸结构吸能和减震的特点,可为冲击缓冲和能量收集的折纸设计提供理论依据.

3 结论

随着材料科学技术的不断发展,非刚性折纸结构在工程中的应用越来越广泛.本文把非刚性折纸结构简化为带卷簧的空间桁架等效结构,建立了一种通用且可处理的非线性杆–链动力学模型.基于Ogden 超弹性本构关系,推导了杆单元的非线性弹性力阵和切线刚度阵,并将折痕和虚拟折痕等效为杆单元,可处理折纸结构的大变形和大范围运动问题.接下来,采用具有非线性旋转刚度的卷簧来模拟折痕的抗弯作用和虚拟折痕的弯曲作用.为了有效解决接触碰撞动力学中折叠面的穿透问题,改进了卷簧的本构模型,相较于传统的卷簧模型,具有更强的通用性和鲁棒性.在此基础上,推导了广义质量阵,并考虑阻尼效应,用虚功原理建立了非刚性折纸结构多体系统的动力学方程.

本文将提出的杆–链动力学模型应用于三种经典的非刚性折纸结构中.第一种单菱形折纸结构,通过比较准静态与解析解的结果,验证了杆–链模型的准确性,随后与基于绝对节点坐标法的动力学仿真结果进行对比,说明了杆–链动力学模型的准确性与高效性.第二种是基于叶内折叠的折纸结构,首先采用添加虚拟折痕和修正初始构型的方法,有效解决了刚性折纸模型中展开和收拢过程的锁定问题,对刚性折纸的可折叠性和奇异问题进行讨论.然后,将非刚性与刚性折纸模型进行对比,发现非刚性折纸模型不会发生自锁现象,体现了柔性变形对折纸结构大范围运动的影响,此外还能够给出具有大变形的张紧构型,更具通用性.第三种是Kresling 折纸结构,首先对不同边数下Kresling 结构进行准静态分析,发现了Kresling 的双稳态特性.接下来对位移驱动下的Kresling 折纸结构进行动力学分析,揭示了在多稳态影响下诱发的非线性动力学行为.最后,基于Kresling 单胞发展一种多链超材料折纸结构,并展现了在正弦激励作用下结构的波动力学特性,揭示应变波的传播和叠加现象,通过能量分析,体现了Kresling 折纸结构吸能和减震的特点.

本文提出的杆–链动力学模型,有效简化了非刚性折纸结构的动力学建模过程,能够较为准确和高效地对非刚性折纸结构的动力学进行数值模拟,揭示丰富的非线性动力学特性.未来可将该杆–链动力学模型拓展到非刚性折纸结构的优化设计和动力学控制中.