北斗卫星导航系统静态精密单点定位精度分析——以我国南部地区为例

朱强，宋传峰，刘思敏

（1.广州市城市道路养护管理中心，广东 广州 510030；2.武汉大学 卫星导航定位技术研究中心，湖北 武汉 430079）

我国自主建设、独立运行的北斗导航卫星系统（BDS）已于2020年7月31号正式运行，并向全球用户提供服务[1]。目前已形成美国GPS、俄罗斯格洛纳斯（GLONASS）、欧洲伽利略卫星导航系统（Galileo）和中国BDS四大全球导航卫星系统（GNSS）共存的局面。相对于GPS、GLONASS和Galileo，BDS由地球静止轨道（GEO）卫星、倾斜地球同步轨道（IGSO）卫星和地球中轨道（MEO）卫星3种混合星座构成。BDS独特的星座结构设计，使其同时具备导航和通信功能，且可显著增强我国尤其是南部地区的定位能力。随着港珠澳大桥、粤港澳大湾区等重大国家工程或战略的实施，我国南部地区对卫星导航系统的服务需求日益增长。GNSS系统，尤其是BDS，将在大型基础设施变形监测、地理信息应用、海洋开发、石油探测[2-4]等方面发挥重要作用。

精密单点定位（PPP）具有全球无缝导航、应用成本相对低廉等显著优势。在南北极、海洋、沙漠、高原等特定区域，PPP更是控制测量、冰盖运动监测等应用的重要可选手段[5]。相对于双差处理模式（GAMIT软件采用该模式），非差数据处理模式具有处理速度快[6]、无需分网解算等优势，且具有一定的精度保证。Bernese、GIPSY、PANDA等GNSS数据处理软件均支持非差数据解算[7]。已有大量文献对GPS与BDS的PPP模型和算法进行了研究和分析[8-10]；但鲜有文献从实际应用的角度对GPS与BDS的PPP进行分析和比较，尤其是针对我国南部地区GPS、BDS的PPP服务性能评价更是相对空白。目前，我国实际工程应用较多的仍为GPS，BDS的实际应用能力需进一步评价和分析。

针对上述现状，本文选择我国南部沿海某工程的3座B级GNSS观测站数据进行处理和分析，点号命名为B001、B002和B003，其中B001点可同时跟踪BDS-2和BDS-3信号，B002点和B003点暂时无法跟踪BDS-3信号。本文首先从24 h（单天）和2 h观测数据时长的角度出发，分别对GPS、BDS及其GPS/BDS组合的静态PPP应用性能进行评估；然后分析PPP计算的CGCS2000坐标精度，可为实际工程应用提供参考。

1 PPP数学模型

本文主要介绍GPS、BDS及其组合PPP的定位模型和数学推导，包括函数模型和随机模型。

1.1 函数模型

对于BDS卫星j，接收机在B1和B3频率（精密轨道和精密钟差产品基于该频率观测数据生成）上的伪距和载波相位观测值[11]为：

式中，Pi、Φi分别为Bi频率的伪距和已转换为距离的载波相位观测值，单位为m；ρ为站星间几何距离，单位为m；c为光速，单位为m/s；dtC、dT分别为接收机钟差和卫星钟差，单位为s；C为BDS；dorb、dtrop分别为卫星轨道误差和对流层延迟，单位为m；dion/Bi、λi分别为Bi频率上的电离层延迟和波长，单位为m；Ni为Bi频率的相位模糊度，单位为周；分别为Bi频率上伪距和载波相位的多路径效应，单位为m；分别为Bi频率上伪距和载波相位的硬件延迟，单位为m；ε为观测噪声，单位为m。

由于包含接收机和卫星的初始相位延迟，相位模糊度Ni并不是整数；且考虑到精密卫星钟差产品中包含了卫星端的硬件延迟[12]，观测值方程中仅考虑接收机端硬件延迟即可。BDS卫星使用码分多址，接收机对每颗卫星的硬件延迟相同，因此观测方程中的硬件延迟项可表示为：

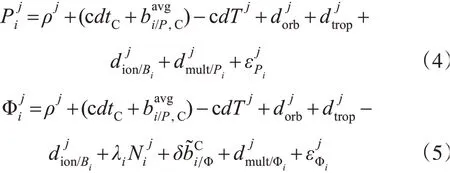
类似的，对于GPS卫星k，接收机在L1和L2频率上的伪距和载波相位观测值可表示为：

式中，G为GPS卫星；λi为Li频率上的波长，单位为m。

经GPS和BDS精密轨道和精密钟差改正并忽略多路径效应后，伪距和载波相位消电离层组合观测值为：

式中，PIF和ΦIF分别为伪距和载波相位消电离层组合观测值，单位为m；NIF为消电离层组合模糊度。

式中，为接收机钟差和伪距硬件延迟组合；为模糊度和伪距相位硬件延迟差的组合。

GPS与BDS组合定位时，可将BDS的接收机钟差表示为[13]：

式中，为接收机GPS时与BDS时的系统偏差，在短时期（单天）内可认为是一稳定值。

此时，BDS观测方程为：

式（12）、式（13）为GPS的PPP函数模型，式（14）、式（15）为BDS的PPP函数模型，式（12）、式（13）、式（17）、式（18）为GPS/BDS组合的PPP函数模型。组合PPP的未知参数包括3个测站位置、1个接收机钟差、1个系统偏差、1个对流层延迟和多个模糊度参数。

1.2 随机模型

给定先验单位权中误差σ0，则观测方程的权为：

值得注意的是，由于北斗GEO卫星的轨道和钟差精度较低[5]，为了获得高精度定位结果，在数据处理中应适当降低GEO卫星的权。

2 数据来源与处理软件

本文PPP数据处理采用自主研发的GNSS数据处理软件。该软件支持多频多系统数据处理，具备精密星历与钟差产品编辑、PPP、轨道积分与拟合等功能。我国南部地区更靠近赤道，因此电离层较北部地区活跃。本文采用南部地区的观测数据进行处理和分析，结果更具普适性。本文数据来源于我国南部沿海某工程的3座B级GNSS观测站（B001、B002和B003），站点分布如图1所示。3座测站的观测日期均为2019年第316—318天（年积日316-318），采样间隔为15 s，同时跟踪GPS与BDS卫星信号。3座测站均采用TRIMBLE接收机和天线，详细信息如表1所示。

图1 站点分布图

表1 测站观测设备信息表

数据处理时，GPS采用L1和L2双频信号，BDS采用B1和B3双频信号。由于BDS-3卫星保留了BDS-2卫星观测信号[14]，因此本文将BDS-2与BDS-3卫星进行等同联合处理（B001测站）。在PPP时，需已知精密星历和精密钟差产品，而观测期间IGS分析中心中仅武汉大学提供BDS-3卫星的精密星历和钟差产品（WUM），因此选用该分析中心产品进行PPP解算。

3 定位结果分析

本节主要对3座测站单天观测数据和2 h观测数据的GPS、BDS、GPS/BDS组合PPP定位结果进行分析，并对PPP计算的CGCS2000坐标精度进行评估。

3.1 单天观测数据

当测站具有多天观测数据时，受观测误差、模型误差以及其他已知数据误差的影响，不同天PPP结果会有差异。这种差异可作为评价单天PPP精度的指标之一，即多天PPP解的坐标重复性（自定义）：

式中，ci为各时段解的坐标分量；为相应分量的协方差；cˉ为相应坐标分量的加权平均值；R为相应的重复性。

3座测站均具有3 d观测数据，可获得3个单天PPP解。3座测站在3种处理模式下的单天PPP各坐标分量重复性如表2所示，可以看出，各测站在3种处理模式下各分量重复性均较好，平面分量（N、E）重复性小于5 mm，高程分量重复性小于1.5 cm；BDS高程分量重复性略差于GPS，这与目前仍没有精确的BDS接收机PCO与PCV校正模型有关；GPS/BDS组合解的平面重复性略有提高，高程重复性处于单GPS与单BDS之间。

表2单天PPP坐标分量重复性/cm

除坐标重复性外，GPS与BDS两种不同技术的PPP处理结果符合性也可作为评价PPP精度的指标。本文将各测站3 d的加权平均值作为最终结果，对比了3座测站GPS与BDS定位结果的差值，如表3所示，可以看出，3座测站平面坐标分量差值较小，除B003点的东西（E）分量超过1 cm外，其他均为毫米量级；3座测站平面坐标分量差值的平均值也为毫米量级；各测站高程分量符合性弱于平面，3座测站高程分量差值的平均值约为1.6 cm。

表3 GPS与BDS单天PPP结果差值/cm

由上述分析可知，无论是GPS、BDS还是GPS/BDS组合解的单天PPP精度均较高，平面可达毫米级，高程约为1～2 cm；无论是坐标重复性还是与GPS定位结果的差值，B001点的高程分量精度均明显优于B002点和B003点，其可能原因在于BDS-3卫星信号增强了星座几何结构。

3.2 2 h观测数据

本文将单天观测数据从UTC零点开始每隔2 h截取一段观测数据，每天可截取12段观测数据；分别对截取的观测数据进行PPP解算，得到2 h的PPP结果；再将GPS/BDS组合单天解加权平均值作为真值，通过比较2 h解与真值的差异，评价2 h解的定位精度。

3座测站第316天在GPS、BDS、GPS/BDS组合3种处理模式下2 h观测数据的PPP结果与真值的坐标差值均方根（RMS）所有时段的平均值如表4所示，可以看出，GPS、BDS单系统2 h观测数据的PPP精度平面分量一般小于4 cm，高程分量GPS小于5 cm，BDS较差约为7.5 cm，这可能与2 h时长的数据观测量不足有关；GPS/BDS组合解定位精度明显提高，各时段平均RMS平面分量小于2 cm，高程分量小于3 cm。受篇幅限制，本文仅展示了GPS/BDS组合PPP各时段定位结果的RMS（图2），可以看出，分时段解与时段无明显相关性，所有时段解的平面分量RMS均小于3 cm，高程分量除第10时段（19:00—20:00 UTC）略大于6 cm外，其他时段均小于5 cm。

表4 2 h观测数据的PPP结果时段平均RMS/cm

图2 GPS/BDS组合PPP各时段定位结果

3.3 CGCS2000坐标

我国目前已全面启用CGCS2000坐标系，评价PPP获得的CGCS2000坐标计算精度更具有实用性。本文PPP解算直接得到的是ITRF14框架、瞬时历元坐标，而CGCS2000采用的是ITRF97框架、2000.0历元。因此，对PPP解算结果进行框架转换和历元转换，可得到CGCS2000坐标。本文采用IERS的框架转换参数和由华南板块运动模型计算得到的测站速度场，获得了测站的CGCS2000坐标。

本文PPP计算得到的CGCS2000坐标（GPS/BDS组合单天解加权平均值）与已知坐标的坐标分量差值如表5所示，该差值主要由PPP计算的ITRF14框架下坐标误差、框架转换误差、历元转换误差和已知坐标误差引起，可以看出，PPP计算得到的CGCS2000坐标综合误差平面分量与高程分量均小于5 cm；3座测站N分量与E分量差值均成系统性，这主要由历元归算时测站速度场误差引起，证实了测站速度场精度对结果影响显著。

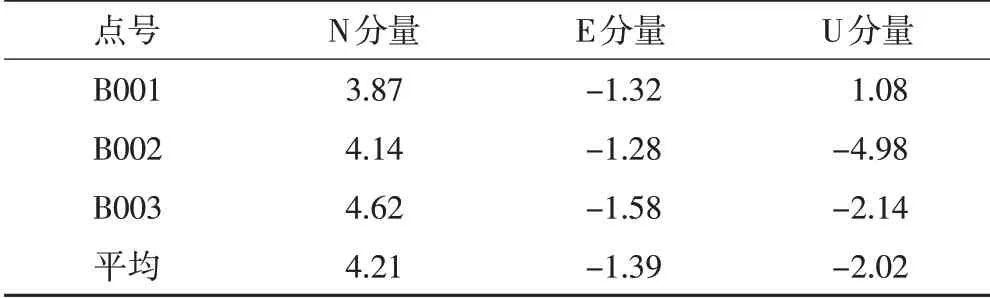
表5 PPP计算得到的CGCS2000坐标与已知坐标差值/cm

受限于板块运动模型计算的测站速度场精度，PPP计算得到的CGCS2000坐标精度低于ITRF14框架下的坐标精度。若能通过CORS站等方式得到更精确的测站速度场，则可进一步提高PPP获得的CGCS2000坐标解算精度。

4 结语

本文介绍了GPS/BDS组合PPP的数学模型，并采用GPS、BDS、GPS/BDS组合3种PPP处理模式对我国南部地区3座GNSS观测站数据进行了处理分析。结果表明，在ITRF框架下，单天解定位结果3种处理模式平面精度均可达毫米级，高程精度约为1～2 cm；2 h观测数据处理结果精度略差，GPS平面与高程精度均小于5 cm，BDS平面精度小于5 cm，高程精度约为7 cm，而GPS/BDS组合解精度明显提高，平面精度可达2 cm，高程精度为3 cm。PPP解转换至CGCS2000框架下的平面与高程坐标精度均小于5 cm。因此，在实际数据处理中，对于单天数据可采用单GPS、单BDS或GPS/BDS组合PPP结果；对于2 h或更短的观测数据，建议采用GPS/BDS组合定位。若应用中要求精度较高的CGCS2000坐标，则需获取精确的测站速度场以消除转换过程中的系统差。