一种汽车混流总装生产线排产的超启发式算法研究

卢梓扬，盛步云，王 辉，李晓芳

(1.武汉理工大学 机电工程学院,湖北 武汉 430070;2.湖北省数字制造重点实验室，湖北 武汉 430070;3.湖北航天技术研究院 计量测试技术研究所,湖北 孝感 432000)

随着汽车制造行业大规模定制化的演进，混合产品合理高效的产出排序能为车企削减成本。因此混合总装线排产是汽车企业制定生产计划的基础和关键点，它的优劣对整个汽车制造企业的生产周转有很大的影响[1-2]。在比较不同时间周期(月、季、年)、不同批次的生产数据(主要是工序完工时间等工时数据)后发现混流总装生产系统本身具有一致性、稳定性，而以往的研究大多聚焦在算法的性能上，没有对生产系统信息进行记忆学习，这样在处理不同的批次订单时，往往就是在解决一个全新的问题，造成了生产系统信息资源的浪费。因此笔者设计了一种以Q-learning强化学习为上层策略，GA(genetic algorithm)、DE(differential evolution)为LLH(low-level heuristics)(底层算法库)的超启发式算法，旨在结合不同算法优点，高效解决同一生产系统下的混流总装排产问题。

1 总装车间混流总装线模型分析

汽车混流总装线如图1所示，其排序问题通常可以描述为：有n辆汽车(T1，T2，…,Tm，…,Tn)需要在流水线上进行生产装配，在生产工艺流程确定的情况下，通过改变车辆的生产顺序，使得整个生产过程的目标最优化[3]。假设条件如下：①将分装线体产生的组件作为物料考虑，生产按一个流进行生产，传送带以速度vc运动，节拍为tc；②总装车间每个生产工位对于既定车型的生产时间为已知，不考虑设备损坏、人员休息等随机约束；③无限能力排产；④不允许过载操作，即操作工人在自己的工作域内不能完成作业任务就必须停线,直至完成后重新启动传送带[4]。

优化目标为：①车型切换调整费用最小化；②装配线空闲/停线时间最小化；③物料消耗均衡化[3,5]。

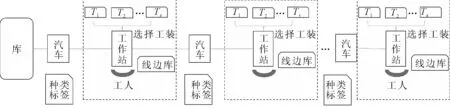
图1 混流总装线示意图

1.1 符号定义

混流总装车间调度问题模型中涉及的符号及定义如表1所示。

表1 符号定义表

1.2 目标函数

(1)车型切换装配线调整时间最小化目标f1。当第m位次车辆与第m-1位次车辆在Wn工位的工艺不相同时，工装的切换次数加1,表示为式(1)。v(Pmn,Pm-1,n)为已知的不同工艺间的切换费用系数，车型切换装配线调整时间最小化目标可以表示为式(2)[6]。

(1)

v(Fmn,Fm-1,n))

(2)

(2)装配线空闲/停线时间最小化目标函数f2。当工位工作在下一节拍开始时就被完成，则等待时间bmn为：

(3)

当在作业域内无法完成工作时，生产线停线时间SSmn直至工位任务完成，生产均衡化目标函数如式(4)所示，权重ω1取值0.87，ω2取值0.13。

(4)

更一般的有式(5)和式(6)。

(5)

Pmn=max{Pm-1,n+vcCm-1,n-Ln,0}

(6)

此时若m车发生超载停线，则此时(Pm,n+vcCmn-Ln)>0，由Omn(事件m型车在n号工位上加工)导致的停线时间SSmn由式(7)，Sm+1,n由式(8)，Pm+1,n由式(9)可得。

(7)

(8)

Pm+1,n=(vc·(Smn+Cmn-Sm+1,n))=

Ln-Pm,n-vctc

(9)

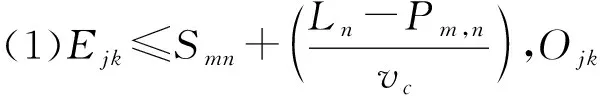
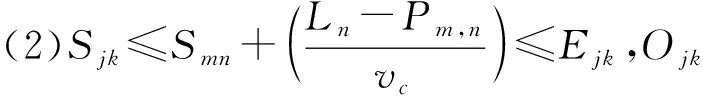
若RPTjk≤SSmm则有Pj+1,k=0;SSjk=0。

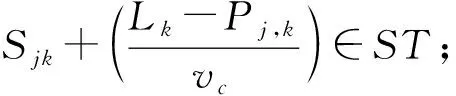
(10)

Pj+1,k=(vc·(Sjk+Cjk-SSmn-Sj+1,n))=

2Ln-Pj,k-vc(tc+Cmn)-Pm,n

(11)

特别的，若RPTjk>SSmn，且有Pi-1,j+vc(Cij+SSmn)-Ln≤0，则有Pj+1,k=0;SSjk=0。

(3)物料消耗均衡化目标函数f3[6]。设总物料为Q共有q种,CSin为车型i(i=1,2,…,M)在工位Wn的加工过程所需物料表，CSin=(bomin,P),其中bomin是CSin所需物料编码集合，bomin={Qr,…,Qr1}，Pinr是Qr类零件在该加工过程的数量，则CSin可由式(12)[6]确定。

(12)

一个投产批次内的M种车型对物料Qr(r=1,2,…,q)的需求量RNi可由车型数量di(i=1,2,…,M)和车型i(i=1,2,…,M)所需物料Qr(r=1,2,…,q)的数量Pinr计算出。

(13)

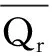
(14)

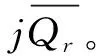
(15)

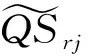
(16)

则优化目标f3为：

(17)

(4)整体目标函数f。多目标函数优化问题求其帕累托前沿是复杂的，而单纯使用经验权重因子法，其解空间不一定能覆盖最优解，因此笔者采用先求解帕累托前沿的一个子集Q再设置k1,k2,k3的值的方式，使得式(18)的解空间R与Q存在关系∀α∈Q,∃β∈R,α=β。

f=k1f1+k2f2+k3f3

(18)

2 基于Q-learning算法的总体设计

笔者采用Q-learning作为高层策略，建立包含GA和DE的LLH(低层算法库)，依据LHH构建action表。在每次迭代后，以评估函数的值为依据，选择最有潜力的搜索策略[7-9]。基于Q-learning的算法流程如图2所示，步骤参见表2。

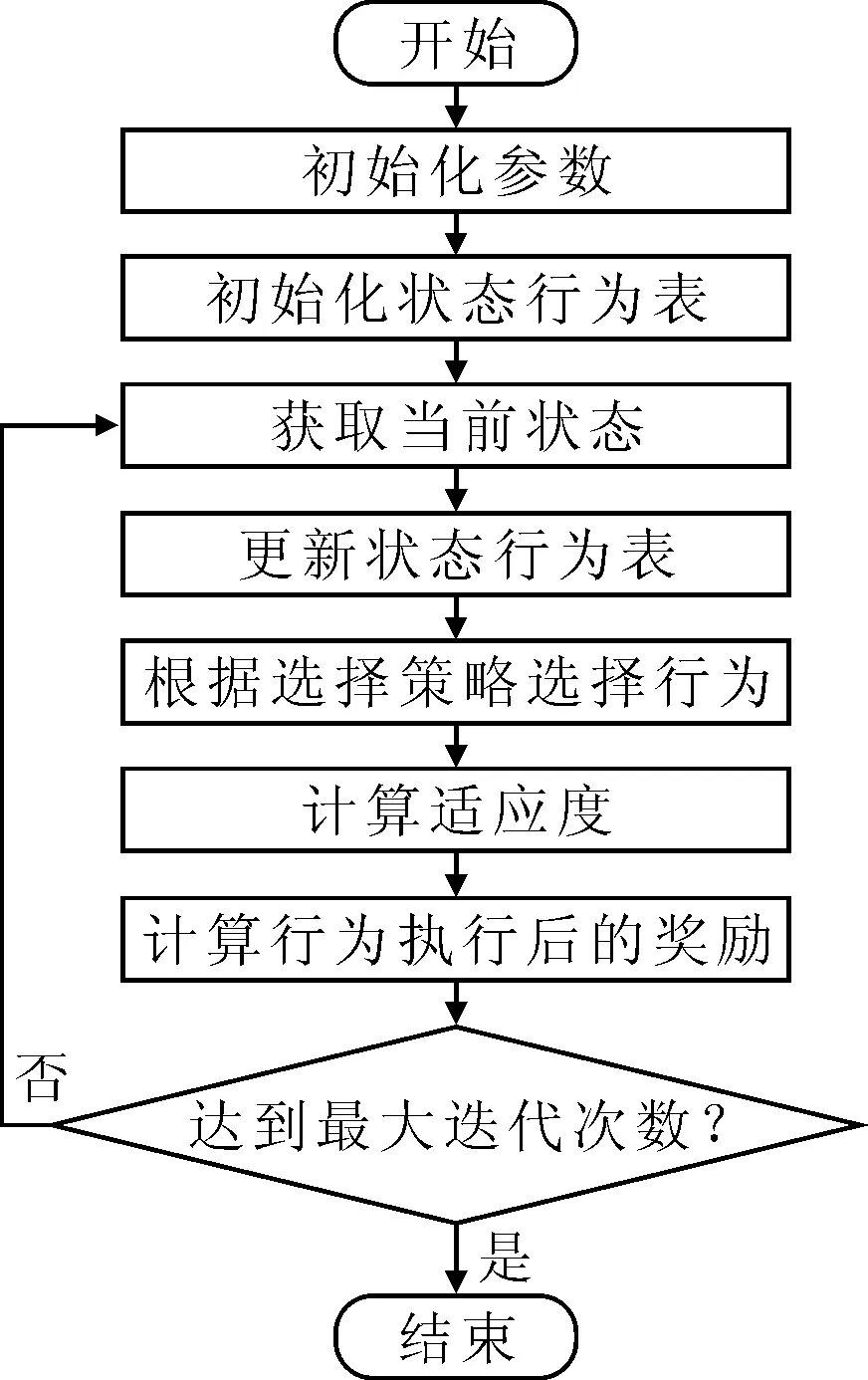
图2 Q-learning算法流程图

表2 Q-learning算法步骤表

2.1 染色体编码

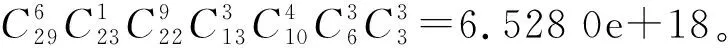
若采用常规编码方式如整数编码则解空间大小为829=1.547 4e+26，相差了8个数量级严重滞后了寻优速度。因此笔者利用排列组合本身的性质设计了一种染色体-基因编码方式，如图3所示。该染色体包含两个基因，基因A中含有的信息划分方案是对车型数量P的划分方式，以可空方式将P辆车划分到x+1个空位中。基因B中是将划分方案填充到空位的方式以整数编码表示。这样在进行交叉、变异操作时，能够保证生成的新个体仍然在解空间中。

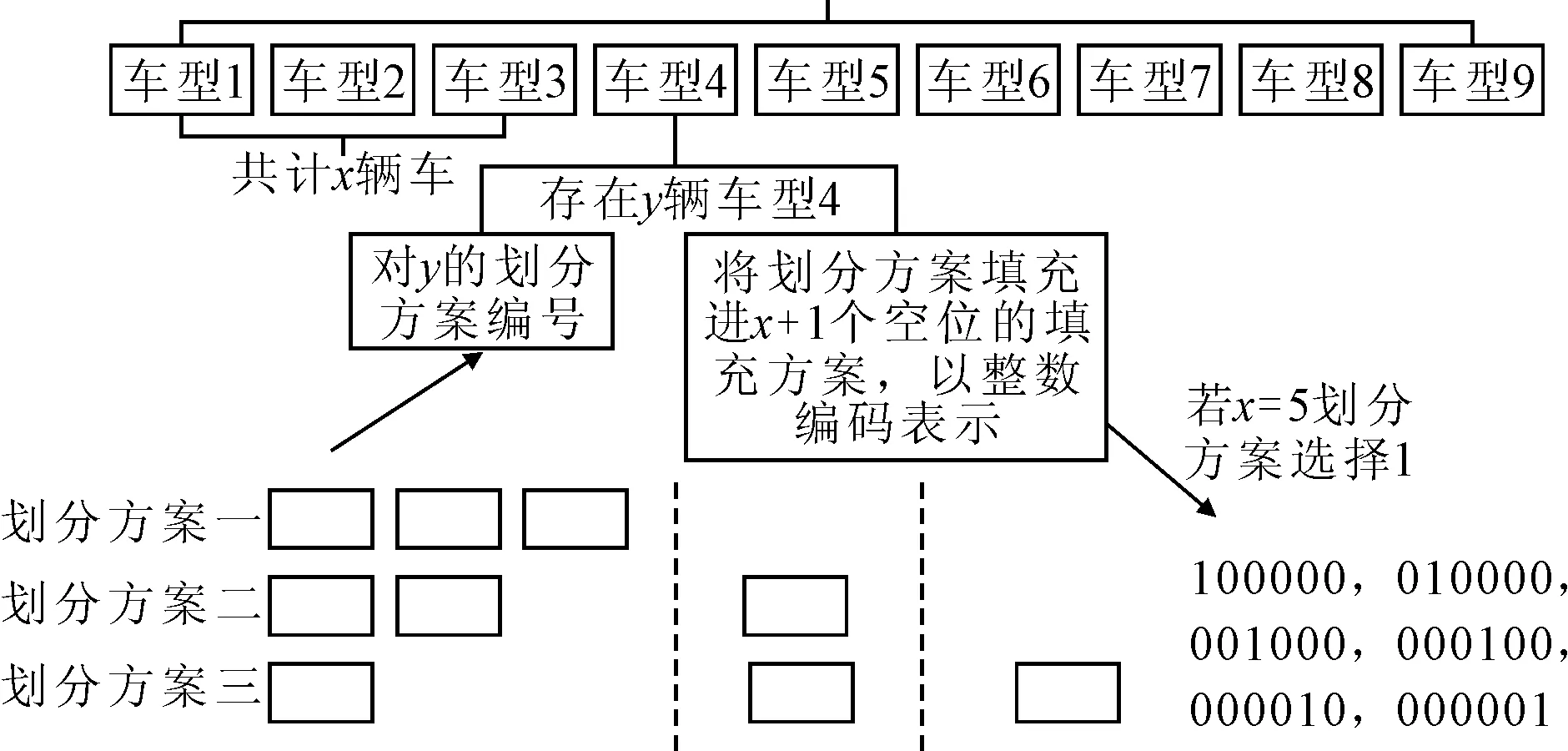
图3 个体编码方式图

2.2 状态描述

状态是Q-learning算法中agent所理解的一种环境特征，agent需要借助这种环境特征，同最佳行为建立起稳固的联系，从而作为一种有价值的经验而得到存储。状态平均偏差率fa1可由式(19)和式(20)描述，即每次迭代后解的目标值的平均偏差，如果偏离值较低，说明产生的相似解较多，后续迭代将趋向于收敛；如果偏离值较高，表示解的差异性较大，算法正在进行积极的全局搜索。

(19)

(20)

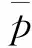
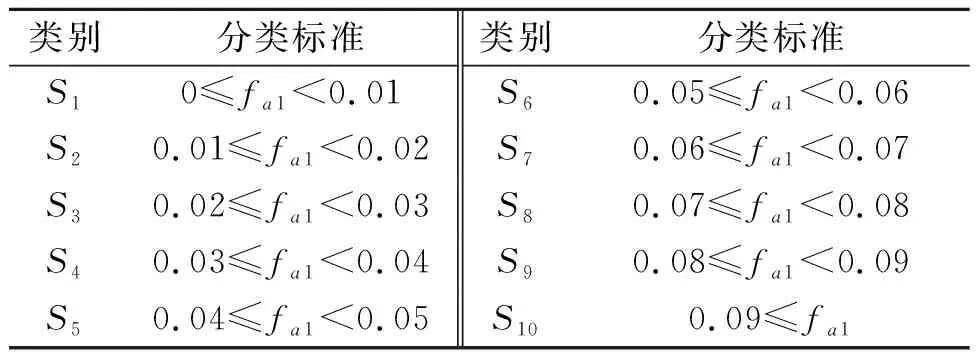
表3 状态分类表

2.3 行为定义

行为是Q-learning算法对当前状态环境做出的响应。充分迭代后，agent会趋向于选择对当前状态环境而言未来回报最高的行为[10]。通过GA和DE两种算法的不同算子进行组合，从而获得4种搜索方法，即Q-learning的4种行为，如表4所示。

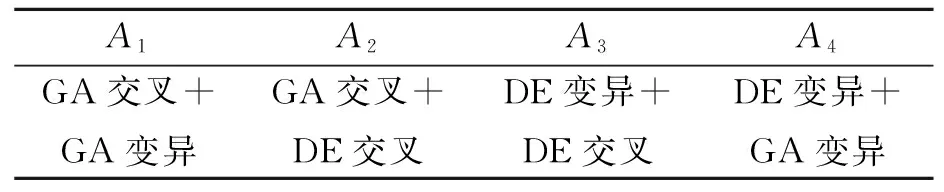
表4 4种行为表

2.4 行为选择策略

在迭代初期，尝试尽量多的选择有助于agent学习到更多的历史经验，也有助于避免算法陷入局部最优。为避免算法过早地收敛，采用随机轮盘赌策略，选择概率P(Si,Ai)公式如下：

(21)

式中：Q(Sj,Ai)为每一对状态Sj和动作Ai的奖励期望值。

采用选择概率P(Sj,Ai)来选择每一候选行为Ai(i=1,2,……,NA)，其中NA为行为的数目。

2.5 行为奖励及Q值更新

行为奖励将巩固agent对当前行为A(l)决策的记忆，并且在下次遇到相似状态时，agent将会以更高的概率选择同一行为。将本次迭代结果同历史最优结果的比较结果作为行为奖励的依据，若当前迭代结果优于历史最优结果，则设置奖励值r(l)=2，否则r(l)=0。更新Q值矩阵意味着对当前环境的行为决策经验进行记录，也是对历史经验的再更新。通过Q-learning的学习机制，每一对状态-行为Q(S(l-1),A(l-1))的Q值矩阵将由式(22)得到更新：

Q(S(l-1),A(l-1))=(Q-α)(S(l-1),A(l-1))+

(22)

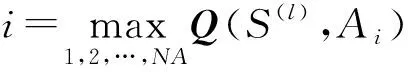
2.6 适应度函数

适应度函数都是由目标函数转化而来，适应度函数由式(18)表示。

3 算例结果与分析

以某汽车生产排产计划为算例，对所提出的总装车间混流排产模型及基于Q-learning的超启发式算法的求解进行验证。该算例拥有30个批次订单、包含T1、T2、T3、T44种车型配置，及100种物料，进行总装装配的有10个工位。Q-learning算法、GA算法和DE算法的参数设置如表5～表7所示，不同迭代次数统计结果如表8所示。

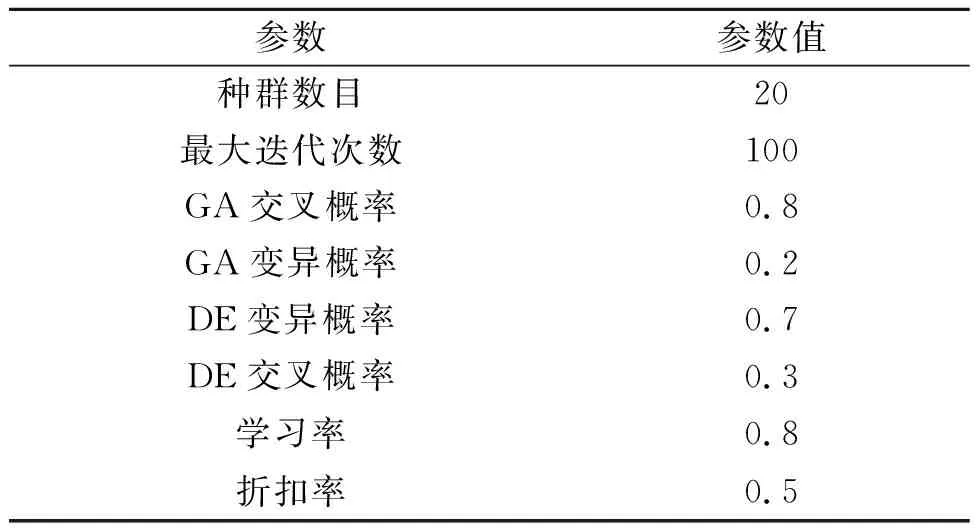
表5 Q-learning算法的参数设置表

表6 GA参数设置表

表7 DE参数设置表

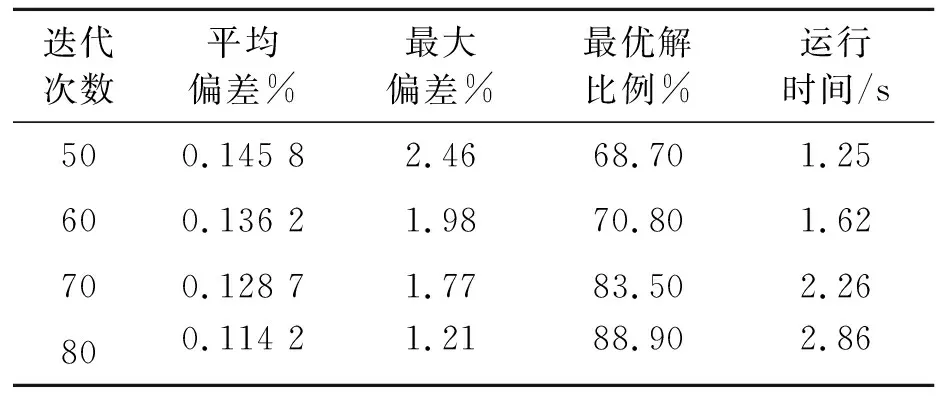
表8 不同迭代次数统计结果表

在求解质量方面，将 30个批次订单随机划分为训练组20个和对照组10个，利用随机选取订单的策略训练Q-learning超启发式算法1 500次。同时观察Q矩阵的值，当其趋于稳定后，对对照组的10个订单进行各10次求解并与标准GA算法和DE算法进行对照比较，结果如表9所示。通过对比可知，综合考虑平均偏差、最大偏差、优解比例，本文所提算法性能有明显提升。

表9 本文算法与标准GA、DE比较表

4 结论

实现基于现场混流车间的排产是一项庞大复杂的工程，所涉及的领域多、约束多、例外情况多。笔者聚焦于混流生产线排产，合理地建立了目标模型，通过问题特性分析建立实用的染色体编码方式，通过基于学习的超启发式算法有效地结合不同启发式算法提高了对同一系统下不同订单的收敛速度。