考虑设备退化和不完美维护的柔性作业车间集成调度
王 磊,闻 婧,刘 依,孙利波
(1.武汉理工大学 机电工程学院,湖北 武汉 430070;2.湖北省数字制造重点实验室,湖北 武汉430070;3.武汉东湖学院 机电工程学院,湖北 武汉430299;4.天津水泥工业设计研究院有限公司,天津 300400)
生产调度和设备预防性维护(preventive maintenance,PM)是影响加工生产的两项重要技术。生产调度是指在满足工艺约束和设备可用的条件下合理安排加工计划,以缩短工期和降低成本。PM是保障设备可靠运行和加工过程可靠的技术决策和管理手段,通过PM提高设备可靠性至关重要[1],但在标准车间调度问题中一般假定设备持续可用。实际上,设备长期运行会退化,役龄随之增大、可靠度降低,进而导致停机或生产出缺陷产品而带来巨大的损失成本。因此在制定生产计划时,需要将设备维护考虑进去,将车间调度与设备维护进行集成调度决策。
预防性维护活动一方面可以降低故障发生的频次,另一方面也会占用加工时间。目前,有研究者根据该问题提出了相应的解决方法。Chen[2]等考虑了具有不同效果的维护活动,并提出改进遗传算法求解模型。Ye[3]等基于机器实际役龄引入修正系数以动态更新预防性维护间隔。Khatami等[4]提出了连续维修活动之间的间隔和每台设备上的维修活动数为非固定的协调生产和维修调度模型。其中,针对柔性作业车间调度问题,Zandieh[5]等考虑生产过程中机器不可用的情况,进行了基于状态的维修仿真,提出了改进的帝国竞争算法求解模型。李聪波[6]等建立了面向能耗的柔性作业车间预防性维护的混合役龄模型。Li[7]等使用来自制造执行系统的历史数据预测维护任务的相关参数并提出基于可靠度和成本的生产计划与预防性维护的集成方法。
上述文献对考虑设备维护的车间调度问题进行了系统研究,大多数的维护策略是将当前状态与可靠度阈值相比来决定是否维护。假设设备初始役龄为0,维护可以使设备恢复如初也并不符合实际情况,该方式难以保证设备在加工每一个工件的可靠度始终维持在阈值以上。
笔者的研究对象为某液压件制造企业机械加工车间,目前车间的维护方式为参照说明书和凭借经验定期对设备实施预防性维护措施,存在设备可靠性不足,在实际生产中频繁发生报修、修理的状况。因此提出动态安排维护活动的策略,设备当前是否维护取决于加工完下一工件时的可靠度,同时考虑了设备退化效应以及不完美维护的情况,在决策中兼顾生产部门和设备部门的需求,以最小化最大完工时间和维护成本为优化目标,依据实际情况针对不同设备设置了相应的可靠度阈值及不同的维护参数,设计了改进的混合人工蜂群算法来求解模型,解决生产过程中生产调度与设备维护不协调的问题。
1 集成调度模型
1.1 符号说明
为了方便讨论,引入数学符号如表1所示。

表1 符号定义表
决策变量如下:
(1)
(2)
1.2 问题描述
柔性作业车间调度问题可以描述为:有n个工件在m台设备上加工,每个工件有j道工序,j道工序之间有加工先后约束,不同工件之间没有工艺约束。每台设备一次只能加工一道工序,工序一旦进行就不能中断。
本文研究的集成优化问题为:确定每道工序的加工设备以及每台设备维护活动的开始/完成时刻。具体步骤如下:
步骤1在每一个初始解中将各台设备的加工序列分离出来,得到在该设备上加工的工序及其加工顺序;
步骤2每安排一道工序之前,计算设备i加工完这道工序后的可靠度,如果低于阈值,则在加工前进行设备的预防性维护,同时更新维护后设备的有效役龄及可靠度,直到设备i上的所有工序完成安排;
步骤3在每台设备上重复步骤2,直到所有工序和PM都被安排。
1.3 数学模型
在集成模型中需要考虑故障发生的规律以及预防性维护活动和退化效应给设备带来的改变。实际生产中,设备的故障服从威布尔分布λ(t),如式(3)所示。
λ(t)=(β/η)×(t/η)β-1
(3)
式中:β为形状参数;η为长度参数,可由历史数据统计获得;t为设备的役龄。
威布尔分布对应的可靠度函数R(t)为:
R(t)=exp[-(t/η)β]
(4)
为避免故障发生需要对设备采取主动预防性维护措施。PM只能使设备性能回到介于新旧两种状态之间,属于不完美维护。引用文献[8]提出的改善因子来量化PM对设备役龄的改变。
(5)
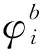
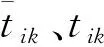
(6)
(7)
设备i在加工完第k个位置上的工件后可靠度Dik为:
Dik= exp(-(tik/η)β)
(8)
设备在不断的生产加工过程中会逐渐磨损导致设备退化从而实际加工时间增长,工序在设备i上的实际加工时间uijh为:
uijh=pijh+δi·pijh
(9)
δi为设备i的退化因子, 计算公式为:
δi=tik/Tpmi×δ
(10)
对于集成调度问题,既要生产尽快完工,又要在保证设备可靠度的前提下降低维护成本,因此设定优化目标为完工时间和维护成本最小,其数学模型为:
(1)目标函数:
f=min(Ctmax,Cost)
(11)
(2)约束条件:
Ctmax=maxCj
(12)
(13)
(14)
(15)
Cj(h-1)≤Sjh
(16)
Ti(k-1)≤Bik
(17)
(18)
(19)
(20)

(21)
式(11)表示最大完工时间和总维护成本最小;式(12)表示最大完工时间是所有工序中最迟结束加工的时间;式(13)为总维护成本;式(14)~式(17)分别为每一工件的先后次序约束;式(18)表示每台设备中每个加工位置一次只能分配给一个工件;式(19)表示每个待加工工件的同一道工序只能分配到一台设备上加工;式(20)表示设备待加工工序的总数与待加工工件的工序总数相等;式(21)表示维护策略,设备i在加工第k个工件前执行预防性维护与否和第k个位置工件完工时的可靠度有关,如果第k个位置的工件完工时小于可靠度阈值Dpmi,则yi(k-1)=1,执行预防性维护;否则yi(k-1)=0,不执行预防性维护,直接处理下一个工件。
2 算法设计
人工蜂群算法(artificial bee colony algorithm, ABC)行为简单、控制变量较少且易实现,然而它在算法后期搜索效率较低[9]。笔者在跟随蜂阶段引入模拟退火算法以避免陷入局部最优,并针对模型的双目标结合了快速非支配原则,提出了混合人工蜂群算法。算法整体流程如图1所示。
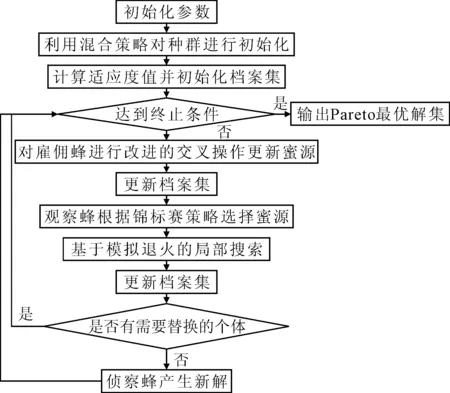
图1 算法流程图
2.1 编码和解码
生产部分包括确定任务的加工顺序和设备的选择,维护部分包括为预防性维护活动安排位置。根据问题特点设计4层编码方式,分别是工件编码(JV)、工序编码(OV)、设备编码(MV)和维护编码(PV),每层编码长度均为工序总数。个体的编码方式如图2所示。JV中每个数字表示工件号;OV中表示与JV相对应工件的工序;MV表示相应工序所选的设备;PV确定工序加工前是否需要维护,若维护,则是1,否则为0。

图2 编码方式
解码时根据前3层编码确定加工顺序和使用的设备,根据第4层编码插入维护活动及对应的维护时间。
2.2 蜜源初始化
初始解的优劣影响收敛速度和最终解的质量,笔者采用随机生成与策略选择相结合的方式来生成初始蜜源。①工序的分配规则:ⓐ随机选择,使工序随机排序;ⓑ工序剩余最多规则,找出存在未加工最多的工序进行加工。②设备的分配规则:ⓐ随机选择规则:在设备集中随机选择一台设备来处理工序;ⓑ加工时间最小规则:将工件的工序分配到能在最短时间内完成该工序的设备上加工。 采用混合策略进行种群初始化,经过实验验证当规则混合比例为ⓐ50%、ⓑ50%的时候能获得较好的结果,种群分散的同时质量也得以保证。
前3层编码初始化完成后,根据各工件工序在各自设备上的加工顺序,将加工后的役龄带入式(4)计算可靠度并与其阈值比较,低于阈值则表明加工该工序前需要维护。至此,4层编码初始化完成。
2.3 档案集的维护和更新
多目标优化算法的求解目标是找到一个具有代表性的非支配帕累托解,将初始化种群后所有的非支配解共同组成Pareto档案集,采用固定容量的档案集可以保证非支配的多样性。档案集维护和更新步骤的伪代码如下[10]:
档案集生成机制
输入初始种群P
fori=1 toNgen#Ngen最大迭代次数
搜索过程中产生新的个体pnewi
Ifpnewi不是非支配解
pnewi不能添加到D
Else ifpnewi是非支配解且D容量剩余
pnewi添加到D
Else ifpnewi是非支配解且D已满
将pnewi加入到D重新计算所有个体拥挤距离并将距离最小的个体移除
End if
香菇 性平、味甘,具有益气健脾、解毒润燥等功效,香菇中含有的多糖类物质,可以提高人体的免疫力和排毒能力,抑制癌细胞的生长,增强机体的抗癌能力。香菇还能降低血压、降低胆固醇、预防动脉硬化,并有强心保肝、宁神定志、增强人体新陈代谢及促进体内废物排泄等作用。
End for
输出D
2.4 雇佣蜂
为了增强算法的搜索能力,采用交叉的方法对雇佣蜂搜索操作进行改进。具体步骤如下:①产生一个随机数r,0 图3 交叉操作示意图 经过交叉操作后会产生一些不可行解,结合种群初始化的方法对余下3层编码进行修正。若此时子代优于父代,则用该子代来代替父代。 在跟随蜂阶段采用锦标赛选择方法,当跟随蜂选择策略都完成后,每只跟随蜂执行基于模拟退火的局部搜索。伪代码如下: 跟随蜂阶段局部搜索 输入初始解S={S1,S2,…,Sse} j←1 Begin While (j 运用模拟退火算法产生新的食物源Snew IfSnew优于Si Sj=Snew Else j=j+1 End while 输出S End 侦察蜂操作能提高种群的多样性。传统ABC在侦察蜂阶段通过随机产生新解的方式来避免算法陷入局部最优,笔者采用档案集替换策略,具体操作过程的伪代码如下: 侦察蜂阶段更新机制 输入种群P={p1,p2,…,pN} 输入D={D1,D2,…,Dsize} #档案集 找出P中更新次数超过限制次数最多的个体的索引k fori=1 toN Ifpi与pk不相等 生成一个不大于档案集容量的随机数r pi=Dr#从档案集中随机挑选出一个个体 End if End for 以某液压件制造企业的机械加工车间为例,每道工序可选择的设备集如表2所示,对应加工时间如表3所示。每台设备的历史维护数据来自现实制造车间,如表4所示。实验参数如表5所示。 表2 候选设备集 表3 加工时间 工时 表4 6台设备的相关数据 集成优化方案(方案一)即笔者所提出的在制定生产调度计划时还考虑了设备维护活动所占用的加工时间,每安排一次维护活动都会对接下来的生产任务进行相应调整。独立决策维护是生产部门和设备部门各自制定其调度和维护方案,有基于可靠度阈值的独立决策(方案二)和基于固定周期的独立决策维护(方案三),均是先按照传统的FJSP(flexible job-sjop scheduling problem)调度方式得到生产计划,再通过计算工序完工时的可靠度来判断设备是否需要维护,或每间隔一段固定时间就对设备实施预防性维护活动,独立决策的加工顺序一旦确定就不再发生改变,不具备依据实际情况进行调整的动态性。 表5 实验参数 引用文献[8],假设式(5)中的成本调节系数a=1,时间调节系数b=0.007,学习效应调节系数ω=-0.355。代入cai、cpi,可求出设备i的预防性维护改善因子。方案一的调度甘特图如图4所示,实体部分为维护时间段,相应地计算出该方案下的总维护成本。并将改进的ABC与标准ABC和粒子群算法(particle swarm optimization,PSO)进行对比,PSO算法除了没有档案集维护环节,其余部分均与改进ABC相同,结果如表6所示。 图4 方案一调度甘特图 表6 改进ABC与其他算法结果对比 为了进一步验证所提策略的有效性,对不同规模下的问题进行测试,取工件数量分别为10、20、30、50,其余实验参数同上。结果如表7所示。 表7 不同工件数量下的结果比较 通过3种方案对比表明,在保证设备可靠度的前提下,集成调度要优于独立决策。 以柔性作业车间调度问题为研究背景提出了一种车间调度与设备维护集成优化的方法,采用动态安排维护活动的策略,即设备当前是否维护取决于加工完下一工件时的可靠度,在模型中考虑了设备退化和不完美维护的情况,改进了编码方式和初始化方法,并且在跟随蜂阶段加入模拟退火算法来提升算法在邻域的搜索能力和防止算法陷入局部最优。通过与传统维护策略对比,验证了本文模型和算法的有效性。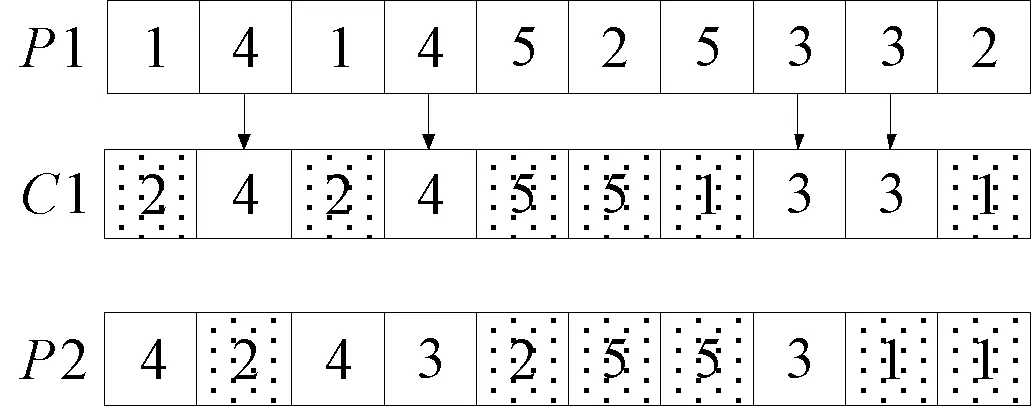
2.5 跟随蜂
2.6 侦察蜂
3 案例分析
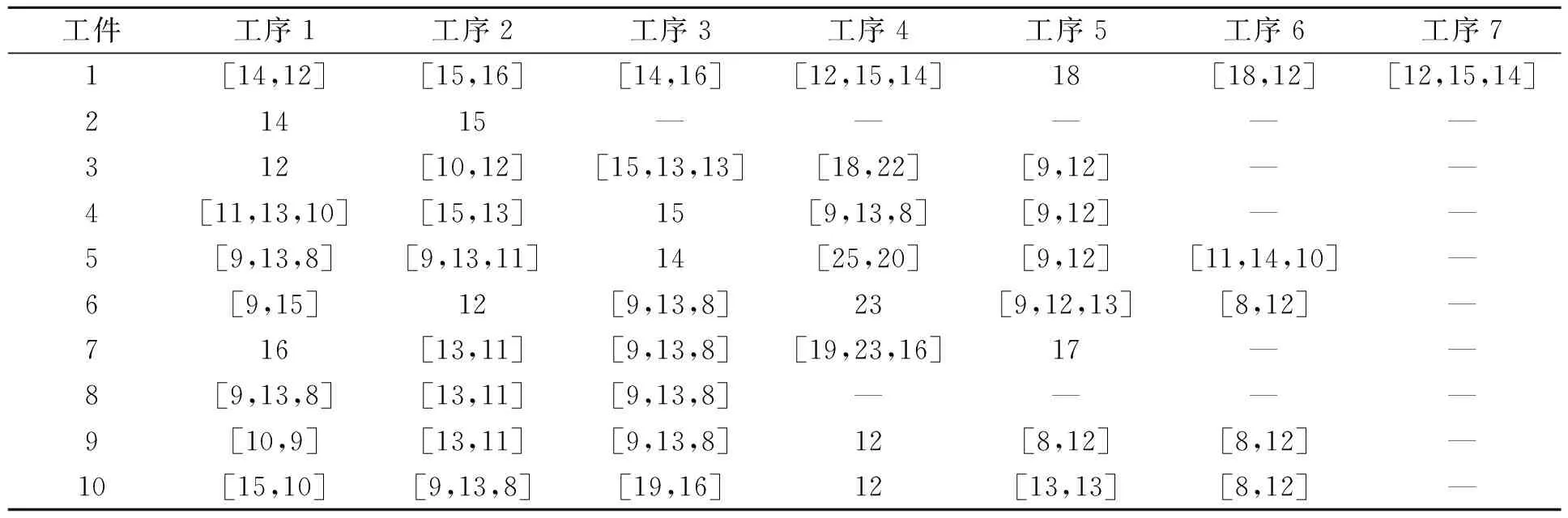
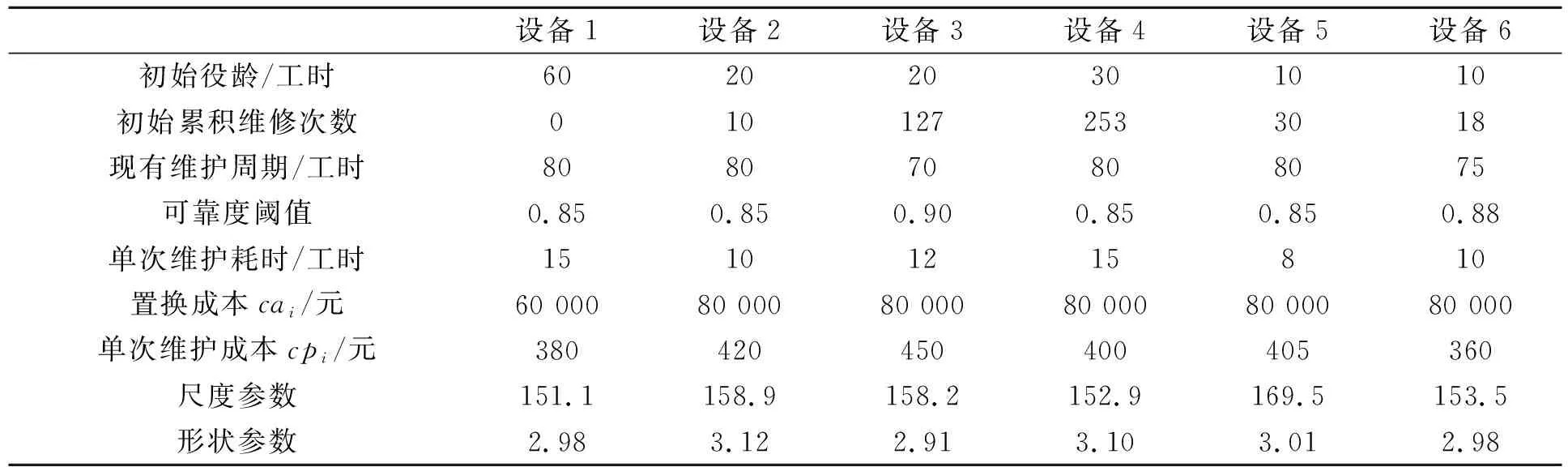
3.1 测试算例与实验参数

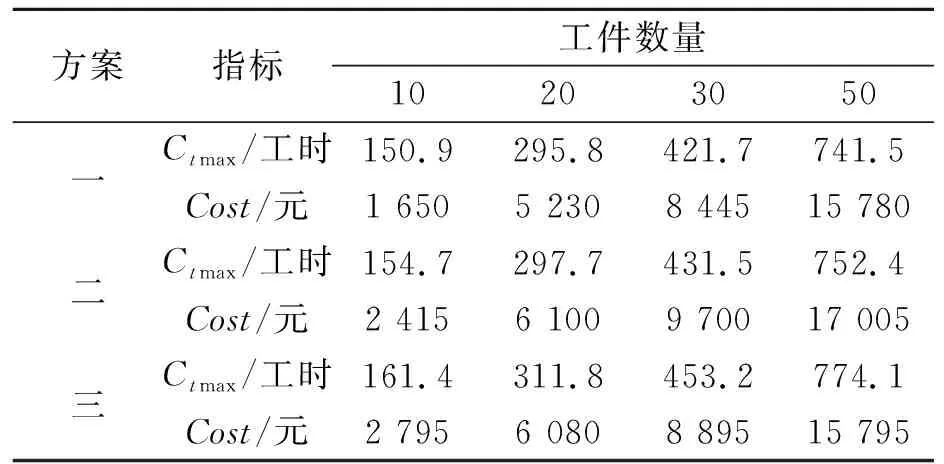
3.2 实验结果



4 结论

