多品种小批量模式下离散制造车间调度问题研究

唐红涛，杨 源，闻 婧

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2.湖北省数字制造重点实验室，湖北 武汉 430070)

离散制造是现代制造的重要组成部分，也是国民经济的重要支柱。离散制造企业大多采用面向订单生产(make-to-order，MTO)的经营模式，这使得离散制造具备多品种、小批量的特点，并且各订单之间的技术标准不同，导致无法成批生产，离散制造车间的生产管控更为复杂[1-2]，研究离散制造车间的生产调度问题对提高国家整体的制造水平有着重要意义。

国内外学者对以作业车间和流水车间为代表的离散制造车间生产调度问题展开了大量研究，取得了较为丰硕的成果[3-5]。Qiao[6]等针对离散制造车间高污染问题，建立了以最小化生产总成本和碳排放量为目标的生产调度模型，并使用改进的遗传算法求解该问题。宋昌兴[7]等研究了准备时间不确定的混合流水车间调度问题，建立了一个以最小化总拖期和制造期的多目标优化模型，针对模型特点，基于NEH(nawaz ensore ham)-Pareto对传统的模拟退火算法进行改进，最后的仿真实验证明了算法的优越性。

车间调度问题属于典型的NP(nondeterninistic polynomin)-Hard问题[8]，而多品种模式下的柔性流水车间调度问题是在流水车间的基础上考虑的多品种生产特性，故其仍然属于NP-Hard问题范畴。诸如遗传算法(genetic algorithm, GA)[9]、粒子群算法(partical swarm optimization, PSO)[10]、灰狼算法、蛙跳算法[11]等智能优化算法等具备较快的求解速度，常被用于车间调度问题。特别地，候鸟优化算法(migrating birds optimization algorithm，MBO)是一种新兴的群智能优化算法，其具备参数少，求解质量高等特点，近年来也被逐渐地被运用于求解车间调度问题。

大多数参考文献将多品种-小批量模式下的调度问题处理为批调度问题，将同一类产品作为一个整体或者看作是一个工件进行批量调度，其本质上仍然属于单件调度问题，不能实现更为精细化的调度方案。因此，笔者以柔性流水车间为研究对象，建立了一个多品种小批量模式下的生产调度模型，针对该模型的特点，设计了一种改进的候鸟优化算法求解该模型，并构建了多组适用于多品种小批量模式下的混合流水车间调度问题的测试算例，通过与多个算法对比，验证了改进的候鸟算法的高效性。

1 问题描述及模型构建

1.1 问题描述

以离散制造车间的典型代表柔性流水车间为例，多品种模式下的柔性流水车间调度问题(multi-variable flexible flow-shop scheduling problem，MFFSP)可描述为：车间需生产I种类型的产品，每类产品的生产批量为Ni，每件产品互不影响，所有产品都需要经过n个加工阶段的处理，每个加工阶段至少有一台并行加工的设备可供选择，每台设备的加工时间不完全相同。MFFSP的目标为：为每件产品安排合适的设备并确定所有产品在设备上的加工顺序以及对应的开工和完工时间，使得某个调度指标如总完工时间、设备负载率等最小等。

所研究的多品种模式下柔性流水车间调度问题主要解决以下两个问题：①为每件产品分配加工设备；②确定每件产品的开工时间和完工时间。

为便于研究，笔者基于如下假设构建数学模型：

(1)在0时刻，所有的产品和设备均可用；

(2)产品投入生产不会被中止；

(3)同一时刻，一台设备只能加工一件产品；

(4)同一时刻，任一产品只能被一台设备加工；

(5)所有产品均有相同的工艺路线；

(6)不考虑设备故障、物料短缺等意外事件；

(7)所有产品的加工时间已知且固定，忽略各道工序间的运输时间。

1.2 模型构建

1.2.1Y 符号与参数

I：产品的类型数量；

i,s：产品的类型编号，i,s∈[1,I];

Ni：第i类产品的工件总数量；

Ns：第s类产品的工件总数量；

j,t：工件标号，j∈[1,Ni]，t∈[1,Ns];

pij：产品种类i中的第j个工件;

n：产品的加工阶段总数，即产品的最后一道工序编号;

k：工件的加工阶段编号，k=1,2,…,n;

Mk：第k阶段的设备数量;

mkl：加工第k阶段的设备中的第l台设备，l=1,2,…,Mk;

Qkl：设备mkl所加工的工件数量；

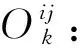
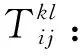
R：一个无穷大的正数;

Cij：工件pij的完工时间;

Cmax：所有工件的完工时间最大者。

1.2.2 决策变量

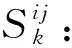
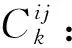
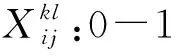
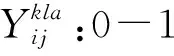
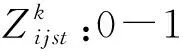
1.2.3 目标函数

minCmax=max{Cij} ∀i,j

(1)

(2)

(3)

1.2.4 约束条件

(4)

k∈[1,n];l∈[1,Mk]

(5)

j∈[1,Ni];t∈[1,Ns];k∈[1,n]

(6)

j∈[1,Ni];t∈[1,Ns];k∈[1,n]

(7)

(8)

(9)

式(4)为每个工件的每个加工阶段只能选择一台设备进行加工；式(5)为一个工件在一台设备上只允许加工一次；式(6)和式(7)为同一阶段不同工件存在先后加工顺序次序约束；式(8)为同一工件不同阶段存在先后顺序约束；(9)为决策变量的取值范围。

2 改进候鸟算法求解调度模型

2.1 基本候鸟算法简介

候鸟算法MBO是由Duman于2012年提出的一种群智能算法，适用于诸如车间调度等离散优化问题，该算法的灵感源于候鸟迁徙行为。MBO算法包含种群初始化、领飞鸟进化、跟飞鸟进化、领飞鸟更新4个步骤，种群初始化形成V形队列，处于队列最前端的领飞鸟对自身执行邻域搜索完成进化，左、右两队列前端的两只跟飞鸟除了对自身进行邻域搜索外还会保留来自领飞鸟的邻域解，这有利于增强算法的全局搜索能力，如此循环多次后，从左右两个队列中随机选取一只跟飞鸟替代领飞鸟，原来的领飞鸟放至队列的尾部，循环迭代多次完成整个算法的流程。

2.2 编码与解码

笔者采用基于产品类别编号的单层编码方式，如X=[2,3,2,3,1]表示工件第一个阶段的加工顺序，X是由产品类别编号组成的一个序列，其元素出现的次序为该类产品的工件编号，如X序列中处于位序3上的元素2第2次出现，表示第2类产品的第2个工件(用P22表示)，X序列对应的工件加工顺序(第一个阶段)为：P21-P31-P22-P32-P11。

上述编码方案相对于双层编码方式而言，解空间减少一半且能解决多品种工件排序问题，但其仅表示工件第一个阶段的加工顺序，后续阶段的工件排序以及设备分配需要通过解码机制获取，本文采用的解码机制如下：

但是，EPC总包模式也不是完美的。智慧物流园区建设不同于传统的园区信息化建设。首先，智慧物流园区更加强调的是站在园区的顶层视角，统筹考虑园区信息化发展需求和推进路径，而不是孤立狭隘的建设一个个项目；其次，园区的信息化建设仅仅是智慧物流园区建设工作的一部分，建设完成后不等于能够用好，要能够让智慧物流园区可持续的运转起来，建设的项目能够产生预期以及持续的效益，这才是智慧物流园区发展的最终目标。

(1)后续阶段的工件排序。对于后续加工阶段(k≥2)，工件排序采用先到先加工(first in first out, FIFO)规则，即上一阶段中，工件完工时间更短者优先安排加工，若存在多个工件可供选择，从中随机选取一个工件优先安排加工。

(2)设备分配规则。设备分配采用最早完工优先(the earliest completion time first, ECTF)规则，首先通过上述编码序列X可解码得到工件的加工顺序，按照该顺序依次为工件分配设备，工件优先选择能更早完工的设备，当存在多台设备可供选择时，优先选择加工时间最短的设备，若存在多台加工时间相同的设备，则随机选择。

2.3 基于反向学习的种群初始化

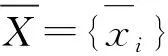
(10)

式中：xmin、xmax为X序列的上界与下界。

基于反向学习和随机的种群初始化步骤为：

步骤1随机生成种群规模为N的初始种群Pop；

步骤2从初始种群Pop中随机选取[N/2]([·]表示向上取整)个个体构成子种群Pop1，剩余的种群Pop2，按照式(10)对Pop1种群生成反向种群Pop3；

步骤3若反向序列所表示的解优于当前解，则替换，否则保留至种群Pop3；

步骤4合并Pop2与Pop3以构成新的种群。

2.4 邻域结构

领飞鸟进化与跟飞鸟进化均依赖于个体自身产生的邻域解，因此设计合理的邻域结构是MBO算法的关键步骤。对于车间调度问题，基于交换和插入操作的邻域结构较为有效，为进一步提高MBO算法的效率，对交换和插入操作进行改进，提出了最优交换和最优插入操作。

(1)最优交换操作。以n维度序列X={xi,1≤i≤n}为例，序列X为当前解，从X中随机选取一个位置r(1≤r≤n)，按照从左到右的顺序，将元素xr与其余n-1个位置的元素依次交换，比较交换后的邻域解与当前解的优劣，若优于当前解，则替换当前解并终止交换操作。

(2)最优插入操作。同样以序列X为例，从X中随机选取一个位置s(1≤s≤n)，将元素xs按从左到右的顺序插入到其余位置处，被插入位置及其后面所有元素均先后移一位，显然可以产生n-1个邻域解，当邻域解优于当前解时，则替换当前解并终止插入操作。

领飞鸟与跟飞鸟均使用最优交换操作和最优插入操作完成进化，进化过程中最优交换和最优插入执行机率各占一半。

2.5 局部搜索策略

为避免MBO算法陷入局部最优，对候鸟个体进行局部搜索，基于4种邻域结构对候鸟个体进行变领域搜索，4种邻域结构分别为：

(1)随机交换。从当前候鸟序列随机选取两个不同的位置，交换两个位置的元素形成新的邻域解。

(2)随机插入。从当前候鸟序列中随机选取一个位置，将该位置元素随机插入到其他任意一个位置形成新的邻域解。

(3)逆序操作。从当前候鸟序列中任意选取两个位置，将这两个位置之间的元素进行逆序操作，从而获得新的邻域解。

(4)打乱互换。从当前候鸟序列中随机选取多个位置，随机打乱这些位置上的元素顺序以获得新的领域解。

设集合C为包含上述4种邻域结构的集合，i为指向C中邻域结构的索引，X为候鸟个体，Ci(X)为使用集合C中的第i个邻域结构对个体X产生邻域解，基于上述4种邻域结构的变邻域搜索步骤如下：

步骤1初始化索引i，令i=1;

步骤2获取新的邻域解X*，X*=Ci(X)，若X*优于X，则用X*替换X，否则，令i=i+1；

步骤3若i≤4，执行步骤2，否则，结束变领域搜索，输出解X。

2.6 改进候鸟算法流程

在改进候鸟算法中各变量的含义如下：I为算法总迭代次数；i为当前迭代次数；Pop为候鸟种群规模；N为候鸟产生的领域解数量；g为领飞鸟与跟飞鸟巡回次数索引；G为最大巡回次数；x为领飞鸟未使用的领域解；l为左边队列跟飞鸟的索引；r为右边队列跟飞鸟的索引。

步骤1初始化算法参数(I，Pop，N，G)，令g=1，i=1；

步骤2使用反向学习策略完成种群初始化，种群中的第一只候鸟为领飞鸟，种群中第2只候鸟至第(P-1)/2只候鸟构成左队列，并令l=2，种群中第(P-1)/2+1只候鸟至第P只候鸟构成右队列，并令r=(P-1)/2+1；

步骤3领飞鸟进化。使用2.4中的邻域结构对领飞鸟生成N个邻域解，若最优的邻域解优于领飞鸟，则替换领飞鸟，并将领飞鸟未使用的x个邻域解分别传递至第l和第r只跟飞鸟；

步骤4若l≤(P-1)/2，则使用2.4中的邻域结构对第l只跟飞鸟(左队列)产生N-x个邻域解，若最优的邻域解优于当前跟飞鸟，则替换该跟飞鸟，并将未使用的邻域解传递给第l+1只跟飞鸟，令l=l+1，并继续执行步骤4；

步骤5若r≤P，则使用2.4中的邻域结构对第r只跟飞鸟产生N-x个邻域解，若最优邻域解优于当前跟飞鸟，则替换该跟飞鸟，并将未使用的邻域解传递给第r+1只跟飞鸟，令r=r+1且g=g+1，并继续执行步骤5；

步骤6若g≤G，跳转至步骤2，否则执行步骤7；

步骤7对候鸟种群进行局部搜索；

步骤8随机选择左队列或者右队列中的第一只跟飞鸟替换领飞鸟，并将当前领飞鸟置于对应队列的末端，令i=i+1；

步骤9若i>I，算法终止，否则，跳转到步骤2。

3 仿真实验

3.1 实验设计

为验证IMBO(improved migrating birds optimization)算法求解MFFSP模型的性能，将IMBO算法与遗传算法(GA)、离散粒子群算法(discrete particle swarm optimization, DPSO)以及经典的MBO算法进行对比实验，对比算法的参数均按照相应参考文献建议值设置，笔者所提IMBO算法采用正交试验法经过多次组合试验获得：候鸟种群规模P=60，最大迭代次数I=200，候鸟产生邻域解数量N=5，传至下一只候鸟的邻域解数量x=2，候鸟进化最大巡回次数G=10。所有算法均采用上述编解码方式，IMBO采用基于反向学习的种群初始化方式，其他算法均采用随机初始化方式。使用Matlab 2016b软件编写，运行在Intel Core i7、CPU 2.9 GHz、RAM 8 GB、Window 10的64bit计算机上。同时为了保证实验的公平性以及避免实验结果的偶然性，每个算法独立运行20次。

3.2 算例构建

笔者基于Benchmark算例集[4]构建适用于多品种小批量模式下的柔性混合流水车间调度问题测试算例，具体的构建参数如表1所示，产品类型数量分别为5、10、15和20，加工阶段数分别为5、10、15，故可构建12个测试算例，算例的命名规则为“产品种类数-加工阶段数”；阶段数为5和15的测试算例采用参考文献[4]中提出的c类设备布局(中间阶段有2台设备，其余阶段均为3台设备)，阶段数为10的测试算例采用d类布局(所有阶段均有3台设备)，每类产品的生产数量xi为区间[1,5]上服从离散均匀分布的随机数，加工时间为区间[10,20]上服从离散均匀分布的随机数。

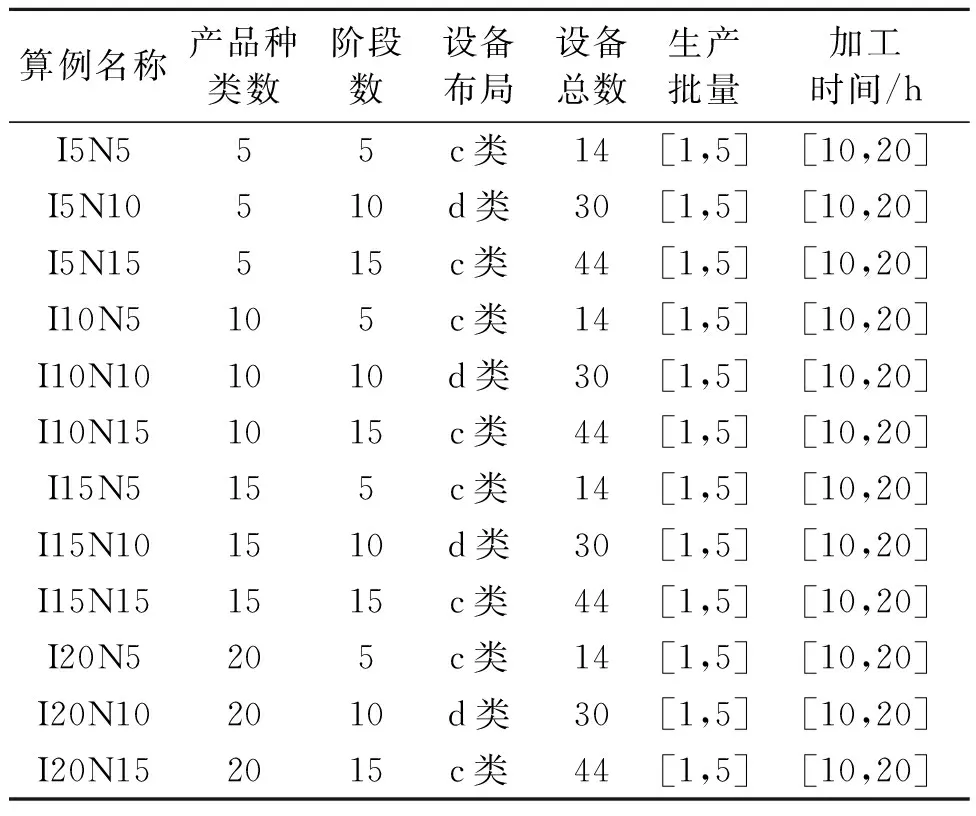
表1 算例构建参数

3.3 结果分析

基于上述构建的12个算例开展算法对比实验，采用最优值(Cbest)、最差值(Cworst)、平均值(AVG)以及相对误差(RPD)4个指标对算法结果进行评价，式(11)为RPD的计算公式，其中，C0为当前算法运行20次的最优值，C1为所有算法运行20次的最优值，实验结果如表2所示。

(11)

从表2可知，IMBO在最优值方面取得了11个算例的最优解，对应的RPD值均为0；在最差值方面取得了11个算例的最优解，对应PRD值只有算例I5N10为1.15，其他算例均为0；在平均值方面取得了10个算例的最优解，RPD值均为0，这证明了IMBO算法的可行性和稳定性，MBO在寻优能力上不及IMBO，这是因为所提出的IMBO增加了变邻域局部搜索的原因，极大地提升了MBO的寻优能力，GA算法和DPSO算法性能相差不大，但寻优能力和稳定性均远落后于IMBO算法。图1给出了算例“I10N15”的迭代曲线图，显然，IMBO算法的寻优能力最强，其中的局部搜索极大避免了算法陷入局部最优，其相对于其他3种算法而言，IMBO算法具有更快的收敛速度。

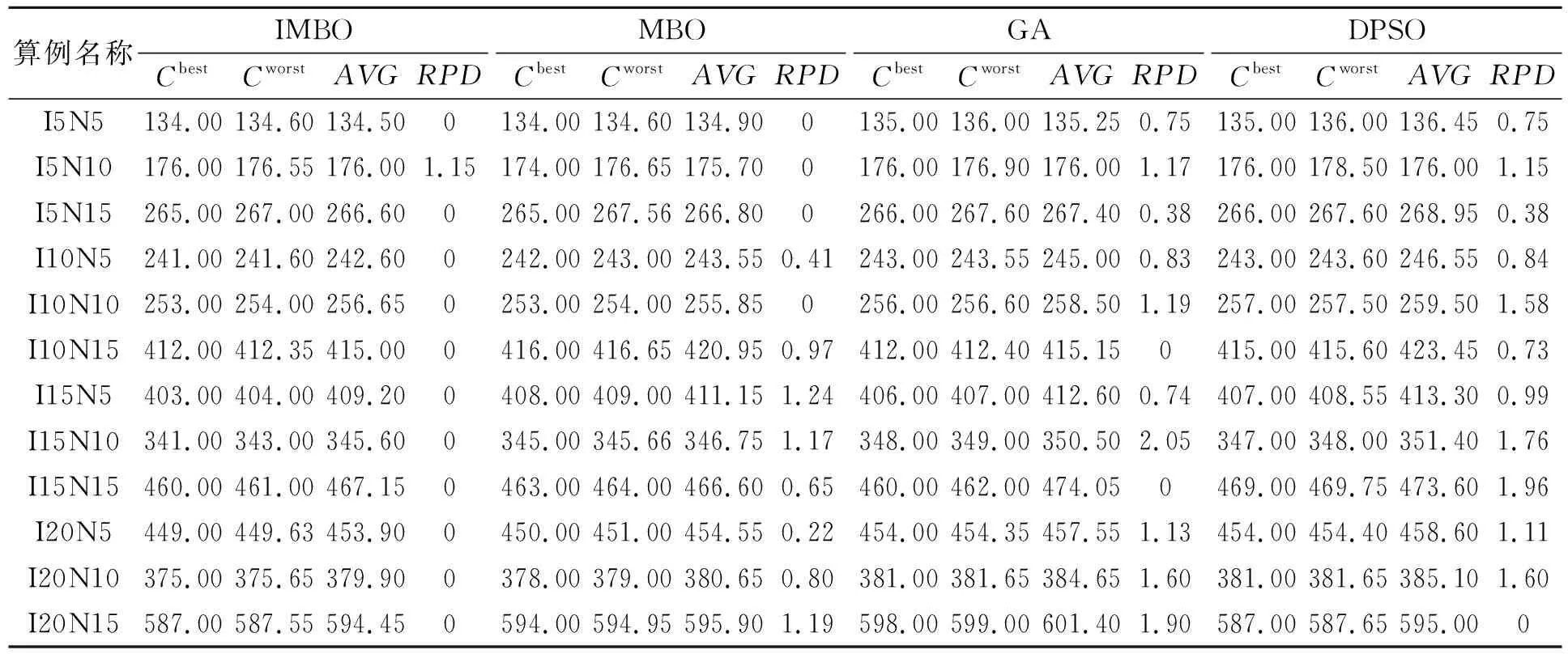
表2 算法对比结果

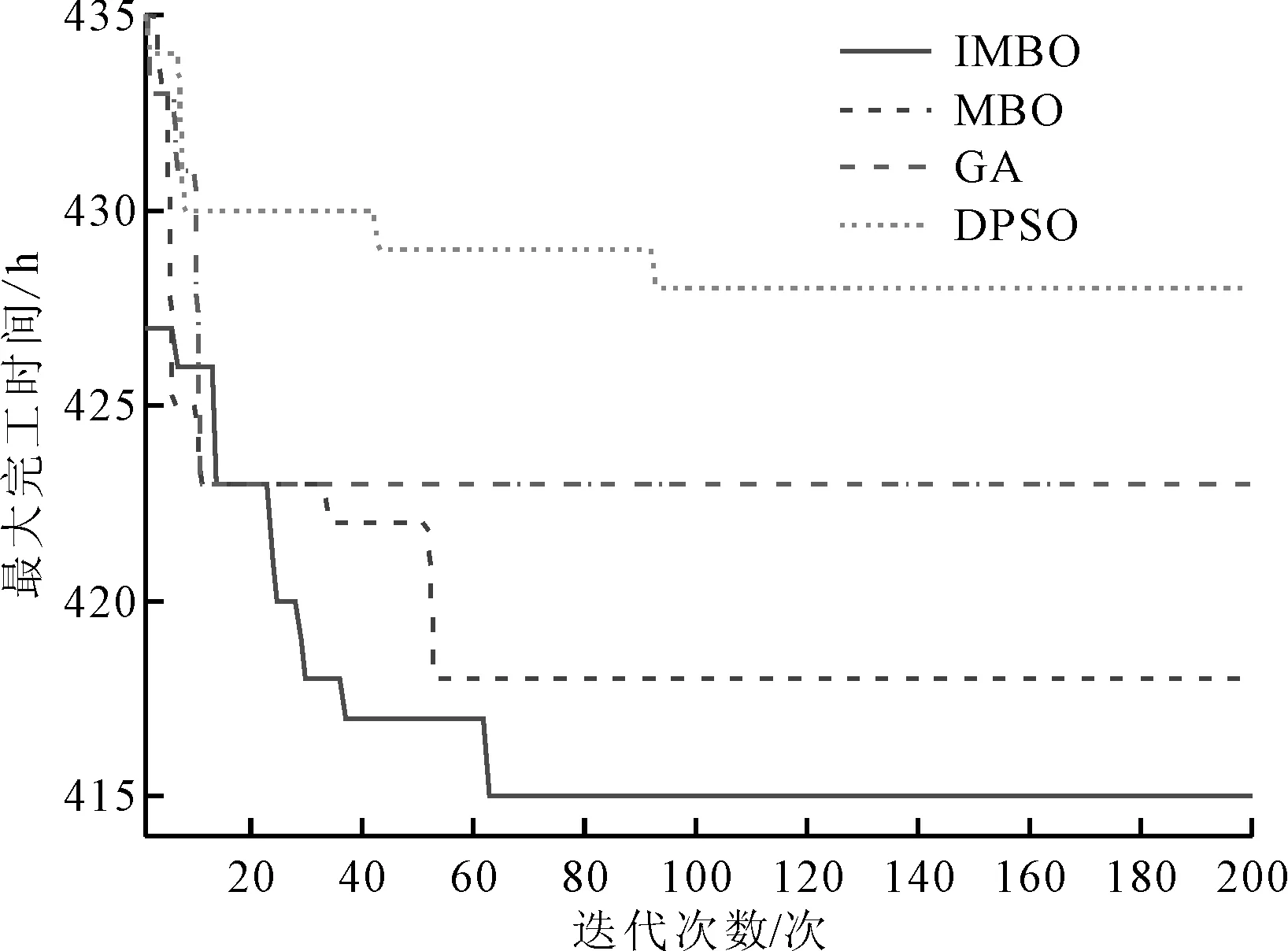
图1 算例I10N15的迭代曲线图

4 结论

笔者研究了多品种、小批量模式下的柔性流水车间调度问题，建立了以最小化最大完工时间为优化目标的数学模型，针对多品种小批量的生产特点，对传统的MBO算法进行改进，基于Benchmark算例集构建了12个适用于该模型的算例，并设计了对比实验，证明了IMBO算法的有效性及高效性。