非线性混沌网络系统的分散性能量子优化算法

王晓晗

(咸阳师范学院 数学与信息科学学院,陕西 咸阳 712000)

0 引 言

依据量子力学理论[1]发展出的量子算法,由于其具有高并行性的特点,目前已开始在智能控制、神经网络等方面发挥重要作用。但因为量子算法提出时间较短,其理论依然处于初级阶段[2]。

为提升量子算法的应用性能,量子优化算法的研究成为一个热门研究方向。叶青等[3]提出以协同决策方法为核心的集成优化模型,计算量子种群内个体权重,以此为基础,建立优化激励策略。并且通过设置合理的学习阈值,避免出现局部最优解问题。但该方法全局搜索效率较低。薛文等[4]针对整个量子种群进行分析,将其按照PSO(Particle Swarm Optimization)算法和混沌机制划分为两个种群,分别进行迭代处理。针对两个量子种群进行交叉迭代处理,计算量子适应值并进行排序,完成全局极值的更新,实现量子优化算法的全局优化。但该算法的收敛效率较低。曾明华等[5]按照布谷鸟算法搜索量子行为,结合模拟退火原则,设计了一种改进的优化算法。为增强优化算法的全局寻优能力,针对布谷鸟搜索设计动态步长飞行方案,保证量子优化结果的多样性。但该方法寻优能力较差。

为此,笔者参考传统量子优化算法,提出以非线性混沌网络系统为基础的优化算法。混沌网络内包含众多节点,使所提出的量子优化算法具有局部分散控制特点,利用非线性混沌网络子系统控制局部信息,更加快速地完成量子优化处理。

1 非线性混沌网络系统的分散性能量子优化算法设计

1.1 量子位置的混沌初始化

笔者优化算法以非线性混沌网络系统为基础,考虑到混沌具有非线性运动状态,将其遍历性特点应用于优化算法中,加强量子优化算法的全局搜索性能。为保证混沌搜索在优化算法中顺利应用,采用Logistic混沌映射方法[6],计算分散性能量子的初始化混沌位置。

通过分段Logistic混沌映射建立混沌序列,以此确定初始化量子所处位置,在确保优化算法的随机性不受影响的同时,加强全局最优搜索的遍历性,量子混沌映射序列表示为

(1)

其中i表示量子,i=1,2,…,m,m表示量子总数,zi表示量子混沌映射序列,μ表示控制参量。

根据研究可知,当控制参量为4时,Logistic处于完全混沌状态,与常规的混沌映射结果相比,该状态下混沌序列具有良好的分布对称性。应用完全混沌状态下的混沌序列,可更加准确地得到量子初始化位置。

针对混沌序列的敏感性特点,分析初始量子初值,将待优化的量子初值代入式(1),设置合理的迭代次数得到多个混沌序列。映射每个量子混沌分量,利用定义域区间内映射的混沌变量,计算量子初始化混沌位置

θi=ri(2zi-1)

(2)

其中θi表示量子初始化位置,(-ri,ri)表示量子混沌映射的定义域区间。

1.2 量子种群进化模式构建

根据上述计算,得到分散性能量子初始化位置后,经多次迭代计算得到每个量子个体的适应度值,依托于适应度值将待优化的量子群划分为顶层和底层种群,二者分别具有局部搜索和全局搜索的能力。

顶层量子种群的进化,通常情况下会表现出停滞状态。笔者针对该情况进行扰动变异处理,实现优化算法的局部搜索能力提高[7]。此外,选取底层量子种群内适应度较低的量子,通过混沌变异方式扩展量子优化搜索空间,达到提升优化结果多样性的目的。

其中顶层种群扰动变异处理的前提是判断量子种群停滞性,本质上是分析种群内量子是否出现“聚集”现象,当量子聚集程度较高时,就会出现迭代停滞问题。笔者通过群体适应度方差计算量子聚集程度,得到种群停滞性判断结果的同时,不会对量子分散性能优化算法的收敛速度产生负面影响[8]。群体适应度方差计算公式为

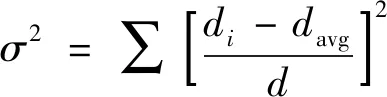
(3)

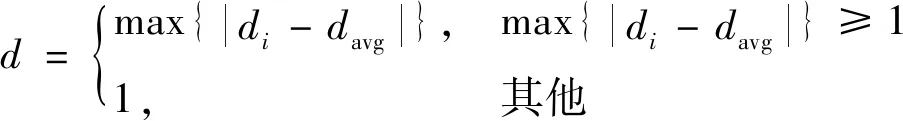
(4)

其中σ表示群体适应度方差,di表示量子适应度,davg表示当前量子群平均适应度,d表示归一化因子。但式(3)计算结果低于预先设置的阈值,代表当前量子聚集较为密集,当前迭代出现停滞。

种群停滞问题会造成量子优化结果出现局部最优化,笔者针对每个维度的全局极值添加高斯扰动,促进粒子优化结果避免局部极值点,高斯扰动添加后表达公式为

Pgi=Pgi+εR

(5)

其中ε表示扰动系数,R表示均值和方差分别为0和1的随机数,P表示量子种群,g表示全局极值维度。根据式(5)计算结果可知,高斯扰动的添加有助于优化算法的应用性能提升。

针对底层种群,为有效增大最优解搜索空间,将变异概率应用于分段Logistic混沌映射中,得到均匀分布的量子。量子优化过程中,需要预先确定搜索区域,笔者为避免收敛速度受到负面影响,设置混沌搜索区域半径为

L=S|pg-pi|

(6)

其中S表示比例系数,pg表示全局极值,pi表示量子个体极值,混沌搜索区域半径同全局极值和变异粒子之间的联系如图1所示。

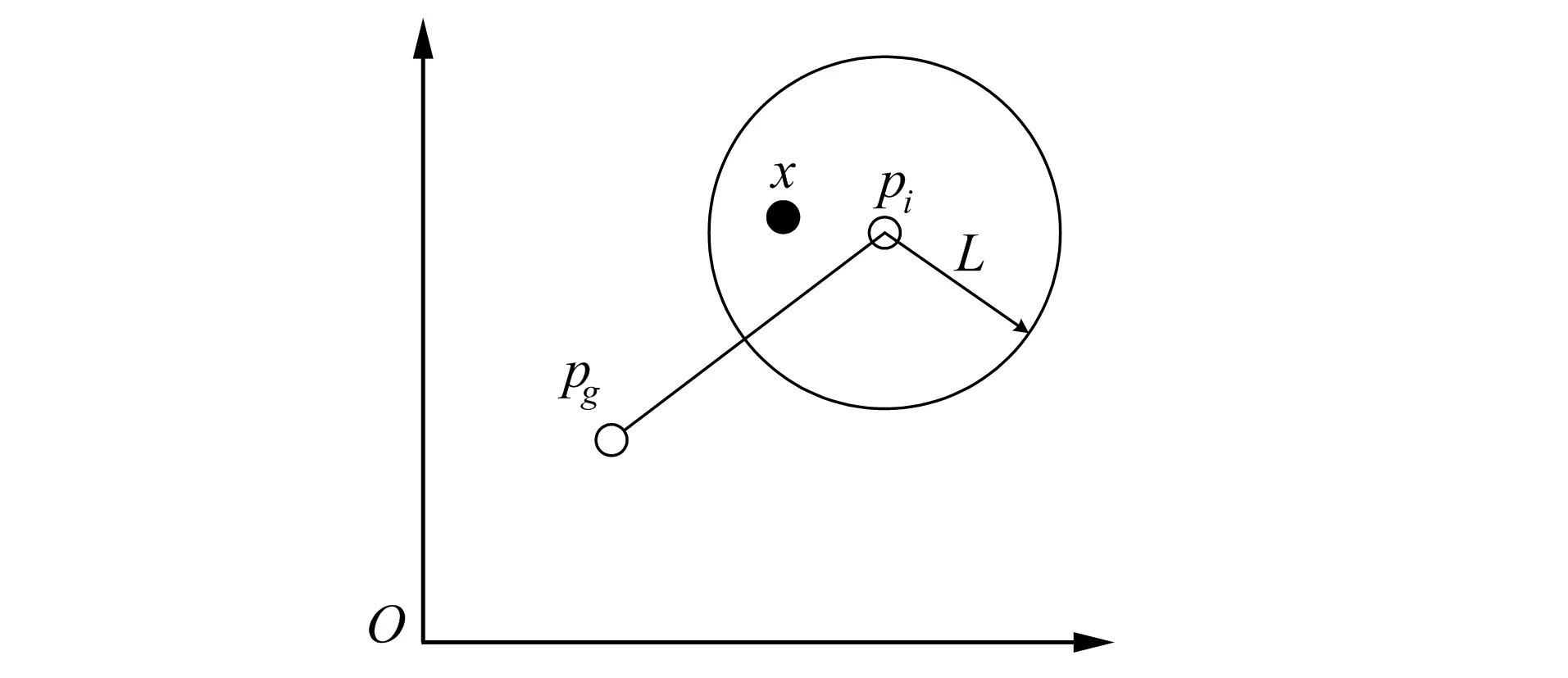
图1 影响半径和全局极值的变异粒子关系图Fig.1 Variation particle relationship between influence radius and global extreme value

根据图1可知,采用分段Logistic混沌映射模式生成的混沌序列内包含的变异量子,即为需要进行混沌变异处理的量子,按照量子所处维度,得到变异量子位置计算公式

(7)

1.3 非线性混沌优化控制方法设计

笔者针对量子的优化处理,设计以非线性混沌网络系统为核心的优化控制方法[9]。采用多个连续时间子系统,形成网络系统如下

βλ=ηλ(aλ,uλ),λ=1,2,…,N

(8)

其中N表示非线性连续时间子系统数量,λ表示子系统,aλ表示子系统状态,uλ表示子系统输入值,ηλ表示光滑系数,βλ表示非线性混沌网络系统。

参考线性化原理,可针对非线性混沌网络系统内平衡点,分析平衡点附近局部区域的稳定性。当平衡点附近的线性近似评估结果具有较强的稳定性,表明非线性混沌网络系统内具有局部稳定平衡点。根据非线性混沌网络系统的局部稳定性,生成最优化控制方法,确保闭环系统内混沌行为。

(9)

其中a*表示子系统内一个固定点,T表示非线性连续时间。假设子系统邻域内包含一个混沌吸引子,则可将子系统内的局部线性化系统表示为

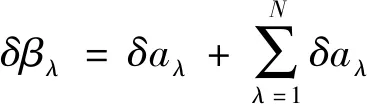
(10)

其中δ表示局部线性化系统。针对每个子系统进行分析,设置目标函数为

(11)

其中J表示子系统目标函数,∞表示正无穷,Q表示任意正定对称矩阵。采用非线性混沌网络系统控制分散性的量子优化时,目标函数计算结果越小,表明优化算法的收敛速度越快。因此,可以在量子优化过程中寻找最佳控制方案。

在子系统内随机选取两个局部线性化系统,结合最优控制理论,得出代数Riccati方程对称正定解计算公式

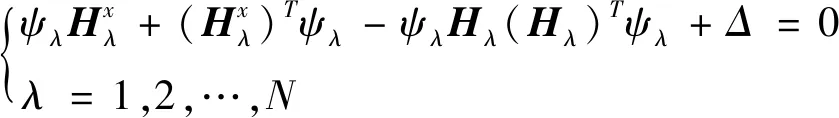
(12)

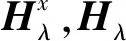
(13)

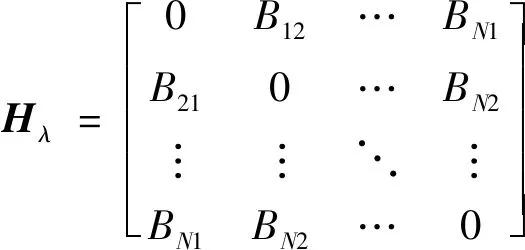
(14)

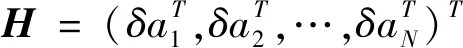
(15)

综合式(13)～式(15),可得出具有分散性能的非线性混沌优化控制公式

∂=KH

(16)

其中∂表示控制参数,K表示最优化函数。

1.4 分散性能量子优化实现

非线性混沌优化控制方法运行时,当某一个量子确定一点为最优解,其他量子会向该点聚集,表现出局部最优现象。针对该问题,采用早熟收敛判断机制,帮助量子种群避开局部最优点[10]。判断机制的设计,主要包括预防早熟收敛、处理早熟收敛两个环节,将两个环节相连接,运用于优化算法中,早熟收敛判断机制整体框架如图2所示。

图2 早熟收敛预防与处理框架图Fig.2 Framework diagram of premature convergence prevention and treatment

根据图2可知,早熟收敛判断结果是早熟处理的核心。经过分析可知,早熟收敛与全局收敛两种现象的出现,都会造成量子群内个体量子出现“聚集”问题。因此,笔者将早熟收敛判断的约束条件设置为量子最佳位置状态。再结合式(3)与式(4)进行计算,得到量子的“聚集”程度。选定一个合理的常数充当判断阈值,当计算结果低于判断阈值时,进行早熟处理。

考虑笔者设计的优化算法以非线性混沌网络系统为基础,针对早熟收敛问题运用混沌搜索技术进行处理。运用混沌搜索技术重复进行多次搜索,得到最优解位置,并将其作为量子全局最优位置,引导量子跳出局部最优点。通过混沌搜索处理模式,提升量子优化算法的收敛速度,完成量子优化计算。

2 实验分析

2.1 实验设计

为验证分散性能量子优化算法的实际应用效果,笔者引用一个测试函数进行优化处理,明确所提优化算法的应用优势。该实验所采用的测试函数为

(17)

其中f(x)表示测试函数,sin表示正弦函数。将测试函数以图像的形式描述如图3所示。

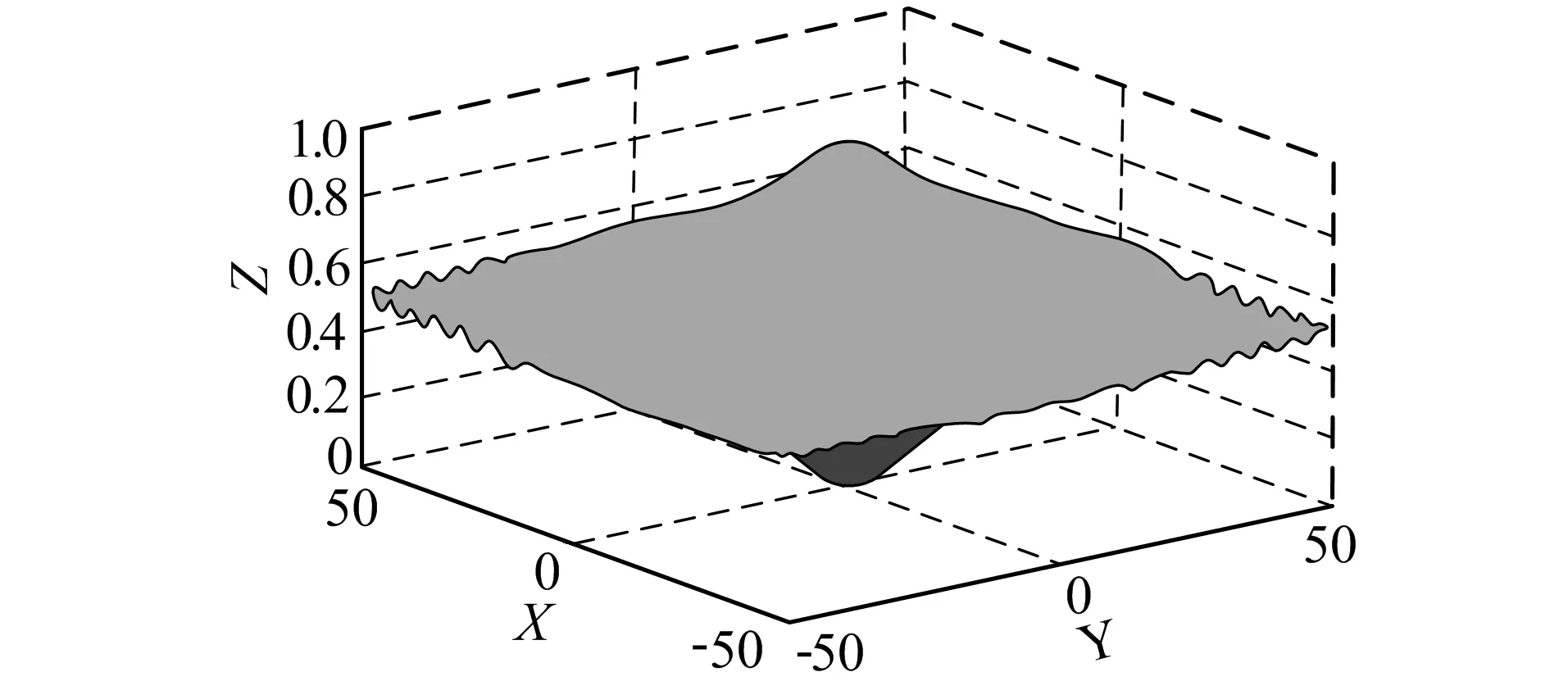
图3 测试函数图像Fig.3 Test function image

将上述测试函数应用于优化算法测试实验中,验证笔者提出优化算法的应用性能。本次实验除了使用笔者所提出的优化算法外,同时采用文献[4]、文献[5]中的算法进行量子优化处理。对比不同算法的优化效果,保证实验结果的合理性。

2.2 实验参数

笔者设计的优化算法应用前,需要计算量子停滞阈值以及与搜索区域半径相关的比例系数。笔者针对上述两个试验参数进行分析,并进行合理设置。

假设量子的初始种群规模为40,将停滞阈值设置为从0开始,不断增长至0.025。针对测试函数进行6次优化,得到图4所示的停滞阈值对测试函数的影响示意图。

由图4可知,停滞阈值的大小直接影响优化算法的应用效果,尤其在停滞阈值范围为0.005～0.015时,函数优化结果最好,这是由于停滞阈值参数设置结果会影响顶层量子聚集程度,[0.005,0.015]的范围既避免了局部极值问题,也保持了算法的局部搜索能力。该实验进行时将停滞阈值选定为该范围内。

图4 停滞阈值对测试函数的影响示意图 图5 比例系数对测试函数的影响示意图Fig.4 Effect of stagnation threshold on test function Fig.5 Effect of scale coefficient on test function

设置量子初始种群规模为40,停滞阈值为0.01,分别将比例系数选定为0.1～0.8,针对测试函数进行8次优化,得到结果如图5所示。

由图5可知,比例系数取值在0.5以下时,测试函数优化效果较差,当比例系数大于0.5,可得到较好的优化结果,并且之后比例系数的增长不会导致测试函数最优解产生较大起伏。因此,该实验将比例系数设置为0.05。

2.3 实验结果分析

实验所采用的测试函数类型为单模态函数,应用笔者所提出的优化算法得到的计算结果如表1所示。

表1 测试函数优化计算结果Tab.1 Test function optimization calculation results

根据表1可知,笔者提出分散性能量子优化算法在不同量子数量、不同维度条件下,均可得出测试函数的最佳优化结果,充分表明所提出优化算法的可行性。通过分析最优解计算结果可知,优化难度随维度的增加而增长,导致算法优化效果较差。

除了笔者提出的优化算法外,应用文献[4]、文献[5]中的优化算法进行多次优化测试,分析不同优化算法的收敛情况,得到结果如图6所示。

图6 3种优化算法的收敛曲线图Fig.6 Convergence curves of three optimization algorithms

由图6可知,3种优化算法的收敛时间分别为t1、t2和t3。其中笔者提出的优化算法收敛时间为10 s,其余两种优化算法的收敛时间为20 s与30 s。综上所述,笔者设计优化算法有效提升了收敛速度,使优化算法收敛时间减少了50%与67%,促进了量子算法的推广应用。

3 结 语

笔者针对具有分散性能的量子优化问题深入分析,提出将非线性混沌网络系统应用于优化过程中,生成新的优化算法。对量子初始化混沌位置进行分析,并分析量子种群停滞性。采用非线性网络系统,建立一种优化控制机制,早熟判定机制完成量子优化算法的设计。依托于混沌网络的随机性、便利性,弥补传统优化算法的不足,将其应用于实际求解过程中,有效减少算法所需的收敛时间。