湿气管道积液的持液率突变行为预测*
沈伟伟 邓道明 李金潮 万宇飞 宫敬
1海军勤务学院
2中国石油大学(北京)油气管道输送安全国家工程实验室/石油工程教育部重点实验室/城市油气输配技术北京市重点实验室
3海洋石油工程股份有限公司
4中海石油(中国)有限公司天津分公司
在我国常规天然气或页岩气资源的勘探与开发逐渐向沙漠和深海等无人区域、地形起伏山区转移的背景下,湿天然气集输工艺因具有经济优势而被广泛采用[1]。川渝地区某高含硫气田和页岩气田都遭遇过积液困扰,积液是湿气管道生产运行中出现的严峻问题之一。湿气管道的液相负荷低,在较高的气相速度下,由于气液相间作用,管道中气体会将大部分液体携带出管道;但当管道输气量减小时,气体对液体的携带能力减弱,导致液体积留在管线内。积液会减小管道有效输送截面积而导致管线压降增大、降低集气能力和影响气井产能,复杂地形条件下会导致清管困难甚至管道腐蚀穿孔[2-3]。
湿气管道积液是天然气集输领域的难点问题,与之对应的倾斜管道积液或气体携液理论研究越来越受到关注,但目前无公认系统的理论模型供工程应用,因为相对于室内的小直径、常压气液管流实验,现场湿气集输管道一般为大直径、高压力。对于长输管道积液,NACE 推荐利用临界角公式计算长输管道不发生积液的临界倾角,以此预测腐蚀风险,但该相关式不适用于湿气集输管道。部分学者借用商用模拟软件(如OLGA、Fluent)建立多相流模型对湿气管道沿线持液率进行计算,在此基础上分析各因素对管线积液的影响,以探求湿气管道积液规律[4-10]。另有学者通过低液相负荷两相流动实验研究湿气管道积液,认为管道中流型由分层流向段塞流转变时会产生积液;通过实验设备记录刚开始积液时的气相表观速度,将其作为临界气速(以下一般简称为临界气速)[11-13]。
临界气速预测最早应用于气井井筒积液问题。与井筒相比,湿气集输管道管径大;当井场或集气站设有分离器时,湿气集输管道的液相负荷一般低于井筒。现有的低液相负荷气液管流或井筒积液研究大多采用小直径低压管道室内实验数据或现场井筒生产数据,将其研究成果放大用于大直径、高压集输管道需要进一步研究。基于气液两相流动理论及最新的低液相负荷管道积液研究成果,本文提出两种高压、大直径湿气管道积液预测方法,计算出的临界气速可为湿气管道的设计和安全运行提供参考。
1 模型建立
由于液相负荷较低,湿气管道内出现的流型多为分层流,而当湿气管道中流型为段塞流时表明管道中已经出现积液。湿气管道积液预测模型中流型包括分层流和段塞流。
1.1 分层流
邓道明等[14]曾尝试建立高压大直径天然气两相管流计算模型,通过将模型计算结果与生产数据比较,认为分层流气液界面为平界面更合理。相较于实验室常见的1 in、2 in 管道,气田开发中遇到的湿气集输管道尺寸一般较大,本文分层流采用平界面模型计算。气液动量方程及各界面剪切应力计算公式见文献[14],公式中气液界面摩阻系数fI采用Andreussi-Persen[15]气液界面摩阻系数形式,气、液相与管壁间的摩阻系数fG、fL分别选用Biberg[16]方程和Nossen[17]方程计算。
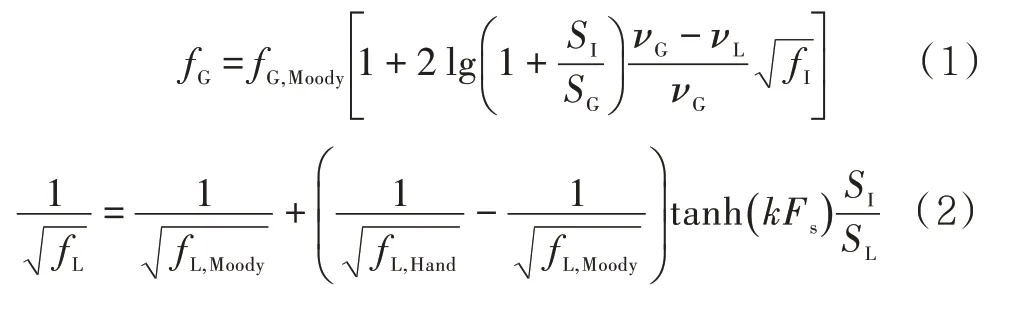
式 中:νG、νL分别为气、液相流速,m/s;fG,Moody、fL,Moody分别为Moody 图计算出的摩阻系数;SG、SL分别为气、液相湿周,m;SI为管道截面上气液分界线的长度,m;k为经验常数,取2 000。
式(2)中Fs计算式如下:

fL,Hand采用SPEDDING 和HAND[18](1997)给出的相关式计算:

式中:τI为气液界面上的剪切应力,N/m;ρG、ρL分别为气、液相密度,kg/m3;D为管内径,m;θ为管道与水平方向的夹角,(°);DhG、DhL分别为气、液相当量水力直径,m;μG、μL分别为气、液相动力黏度,Pa·s;HL为持液率。
1.2 段塞流
对于给定的气、液相表观速度,液塞区液相流速计算公式如下:

式中:νsG、νsL分别为气、液相表观速度,m/s;HGS为液塞区空隙率;HLS为液塞区持液率,计算公式见文献[19];νGS为液塞区气相流速,m/s,计算公式见文献[20]。
液膜区液、气相流速计算公式如下:

式中:νT为液膜区泰勒气泡的运动速度,m/s,计算公式见文献[21];HGF、HLF分别为液膜区空隙率、持液率。
考虑到液膜区和液塞区界面的掺混,液膜区动量方程见文献[19]。与分层流模型相似,通过试算可解出液膜区持液率。液塞区长度由Scott[22]相关式确定,液膜区长度计算公式见文献[23]。
段塞流单元的持液率计算式如下:

1.3 积液判别
湿气管道开始积液时直观表现为气相流速略有减少,管道内持液率显著增大。定义湿气管道内持液率发生突变时对应的气相表观速度为临界气速,相应的状态点为管道不积液向积液转变点(简称积液点)。本文提出两种接近水平上倾湿气管道积液判别方法。
一种方法是基于“最小滑移”流型转变判别法。主流观点认为湿气管道中流型由分层流向段塞流转变时会产生积液,通过模型求解不同工况下流型转变时的气相表观速度,将其作为临界气速。合理的分层流和段塞流转变准则是保证预测结果准确的关键。由于不同流型转变边界的交叉性,基于稳定性的流型转变准则会导致转变边界不连续[21,24]。为避免边界不连续对计算结果产生影响,本模型中分层流与段塞流转变采用“最小滑移”准则。“最小滑移”准则指的是选择气、液相速度差最小(从而持液率最低)的流型作为管道中的流型,用于高压两相管流计算结果较为准确[23]。OLGA 软件的流型判别采用了该准则[21,25],只是其具体的公式和算法没有公开。
另一种方法是湿气管道分层流持液率多解法。在某些工况下,低液相负荷湿气管道分层流的持液率具有多解,认为此时可通过分层流动量方程持液率多解工况区来预测湿气管道临界气速——多解工况区的最小气相表观速度为临界气速。
2 模型验证
模型验证包括实验数据验证及软件对比验证。
2.1 实验数据验证
公开的较大直径(不小于3 in)、低液相负荷下接近水平管道积液实验数据较少。FAN(2015)[12]利用图尔萨大学3 in 管道进行了低液相负荷下常压气液两相流动的积液特性实验:实验介质为空气和水,实验管道倾角介于2°~20°之间,液相表观速度为0.005 m/s,气相表观速度为2~32 m/s。实验过程管道内出现的流型包括分层流和段塞流,FAN 将实验观察到的维持分层流的最小气速作为临界气速。不同倾角下临界气速观测值及本文模型预测的临界气速如表1 所示。

表1 Fan 实验临界气速观测值及本文模型预测值Tab.1 Critical gas velocities observed by Fan experiment and predicted by the model
从表1 中数据可以看出:基于“最小滑移”流型转变判别法(方法1)和湿气管道分层流持液率多解法(方法2)预测临界气速结果几乎一致;随着管道倾角增大,实验观测临界气速也增大,本文模型预测与实验结果呈现相同的趋势;模型预测的临界气速与实验值的相对误差不超过±8%,模型预测结果较为准确。
LANGSHOLT[11]在IFE 的4 in 管道中进行了气液低液相负荷流动实验,实验介质包括水、溶剂油(ExxsolD80)和六氟化硫(SF6)气体,实验压力为0.35 MPa 和0.71 MPa,液相表观流速设置为0.001 m/s,实验数据可用于模型的验证。不同实验条件下管道中持液率突增时对应的气体流速及本文模型预测的临界气速如表2 所示。
从表2 中数据可以看出,基于“最小滑移”准则流型转变判别法和湿气管道分层流持液率多解法预测临界气体流速结果整体较为接近。与实验结果比较,湿气管道分层流持液率多解法预测结果相对更准确,但随着管道倾角增大,两种方法预测结果趋于一致;实验观测临界气速随管道倾角的增大而增大,随压力的增大而减小,本文模型预测结果与实验呈现相同的趋势;模型预测的临界气速与实验值的相对误差均不超过±11%,且绝大多在±10%以内。

表2 Langsholt 实验临界气速观测值及本文模型预测值Tab.2 Critical gas velocities observed by Langsholt experiment and predicted by the model
2.2 软件对比验证
因室内实验压力大多为常压或接近常压,实验管道尺寸相对较小,而高压、大尺寸管道实验数据暂未公开,可用的适于研究湿气集输管道积液预测的低液相负荷两相流动实验较少。为补充高压、大尺寸管道实验数据缺失的局限,并对模型可靠性作进一步验证,在此增加本文模型预测结果与OLGA软件(一般认为OLGA 软件来自高压大直径管道实验)的对比验证。
模拟管道中介质为天然气和水,天然气组分见表3。管道基准数据为:运行压力为5.0 MPa,管道倾角为2°,管径为12 in,液相表观速度为0.001 m/s。利用所建模型计算分析管道倾角、管径、液相表观速度、压力对临界气速的影响;同时使用OLGA 软件多次模拟不同气相表观速度工况,间接计算出临界气速,并与本文模型计算结果对比。

表3 天然气组成Tab.3 Natural gas composition 摩尔分数/%
在基准数据下,采用“最小滑移”流型转变判别法计算出来的临界气速为3.7 m/s。为更直观地展现模型计算情况,在图1 中作出该方法计算出来的持液率随气相流速变化的关系(蓝线);图1 中红色的点是模型计算出的分层流持液率的解,多解区域的左边界对应的气相表观速度也为3.7 m/s;采用OLGA 模拟不同气相流速下的持液率,如图1 中绿点所示。根据前文定义持液率突变对应积液,间接得出临界气速为3.3 m/s,与模型计算结果较为接近。
从图1 中可以看出:本文模型预测的湿气管道分层流、段塞流持液率和OLGA 计算接近。基于“最小滑移”流型转变判别法预测的临界气速两侧持液率变化不连续,当气速低于临界气速时,管道中流型由分层流转变为段塞流,持液率突增,管道中开始积液;观察分层流持液率解的曲线可以发现,在一定的气速范围内,持液率方程存在多解,且多解区域左侧对应的气速与基于“最小滑移”流型转变判别法计算出的临界气速相同。两种方法预测的临界气速两侧持液率均发生突变,与前文积液点的定义相符。
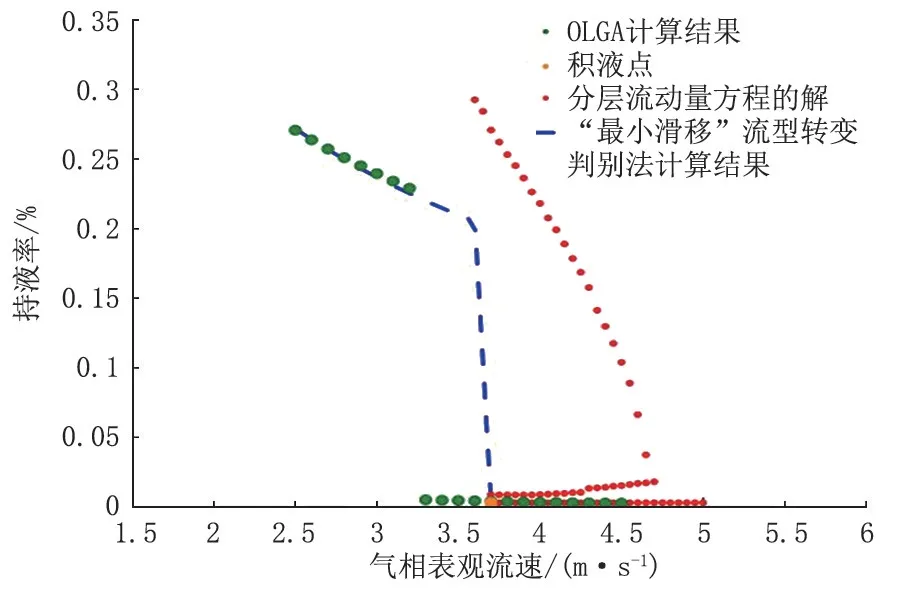
图1 基准参数下模型及OLGA 预测结果Fig.1 Model and OLGA prediction results under reference parameters
2.2.1 管道倾角
基准参数中改变管道倾角,不同倾角下模型预测趋势与图1 类似。倾角为1°、2°、3°、5°时基于“最小滑移”流型转变判别法或分层流持液率多解法预测的临界气速分别为3.1、3.7、4.2、和5.0 m/s;OLGA 间接预测出的对应临界气速分别为2.7、3.3、3.8、4.5 m/s。本模型预测的临界气速与OLGA 预测结果较为接近,且高于OLGA 预测值。随着倾角的增大,模型预测的临界气速不断增大,这与OLGA 预测趋势相同。分析原因,随着管道倾角的增大,液体所受重力沿管道方向的分力增大,气体将液体携带出管道所需要的界面剪切应力也增大,而气液界面剪切应力与气液相流速差有关,在液相流速接近不变的情况下,对应的临界气速将会增大。
2.2.2 管径
基准参数中改变管道直径,基于“最小滑移”流型转变判别法或湿气管道分层流持液率多解法,预测的管径为12、16、20、24 in 时临界气速分别为3.7、4.3、4.8 和5.3 m/s;OLGA 间接预测出的对应临界气速分别为3.3、3.8、4.2、4.5 m/s。模型预测的临界气速与OLGA 预测结果较为接近,且随着管径的增大,模型预测的临界气速不断增大,这与OLGA 预测趋势相同。计算过程跟踪显示,管径越大,气液界面摩阻系数越小,即气体携液能力越小,相应的临界气速越大。
2.2.3 压力
基准参数中改变管道操作压力,管道操作压力为3、5、7、9 MPa 时基于“最小滑移”流型转变判别法或湿气管道分层流持液率多解法预测的临界气速分别为4.9、3.7、3.1 和2.7 m/s;OLGA 间接计算出的对应临界气速分别为4.3、3.3、2.8 和2.4 m/s。模型预测的临界气速与OLGA 预测结果较为接近,且随着压力的增大,模型预测的临界气速不断减小,这与OLGA 预测趋势相同。分析原因,管道中压力增大会使得气相密度增大,由气液相界面剪切应力表达式可知,气体对液体的携带能力增强,相同情况下需要较小的气速就能将液体携带出管道,因此临界气速将会减小。
2.2.4 液相表观速度
对应于不同液相负荷,改变基准参数中的液相表观速度,OLGA 及本文模型预测的不同液相负荷下临界气速如表4 所示。值得注意的是,对于液相表观速度为0.003、0.004 m/s 时,基于“最小滑移”流型转变判别法与湿气管道分层流持液率多解法计算出的临界气速不再相同。例如,液相表观速度为0.003 m/s 时,基于“最小滑移”流型转变方法计算出的临界气速为4.2 m/s。程序追踪表明,管道中气相流速为4.3 m/s 时持液率已经开始突变,也就是说流型转变与湿气管道积液不完全对应,OLGA 模拟过程中也有类似的结论。即随着气相流速的减小,在流型转变前已经发生了持液率突变(即积液)。而分层流持液率多解法计算结果仍与积液对应。

表4 不同液相表观速度下OLGA 及本文模型预测临界气速Tab.4 Critical gas velocities predicted by OLGA and the model under different liquid apparent velocities
表4 中本文两种方法预测的临界气速与OLGA预测结果仍较为接近,且随着液相表观速度的增大,模型预测的临界气速不断增大。分析原因,气液界面剪切应力与气液相流速差有关,在液相流速增大(液量增多)的情况下,需要更大的气速才能将管道中液体携带出,因此临界气速将会增大。
3 结论
基于气液两相流动理论及最新的低液相负荷管道积液研究成果,改进并优选了封闭关系式,建立了湿气管道积液预测模型,提出了两种接近水平湿气管道积液判别方法——基于“最小滑移”的流型转变判别法和湿气管道分层流持液率多解法,依照模型编程后可直接计算出不同工况下湿气管道临界气速。通过现有实验数据和OLGA 软件验证,本文模型预测的湿气管道分层流、段塞流持液率以及临界气速较为可靠。利用本模型计算分析了管道倾角、管径、运行压力及液相表观速度对临界气速的影响,得出以下结论:
(1)湿气管道的流型转变对应或近似对应于积液的发生,采用“最小滑移”流型转变判别法计算积液临界气速具有一定普适性。而在某些工况下,湿气管道分层流存在持液率多解,持液率多解区域左边界对应的气相表观速度即为积液的临界气速,此时采用湿气管道分层流持液率多解法预测积液临界气速更为方便。
(2)对于高压、大尺寸湿气管道,文中所列参数下模型计算的临界气速介于2.7~5.3 m/s,与规范NB/T 14006—2015、SY/T 0612—2014 推荐的经验值3~5 m/s 接近。
(3)随着管道倾角、管径、液相表观速度的增大,临界气速增大;随着运行压力的增大,临界气速减小。模型计算的各因素对临界气速的影响与OLGA 软件预测结果一致。

