“概率论与数理统计”课程教学改革探索与实践
张水利 屈聪
平顶山学院数学与统计学院 河南平顶山 467000
“概率论与数理统计”是高等院校理工类、经管类专业学生的必修课程,是研究随机现象数量规律的一门学科,它应用非常广泛,几乎遍及自然科学和社会科学的各领域。对该课程的学习,有助于培养学生随机事件应对能力、数据处理与建模能力、解决和处理社会生活中随机问题的意识和能力。随着教育技术的发展,以知识灌输为主的传统教学模式已经不能适应新时代的大学教育要求,以学生为中心的教学模式渐渐涌出,如何构建以学生为中心的新式课堂,这就需要所有的任课教师调整教学方式,整合教学内容,改善教学理念,改进教学模式。在教学中贯彻以学生为中心、成果为导向、持续改进的教学理念,积极进行教学模式和教学方法改革,适应高等教育的要求,切实提高教学质量,是该课程进行教学改革的目标和方向。
1 “概率论与数理统计”课程教学现状
“概率论与数理统计”是一门以研究随机现象统计规律为对象的数学学科,属于随机数学范畴,具有较强的理论性和实践性,是抽样调查、产品检验、统计预测、统计决策等方面的理论支柱。在“概率论与数理统计”课程的教学中主要存在以下问题:
(1)重理论轻实践。对“概率论与数理统计”的基本概念、定理、习题等理论部分讲授比较详细,而与日常生活、学生所学专业结合的实际案例讲得比较少,对利用数学或统计软件解决实际问题的实验重视不够,导致学生自己动手解决实际问题的能力比较欠缺,不利于应用型人才目标的实现。
(2)教学模式落后。传统的教学模式中教师占主导地位,课堂的教学质量依赖于教师的教学水平,不能体现学生在教学中的主体地位。教学是“填鸭式”和“灌输式”的模式,学生是被动学习,不能很好调动学生学习的积极性和主动性。
(3)考核方式单一。在考核方式方面,很多高校以期末考试成绩为主,平时成绩以考勤和作业进行评定,占比较小。这种考核方式会使部分学生平时学习不认真,在期末考试前通过复习、背概念公式来应对考试,对课程体系缺乏系统的认知。同时这种考核方式只考核了学生知识掌握情况,缺少能力的考核和评价。
针对教学过程中存在的问题,许多教师积极探索在“概率论与数理统计”教学中进行改革和尝试,并取得了一定的效果。例如,段宝彬、丁芳清、牛欣通过贴近实际或学生所学专业相关的精彩案例和设计不同类型的自主学习项目,增强学生的应用意识和实践动手能力;习丽通过调整教学内容,采用线上线下混合教学模式,提高教学效果,提升学生的自主学习能力;沈爱婷、张玉在教学过程中贯彻“以人为本”的教育理念,从学生的角度和实际情况出发,进行教学设计和开展教学;徐尔等进行了翻转课堂和线上线下混合式教学,实施全程性和多元化的考核方式,从“知识传授型”到“能力培养型”转变;闫莉等从教学主体、教学理念与目标、教学内容与资源、教学过程、教学手段与方法、教学评价等方面分析了课程思政教学设计的逻辑框架;刘淑环以教学案例引入大量的生活常识、谚语、搭建知识结构体系等教学方式,引导学生把“概率论与数理统计”知识应用于实际生活,将辩证唯物主义、社会主义核心价值观等思政元素融入课程教学中,实现立德树人的目标;张艳伟主要从思政教育融入“概率论与数理统计”教学中的方法、实施步骤两个方面来阐述如何在“概率论与数理统计”教学中进行课程思政,在实施步骤方面,从概率统计概念、概率统计定理、概率统计原理、概率统计方法等四个方面来阐述实施课程思政的过程;吴波以“概率论与数理统计”为案例,对金课的特征进行了分析,从教学的难度、教学的深度、教学的广度、教学的高度、教学的强度、教学的精度和教学的温度等七个方面进行了阐述和分析,在分析过程中列举了大量的案例,具有一定的示范性和推广性;储亚伟、叶薇薇、王海坤以“一阶非齐次线性微分方程的解法”为例,探讨了基于BOPPPS教学模式的高等数学微课程教学设计的方法,在教学设计中,将数学思想方法融入课堂教学,以学生为中心、以问题为导向的探究式教学,注重知识的认知过程,强调从已知到未知的自然过渡的互动式教学。
2 以问题为导向,推进课堂教学改革与创新
为了提高课堂教学效果,达到人才培养目标的要求,针对传统课程教学中存在的问题,需要进行教学模式、教学方法、教学评价等方面进行创新。
2.1 推进BOPPPS教学模式,提升学生课堂参与度
BOPPPS教学模式是加拿大教师技能培训中广泛使用的教学模式,是一个能够协助教师拆解并分析教学过程、发现教学盲点、提升教学成效的有效工具。在该教学模式中,共分为六个环节:导入(Bridge-in)、教学目标(Objective/Outcome)、前测(Pre-assessment)、参与式互助教学(Participatory learning)、后测(Post-assessment)和总结(Summary)。在导入环节,以生活中的实际案例引入新知识,增加课程的吸引力和数学应用能力的培养,也可以通过已经学过的知识导入新内容;在前测环节,测试学生本节课使用且已学过的知识,了解学生的知识掌握情况,根据学生掌握知识的情况,调整教学内容和教学方法,做到有的放矢;在参与环节,以学生分组讨论为主,教师进行点评,提高学生的参与度,体现学生为主体的教学理念;在后测环节,对本节课知识进行测试,了解学生本节课知识的掌握情况,发现问题,教师能够及时改进教学进度和调整教学方法;在总结环节,以言简意赅的形式,总结重点内容,便于学生掌握。
2.2 实施课程思政,提升学生学习积极性和课程认同感
概率论与数理统计与实际社会联系非常紧密,有非常丰富的思政案例,可以从“概率论与数理统计”课程中的概念、定理、原理等方面挖掘课程思政元素,并在教学中融入思政教育。例如概率与频率的概念、中心极限定理、小概率事件原理等。
概率和频率反映了本质和现象的对立统一的唯物辩证法思想。概率具有稳定性和必然性,它反映的是随机现象的本质;频率具有随机性和波动性,它是变化的,但是由伯努利大数定律可知,随着试验次数的增加,频率稳定于概率,具有稳定性的特征,它是对概率的一种直观体现。
设事件发生的概率为>0(的值比较小),在次独立重复的试验中至少发生1次的概率为:
1-(1-)→1,→∞
即使一个事件发生的概率很小,在很多次试验中一定会发生。这个公式也能够解释“水滴石穿”等谚语。
通过与实际社会生活联系紧密的课程思政案例,缩短数学与学生之间的距离感,提高学生学习的兴趣和积极性,提高学生的社会责任感和课程的认同感。
2.3 实施过程化评价,提升学生实践能力和学习的持续性
为了解决考核单一问题与BOPPPS教学模式相适应,本课程采用过程化评价方式,不仅考核知识的掌握情况,而且考核课程思政的效果和利用软件解决实际问题的能力,具体包括考勤、预习作业、课后作业、单元测试、期中测试、课程论文、课程总结与反思、期末考试等环节,通过动态的评价和分析,不断调整课程教学方法,在课程结束时基本完成课程的培养目标。
3 贯彻学生中心理念,促进学生全面发展
在教学过程中,不断贯彻和深化以学生为中心、成果为导向、持续改进的教学理念,从创新教学设计、创新教学手段等方面着手,促进学生全面发展。
3.1 打造线上教学资源,丰富学生学习途径
以学习通为平台,建设丰富的教学资源,每一章节包括PPT、课程视频、习题、单元测试、案例库等教学资源,方便学生课下自学,为学生提供处处能学、时时可学的教学资源。
3.2 创新课堂教学设计,提高学生学习效率
在以学生为中心的理念下,结合课程思政的目标,利用BOPPPS教学模式进行教学设计,做到突出重点,化解难点,提高学生学习的效率,力争做到知识传授、能力培养和价值引领有机融合,落实立德树人的根本任务。
下面以随机变量的数字特征——离散型随机变量数学期望的教学设计为例,说明如何创新课堂教学设计,如下表所示。
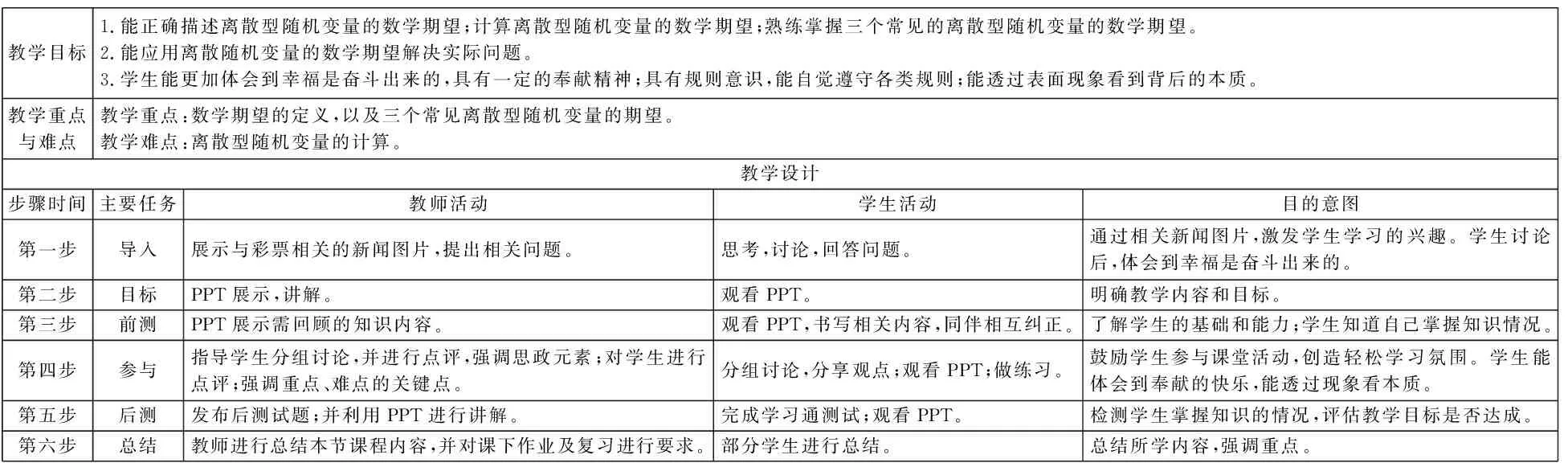
离散型随机变量数学期望的教学设计表
3.3 创新课堂教学手段,激发学生学习兴趣
采用多媒体教学(视频、图片),利用互联网技术、信息技术为课程改革提供技术支撑,设计合理的教学环节,利用超星学习通课程平台,在课堂上进行签到、知识抢答、随机选人、随堂练习、分组讨论、章节测试、习题推送、问题解答等活动。
3.4 落实“金课”建设,全面提高人才培养质量
本课程立足以学生为中心的教学理念,聚焦“两性一度”,促进学生的全面发展。在课程教学中,注意课程高阶性、创新性和挑战度,在课程论文中,让学生利用统计软件SPSS或R语言分析和处理实际问题,得出结论并进行分析,提高课程的创新性;在教学过程中,把“概率论与数理统计”一些最新成果引入课堂,提高课程的高阶性;增加一些设计性课题或项目,利用参数估计,设计一种方案,如何估计某水库中鱼数量,提高课程的挑战度。
结语
本课程使用的BOPPPS教学模式进行教学设计,有导入、前测、参与、后测等环节,既可弥补学生基础知识掌握不牢的不足,也可以提高学生的课程参与程度,解决传统课堂中以教师教学为主的问题。同时,BOPPPS教学模式是一种比较普适的教学模式,基本上适用于所有课程,能够较容易推广到其他课程中。
课程思政是在专业课程中融入思政元素,在传授知识、培养能力的同时,也注重价值塑造和价值引领。在专业课程中,均有课程思政元素,课程思政可以解决学生思想问题,挖掘学生内在动力,进而提高人才培养质量。
因此,“概率论与数理统计”课程在教学改革方面的经验可以较好推广到其他课程中去,为课程教学改革与探索提供一定的参考和借鉴。

