上软下硬复合地层中盾构隧道开挖面稳定性分析

肖红菊，孙玉永

（1.铜陵学院 建筑工程学院，安徽 铜陵 244000；2.铜陵学院 建筑信息技术研究所，安徽 铜陵 244000）

随着我国城市轨道交通工程的大量兴建，区间盾构隧道穿越的地层也越来越复杂，如穿越深厚软黏土层［1-2］、上软下硬复合地层［3-5］、富水地层［6-7］等。对于上软下硬复合地层，盾构刀盘切削下部岩层效率低，会造成盾构刀盘反复切削上部软弱地层，从而造成上部软弱地层超挖甚至坍塌失稳等情况，进而对周围环境产生不利影响，如土家湾隧道［8］。

国内外学者针对盾构隧道开挖面稳定分析和控制进行了大量研究工作，并取得了诸多卓有成效的研究成果。在隧道开挖面失稳模式方面，Chambon等［9］通过进行均质砂土层隧道开挖面稳定的离心模型试验，发现隧道开挖面破坏区域为筒仓状，破坏形态为楔形体。Kamata等［10］也通过离心试验得到了相似的结论。Mair 等［11-12］在前人研究的基础上发现，砂土层中开挖面破坏形状为烟囱状，黏土层中为漏斗状。付亚雄等［2］通过进行软黏土地层中盾构隧道开挖面稳定性离心模型试验发现，开挖面两侧滑动破裂带呈漏斗状。安永林等［5］通过分析上软下硬地层对隧道稳定性的影响发现，开挖面软弱地层相对厚度系数越大，稳定性越差。雷华阳等［13］借助于透明黏土开展了盾构隧道开挖面失稳室内试验，发现开挖面失稳可分为3个阶段，具有明显的分区特征，且失稳区呈椭圆状。在隧道开挖面失稳分析模型方面，Horn［14］最早提出了三维楔形体模型，之后众多学者对楔形体模型进行了修正；魏纲等［15］提出了砂性土层中隧道开挖面支护压力计算的梯形楔形体模型；闫军涛等［4］也将该模型应用到上软下硬土层中，并收到了较好效果。在分析方法方面， 目前主要有模型试验法［2-3，10-11］、数值模拟法［1，5，14］及解析法［4，15］等。

徐州市轨道交通2 号线1 期工程周庄站—七里沟站区间（简称“周七区间”）采用盾构法施工，左线隧道全长1 168.823 m，右线隧道全长1 160.541 m，区间最大坡度26‰，最小坡度5‰，隧道顶部埋深10.00~17.00 m。周七区间从上至下的土层主要为①1杂填土层、②5-3黏质粉土、②3-2层黏土、②3-3层黏土、⑤3-4层黏土、⑪2-3层中风化灰岩及⑪2NH-3层中风化泥灰岩，隧道穿越地层主要为⑤3-4层黏土、⑪2-3层中风化灰岩以及⑪2NH-3层中风化泥灰岩，其中⑤3-4层黏土层为徐州地区的老黏土，呈硬塑状态，中等压缩性，强度较好，工程性质较好；⑪2-3层中风化灰岩为较硬岩，风化程度较弱，但节理或裂隙、溶蚀、岩溶发育，发育规律性差且富水，为典型的上软下硬复合地层，区间地质纵断面图如图1所示。

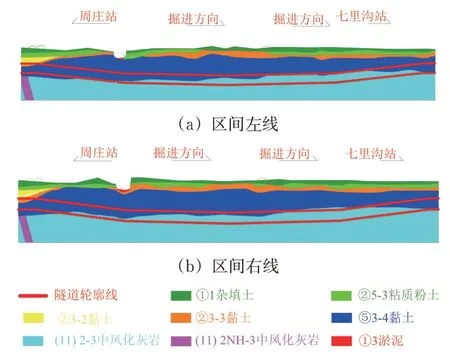
图1 周七区间地质纵断面图

本文以徐州市轨道交通2 号线周七区间隧道工程为背景，在前人研究成果的基础上，主要对盾构隧道在上软下硬复合地层中掘进施工遇到的开挖面稳定性问题进行系统分析，解决工程中的技术难题，同时也可为类似工程提供借鉴。

1 复合地层中盾构隧道开挖面变形特性和破坏模式

盾构在上软下硬地层中掘进时，由于下部硬土层的强度和刚度较大，盾构掘进速度较慢，这会对上部软弱地层造成过度切削，进而诱发上部地层坍塌，即上软下硬地层中盾构隧道开挖面的变形特性和破坏模式与均质地层可能存在差异。因此，以徐州市轨道交通2 号线一期工程周七区间隧道工程为背景，借助数值模拟的方法对上软下硬地层中盾构隧道开挖面变形特性和破坏模式进行研究。

借助PLAXIS 3D 有限差分软件，建立三维分析模型如图2 所示。图中：y 轴方向为盾构掘进方向，长50 m；x 轴方向与掘进方向垂直，宽50 m；z 轴方向为深度方向，高40 m；沿深度方向包括3层土体，即②3-2层黏土（蓝色）、⑤3-4层黏土（绿色）和⑪2-3层中风化灰岩（黄色）。土体的物理力学指标见表1。盾构隧道外径6.2 m、内径5.5 m，管片厚度0.35 m，隧道埋深17.00 m。为了构建上软下硬地层，计算中假定⑤3-4层黏土层的层底埋深19.5 m，也即隧道上部2.5 m在软土层中，下部3.7 m 在中风化灰岩中。计算中土体采用Mohr-Coulomb本构模型，管片采用线弹性本构模型，模型底部采用3 向约束，x 和y 方向采用轴向约束，土体顶部为自由表面。

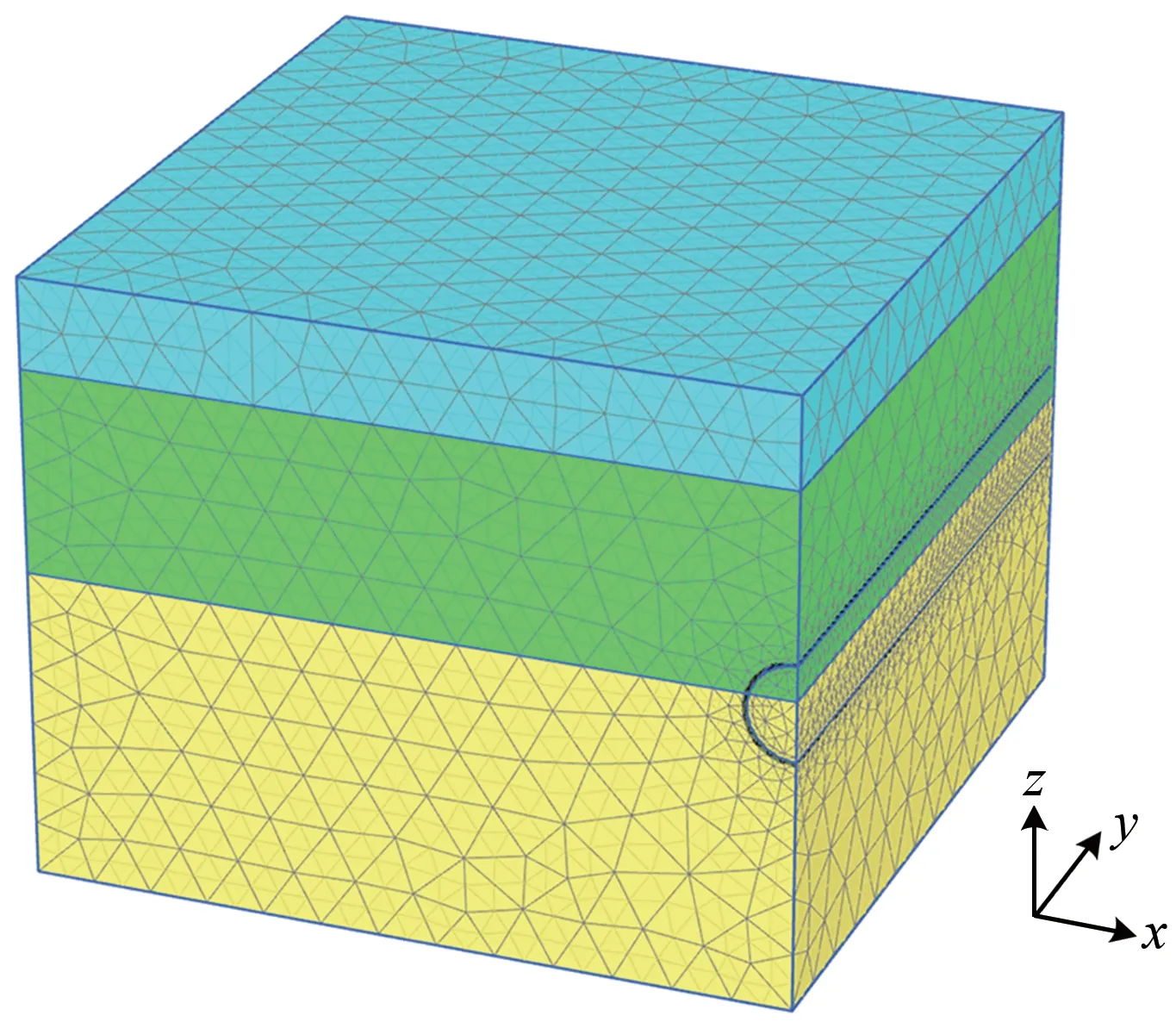
图2 三维有限差分模型

表1 土体的物理力学指标

由既有研究成果［4］可知，土体强度对隧道开挖面变形特性和破坏模式影响不大，故重点研究土层弹性模量对其的影响。为此引入弹性模量比，即上部软土层与下部硬岩的弹性模量之比，计算中保持上部土层参数不变，下部土层取弹性模量比分别为100，20，10，5，2.5 和1.25。弹性模量比为100，10，5 及1.25 条件下土体整体变形云图如图3所示。

由图3 可知：上软下硬地层弹性模量差异越大，上下地层的差异变形就越大（上部变形明显大于下部），在盾构掘进过程中就越易造成上方土层的过大变形甚至失稳；随着上软下硬地层弹性模量比的减小，上下地层的差异变形逐渐缩小；当上软下硬地层弹性模量比接近1（图3（d）为1.25）时，开挖面最大变形发生在隧道中心，且整个开挖面地层变形差异性很小。

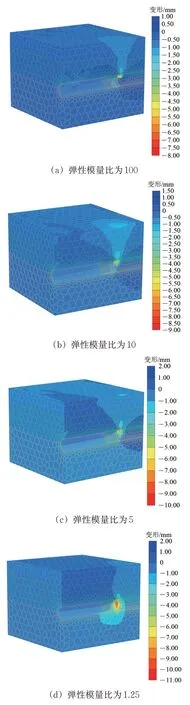
图3 不同弹性模量比下土体变形云图

为了定量分析上下土层弹性模量比对隧道开挖面内中轴线上y 方向位移的影响，不同弹性模量比下隧道开挖面中轴线上y方向位移对比如图4所示。图中：红色圆圈为隧道；红色横线为上软下硬地层的分界线。

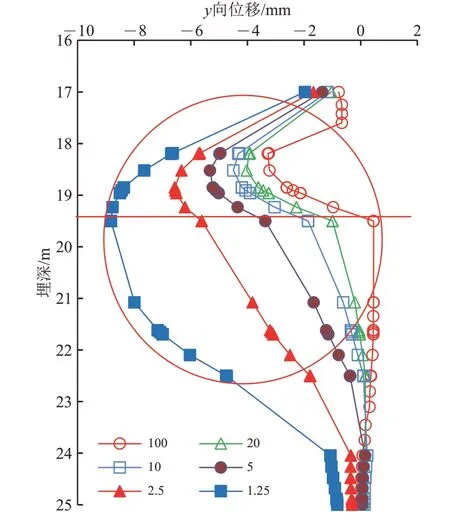
图4 隧道范围内中轴线y方向位移曲线

由图4 可知：随着上软下硬地层弹性模量比的增大，上下地层的y 方向最大位移差值越来越大，如弹性模量比为1.25时，上下地层的y方向最大位移分别为－8.76 和－8.82 mm，两者比值为0.99；弹性模量比为5 时，上下地层的y 方向最大位移分别为－5.32 和－3.37 mm，两者比值为1.58；弹性模量比为10时，上下地层的y方向最大位移分别为－4.49 和－1.86 mm，两者比值为2.41；弹性模量比为100 时，上下地层的y 方向最大位移分别为－3.28 和0.45 mm，两者比值大于8；上软下硬复合地层中，盾构掘进施工引起开挖面变形主要集中在上部软弱地层，且随着上软下硬地层弹性模量比值的增大，该差异逐渐加剧。

为了获得上软下硬地层不同弹性模量比下盾构隧道开挖面的破坏模式，弹性模量比分别为5，10和100 时开挖面沿y 方向的变形云图如图5 所示。由图5可知：当上软下硬地层弹性模量比较大（本文计算值为10）时，开挖面的变形主要集中在上部软土层，而下部硬岩中的变形很小，即开挖面的破坏主要发生在上部软弱地层中；当上软下硬地层弹性模量比较小时，下部硬岩的变形已与上部软弱地层的变形相连通，即开挖面将发生整体破坏。

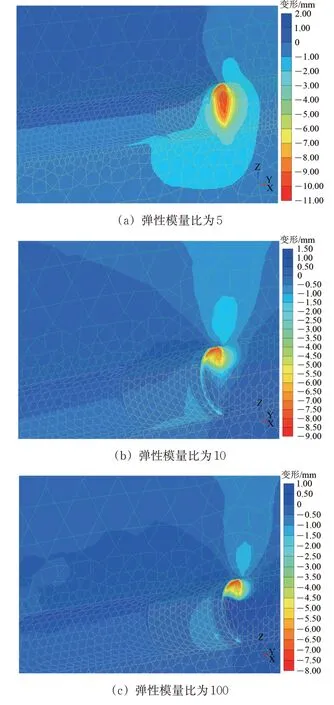
图5 不同弹性模量比下开挖面变形云图

2 上软下硬地层的稳定性判定

2.1 判定方法

盾构隧道在掘进过程中，由于土体受到施工扰动且损失了部分土体，开挖面前方土体会形成1个三维松动区，大量研究者通过理论研究和模型试验发现盾构隧道开挖面破坏模式为楔形体［14］。之后不断有学者对楔形体模型进行改进，使得楔形体模型的计算结果越来越接近工程实测和离心模型试验结果，其中比较准确的为梯形楔形体模型［4，15］。

当隧道开挖面前方为单一土层时，开挖面前方土体破坏形式为整体破坏；当开挖面前方为上软下硬复合地层时，开挖面前方土体破坏形式通常为上部软弱土体的局部破坏。为此，本文在既有研究成果基础上，提出上软下硬地层盾构隧道开挖面的部分梯形楔形体破坏模型，如图6 所示。图中：B 为等效正方形破裂面的边长；D 为隧道直径；α 为梯形楔形体倾角；l 为滑动楔形体的高度（即软硬地层分界面到隧道顶部的距离）；β 为梯形截面底角；z1，z2…为成层土的厚度。

图6 部分梯形楔形体模型

部分梯形楔形体模型由梯形棱柱体和梯形滑动块组成，如图7 所示。梯形楔形体受力情况如图8所示。图中：G 为滑块体的自重；σv为上覆土压力；N为滑动面法向作用力；T为滑动面摩阻力；p为开挖面支护压力。根据滑动块的受力平衡，可以推导上软下硬地层中盾构隧道开挖面稳定判定式。

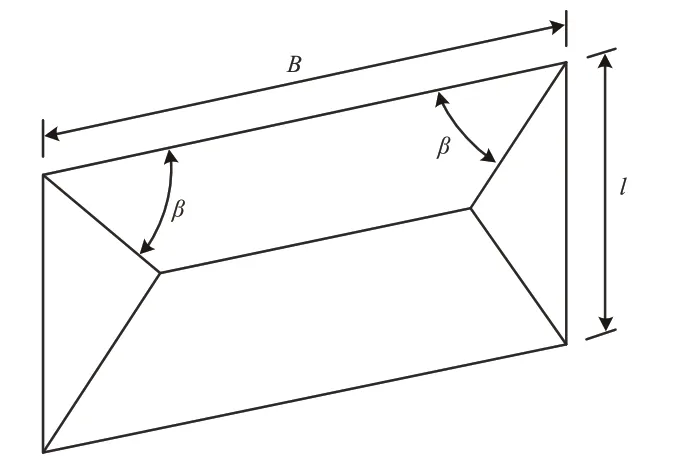
图7 梯形楔形体形状

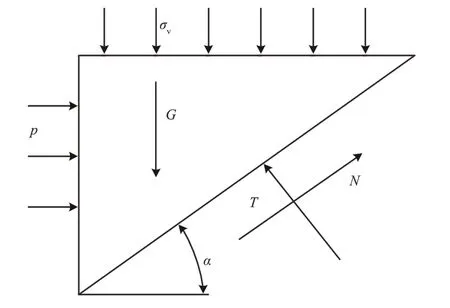
图8 梯形楔形体受力

假定图6 中正方形面积与隧道开挖面面积相等，则有

索科洛夫认为，在土体中存在卸荷拱的条件下，滑动体与卸荷拱接触面上无应力。因此，梯形楔形体块上受到的作用力包括以下几个方面的分力。

1）自重G

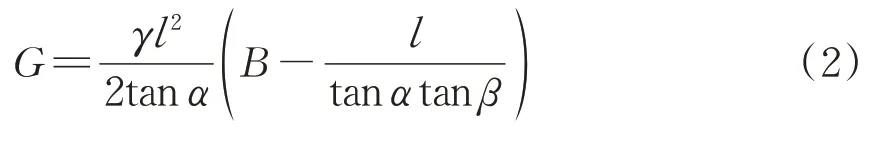
其中，

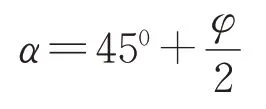
2）上覆土竖向压力pv

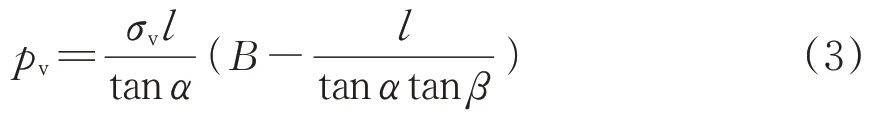
3）滑动面摩阻力T

根据Mohr-Coulomb强度准则可知

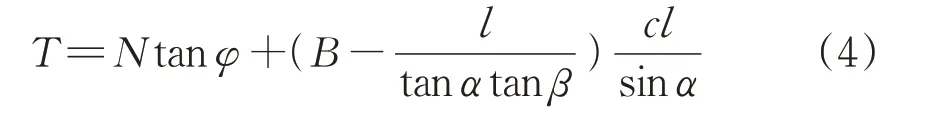
4）开挖面支护压力p

当梯形滑块体处于极限平衡状态时，由水平向受力平衡可知

由竖向受力平衡可知

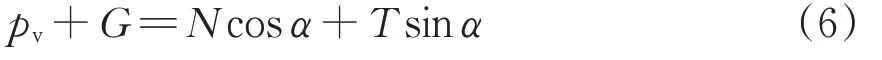
联立式（4）－式（6），可求得支护压力为

其中，

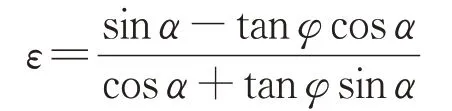
式中：ε 为与梯形楔形体倾角和土体内摩擦角相关的系数；β根据试验结果可取50o。

2.2 上覆土压力

隧道上覆土压力σv是1 个关键参数，其计算方法主要有全覆土重理论、普式土压力理论、太沙基松动土压力理论等［4］，当上覆土体的厚度远大于隧道的外径时，太沙基松动土压力理论更实用，因此采用太沙基松动土压力理论进行计算。

1）均质土层

太沙基松动土压力是在假定平面应变条件下通过二维结构受力分析得到的。在隧道掘进施工过程中，实际开挖面滑动区上方土体是1个三维体，假定松动区为梯形棱柱，把太沙基松动土压力扩展到三维空间，如图9 所示。图中：p0为地面荷载；z为计算点的上覆土厚度。

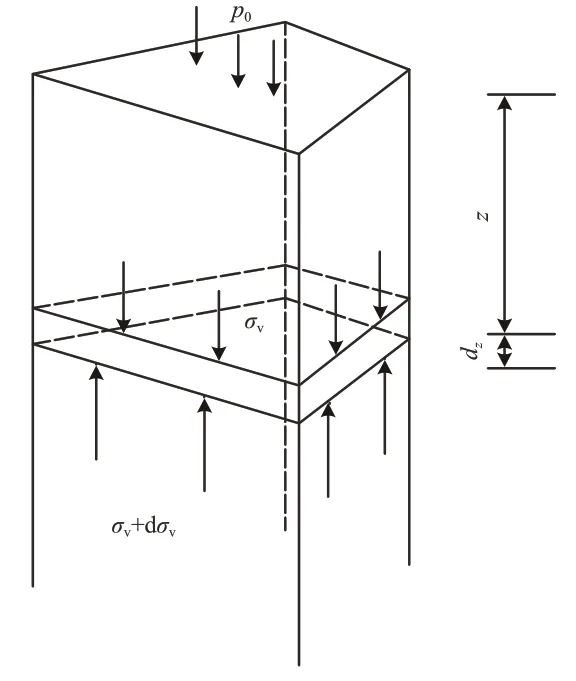
图9 松动土体单元受力示意图

建立松动土柱单元竖向受力平衡方程为

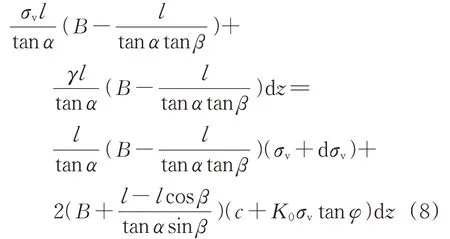
式中：K0为土体的静止侧压力系数。

求解可得上覆土压力值计算式为

其中，

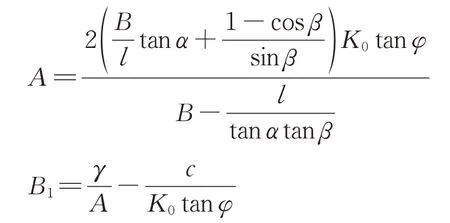
式中：C为待定系数。

由边界条件：z=0，σv=p0，可得任意深度z处的三维上覆土压力计算式为

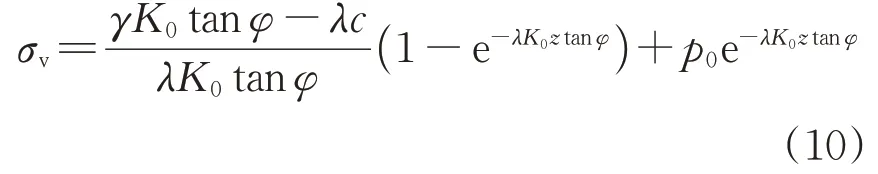
其中，

式中：λ 为与l 有关的参数，只能通过试算来获得l的具体数值。

令z=H（隧道顶的覆土厚度），即得到隧道顶部的上覆土压力值。

2）成层土

太沙基松动土压力理论假定土层条件为均匀地质条件，而在实际工程中，上覆土层往往为成层土，因此有必要把太沙基松动土压力理论扩展到上覆土层为成层土的情况。成层土太沙基松动土压力计算示意图如图10 所示，图中zi，γi，ci和φi分别为土层i（i=1，2，…，n）的厚度、重度、黏聚力和内摩擦角。假定土层i 与土层i+1 之间的相互竖向作用力为Pi，把上部土层作用力假定为超载，可得到Pi为

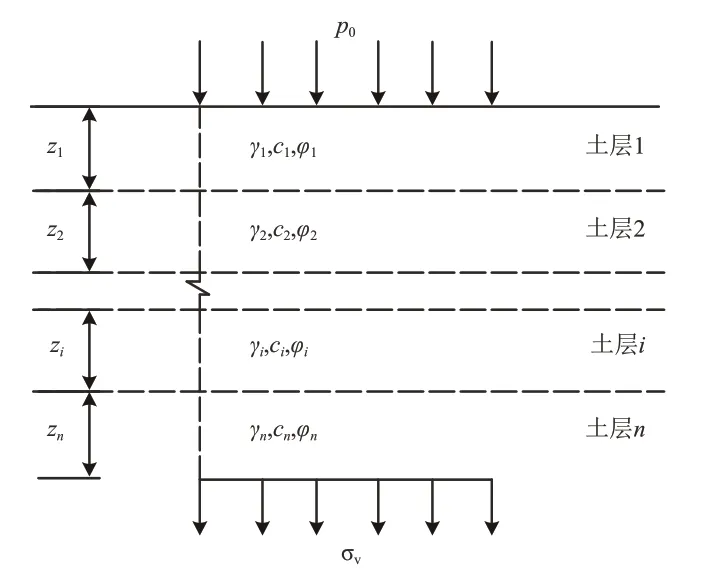
图10 成层土太沙基松动土压力计算示意图

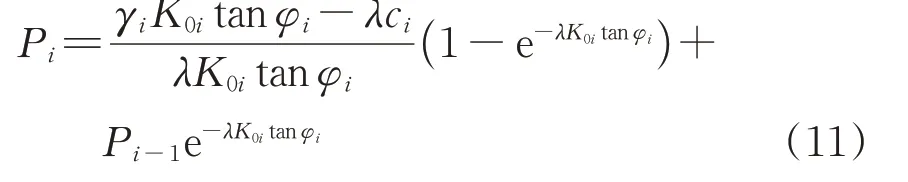
式中：K0i为土层i的静止侧压力系数。

由上述式子进行叠加，可以得到成层土中上覆土压力计算式为

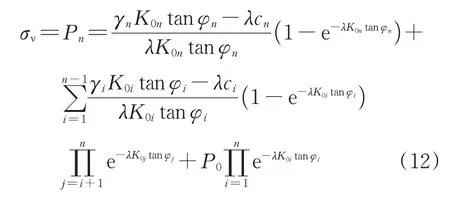
3 工程案例分析

徐州市轨道交通2 号线一期工程周七区间隧道穿越典型的上软下硬地层（地质纵剖面图见图1），本节选用如图11 所示的软土层较厚的剖面进行计算，该处隧道的埋深为17.0 m，上覆土层包括①1杂填土层、②3-3层黏土和⑤3-4层黏土，厚度分别为2.5，2.0 和12.5 m，该剖面各土层的物理力学指标见表2。考虑到①1杂填土层参数缺失，其值取与②3-3层黏土相同。

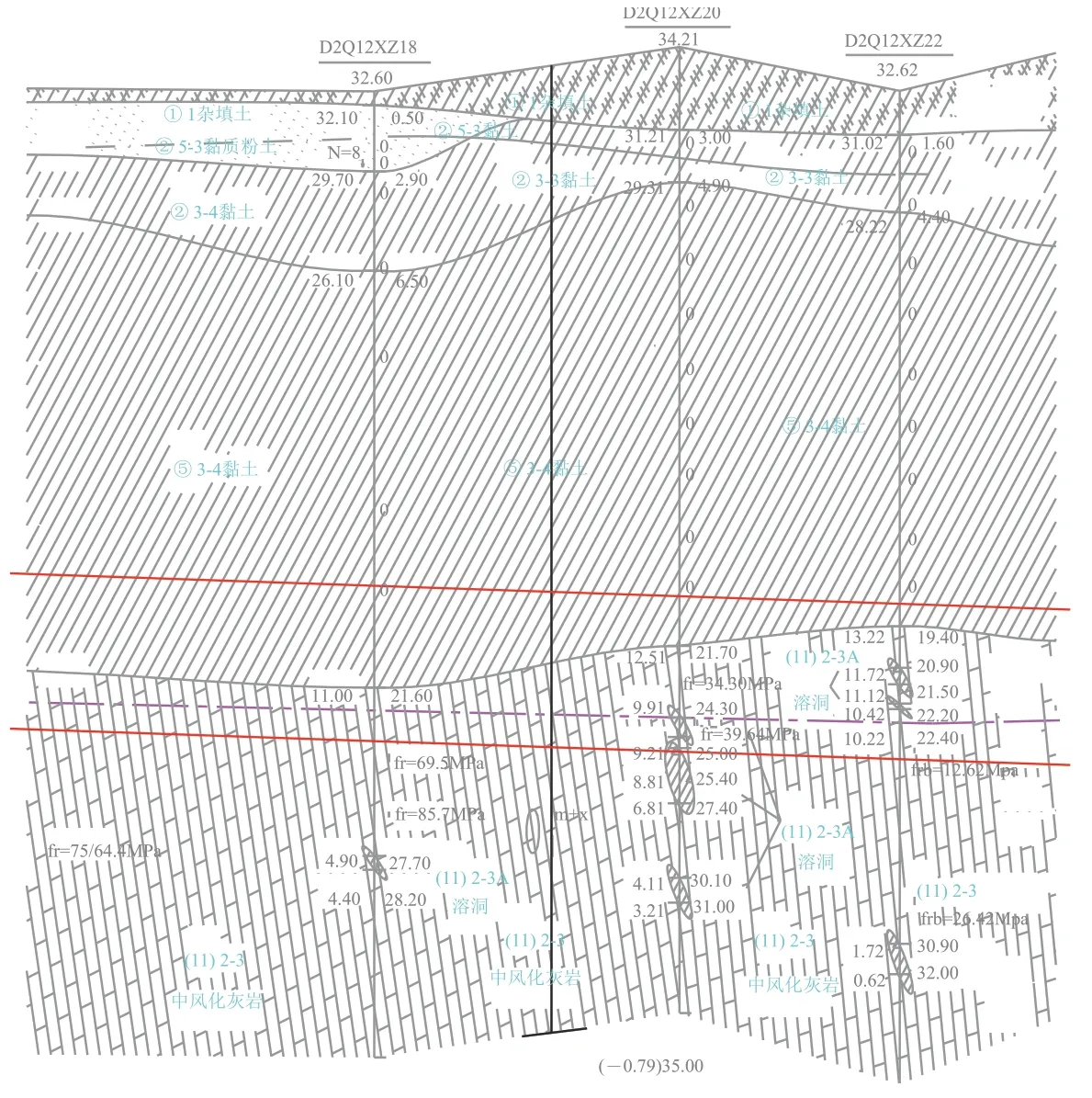
图11 计算地质剖面图

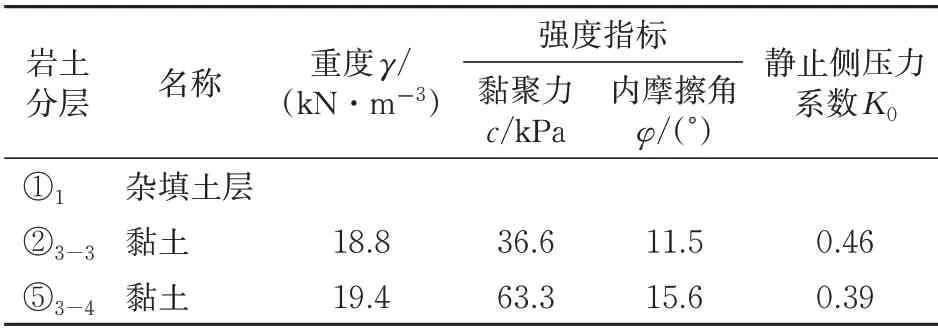
表2 各土层物理力学指标

利用上述方法计算依托工程中软弱地层的临界厚度，即开挖面支护力p=0时的厚度，也即式（7）为0时的l值。令式（7）=0，且α=52.8°，β=50°，φ=15.6°，B=5.5 m，则可计算出ε=0.76。

由于此处地面超载为0，即P0=0，代入式（12）可计算出上覆土压力为

经多次试算，得到l 的临界值为1.5 m，即若无开挖面支护压力，当上部软土层厚度超过1.5 m时即可能发生开挖面失稳破坏。此时，就需要针对性采取应对措施，如对上覆软弱土层进行预加固、优化盾构掘进施工参数或辅助保压措施等。现场施工中，根据该项目计算结果，在上部软土层厚度超过1.5 m 的地方进行地面注浆加固，确保了盾构掘进施工顺利进行，未出现安全事故。

4 结 论

（1）采用三维数值模拟的方法，获得了盾构在上软下硬地层中掘进的变形特性和破坏模式，即变形主要集中在上部软弱地层中，破坏为发生在上部软弱地层中的局部破坏。

（2）在数值模拟结果基础上，通过假定上软下硬地层开挖面部分梯形楔形体破坏模式，推导出的上软下硬地层中上覆土压力计算式和开挖面极限支护压力计算式可应用到实际工程中，并对工程施工起到了指导作用。

（3）根据徐州地铁2 号线周七区间的实际地层情况及隧道埋深情况，计算得到当上部软土层厚度超过1.5 m 时，如无有效支护压力，开挖面即可能发生失稳破坏。针对该情况，现场采取了注浆加固措施，确保了施工安全。