基于理想点法的高速铁路列车停站方案优化

查伟雄，任逸飞，李 剑，严利鑫

（华东交通大学交通运输工程学院，南昌 330013）

列车停站方案是列车开行方案的重要环节，明确列车为旅客提供的服务区间，在列车径路、类别、编组辆数、开行频率确定后，根据客流需求和列车协调配合情况，确定各类列车的停站序列.高铁列车停站越多越方便旅客出行和换乘，也满足旅客的多元化需求，同时可以吸引更多客流，然而停站次数增多也会导致企业运营成本增加，乘客旅行时间增长，也不利于车底周转.因此，合理的停站方案选择对增加铁路企业的效益，提升铁路在多种运输方式中的竞争力有着重大的意义.

从现有的研究来看，国内外学者大多将运输成本最小化作为列车停站方案的目标函数进行考虑.Chang等［1］将铁路企业和旅客出行的成本最小作为目标对台湾列车停站方案进行优化.Qi等［2］以列车空费距离和所有列车总停站数最小为目标建立了一个多目标线性规划模型优化列车停站方案.李得伟等［3］研究了如何使总停站次数最少.也有部分学者考虑到旅客的需求，建立了以旅客出行时间最小为目标的模型来优化列车停站方案.Niu等［4］以旅客总等待时间最小为目标研究了时变条件下一条高铁走廊的列车时刻表优化问题.许若曦等［5］建立了混合整数规划模型，侧重于旅客换乘等待时间损失.牛丰等［6-7］构建不确定客流条件下的高速列车停站方案机会约束规划模型进行研究.田慧欣等［8-9］考虑到城际铁路客流的时变特性，从客流出行时间信息入手，引入时空网络方法，建立了更加完善的评价体系.还有部分学者建立了双层规划模型，将企业和旅客同时进行考虑.邓连波等［10］建立了一个双层规划模型优化旅客列车停站问题.黄志鹏等［11-12］构建了能够描述旅客出行决策和高铁列车开行方案优化的动态博弈过程的双层规划模型.目前大多数学者在进行客流分配的过程中一般采用全有全无法、用户均衡模型或随机用户均衡模型，或将客流量当作约束条件考虑.同时，高速铁路列车停站方案优化为体现停站对经济效益、能力利用、运输组织的难易程度等的影响，采用多目标优化方法更符合实际.但由于量纲、数量级等原因，难点在于目标的集合.

铁路运输具有按流开车、大客流优先的特点，本文结合铁路运输的特点，根据乘客对列车的选择方式，即乘客会选择在途时间最短的列车，提出了一种适用于铁路的客流分配方式，并命名为大客流优先分配法.将客流分配到每一列列车上，为停站方案制定、开行方案制定、客票分配等环节奠定基础.同时建立了以列车总停站次数、列车空费能力、旅客时间损失最小为目标，满足客流、列车运输能力、每辆列车停站次数、始发终到站及重点车站停站约束的多目标高速铁路列车停站方案优化模型，并设计了以理想点法为适应度函数的改进遗传算法进行求解，通过实例验证了模型及算法的可行性.

1 高速铁路列车停站方案数学描述

高速铁路列车停站方案是高速铁路列车在列车径路、类别、编组辆数、开行频率确定后，在各站点是否停站的停站序列［13］.本文主要以直线型多始发终到站列车停站方案为研究对象.设S={Si|i=1，2，…，n}为某高速铁路线路上的车站集，n表示线路上的车站总数.T={Tk|k=1，2，…，m}为线路中的列车集，m表示线路上的列车总数.高速铁路线路示意图如图1 所示.

图1 高速铁路线路示意图Fig.1 Schematic diagram of high-speed railway line

对于不同的列车Tk，它们的编组辆数不尽相同，用Gk表示高速铁路列车编组辆数.高速铁路列车编组辆数大多为8 节或16 节.不同的编组辆数也对应着不同的列车运输能力，往往用额定载客量来描述列车运输能力，用ck表示列车Tk的额定载客量.

引入0-1 变量xk，i来描述列车Tk在车站Si停与不停两种情况，若列车Tk在车站Si停，则xk，i=1，若列车Tk在车站Si不停，则xk，i=0.

通常，一条线路上的列车停站方案包括一个以上的列车开行区段，对于不同开行区段的列车，它们的始发站和终到站不同，用sk表示列车Tk的始发站，用ek表示列车Tk的终到站.即当Si=sk或Si=ek时，xk，i=1.用Rk表示列车Tk的开行区段，而不在开行区段中的车站，对于列车Tk来说，不存在停站作业，即当Si∉Rk时，xk，i=0.

2 高速铁路列车停站方案优化模型

2.1 模型假设

直线型高速铁路停站方案的影响因素较多［14］，在建立模型之前，须做如下假设：

1）相同性假设.假定双向线路的客流量和收益相同，若要使整条线路的收益最大，只需要对单向线路进行研究.

2）确定性假设.列车的起讫点、开行对数、开行时间、动车组编组、动车组周转运用情况及客流均为已知条件，不考虑由于所制定的停站方案的不同所带来的客流量的变化.

2.2 目标函数设计

1）停站总次数最少.

增加列车停站次数将延长列车占用车底的时间.因此，在满足旅客需求的前提下，尽量减少列车停站次数，可以降低运输成本，提高铁路企业经济效益.因此，以停站总次数最小为第一个优化目标建立目标函数为

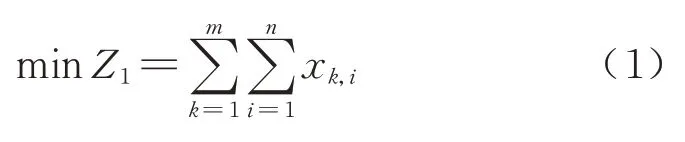
2）列车空费能力最小.

铁路集团在制定列车停站方案时会保证列车的上座率达到一定标准，列车空费能力在某种程度上可以表示列车座位浪费情况，用站间空座位数与站间距离的乘积表示为

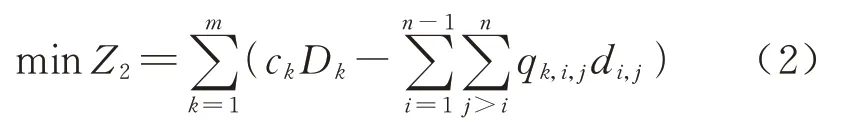
式中：Dk为列车Tk运行距离，km；qk，i，j为列车Tk上从车站Si到车站Sj的旅客数量；di，j为车站Si和车站Sj之间的距离.

3）旅客时间损失最小.

旅客在途时间由旅客候车时间、列车运行时间和列车停站消耗时间构成.本文主要考虑列车停站消耗时间对旅客时间损失的影响，因此旅客时间损失为不下车的旅客由于列车停站而增加的旅行时间，计算公式为

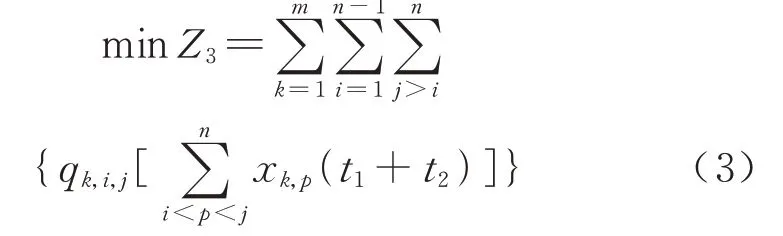
式中：车站Sp为车站Si和车站Sj中间的车站；t1为列车的停站时间，min；t2为列车的启停附加时间，min.

2.3 约束条件设计

列车停站方案必须尽可能满足铁路运输需求并符合相关技术规范.因此，在编制过程中需要考虑一系列系统约束条件，如客流需求约束、列车运输能力约束、每辆列车停站次数约束、始发终到站及重点车站停站约束等.

1）客流量约束.

停站方案的编制需遵从按流开车的原则［15］，即根据客流量的多少，确定列车是否进行停站服务.因此，各区段上列车的载客数量都应该满足区段客流的需求，以尽可能地保证客流能够全部带走.约束条件为

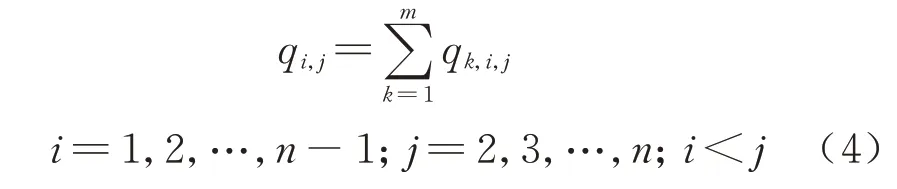
式中：qi，j为从车站Si到车站Sj的客流 量.

2）列车运输能力约束.

为保证高速铁路列车的服务质量和服务安全，需要保证在任何时候，高速铁路列车上的旅客数量均不大于列车的定员数，即每个区间列车上的人数均不大于列车的定员.

设n个车站将高速铁路线路分为n-1 个区间r，约束条件为

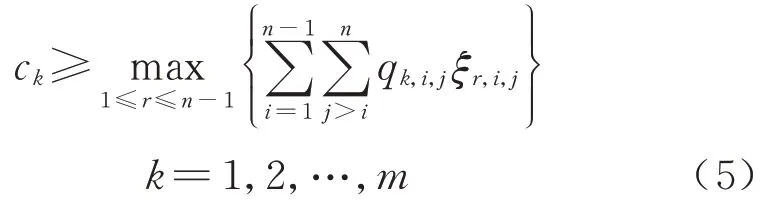
式中：ξr，i，j为0-1 变量，表示区间r是否在车站Si和车站Sj之间.

3）每辆列车停站次数约束.

列车停站次数过多会降低列车的旅行速度，同时影响了通过能力.为满足旅客对便利性、快捷性、高服务质量以及铁路部门经济效益、运输效率等不同方面的要求，需要对单次列车最大停站次数进行限制.同时为满足必须的停站作业需求，需要对单次列车最小停站次数进行限制.约束条件为

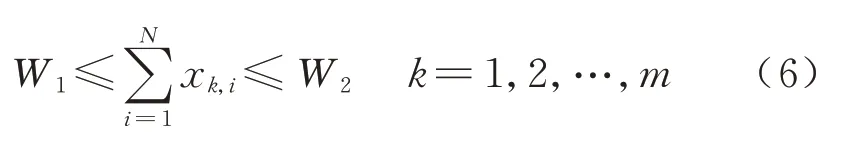
式中：W1为列车Tk的最小规定停站次数；W2为列车Tk的最大规定停站次数.

4）始发终到站及重点车站停站约束.

通常一条线路上的列车停站方案包括一个以上的列车开行区段，对于不同开行区段的列车，它们的始发站和终到站不同，列车在其始发终到站必须停车，同时为满足必要的停站作业，在某些列车在相应的重点车站也必须停车.对于列车Tk，不在其开行区段中的车站，不存在停站作业，约束条件为

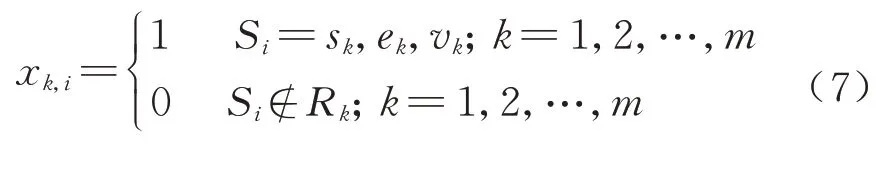
式中：vk为列车Tk的重点车站.

5）取值范围约束.

变量xk，i描述列车Tk在车站Si停与不停两种情况，是0-1 决策变量，取值范围为

变量qk，i，j取值范围为

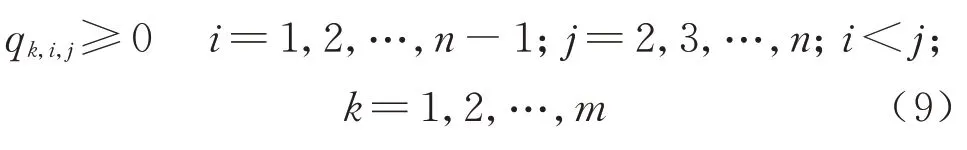
变量ck为列车Tk的额定载客量，为方便计算，高速铁路8 节编组列车的额定载客量通常取600，16 节编组列车的额定载客量通常取1 200，取值范围为

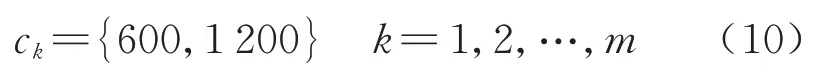
2.4 优化模型分析

通过对目标函数和约束条件的设计，得到高速铁路停站方案优化模型，该模型为多目标0-1 非线性优化模型，属于NP-hard 问题，使用精确算法很难在较短时间内获得最优解，因此选择了人工智能算法来对其进行求解.

3 算法设计

针对模型，首先需要进行客流分配来确定每列列车上乘客的上下站点，才能对目标进行求解.结合0-1 决策变量以及列车停站方案的特点，该模型适合用遗传算法求解.本文利用理想点法将多目标问题转化为单目标问题，并设计了结合大客流优先分配法的遗传算法对模型进行求解.

3.1 大客流优先分配法

铁路上的客流分配方式与道路上的客流分配方式不同，若把选择不同的列车看作选择路径，路段的阻抗不是随着客流增加而慢慢变化的，而是当乘客数到达额定载客量时，后续的乘客就不能选择乘坐这趟列车.因此不能采取常规的如用户均衡等配流方法.

本文结合铁路运输按流开车、大客流优先的特点，根据乘客对列车的选择方式，即乘客会选择在途时间最短的列车，提出了一种适用于铁路的客流分配方式，并命名为大客流优先分配法.具体算法思路为：根据按流开车的原则、开行方案的编制原则以及客票分配的原则，可以将客流数量最多的OD 点对的乘客优先分配满足乘客上下车、中途停站最少以及运行总里程最短的列车.根据客流数量大小依次分配，最后将所有客流分配完毕.

客流分配方式的具体算法分为4 个步骤.

步骤1：在客流OD 矩阵中选取数值最大的数a，a对应了从车站Si到车站Sj的旅客数量.

步骤2：在事先生成的0-1 停站矩阵中选取满足xk，i=1和xk，j=1且尚未满员的列车，累加列车从i站到j站的停站0-1 变量，选取其中累加值最小的一列列车或几列列车，也就是从车站Si到车站Sj中间停站次数最少的列车.

步骤3：计算这几列列车的行驶里程长度，选取其中行驶里程数最短的一列或几列列车，若是一列列车，将该列车额定载客量减去车站Si到车站Sj之间各区间的已有载客量，取最小值；若是几列列车，将分别计算这几列列车额定载客量减去该列车从车站Si到车站Sj之间各区间的已有载客量，取最小值.

步骤4：若待分配的客流数量小于此最小值，则将待分配的客流数量全部附加到该列车上或几列列车上，将客流OD 矩阵中的对应客流清零，并转回步骤1 进行下一次分配.若待分配的客流数量大于等于此最小值，则将该最小值的客流附加到列车上.将客流OD 矩阵中的客流减去已经分配下去的客流，并转回步骤1 进行下一次分配，若最后=0，则说明该停站方案满足客流需求.若最后qi，j-＞0，则说明该停站方案不合理.

3.2 理想点法

由于设计的优化模型存在多个目标，且目标的单位和数量级具有较大差异，一般的权重赋值方法并不适用于将此多目标问题转化为单目标问题，理想点法具有可以无视不同目标之间单位和数量级差异的优点，因此本文引入理想点法作为适应度函数，具体计算方法为：在相同的约束条件下，对多目标问题中的各个目标单独进行求解，得到各个目标的最优解

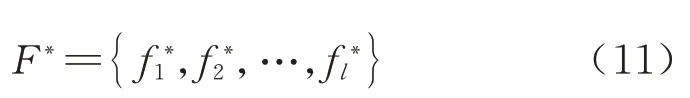
引入惩罚因子αl，对于每一种停站方案都有一个实际值F={f1，f2，…，fl}，将实际值和期望值之间的偏差做比较来选择问题的解，其数学表达式为

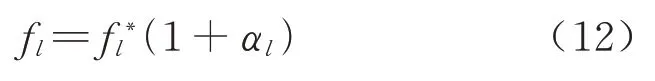
取适应度函数的最小值，转化后的单目标问题的解即为原多目标问题的解

在本文中，由于多目标优化的目标数为3 个，因此l=1，2，3，对各目标代入下文遗传算法进行单目标求解，计算出期望值，各目标期望值分别为f1=438，f2=35 557 627，f3=706 390.

3.3 遗传算法设计

遗传算法的基础思想就是先编码，然后再随机地生成初始的种群.以优胜劣汰为基础原则，根据目标函数值所设定的适应度函数，在群体中通过选取适应度最好的个体直接从其中进入下一代，邻域群体则是通过交叉变异而产生的，而且在其中存活下来的后代则是经过自然选择后目前在该种群中最好的染色体.具体算法分为9 个步骤.

步骤1：初始化，包括初始停站方案相关数据，车站数据、列车数据、客流数据等以及遗传算法的交叉概率、变异概率、种群规模、最大迭代次数.

步骤2：种群初始化.初始化种群P，种群大小为N.每一个个体代表一个列车停站方案.由于使用0和1 表示列车在车站是否停站，所以采用二进制编码.以高速铁路线上所有列车经过的站点为一个染色体，一个站点作为一个基因位，所有站点的集合就是染色体的长度.基因取值为0 表示列车在该站不停站，取值为1 表示列车在该站停站.

步骤3：客流分配.运用大客流优先分配法，将所有乘客分配到每一列列车上，若个体不满足客流需求，则在适应度计算时加一个较大惩罚因子，若满足客流需求，则进入下一算法步骤.

步骤4：适应度函数设定.运用理想点法将多目标问题转化为单目标问题.求解每个目标的最优解作为期望值，通过比较实际值和期望值之间的偏差对个体从小到大进行排序.

步骤5：判断是否达到最大迭代次数，若没有，则继续下面的算法步骤.若达到最大迭代次数，则输出个体适应度值最低的最佳个体作为结果.

步骤6：以适应度函数的大小为依据，对群体进行排序，采取锦标赛选择，产生新一代种群.

步骤7：对种群中的染色体进行交叉操作，根据交叉概率随机选择2 条染色体，采用两点交叉将2 条染色体对应序列的基因进行交换.

步骤8：对种群中的染色体进行变异操作，根据变异概率随机选择染色体，采用单点变异随机生成新个体.

步骤9：经过选择、交叉、变异后生成的新种群，转向步骤3 进行计算.

4 算例分析

以京沪高铁2018 年某日列车停站方案相关资料为例进行分析，京沪高速铁路由北京南站至上海虹桥站，全长1 318 km，共设24 个车站，为方便计算，将天津西站和天津南站都统计为天津站，统计为23 个站.23 个车站将线路划分为22 个区间，将车站沿下行方向依次标号如图2 所示.

图2 京沪高铁线路示意图Fig.2 Schematic diagram of Beijing-Shanghai high-speed railway line

初始停站方案中列车总数m=62 列.各列车始发终到站均确定.停站时间t1=2 min，启停附加时间为t2=3 min.编组辆数均为16 辆，列车定员ck=1 200 人.最小停站次数W1=2，最大停站次数W2=16.客流数据见表1.

表1 2018 年某日京沪高铁下行列车客流表Tab.1 Passenger flow chart of Beijing-Shanghai high-speed railway on a certain date in 2018

4.1 计算过程

为验证算法的有效性，采用电脑CPU 为2.6 GHz六核Intel Core i7，内存为16 GB，MATLAB 2019 b 进行求解，参数设置：最大迭代次数500 次，初始种群规模为100，交叉概率为0.8，变异概率为0.2，先对各目标进行单目标求解，计算出期望值，各目标期望值分别为f1=438，f2=35 557 627，f3=706 390.再利用理想点法求解得到优化后的京沪高铁列车停站方案.迭代次数图如图3所示.

由图3 可见，算法在第346 代后趋于稳定，转化后的单目标问题最小值为0.111.优化后的列车停站方案如图4 所示.

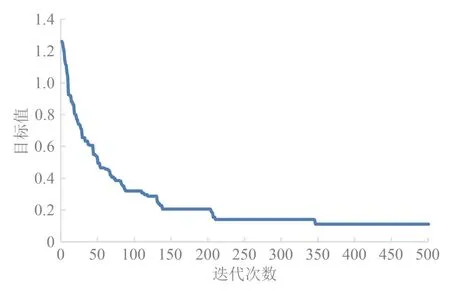
图3 迭代次数图Fig.3 Schematic diagram showing numbers of iterations

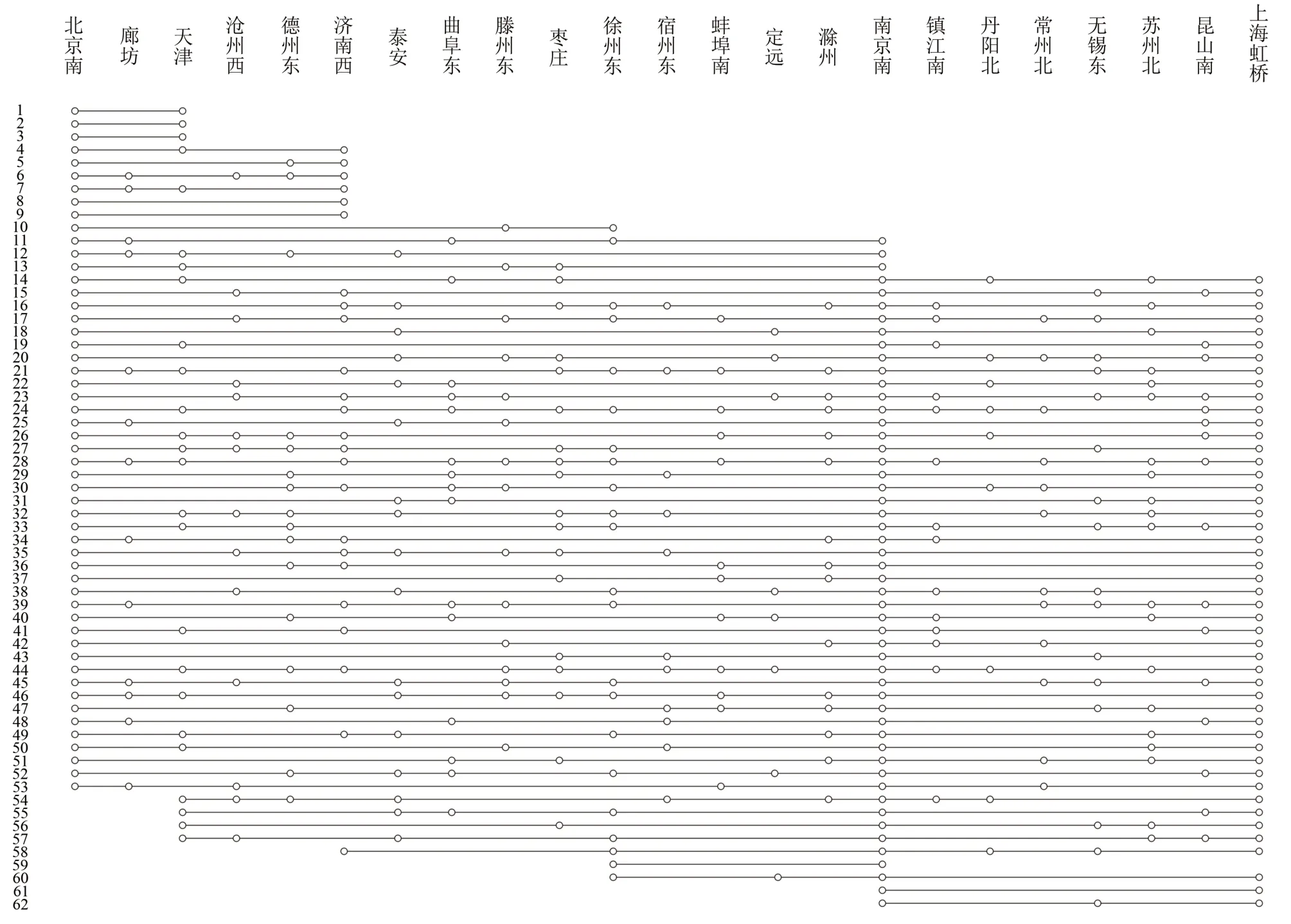
图4 优化后的列车停站方案图Fig.4 Schematic diagram of optimized schedule for train stops

4.2 结果分析

将得到的优化后的列车停站方案与现有列车停站方案在几个方面做比较，结果如表2 所示.

由表2 可知，该列车停站方案的总停站次数为465 次，优化前的原始停站方案的总停站次数为505 次，减少了40 次，优化了7.92%.该列车停站方案的列车空费能力为36 257 241，优化前的原始停站方案的列车空费能力为45 236 534，减少了8 979 293，优化了19.84%.该列车停站方案的旅客损失时间为727 065 min，优化前的原始停站方案的旅客损失时间为1 243 400 min，减少了516 335 min，优化了41.52%.

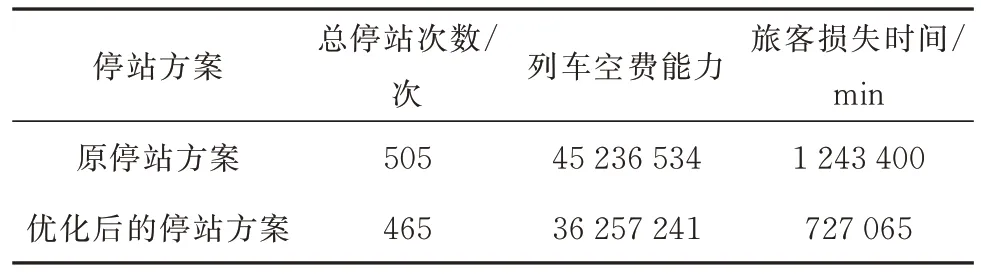
表2 列车停站方案对比表Tab.2 Comparison of train stop schedule

研究结果显示，相比较于原列车停站方案，新的列车停站方案在各方面都有所改进.针对总停站次数和列车空费能力的优化效果并没有旅客损失时间那么显著，是因为提出的一种新的客流分配方法，可以极大程度地减少旅客因停站而损耗的时间，而为了满足客流的出行需求，有些停站是必须的，所以针对列车总停站次数的优化效果没有那么明显，但是也减少了不必要的停站.因此，研究成果可为列车停站方案的制定提供合理参考.

5 结论

1）建立了以总停站次数、列车空费能力、旅客损失时间最小为目标函数的多目标列车停站方案优化模型.并提出大客流优先分配法，设计了遗传算法对模型进行求解.

2）以京沪高铁为实例，对原列车停站方案进行优化.结果表明，优化后的列车停站方案能够减少7.92%的停站次数，减少19.84%的列车空费能力，降低41.52%的旅客损失时间，研究成果可为停站方案的制定提供合理参考.

3）以直线性列车停站方案作为研究对象，很多条件已经确定，复杂度较低.下一步研究方向是继续完善客流分配方式，以及结合客流分配的高速铁路开行方案优化.