基于tripling的补设计的性质研究

黄兴友，薛慧丽，李洪毅

吉首大学数学与统计学院，湖南 吉首 416000

0 引言

Doubling方法最初被用来构造正交主效应设计[1].文献[2]讨论了用一个分辨度为Ⅳ的二水平正规部分因析设计，通过doubling方法来构造分辨度仍为Ⅳ的Double设计，随后doubling的方法在设计的构造中得到了广泛的应用[3-5].文献[6-7]对于二水平的Double设计与初始设计之间的示性函数及在各种最优准则下的联系进行了深入研究.文献[8]以水平置换作为折叠反转方式提出用tripling方法构造三水平Triple设计，构造了一系列具有最小低阶混杂的三水平因子设计.文献[9]进一步讨论了Triple设计和其初始设计在广义最小低阶混杂准则、最小低阶矩混杂准则及均匀性准则下的解析联系.

1 基本概念

记U(n；3s)为一类具有n次试验，s个三水平因子的U-型设计，即每个因子出现的水平次数相同.设D∈U(n；3s)，其可以看成是n×s矩阵D=(xil)n×s，xil=0，1，2，i=1，2，…，n，l=1，2，…，s，D的每一行对应一次试验，每一列对应一个因子.

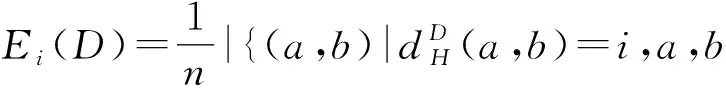
(1)

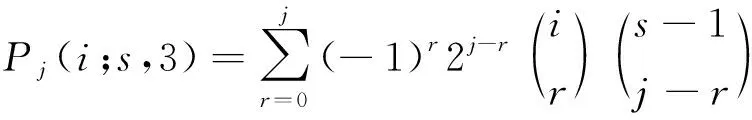
根据Krawtchouk多项式的正交性，易得

(2)

偏差作为设计的均匀性度量已在许多文献中使用，本文选取可卷型L2-偏差来衡量设计的均匀性，为方便起见，用WD表示.对于任意设计D∈U(n；3s)，它的WD值平方可通过公式计算：

(3)

其中uil=(2xil+1)/6，i=1，…，n，l=1，…，s.

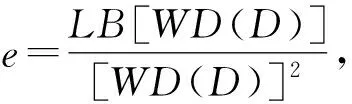
设D∈U(n；3s)，表1列出了D∈U(n；3s)的所有水平置换方式及置换设计.

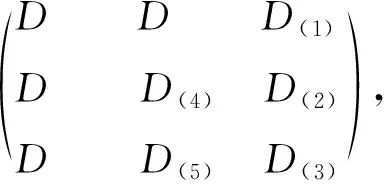
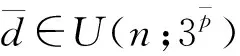
表1 设计D的6种水平置换方式及置换设计

2 主要结论

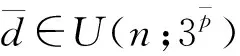
证明根据(2)式和文献[8]中引理1有

由(2)式有

结论得证.

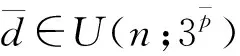
(4)

其中：

证明当p≡0(mod 3)时，由(1)式和文献[9]引理1，对于1≤j≤3p有

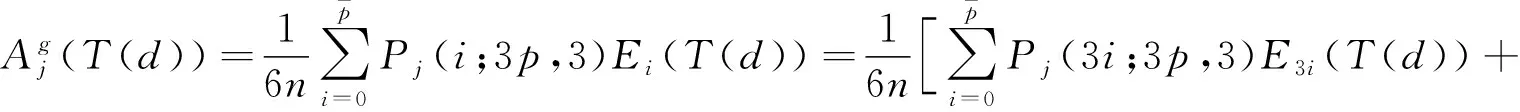
根据(2)式和文献[13]引理1有

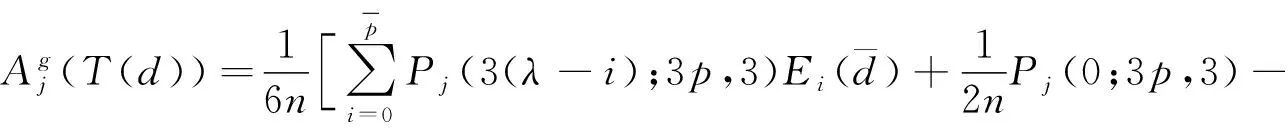
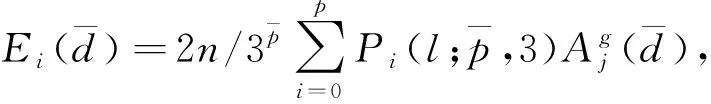
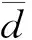
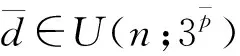
(5)

(6)

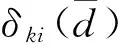
(7)

(8)

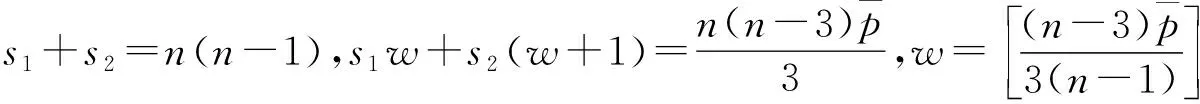
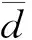
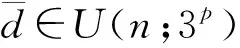
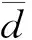
3 数值例子

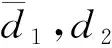
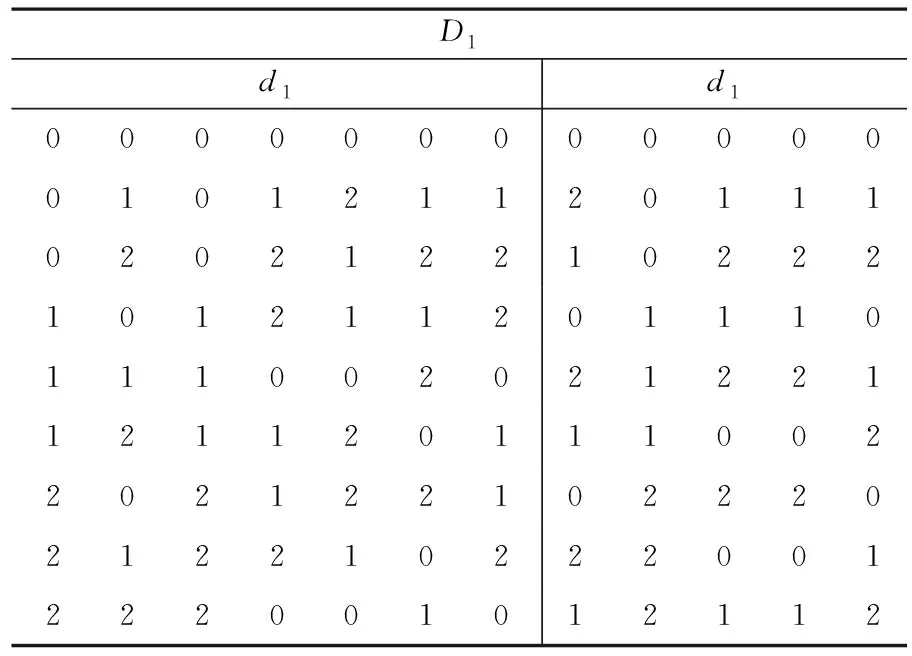
表2 三水平等距设计D1∈U(9；312，9)

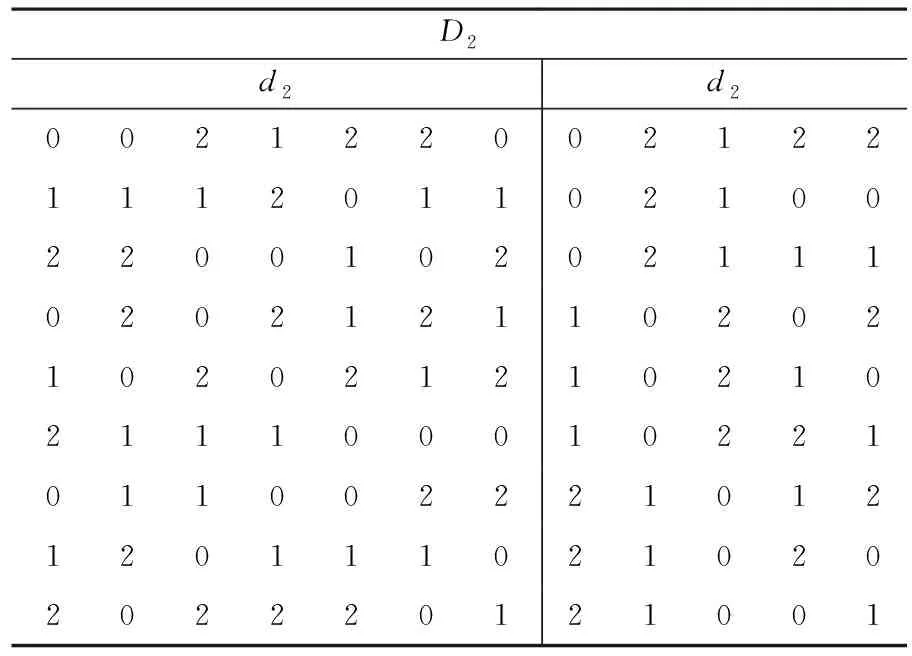
表3 三水平等距设计D2∈U(9；312，9)

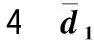
表和的广义字长型模式

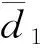
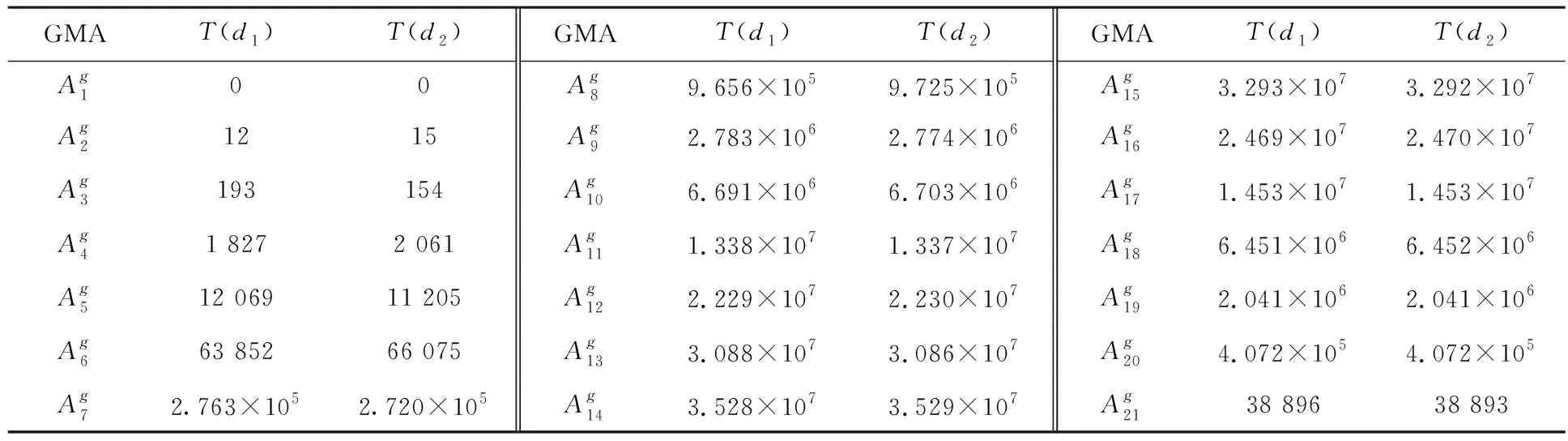
表5 Triple设计T(d1)和T(d2)的广义字长型模式

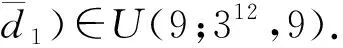
4 结语