“点的合成运动”教学实践与探索

范旭红 王自平

(江苏大学土木工程与力学学院 江苏镇江 212013)

理论力学课程中“点的运动学”是研究一般物体的基础，该章研究点的简单运动，主要研究点相对某一个参考系的几何位置随着时间变化的规律，包括点的运动方程、运动轨迹、速度和加速度，这部分知识点比较简单，学生根据建立的运动方程求导就可以求出速度等加速度，其实就是高等数学里面涉及的求导数的问题。关于刚体的简单运动，这部分知识在大学物理这门课也有涉及，所以学生对刚体的平动和定轴转动也并不陌生，分析物体相对于不同参考系运动之间的关系可以称为复杂运动，这两章内容的学习为点的复杂运动做了很好的铺垫。

“人不能两次踏进同一条河流”是古希腊哲学家赫拉克利特的观点，在这个哲学观点里面强调运动是绝对的，静止是相对的，世界的万事万物都处在一个运动变化的过程中，而静止只是相对某一个参考物体的静止，没有绝对的静止。事实上，该哲学观点等同于力学问题中运动的描述。一个研究对象它的运动规律是什么样的，必须指出它的参考系，同一个研究对象对于不同的参考系来说运动的描述是不同的，前面两章“点的运动学”和“刚体的简单运动”都是相对于一个定参考系的运动，属于简单的运动，物体相对于不同参考系的运动是不同的，它们之间有一定的关系，研究物体对于不同参考系之间的关系称为复杂运动或者称之为合成运动，这也是该章涉及的内容—点的合成运动[1-2]。这部分内容是学生在该章中感觉很难理解和应用的内容，特别是在解题的时候很多初学者不知所措。

为了描述它们之间的关系，学生必须明确采用动点和不同的参考系来描述3种运动。

1 理解“一点二系三运动”

首先定义两个参考系，即定参考系和动参考系，定参考系是指把参考系固结在相对于地球不动的物体上的参考系，习惯上把固结在地球上的参考系称为定参考系简称定系，以(oxyz)表示，固定在其他相对于地球运动的参考体上的参考系称为动参考系简称动系,以(o'x'y'z')表示[3]，有了参考系就可以定义3种运动[4]，动点相对于定参考系的运动叫绝对运动，动点相对于动参考系的运动叫作相对运动，动参考系相对于定参考系的运动叫作牵连的运动。特别需要注意的是，绝对运动和相对运动是点的运动，牵连运动是动参考系相对于静参考系的运动，是刚体的运动。点在某瞬时的绝对速度等于相对速度和牵连速度的矢量和，这是点的速度合成定理[5]，点在某瞬时的绝对加速度等于相对加速度、牵连加速度和科氏加速度的矢量和，这是点的加速度合成定理[6]。必须特别注意由于动参考系的运动是刚体的运动而不是一个点的运动，所以除非动参考系作平动否则其上各点的运动不完全相同，在动参考系上与动点相重合的那点（牵连点）的速度和加速度称为动点的牵连速度和牵连加速度[7]，其中牵连速度和牵连加速度比较难理解，这点非常重要，是需要在课堂中重点讲解的内容，以便于学生熟悉和理解这些概念；其次很关键的问题是针对实际问题如何选择合适的动点和动参考系。

2 动点、动系选择实践

动点动系的选择对于学生解题非常重要，也是该章的关键问题，如何选择呢？通过多年的教学实践，归纳如下。

（1）有个明显的动点在题目中很容易发现（一般为题目中的研究对象）；（2）有一个不变的接触点，可以选择该点为动点；（3）若没有不变的接触点，此时应该选择相对轨迹容易确定的点为动点；（4）有时候根据题意需要选择两次动系。

依据这些原则，可以发现动点、动参考系和定参考系分别在3 个不同的物体上，一般来说动点是两个机构的接触点，而且动点是唯一的不变的一个对象；其次机构中动点对于动参考系的相对轨迹明显简单，要么是直线要么是圆弧，这是一个非常重要的原则，根据以上原则，可以对很多的问题有正确的判断和分析。再者，根据经验，对于滑块式连接，滑块就是需要选择的动点，滑道就是固结动系的物体，滑套式的连接，滑套就是大家需要选择的动点，滑套在哪个杆件上滑动，这个杆件就是固结动系的物体。下面针对具体问题举例分析。

根据图1图形可知，OA杆和滑道两个机构接触点就是滑块，所以滑块A就是动点，ABC滑道就是固结动参考系的物体，绝对运动是以OA为半径的圆周运动，相对运动以O1A为半径的圆弧，牵连运动是ABC的平动，牵连点是滑块和滑道重合的那个点，该点的速度和滑道ABC相同，因为动参考系做平动。

图1 案例1

根据图2 图形可知，OA和AB两个机构的接触点就是滑套A，所以滑套就是动点，OC就是固结动系的物体，绝对运动是上下的直线运动，相对运动是滑套A沿着OC的直线运动，牵连运动是定轴转动，牵连点是滑套和OC重合的那个点，该点的速度等于ω·OA。

根据图3 图形可知，这个实例比较特殊[8]，对于动点，既不能取AB上的点，也不能取轮子上的点，因为不同的瞬时轮子和AB滑道上不同的点接触，不满足动点的唯一性的规则，通过认真观察该机构，看看相对运动的情况，由于顶杆始终接触凸轮表面，大家不难发现动点C到滑道AB的相对距离一直不变，也就是相对运动是一条平行于滑道的直线，所以点C就是选择的动点，AB滑道就是固结动系的物体，动系平动，绝对运动是以OC为半径的圆，相对运动是平行于顶杆底边的平行线，牵连运动是上下的平动，这里大家一定要注意牵连点，牵连点是C点和参考系重合的点，而不是和顶杆重合的点，由于动系平动，牵连速度和顶杆相同，有同学对于这点有点迷惑，所以一定要讲清楚参考系和参考体的概念，参考系是无限大的空间，而参考体是个有限大的物体，把握住牵连点不一定在参考体上，但是在参考系上，参考系和参考体运动方式是相同的，教师可以借助于该题把牵连速度的概念讲透彻。

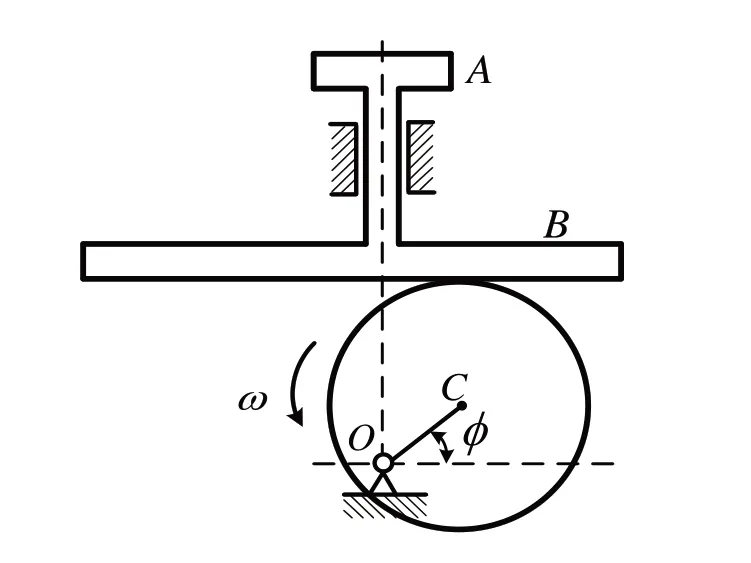
图3 案例3

3 典型案例分析在实践教学中的探索

一般情况下动点动系确定后先进行速度分析，速度分析的时候特别要注意若动系平动是没有科氏加速度，若动系转动在速度分析的时候一定要算出相对速度的大小，标注出相对速度的方向，便于计算科氏加速度大小和画出科氏加速度方向。图4为直杆滑动的案例，图示直角弯杆OBC绕O转动，使得小环M沿着固定直杆OA滑动，已知OB=0.1 m，OB和BC垂直，曲杆的角速度ω=0.5 rad/s，角加速度为0，求当ϕ=60o时，小环M的速度和加速度。

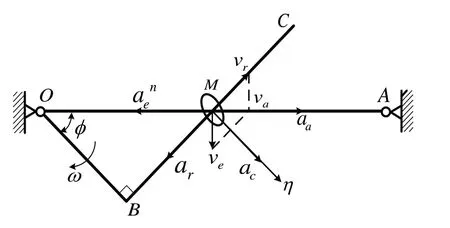
图4 案例4

机构运动分析，小环M为动点，OA不动，M沿着OA的运动是绝对运动，绝对运动为直线运动，动系固结在OBC上，动系做定轴转动，M相对OBC是沿着BC的滑动，相对运动轨迹非常明显，（相对运动也是直线），动参考系相对于定参考系运动是牵连运动，牵连运动为定轴转动，需要注意的是：运动分析的时候要计算相对速度，以便于后面确定科氏加速度大小和方向的时候用到。牵连点和弯杆OBC的M点重合，所以牵连速度是垂直于OM的，大小等于ω·OM。

3.1 速度计算分析

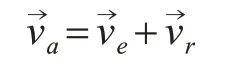
其中绝对速度大小未知方向水平，相对速度大小未知方向沿着MC，牵连速度方向垂直OM，大小等于ω·OM，容易解出：va=0.1723 m/s，vr=0.2 m/s。

3.2 加速度计算分析

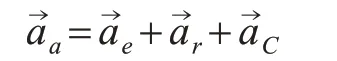
其中绝对加速度大小未知，方向沿着MA，牵连加速度大小方向都确定，大小等于OM·ω2，方向沿着MO，相对加速度大小未知，方向沿着MC，科氏加速度大小和方向按照右手法则确定，大小为2ω×vr，方向见图4，把该矢量表达式向η轴投影得

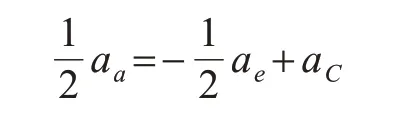
解出：aa=0.35 m/s2。

该题在教学过程中会出现两个问题，一个是牵连速度的判断，很多学生会在牵连速度的方向确认上有问题，这里需要掌握牵连点的概念，M环和OBC重合的那个点的速度，该瞬时在垂直于OM的方向，大小等于ω乘以OM，其次是由于动系做定轴转动所以有科氏加速度，科氏加速度等于2ω×vr，方向用右手法则判断，在科氏加速度方向的判定时，适当多举例，多练习，一定注意方向不能画错了，不然就会造成结果的错误。同时，可以观察到动点、动系、静系分别在3 个不同的物体上，使得3 种容易分解，特别是相对运动明显简单。

4 结语

通过“点的合成运动”的实践与探索可知，动点和动系的正确选择是解题正确的关键所在，另外就是关于牵连点的理解，牵连速度不是动点的速度，而是动系上和动点重合的点的速度，其次就是解题过程中速度图和加速图要正确画出来，如果图错了，那么就谈不上正确的结果了。要求学生尽量采用列表的方式，不仅仅表达出矢量的大小也有方向，未知量一目了然，最后就是选择合适的投影轴，求出未知量。该章除了课堂教学之外，也要让学生适当地多分析一些例题，加强他们对概念的理解，以便于达到良好的课堂教学效果。同时可以带领学生做简单的机构运动的教具，通过亲自做教具实实在在地观察3 种运动的真实情况，从而深刻理解“点的合成运动”的概念，达到该章所期望的教学效果。