带重要点约束的经典轨迹相似度量新算法*
王前东,谢 卫
(中国西南电子技术研究所 成都 610036)
0 引 言
随着战场监视手段的应用和发展,大量目标被发现、监视和跟踪,每天获取的轨迹数量不断增加,积累的轨迹体量呈爆炸式增长,用户所关心的信息常常被海量的不相关信息淹没,需要对大量的目标活动轨迹进行规律发现和总结。经典轨迹便是这种活动轨迹规律的总结[1-3]:从大量时空轨迹里发现关注目标的频繁路径。实时轨迹是目标当天飞行的实时路径。通过实时轨迹与经典轨迹进行比较,判断实时轨迹与哪条经典轨迹相似,从而分析目标的行为意图或异常活动情况[4]。因此,实时轨迹与经典轨迹的相似性度量是目标监视任务中重要的关键技术之一。
轨迹的相似性度量主要用轨迹间的距离来表示。不同应用场景要求的轨迹距离不同[5]。对于没有带重要点约束的经典轨迹相似轨迹判断问题已有解决办法,解决的核心思想主要有欧氏距离、Hausdorff距离、动态时间弯曲距离、Frechet距离、最长公共子序列等。由于实时轨迹存在强噪声、部分轨迹点漏侦、轨迹断裂等异常情况,轨迹相似度量主要采用最长公共子序列长度算法[6]。文献[7]证明了最长公共子序列长度算法的轨迹相似判断增强了算法鲁棒性,但该算法未考虑重要点约束的影响。
经典轨迹中关注目标每次出行活动比较规律、在某些重要点具有重要的行为意图,这些重要点包含特殊的语义,是寻找相似轨迹的重要关注点。文献[8]利用加权的动态时间弯曲距离算法进行处理,实现了对不同点权重不一样的轨迹相似度量,但没有针对指定的重要点赋予权重,不能处理带强噪声的轨迹相似度量。针对带重要点约束和轨迹中的强噪声,本文定义了一种新的带重要点约束的轨迹相似度量模型。该模型中定义了三条轨迹:经典轨迹和实时轨迹为待判断的两轨迹,重要点轨迹为约束轨迹。如果实时轨迹为带重要点约束的经典轨迹的相似轨迹,则实时轨迹必须满足条件:实时轨迹是经典轨迹的相似轨迹;重要点是经典轨迹的子轨迹;重要点是实时轨迹的子轨迹。
本文针对这种带重要点约束的经典轨迹的相似度量模型,借助文献[7]中将最长公共字串长度算法应用于轨迹相似度量的思想,将带约束的最长公共子序列长度算法[9]和带匹配路径约束的最长公共子序列长度算法[10]应用于经典轨迹的相似度量,分别提出了带重要点约束的经典轨迹相似度量基础算法和带重要点约束的经典轨迹相似度量快速算法(带匹配路径约束的经典轨迹相似度量新算法)。
1 最长公共子轨迹的经典轨迹相似度量算法
定义1最长公共子轨迹(Longest Common Subtrajectory,LCS)
设经典轨迹Cm=(c1,…,ci,…,cm)与实时轨迹Qn=(q1,…,qj,…,qn)的公共子轨迹为Zr=(z1,z2,…,zr),则Zr必须满足
(1)
式中:ε为距离阈值,dis(zs,qvs)为zs与qvs两点之间的欧氏距离。
Zr为两轨迹Cm与Qn的LCS,当且仅当Zr为满足式(1)条件中点数最多的轨迹。
令ε>0为距离阈值,L1ε(m,n)为经典轨迹Cm与实时轨迹Qn的LCS长度,根据LCS定义,有如式(2)所示的LCS长度计算的递推公式L1ε(i,j)[6]:
(2)
计算L1的初始值:对任意i≥0,L1ε(i,0)=0;对任意j≥0,L1ε(0,j)=0。
令f1为经典轨迹Cm与实时轨迹Qn的轨迹相似度,则f1可由式(3)所示的公式求出:
(3)
上述公式为基于LCS的经典轨迹相似度量算法,简称LCS算法。f1ε(Cm,Qn)计算的时空复杂度为O(mn)。
2 带重要点约束的经典轨迹相似度量新算法
令Cm为经典知识库中保存的一条经典轨迹,Cm=(c1,…,ci,…,cm)为m个轨迹点按时间由小到大排列成的序列,其中ci=(cx,i,cy,i)为经典轨迹Cm中的第i点位置坐标。设Pt=(p1,p2,…,pt)=(ci1,ci2,…,cit)为经典轨迹Cm中指定的重要点,且重要点在经典轨迹中的位置序列为It=(i1,i2,…,it),即满足pk=cik。其中,k=1,2,…,t;1≤i1 定义2带重要点约束的最长公共子轨迹(Constrained Longest Common Subtrajectory,CLCS) 令ε>0为距离阈值,设经典轨迹Cm与实时轨迹Qn在重要点Pt=(p1,p2,…,pt)约束下的公共子轨迹为Zr=(z1,z2,…,zr),则Zr必须满足 (4) 式中:dis(ciw,qjw)为ciw与qjw两点之间的欧氏距离,dis(ciw,pw)为ciw与pw两点之间的欧氏距离,dis(qjw,pw)为两点qjw与pw之间的欧氏距离。 Zr为两轨迹Cm与Qn在重要点Pt=(p1,p2,…,pt)约束下的CLCS,当且仅当Zr为满足式(4)的LCS。 令ε>0为距离阈值,L2ε(m,n,t)为经典轨迹Cm与实时轨迹Qn在重要点Pt=(p1,p2,…,pt)约束下的CLCS长度,根据CLCS定义,有如式(5)所示的CLCS长度计算的递推公式L2ε(i,j,k): (5) 式中:dis(ci,qj)为ci与qj两点之间的欧氏距离,dis(ci,pk)为ci与pk两点之间的欧氏距离。计算L2的初始值为 L2ε(i,j,k)=-∞,k>0 , (6) (7) 令L2ε(m,n,t)为经典轨迹Cm与实时轨迹Qn在重要点Pt=(p1,p2,…,pt)约束下的CLCS的长度,定义Cm与Qn在重要点Pt=(p1,p2,…,pt)约束下的受限轨迹相似度为 (8) 上述公式为基于CLCS的带重要点约束的经典轨迹相似度量基础算法,简称CLCS算法。f2ε(Cm,Qn,Pt)计算的时空复杂度为O(mnt)。 定义3带匹配路径约束的最长公共子轨迹(Matching Path Constrained Longest Common Subtrajectory,MPCLCS) 令ε>0为距离阈值,设经典轨迹Cm与实时轨迹Qn及Cm中指定重要点位置序列It=(i1,i2,…,it)约束下的公共子轨迹为Zr=(z1,z2,…,zr),则Zr必须满足 (9) 式中:dis(ciw,qjw)为ciw与qjw两点之间的欧氏距离。 Zr为两轨迹Cm与Qn在重要点匹配路径It=(i1,i2,…,it)约束下的MPCLCS,当且仅当Zr为满足式(9)的LCS。 令ε>0为距离阈值,L3ε(m,n,t)为经典轨迹Cm与实时轨迹Qn在匹配路径It=(i1,i2,…,it)约束下的MPCLCS长度,根据MPCLCS定义,有如式(10)所示的MPCLCS长度计算的递推公式L3ε(i,j,t): (10) 式中:dis(ci,qj)为ci与qj两点之间的欧氏距离。计算L3的初始值为 (11) 式中:i1表示It中的第一个元素,i=0,1,2,…,m;j=0,1,…,n。 令L3ε(m,n,t)为经典轨迹Cm与实时轨迹Qn在匹配路径It=(i1,i2,…,it)约束下的MPCLCS的长度,定义Cm与Qn在匹配路径It=(i1,i2,…,it)约束下的受限轨迹相似度为 (12) 上述公式为基于MPCLCS的带重要点约束的经典轨迹相似度量快速算法(带匹配路径约束的经典轨迹相似度量算法),简称MPCLCS算法。f3ε(Cm,Qn,It)计算的时空复杂度为O(mn)。 令ε>0为距离阈值,经典轨迹为Cm,实时轨迹为Qn,Cm中指定重要点位置序列It=(i1,i2,…,it),重要点位置序列对应的重要点Pt=(p1,p2,…,pt),设f1ε(Cm,Qn),f2ε(Cm,Qn,Pt),f3ε(Cm,Qn,It)分别为LCS算法的轨迹相似度、CLCS算法的轨迹相似度、MPCLCS算法的轨迹相似度,则有如下性质成立: 性质1f3ε(Cm,Qn,It)≤f2ε(Cm,Qn,Pt)≤f1ε(Cm,Qn)。 性质2 当ε→∞时,有f3ε(Cm,Qn,It)=f2ε(Cm,Qn,Pt)=f1ε(Cm,Qn)=min{m,n}/m。 性质3 当Qn=Cm时,有f3ε(Cm,Qn,It)=f2ε(Cm,Qn,Pt)=f1ε(Cm,Qn)=1。 因篇幅所限,上述性质证明略。 为了验证新算法的有效性,根据实际数据,在指定重要点时选取不同距离门限对比LCS算法、CLCS算法、MPCLCS算法的相似度和计算时间,实验结果在算法距离门限实验中描述。在算法重要点实验中,指定距离门限选取不同数量的重要点个数对比LCS、CLCS、MPCLCS算法的相似度和计算时间。在噪声干扰实验中,指定距离门限和指定重要点,增加噪声干扰,对比LCS、CLCS、MPCLCS算法的相似度和计算时间。三个实验所涉及的实验环境:Matlab7软件;Windows7系统;联想电脑M660(处理器为Intel©CoreTMi5-6500 CPU @3.20 GHz 3.20 GHz)。 实验数据为6个空中目标不同时间段的飞行数据,经过挖掘后形成的6条经典轨迹和最后一次接收的6条实时轨迹,轨迹是按时间从小到大排列而成的有序的二维位置点。将6条经典轨迹进行等间隔抽取5%的轨迹点为重要点,即从第1点开始每20个点抽取第1个点作为重要点,将重要点在经典轨迹中的位置作为MPCLCS算法的重要点约束,将重要点组成的轨迹作为CLCS算法的重要点约束轨迹。6条经典轨迹的长度分别为107、177、125、145、107、118,6条实时轨迹长度分别为156、160、126、149、114、145。MPCLCS算法和CLCS算法中涉及的6条重要点约束轨迹的长度相同,对应的位置相同。6条经典轨迹对应的6条重要点约束轨迹的长度分别为6、9、7、8、6、6。6个目标的经典轨迹及对应的重要点约束轨迹和实时轨迹如图1所示。 图1 轨迹位置 为了比较不同距离门限下各算法的相似度和计算时间,将距离门限从5 km开始逐步递增到30 km。经统计,各算法相似度和计算时间如图2和图3所示。 图2 不同距离门限的相似度量 图3 不同阈值的计算时间 在图2(a)~(f)中,距离门限变动时,MPCLCS算法和CLCS算法计算的相似度相同,这说明MPCLCS新算法相似度性能与CLCS算法一致。当距离门限较大(如距离门限为30 km)时,三种算法相似度都较大且相同,这说明了MPCLCS算法和CLCS算法在满足重要点约束要求时,相似度能够达到LCS算法的相似度,且增加约束后相似度没有受影响。当距离门限较小(如在图2(b)~(f)中距离门限为5 km)时,带重要点约束的算法MPCLCS和CLCS的相似度都为0,而没有带重要点约束的LCS算法的相似度较大,这说明算法MPCLCS和CLCS中的重要点对相似轨迹进行了有效的约束。 从图2(a)~(f)看出,只有图2(e)和图2(f)表示的目标5和目标6的MPCLCS算法和CLCS算法相似度有细微差距。经过计算,目标5的相似度在距离门限小于等于15 km时,MPCLCS算法和CLCS算法的相似度都为0。这是由于目标5中最后一个重要点与实时轨迹中所有点距离都超过15 km,因此不能满足重要点约束要求,这与实验结果一致,故算法MPCLCS和CLCS对重要点约束是有效的。MPCLCS算法和CLCS算法相似度之差不超过1.7%,但MPCLCS算法的计算时间比CLCS算法的计算时间少30%以上,MPCLCS算法最多比LCS算法的计算时间多4.2%。这说明MPCLCS算法是比CLCS算法计算速度更快的相似度量算法,其计算时间与LCS算法一致。 在图3(a)~(f)中,随着距离门限不断增加,CLCS算法运行时间不断增加,MPCLCS算法的运行时间与LCS算法运行时间变化不大,且MPCLCS算法的运行时间与LCS算法运行时间接近。这说明CLCS算法运行时间受距离门限的影响较大,MPCLCS算法运行时间几乎没有影响。 综上,选取不同距离门限时,MPCLCS算法始终和CLCS算法相似度一致,计算时间与LCS算法一致。 为了比较不同重要点数量各算法的相似度和计算时间,实验数据仍为图1中的6个空中目标,但固定距离门限,变动重要点约束条件。将经典轨迹等间隔选取轨迹点作为重要点,设经典轨迹的重要点率p=1/k,k为正整数,k表示经典轨迹中每k个点选取第一点为重要点,将重要点在经典轨迹中的位置作为MPCLCS算法的重要点约束,将重要点组成的轨迹作为CLCS算法的重要点约束轨迹。令距离门限ε=30 km,重要点率从5%逐步递增到20%,经统计,各算法相似度和计算时间如图4和图5所示。 图4 不同重要点数量的相似度量 图5 不同重要点数量的计算时间 在图4中,在不同重要点数量约束下,MPCLCS算法计算相似度始终和CLCS算法一致;在满足重要点约束要求时,MPCLCS算法和CLCS算法计算相似度都与LCS算法一致。这说明MPCLCS算法和CLCS算法在满足重要点约束要求时,重要点约束对MPCLCS算法和CLCS算法的相似度无影响,相似度可以达到LCS算法的相似度。 从图4(a)~(f)看出,只有图4(f)表示的目标6的MPCLCS算法和CLCS算法相似度有细微差距。经过计算,重要点率从5%逐步递增到50%时,MPCLCS算法与CLCS算法的相似度之差小于8%,MPCLCS算法的计算时间比CLCS算法的计算时间少57%以上,MPCLCS算法最多比LCS算的计算时间多4.2%。 在图5(a)~(f)中,随着重要点数不断增加,CLCS算法运行时间不断增加,MPCLCS算法的运行时间与LCS算法运行时间变化不大,且MPCLCS算法的运行时间与LCS算法运行时间接近。这说明了CLCS算法运行时间受重要点个数的影响较大,MPCLCS算法运行时间几乎没有影响。 综上,经典轨迹中选取不同的重要点约束条件时,MPCLCS算法始终和CLCS算法相似度一致,计算时间与LCS算法一致。 在图6中,在不同扰动数量约束下,MPCLCS算法计算相似度始终和CLCS算法一致;在满足重要点约束要求时,MPCLCS算法和CLCS算法计算相似度都与LCS算法一致。这说明MPCLCS算法和CLCS算法在满足重要点约束要求时,实时轨迹中增加噪声干扰对MPCLCS算法和CLCS算法的相似度无影响,相似度可以达到LCS算法的相似度。 从图6(a)~(f)看出,只有图6(f)表示的目标6的MPCLCS算法和CLCS算法相似度有细微差距。经过计算,扰动率从5%逐步递增到50%时,MPCLCS算法与CLCS算法的相似度之差小于4%,MPCLCS算法的计算时间比CLCS算法的计算时间少53%以上,MPCLCS算法最多比LCS算法的计算时间多1.3%。 图6 不同扰动数量的相似度量 在图7中,在不同扰动数量约束下,MPCLCS算法计算时间始终和LCS算法一致,CLCS算法的计算时间比LCS算法计算时间大1倍以上。这说明不同噪声干扰条件下,MPCLCS算法计算时间始终和LCS算法一致。 图7 不同扰动数量的计算时间 综上,实时轨迹中增加不同的轨迹点干扰数量时,MPCLCS算法始终和CLCS算法相似度一致,计算时间与LCS算法计算时间一致。 针对轨迹中包含特殊语义的重要点,本文提出了一种带重要点约束的轨迹相似度量模型,并根据该模型提出了两种相似度量算法,一种时空复杂度为O(mnt)的带重要点约束的经典轨迹相似度量基础算法(CLCS算法)和一种时空复杂度为O(mn)的带重要点匹配路径约束的经典轨迹相似度量快速算法(MPCLCS算法)。CLCS算法要求重要点是相似轨迹和经典轨迹的子轨迹;MPCLCS算法除了要求重要点是相似轨迹和经典轨迹的子轨迹之外,还要求重要点是经典轨迹中的点。MPCLCS算法计算的相似度能够接近CLCS算法计算的相似度,计算时间又与没有重要点约束的LCS算法一致。同LCS算法相比,MPCLCS算法在不增加计算量的同时实现了对重要点约束的要求。 MPCLCS算法简单快速,易于工程实现,能够为实时目标识别与轨迹预测提供包含重要点或重要语义的相似轨迹判断算法,具有重要的工程应用价值。 MPCLCS算法主要采用的是点与点之间的欧氏距离,其计算简单,但未考虑到经典轨迹与实时轨迹之间的大差异性。下一步将研究如何在大差异数据下提高算法的鲁棒性,让算法能够适应这种大差异性。2.1 带重要点约束的经典轨迹相似度量基础算法
2.2 带重要点约束的经典轨迹相似度量快速算法
2.3 算法性质
3 实验
3.1 算法距离门限实验
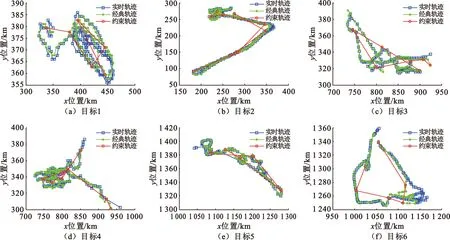
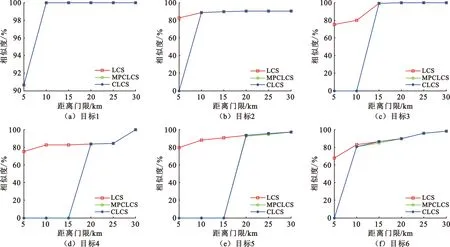
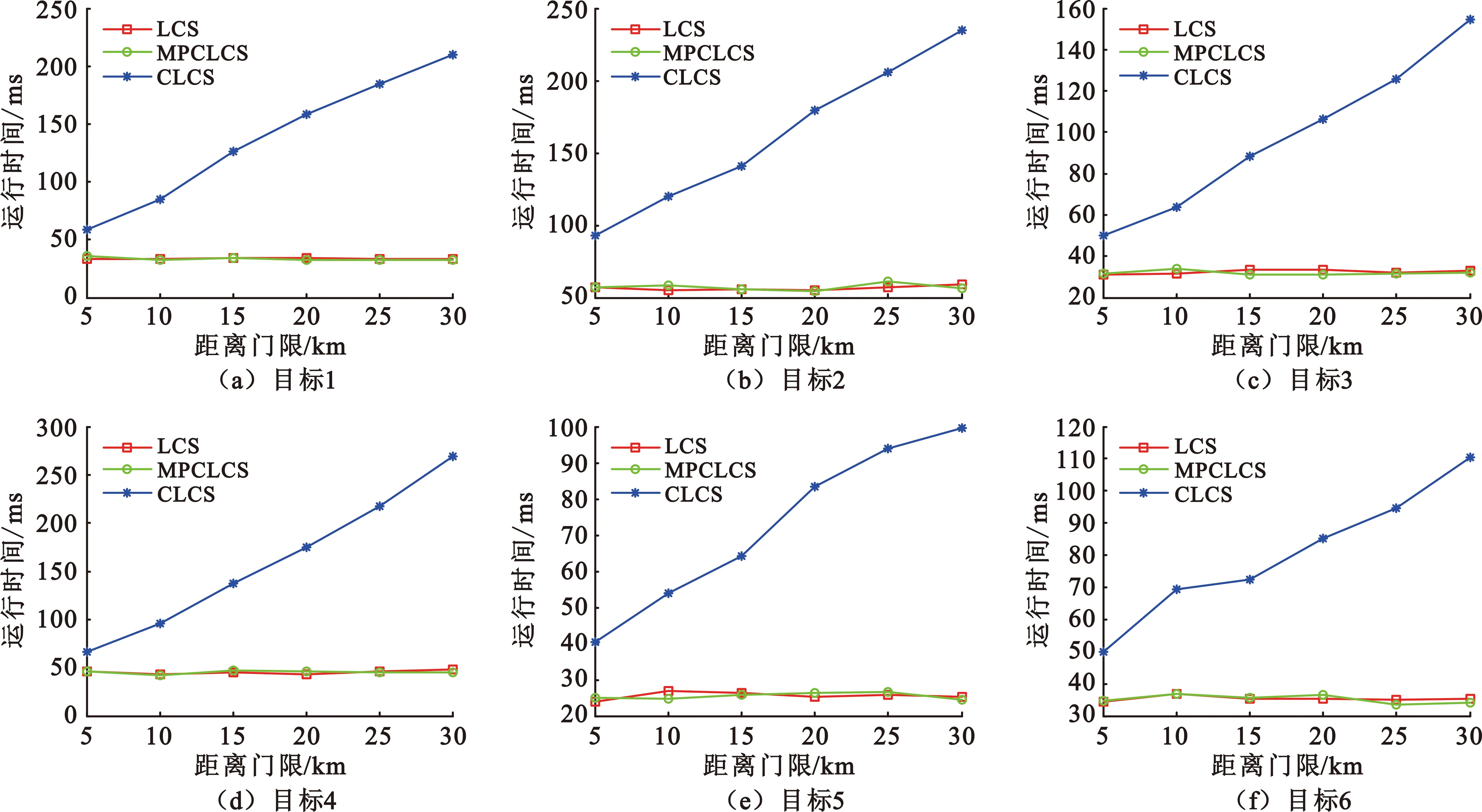
3.2 算法重要点实验
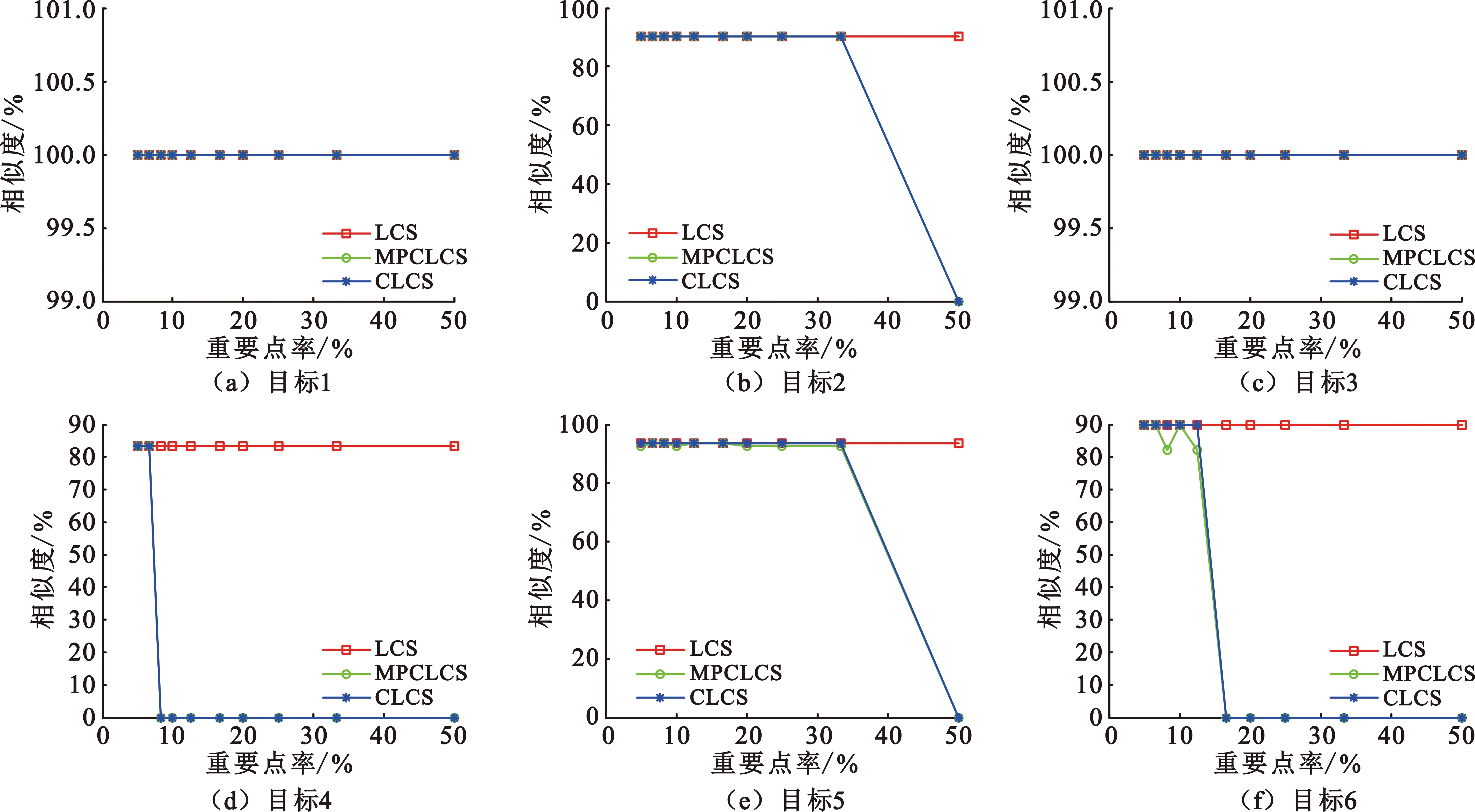
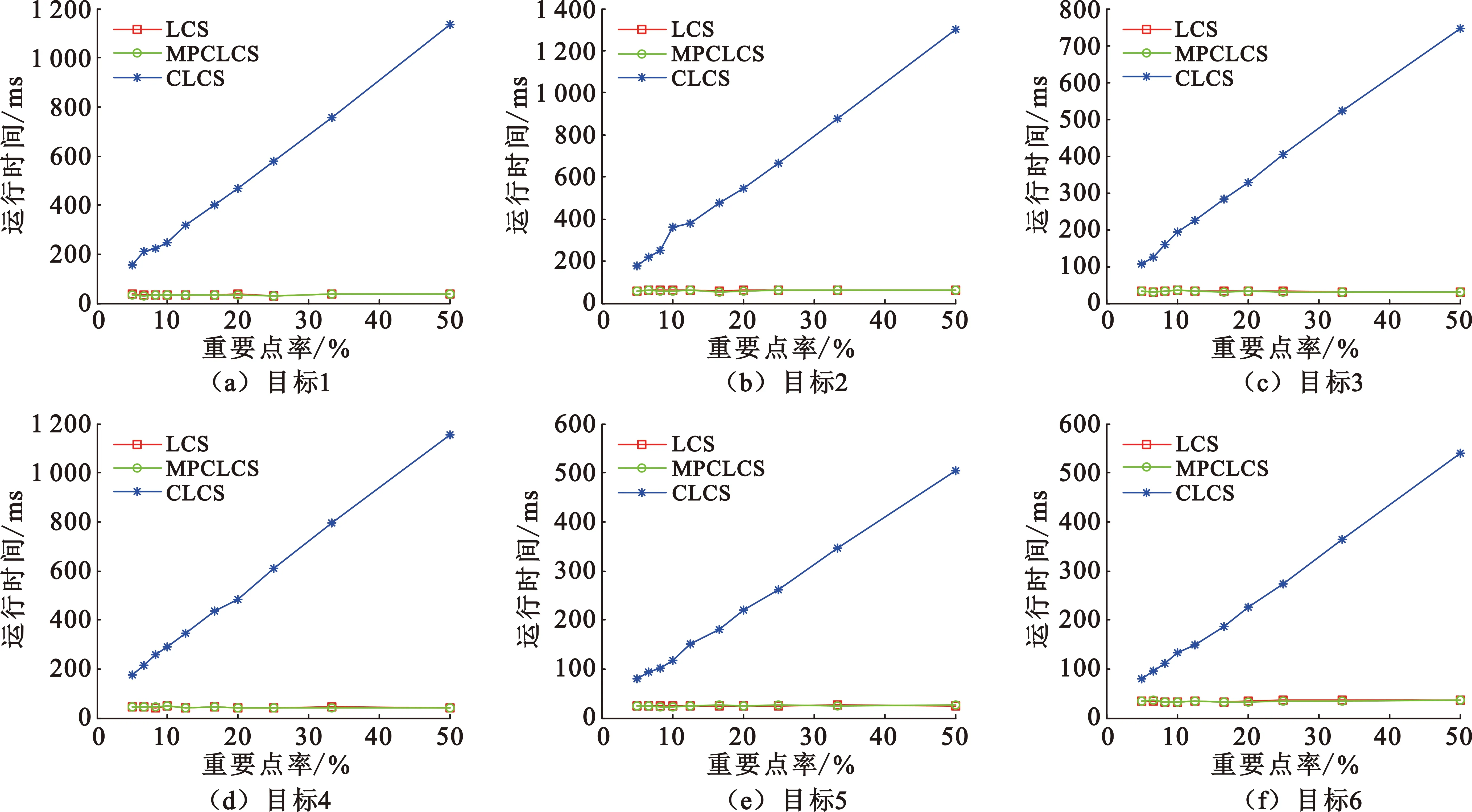
3.3 算法噪声干扰实验
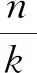

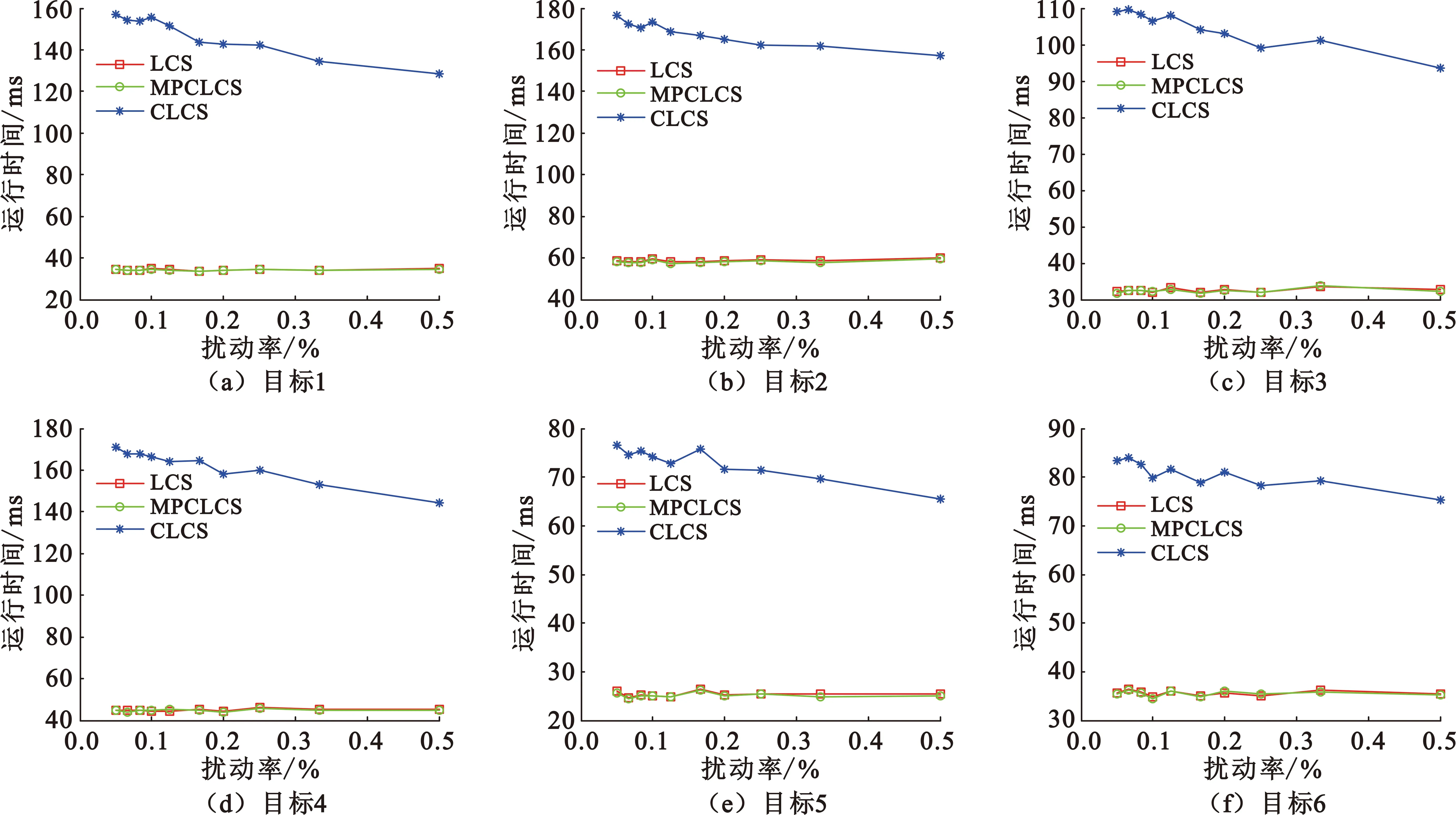
4 结束语

